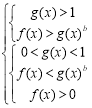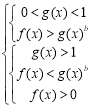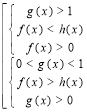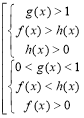Розв'язування нерівностей
Навчально-методичний посібник з розв'язування нерівностей для самостійної роботи студентів з метою навчитися розпізнавати і розв'язувати найпростіші види нерівностей та методи їх розв'язування, а також: показникових, логарифмічних, тригонометричних нерівностей.
Міністерство освіти і науки України
Львівський техніко-економічний коледж
НУ «Львівська політехніка»
Навчально-методичний посібник
показникових, логарифмічних,
тригонометричних
Львів – 2011
Розглянуто і схвалено
на засіданні циклової комісії
природничо-математичних
дисциплін
Протокол №___ від ___________ 2011 р.
Голова комісії Давидова О.В.
Навчально-методичний посібник (запитання, відповіді, зразки розв’язування, вправи для закріплення). Розв’язування нерівностей:
показникових, логарифмічних, тригонометричних
Сулик Н.Я., - Львів, ЛТЕКНУЛП, 2011 р.
Рецензент: Федочинська С.С.
Передмова
Рівняння, нерівності і системи рівнянь та нерівностей є математичними моделями багатьох фізичних та інших явищ. Тому розв’язування різних практичних задач зводиться до розв’язування рівнянь, нерівностей та їхніх систем.
Даний посібник є логічним продовженням розкриття розділу «Рівняння, нерівності та їхні системи».
Навчальна мета посібника – допомогти студентам навчитися розпізнавати і розв’язувати найпростіші види нерівностей та методи їх розв’язування, а також основні методи розв’язування показникових, логарифмічних та тригонометричних нерівностей.
Для цього тут зібрана достатньо повна інформація про види нерівностей і способи їх розв’язування для різного роду нерівностей одного типу.
Використовуючи наданий у посібнику матеріал студент має змогу повторити принципи розв’язування лінійних нерівностей, метод інтервалів для розв’язування нерівностей. Важливе місце займають завдання, спрямовані на формування навичок студентів у розпізнаванні лінійних та квадратичних нерівностей, в яких невідомою величиною є трансцендентна функція (показникова, логарифмічна, тригонометрична тощо).
У посібнику наведено приклади розв’язування нерівностей, які студент повинен вміти розв`язувати самостійно.
Для перевірки засвоєних знань підібрано нерівності для самостійного розв’язування та відповіді до них, які студент повинен навчитися розв`язувати, використовуючи навчальний матеріал посібника.
Якщо розв’язування цих завдань викликає труднощі, тоді слід ще раз повернутися до розгляду розв’язаних аналогічних прикладів, що містяться в посібнику.
Зібрані у посібнику завдання відповідають вимогам чинної програми з математики та вимагають мінімального рівня засвоєння курсу математики по розділах “Числа. Арифметичні дії.”, “Вирази. Основні поняття і види”, “Функції та їхні властивості”.
1. Нерівності. Основні поняття.
Дві функції, що поєднані між собою знаком понерівність утворюють нерівність: f(x)>g(x); f(x)≥g(x); f(x)<g(x); f(x)≤g(x).
Розв’язком нерівності називається значення х, яке задовольняє їх.
Розв’язати нерівність – означає знайти множину усіх її розв’язків або встановити, що нерівність розв’язків не має.
Областю визначення D нерівності називають множину всіх значень невідомої, на якій існують функції f(x), g(x). При визначенні D часто вводяться також додаткові умови, які пов’язані з характером нерівності.
Наприклад, для нерівності ![]() область визначення D знаходиться таким чином:
область визначення D знаходиться таким чином: ![]() . Тут враховано, що ліва частина нерівності, яка за умовою не менша
. Тут враховано, що ліва частина нерівності, яка за умовою не менша ![]() , не може бути від’ємною.
, не може бути від’ємною.
Якщо Ви бажаєте навчитися розв’язувати нерівність, тоді спочатку треба вивчити досконало відповіді на наступні запитання:
- Що таке нерівність?
- Що називається областю визначення нерівності?
- Що називається розв’язком нерівності?
- Що означає розв’язати нерівність?
- Від чого залежить назва нерівності?
- Які нерівності називаються еквівалентними?
- Які перетворення можна виконувати над нерівностями?
- Яка нерівність називається лінійною?
- Яка нерівність називається квадратичною?
- Яка нерівність називається дробово-раціональною?
- Яка нерівність називається ірраціональною?
- Яка нерівність називається показниковою?
- Яка нерівність називається логарифмічною?
- Яка нерівність називається тригонометричною?
Це треба знати
- Що таке нерівність?
Нерівністю називається вираз, у якому будь-які дві функції поєднані знаком понерівність f(x)>g(x); f(x)≥g(x); f(x)<g(x); f(x)≤g(x).
- Що називається областю визначення нерівності?
Областю визначення D нерівності називають множину всіх значень невідомої змінної х, на якій існують функції f(x), g(x). Тобто це спільна область визначення функцій f(x) i g(x).
- Що називається розв’язком нерівності?
Значення змінної х, при яких нерівність виконується називається розв’язком нерівності. Сукупність (об’єднання) усіх розв’язків нерівності називається множиною її розв’язків, тобто множиною розв’язків нерівності.
- Що означає розв’язати нерівність?
Розв’язати нерівність означає знайти сукупність усіх розв’язків цієї нерівності або довести, що вони не існують.
- Від чого залежить назва нерівності?
Назву нерівності визначає характер функцій f(x) i g(x), з яких складається ця нерівність: дробово-раціональна, ірраціональна, показникова, логарифмічна і тригонометрична тощо.
- Які нерівності називаються еквівалентними?
Дві нерівності називаються еквівалентними, якщо множини всіх розв’язків цих нерівностей співпадають.
Нерівність еквівалентна сукупності нерівностей, якщо множина її розв’язків співпадає з об’єднанням множин усіх розв’язків нерівностей, що входять у цю сукупність.
Під множиною розв’язків системи нерівностей розуміють перетин множин розв’язків усіх нерівностей, що входять у цю систему.
Нерівність називають еквівалентною системі нерівностей, якщо множина її розв’язків співпадає з множиною розв’язків цієї системи.
У математиці існують правила, які дозволяють перетворювати задану нерівність у рівносильну до неї.
- Які перетворення можна виконувати над нерівностями?
- Якщо функція f(x) тотожно рівна функції f1(x) i функція g(x) тотожно рівна функції g1(x), тоді нерівність f1(x)=g1(x) рівносильна нерівності f(x)>g(x).
- Якщо до обох частин нерівності додати (або відняти) один і той самий вираз, що має зміст в області визначення заданої нерівності, тоді отримаємо рівносильну нерівність до заданої: f(x)±с(х)>g(x)±с(х).
- Якщо обидві частини нерівності помножити (або поділити) на один і той самий вираз, що має зміст в області визначення заданої нерівності і не дорівнює в цій області нулю, тоді отримаємо рівносильну нерівність до заданої при умові, що с(х)>0: f(x)*с(х)>g(x)*с(х) чи f(x)/с(х)>g(x)/с(х), с(х)≠0 або при умові, що с(х)<0: f(x)*с(х)<g(x)*с(х) чи f(x)/с(х)<g(x)/с(х), с(х)≠0.
Зверніть увагу, що при множенні (діленні) нерівності на від’ємний вираз знак нерівності міняється на протилежний.
- Якщо ж вираз в області визначення дорівнює нулю с(х)=0,тоді при множенні на нього обох частин нерівності, отримана нерівність буде наслідком даної, а при діленні навпаки, дана нерівність буде наслідком отриманої. (Аналогічно до рівнянь.) Це означає , що при множенні можна отримати сторонні розв’язки нерівності, а при діленні – втратити деякі з них.
- Якщо ліва частина нерівності є добутком кількох виразів, а права нуль, тоді сукупність нерівностей, ліва частина яких є множниками добутку, а права нуль, є наслідком даної нерівності. Тут варто застосувати метод інтервалів. (Див. далі).
- Якщо обидві частини нерівності піднести до одного і того самого степеня, тоді отримаємо наслідок до даної нерівності: fп(x)>gп(x). Якщо при піднесенні до степеня обидві частини нерівності зберігають в області його визначення невід’ємне значення, тоді отримана нерівність буде рівносильною до даної.
- Яка нерівність називається лінійною?
Нерівність виду ах+b>с, де а≠0 називається лінійною.
Розв’язком лінійної нерівності є значення змінної х![]()
![]() , якщо а>0 або х
, якщо а>0 або х![]()
![]() , якщо а<0.
, якщо а<0.
- Яка нерівність називається квадратичною?
Нерівність виду ах2+bх+с>0, де а≠0 називається квадратичною.
Для розв’язування квадратичної нерівності використовується метод інтервалів:
значеннями х =![]() , де D=b2-4ac, розбиваємо числову вісь на інтервали і вибираємо потрібні, визначаючи знак нерівності на кожному з них за правилом:
, де D=b2-4ac, розбиваємо числову вісь на інтервали і вибираємо потрібні, визначаючи знак нерівності на кожному з них за правилом:
![]()
![]() , якщо а>0 або , якщо а<0.
, якщо а>0 або , якщо а<0.
х1 х2 х1 х2
Тоді у першому випадку розв’язки нерівності матимуть ![]() , а у другому
, а у другому ![]() .
.
- Яка нерівність називається дробово-раціональною?
Загальний вид дробово-раціональної нерівності можна записати ![]() , де Рп(х),Qm(x) – многочлени п-го і т-го порядку відповідно: Рп(х)=а0хп+а1хп-1+а2хп-2+…+ап-1х+ап, а0≠0; Qm(х)=b0хm+b1хm-1+b2хm-2+…+bm-1х+bm, b0≠0.
, де Рп(х),Qm(x) – многочлени п-го і т-го порядку відповідно: Рп(х)=а0хп+а1хп-1+а2хп-2+…+ап-1х+ап, а0≠0; Qm(х)=b0хm+b1хm-1+b2хm-2+…+bm-1х+bm, b0≠0.
Нерівності такого виду розв’язуються методом інтервалів (Див.далі.)
Багато нерівностей зводяться до заданих за допомогою різних перетворень. (Способи перетворень розглянемо пізніше.)
- Яка нерівність називається ірраціональною?
Нерівність, у якій змінна х міститься під знаком радикала (![]() ) або підноситься до дробового показника степеня, називається ірраціональною.
) або підноситься до дробового показника степеня, називається ірраціональною.
Загальний вид найпростішої ірраціональної нерівності ![]() >с. Розв’язком нерівності є значення змінної х
>с. Розв’язком нерівності є значення змінної х![]() (c2; +∞).
(c2; +∞).
- Яка нерівність називається показниковою?
Нерівність, в якій змінна х міститься в показнику степеня, називається показниковою: ах>b, b>0. Розв’язком нерівності є значення змінної х![]() (logab;+∞), якщо а>1 або х
(logab;+∞), якщо а>1 або х![]() (–∞;logab), якщо 0<а<1.
(–∞;logab), якщо 0<а<1.
- Яка нерівність називається логарифмічною?
Нерівність, в якій змінна х міститься під знаком логарифмічної функції, називається логарифмічною: logax>b. Розв’язком нерівність є значення змінної х![]() (ab;+∞), якщо а>1 або х
(ab;+∞), якщо а>1 або х![]() (0;ab), якщо 0<а<1.
(0;ab), якщо 0<а<1.
- Яка нерівність називається тригонометричною?
Нерівність, в якій змінна х міститься під знаком тригонометричної функції, називається тригонометричною. Наприклад, sin x>a, cos x<a, tg x≤a, ctg x≥a. Розв’язки таких нерівностей розглянемо пізніше.
2. Вчимося розв’язувати нерівності.
Розв’язування нерівностей, як правило, зводиться до розв’язування сукупності або системи нерівностей.
Розв’язати сукупність нерівностей означає знайти об’єднання розв’язків кожної з нерівностей, що входять у сукупність.
Розв’язати систему нерівностей означає знайти перетин розв’язків нерівностей, з яких вона складається.
Для перетворення заданих нерівностей до більш простих чи відомих діємо наступним чином:
1) знаходиться область визначення нерівності;
2) шляхом різних перетворень задана нерівність зводиться до нерівності, розв’язки якої можна знайти за відомими формулами або за відомим алгоритмом, далі знаходяться розв’язки перетвореної нерівності;
3) перевіряється належність знайдених розв’язків до області визначення нерівності і визначається загальний розв’язок з отриманої сукупності чи системи розв’язків.
У деяких випадках недоцільно знаходити область визначення нерівності, яка розв’язується, оскільки перевірка знайдених значень невідомого за умовою заданої нерівності є складовою частиною розв’язування нерівності. Але ця властивість визначається безпосередньо характером заданої нерівності.
Перед знаходженням розв’язків задану нерівність перетворюють до більш простого вигляду, розв’язки якої можна знайти за відомими формулами або шляхом послідовного виконання простих операцій (розкладання на множники та ін.).
Усі нерівності так як і рівняння діляться на дві великі групи: алгебраїчні та функціональні нерівності.
В алгебраїчних нерівностях змінна може позначатися будь-якою латинською буквою, найчастіше це х, t, u, y, a, b …
У функціональних нерівностях невідома міститься під знаком трансцендентної функції, як правило цю функцію позначають новою змінною і розв’язування зводиться до розв’язування вже відомих алгебраїчних нерівностей, зокрема, найпростіших.
Оскільки безмежна кількість нерівностей зводиться до розв’язування найпростіших нерівностей: лінійних, квадратичних, почнемо вивчення розв’язування нерівностей саме з них.
Умовні позначення числових проміжків
|
назва |
позначення |
зображення |
запис у вигляді нерівності |
|
числова пряма |
(–∞;+∞) або R |
|
–∞<x<+∞ |
|
відрізок |
[a;b] |
|
a≤x≤b |
|
інтервал |
(a;b) |
|
a<x<b |
|
пів інтервал |
[a;b) |
|
a≤x<b |
|
(a;b] |
|
a<x≤b |
|
|
промінь |
(–∞;a) |
|
–∞<x<a |
|
(–∞;a] |
|
–∞<x≤a |
|
|
(a;+∞) |
|
a<x<+∞ |
|
|
[a;+∞) |
|
a≤x<+∞ |
Як вам уже відомо нерівність виду ах+b>с або ах+b<с (ах+b≥с або ах+b≤с), де а≠0 називається лінійною. Тут a,b,c – довільні числа, х – невідома.
Розглянемо різноманітні випадки розв’язування лінійних нерівностей. (тут a,b,c – довільні додатні числа)
|
Нерівність |
Розв’язок нерівності |
|
x + b > 0 або b + x > 0 |
x > – b |
|
x + b > c або b + x > c |
x > c – b |
|
x + b > –c або b + x > –c |
x > – c – b |
|
x – b > 0 |
x > b |
|
x – b > с |
x > c + b |
|
x – b > –c |
x > b – c |
|
b – x > 0 |
x < b |
|
b – x > c |
x < b – c |
|
b – x > –c |
x < c + b |
|
ax > 0 |
x > 0 |
|
–ax > 0 |
x < 0 |
|
ax > c |
x > c / a |
|
–ax > –c |
x < c / a |
|
ax > –c |
x > – c / a |
|
–ax > c |
x < – c / a |
|
ax + b > 0 |
x > – b / a |
|
–ax – b > 0 |
x < – b / a |
|
ax – b > 0 |
x > b / a |
|
–ax + b > 0 |
x < b / a |
|
ax + b > c |
х > |
|
–ax – b>–c |
х < |
|
ax – b > c |
х > |
|
–ax + b>–c |
х < |
|
ax + b >–c |
х > |
|
–ax – b>c |
х < |
|
ax – b >–c |
х > |
|
–ax + b>c |
х < |
Приклади розв’язування лінійних нерівностей:
-
х + 3 > 5
 х > 5 – 3
х > 5 – 3  х > 2.
х > 2.
-
х – 3 > 5
 х > 5 + 3
х > 5 + 3  х > 8.
х > 8.
-
3 + х > 5
 х > 5 – 3
х > 5 – 3  х > 2.
х > 2.
-
3 – х > 5
 3 – 5 > x
3 – 5 > x  х < –2.
х < –2.
-
–х + 3 > 5
 –х > 5 – 3
–х > 5 – 3  –х > 2
–х > 2  x < –2.
x < –2.
-
–х – 3 > 5
 –х > 5 + 3
–х > 5 + 3  –х > 8
–х > 8  х < –8.
х < –8.
-
х + 3 < 0
 х < 0 – 3
х < 0 – 3  х < –3.
х < –3.
-
х – 3 > 0
 х > 0 + 3
х > 0 + 3  х > 3.
х > 3.
-
–х + 3 < 0
 –х < 0 – 3
–х < 0 – 3  –х < –3
–х < –3  х > 3.
х > 3.
-
2х > 0
 х > 0/2
х > 0/2  х > 0.
х > 0.
-
2х < 6
 х < 6/2
х < 6/2  х < 3.
х < 3.
-
2х > 7
 х > 7/2
х > 7/2  х > 3,5.
х > 3,5.
-
2х + 4 > 0
 х > (0–4)/2
х > (0–4)/2  х > –2.
х > –2.
-
2х – 4 < 0
 х < (0+4)/2
х < (0+4)/2  х < 4/2
х < 4/2  х < 2.
х < 2.
-
3х + 6 < 15
 х < (15–6)/3
х < (15–6)/3  х < 9/3
х < 9/3  х < 3.
х < 3.
-
6 – 4х ≥ 2
 – 4х ≥ 2 – 6
– 4х ≥ 2 – 6  х ≤ (–4)/(–4)
х ≤ (–4)/(–4)  х ≤ 1.
х ≤ 1.
Приклади розв’язування нерівностей, що зводяться до лінійних:
-
х + 3 > х + 5
 х – х > 5–3
х – х > 5–3  0 > 2
0 > 2  розв’язків не має.
розв’язків не має.
-
х + 3 < 5 − х
 х + х < 5−3
х + х < 5−3  2х < 2
2х < 2  х < 2/2
х < 2/2  х<1.
х<1.
-
3х + 2 ≥ 5 − 4x
 3х + 4x ≥ 5 – 2
3х + 4x ≥ 5 – 2  7x ≥ 3
7x ≥ 3  x ≥ 3/7.
x ≥ 3/7.
-
3(х + 6) − 2х < 4х − 3
 3х + 18 −2х − 4х < −3
3х + 18 −2х − 4х < −3 
![]() − 3х < −3 −18
− 3х < −3 −18 ![]() −3х < −21
−3х < −21 ![]() х > 7.
х > 7.
Розв’яжіть самостійно:
- 3х – 5 > 7
- 2 + х < – 4
- 16 – х ≤ 8
- 15 + 3х ≥7 − 2(х − 5)
- 37 + 5х ≥ 2(х − 3)
- 4х − 8 > −(5 + 6х) + 3
- 14 − 3х < х + 2(7 − 2х)
- 17 + 5х ≤ 3х − (6 − 2х)
Нерівність виду ах2+bх+с>0, де а≠0 називається квадратичною. Тут a,b,c – довільні числа, х – невідома.
Для її розв’язування необхідно обчислити дискримінант D=b2−4ac, за допомогою якого визначити корені відповідного квадратного рівняння: ![]() ,х1<х2.
,х1<х2.
Схема пошуку розв’язків для нерівності ах2+bх+с>0:
|
D>0 |
D=0, D<0 |
||
|
a>0 |
a<0 |
a>0 |
a<0 |
|
|
|
|
|
Схема пошуку розв’язків для нерівності ах2+bх+с<0:
|
D>0 |
D=0, D<0 |
||
|
a>0 |
a<0 |
a>0 |
a<0 |
|
|
|
|
|
Розглянемо різноманітні випадки розв’язування неповних квадратичних нерівностей, якщо а>0, b>0, c>0.
|
b=0 |
ах2+с>0 |
x2>–с/a |
|
|
ах2− с>0 |
x2>с/a |
|
|
|
с=0 |
ах2+bх>0 |
х (ах+b)>0 |
|
|
ах2−bх>0 |
х (ах−b)>0 |
|
|
|
b=с=0 |
ах2>0 |
х 2 >0 |
|
Розглянемо різноманітні випадки розв’язування неповних квадратичних нерівностей, якщо а<0, b>0.
|
b=0 |
ах2+с>0 |
x2<–с/a,c>0 |
|
|
ах2− с>0 |
x2<с/a,c<0 |
|
|
|
с=0 |
ах2+bх>0 |
х (ах+b)<0 |
|
|
ах2−bх>0 |
х (ах−b)<0 |
|
|
|
b=с=0 |
ах2>0 |
х 2 <0 |
|
Приклади розв’язування квадратичних нерівностей:
-
х2 + 3х − 4 > 0
 D = b2−4ac = 32−4∙1∙(−4) = 9+16 = 25
D = b2−4ac = 32−4∙1∙(−4) = 9+16 = 25
![]() ;
; ![]() .
.
![]() Розіб’ємо числову вісь знайденими коренями рівняння на проміжки і встановимо знак нерівності на кожному з них (див. пункт 1.9)
Розіб’ємо числову вісь знайденими коренями рівняння на проміжки і встановимо знак нерівності на кожному з них (див. пункт 1.9)
. Тоді, згідно умови запишемо результат:
–4 1 ![]() .
.
-
– х2 − 3х + 4 > 0
 D = (−3)2 − 4∙(–1)∙4 = 9+16 = 25
D = (−3)2 − 4∙(–1)∙4 = 9+16 = 25
![]() ;
; ![]() .
.
Розіб’ємо числову вісь знайденими коренями рівняння на проміжки і встановимо знак нерівності на кожному з них (див. пункт 1.9)
![]() . Тоді, згідно умови запишемо результат:
. Тоді, згідно умови запишемо результат:
–4 1 ![]() .
.
-
3х2 − х − 4 < 0
 D = b2−4ac = (−1)2−4∙3∙(−4) = 1+48 = 49
D = b2−4ac = (−1)2−4∙3∙(−4) = 1+48 = 49
![]() ;
; ![]() .
.
![]() Розіб’ємо числову вісь знайденими коренями рівняння на проміжки і встановимо знак нерівності на кожному з них (див. пункт 1.9)
Розіб’ємо числову вісь знайденими коренями рівняння на проміжки і встановимо знак нерівності на кожному з них (див. пункт 1.9)
–1 ![]() .
.
Тоді, згідно умови запишемо результат: ![]() .
.
-
4х2 − х + 3 < 0
 D = b2−4ac = (−1)2−4∙4∙3 = 1−48 =−47
D = b2−4ac = (−1)2−4∙4∙3 = 1−48 =−47
Оскільки D<0, a=4>0 розв’язком нерівності є ![]() .
.
-
х2 + 9 > 0
 х2 > –9
х2 > –9 
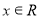 .
.
-
х2 − 9 > 0
 х2 > 9
х2 > 9  (х+3)(x–3) > 0
(х+3)(x–3) > 0 
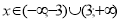 .
.
-
3х2 − 24 ≥ 0
 3х2 ≥ 24
3х2 ≥ 24  x2 ≥ 24∕3
x2 ≥ 24∕3 (х+2√2)(x–2√2) ≥ 0
(х+2√2)(x–2√2) ≥ 0 
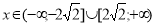 .
.
-
–3x2 – 6x ≥ 0
 –3x(х + 6) ≥ 0
–3x(х + 6) ≥ 0  х1 = 0; х2 =−6.
х1 = 0; х2 =−6.
![]() . Тоді,згідно умови запишемо результат:
. Тоді,згідно умови запишемо результат:
–6 0 ![]() .
.
-
18х − 9х2 ≤0
 9х(2 − х) ≤ 0
9х(2 − х) ≤ 0 х1 = 0; х2 = 2.
х1 = 0; х2 = 2.
![]() .Тоді,згідно умови запишемо результат:
.Тоді,згідно умови запишемо результат:
0 2 ![]() .
.
-
х2 − 14х + 49 > 0
 (х −7)2 > 0
(х −7)2 > 0 
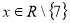 .
.
Приклад розв’язування біквадратичної нерівності:
-
х4 + 3х2 − 4 > 0. Введемо заміну змінних х2=t>0, отримаємо t2+3t−4>0
 D = 32−4∙1∙(−4) = 9+16 = 25
D = 32−4∙1∙(−4) = 9+16 = 25
![]() ;
; 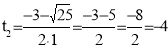
![]() . Тоді, згідно умови запишемо результат:
. Тоді, згідно умови запишемо результат:
–4 1 ![]() .
.
Повернімося до невідомої х: х2 <–4 ![]()
![]()
х2 >1 ![]()
![]()
Відповідь: ![]() .
.
Розв’яжіть самостійно:
- 2х2 + 5 > 7 5. 3х2 + 5х − 2 ≤ 0 9. 3х4 + 5х2 − 2 > 0
- 2 + х2 < 6 6. х2 − 8х + 16 ≥ 0 10.х4 − 8х2 + 12 ≤ 0
- 16 – х2 ≤ 0 7. −3х2 + х + 2 > 0 11.−3х4 + х2 + 2 ≥ 0
- 19 − 3х2 ≥7 8. х2 + 17х + 66 < 0 12.х4 + 17х2+ 66 < 0
Як правило, розв’язування раціональних нерівностей зводиться до використання методу інтервалів.
Для цього використовується принцип розкладання лівої частини нерівності на множники, якщо права частина рівна 0.
Як згадувалося раніше, цей метод використовується для розв’язування раціональних нерівностей виду: f(x)>g(x) або ![]() .
.
Метод інтервалів полягає у розкладанні на множники лівої частини нерівності і порівнянні її з нулем через визначення знаку нерівності на кожному з інтервалів, отриманих при розбитті числової прямої.
Існують різні схеми його використання, зокрема, у попередньому пункті було наведено приклади використання методу інтервалів для розв’язування квадратичних нерівностей.
Розглянемо загальний принцип використання методу інтервалів для розв’язування нерівності f(x)>g(x). У випадку нерівності f(x)<g(x) ця схема аналогічна.
Отже,
- Перенести всі члени заданої нерівності вліво: f(x)–g(x)>0.
-
Ліву частину отриманої нерівності привести до спільного знаменника:
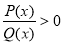 .
.
- Багаточлени P(x) та Q(x) розкласти на множники. Якщо при цьому з’являються однакові множники, треба замінити їх відповідними степенями. Наприклад,
![]() .
.
При скороченні треба пам’ятати, що
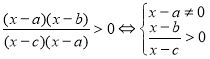 .
.
- Виключити з розкладання нелінійні множники.
Це виключення виконується за правилом:
- Якщо в розкладанні є множник ах2+bх+с, де b2-4ac<0, тоді його виключення залежить від знака старшого коефіцієнта а і виконується так:
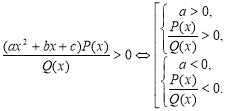
- Якщо в розкладанні є множник (х–а)2k, тоді його виключення виконується так:
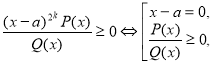
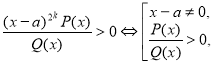
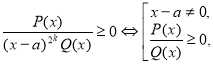
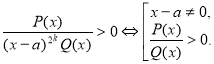
- Нелінійний множник (х–а)2k+1 виключається так:
![]()
- На числовій осі відмітимо точки, в яких перетворюються на нуль усі множники, що стоять у чисельнику і знаменнику лівої частини нерівності, отриманої після виконання пунктів 1-4.
При цьому слід звертати увагу на строгість чи нестрогість нерівності. Якщо нерівність строга, тоді усі точки «вирізуються» з числової осі, інакше, точки, які відповідають множникам у чисельнику треба «зафарбувати».
- Поставити знаки в кожному проміжку, на які числова вісь розбивається відміченими точками.
Спочатку поставити знак у найправішому проміжку на числовій осі за правилом:
«+» - якщо кількість множників виду (а–х) парна,
«–» - якщо кількість множників виду (а–х) непарна.
Знаки в інших проміжках ставляться з урахуванням черговості в сусідніх проміжках.
- Вибрати проміжки, в яких стоїть знак «+», якщо нерівність, отримана у пункті 4 має вигляд F(x)>0, або знак «–», якщо нерівність, отримана у пункті 4 має вигляд F(x)<0. Ці проміжки містять у собі крайні точки, відмічені на числовій осі зафарбованими і не містять «вирізані» точки.
Об’єднання таких проміжків і є множиною розв’язків даної нерівності.
Розглянемо приклади використання методу інтервалів:
- (х−3)2 + 3(х−3) − 4 > 0.
Введемо заміну змінних х−3=t ![]() t2+3t−4>0
t2+3t−4>0 ![]() D = 25:
D = 25: ![]() ;
; ![]()
Розкладемо на множники ліву частину заданої нерівності:
(t–1)(t+4)>0.
![]() Відмітимо на числовій осі точки .
Відмітимо на числовій осі точки .
–4 1
Тоді, запишемо результат: ![]() .
.
Знаки «+», «–» поставимо у відповідності з правилом 6.
Повернімося до невідомої х:
х − 3 < – 4 ![]() х<–1;
х<–1;
х − 3 > 1 ![]() х > 4.
х > 4.
Відповідь: ![]()
- 2х3 + 3х2 − 8х −12 <0.
Виконаємо перетворення лівої частини нерівності:
2х3+3х2−8х−12=х2(2х+3)−4(2х+3)=(х2−4)(2х+3).
Тоді нерівність матиме вигляд: (х−2)(х+2)(2х+3)<0.
Отримаємо три точки х1=2; х2=−2; х3=−1,5.
Відмітимо їх на числовій осі та розставимо знаки:
![]() .
.
–2 –1,5 2
Тоді, запишемо результат: ![]() .
.
Відповідь: ![]() .
.
Приведемо до спільного знаменника ліву частину нерівності: 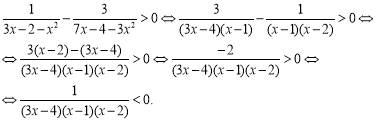
Ліва частина отриманої нерівності не має нелінійних множників.
Відмітимо на числовій осі точки х1=4/3; х2=1; х3=2 та розставимо знаки:
![]() .
.
1 4/3 2
Тоді, запишемо результат: ![]() .
.
Відповідь: ![]() .
.
Розкладемо чисельник і знаменник дробу, що стоїть у лівій частині нерівності, на множники:
![]()
Ліва частина отриманої нерівності містить нелінійні множники: (х2+2) та (х+1)2. Перший з них додатний і його можна опустити, другий множник виключимо у відповідності з пунктом 4 загальної схеми методу:
![]()
Відмітимо на числовій осі точки х1=2; х2=–2 та розставимо знаки:
![]() . Виберемо інтервал:
. Виберемо інтервал: ![]() .
.
–2 2
Нанесемо на числову вісь точку х=–1. Ця точка попадає у вибраний інтервал.
![]() .
.
–2 –1 2
«Виколюючи» точку х=–1, отримаємо результат:
![]() .
.
Відповідь: ![]() .
.
!!! Якщо точка на числовій осі входить до нерівності у парному показнику степеня, тоді знак нерівності на сусідніх інтервалах, утворених заданою точкою не змінюється.
Розв’яжіть самостійно:
-
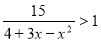 .
.
-
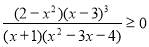 .
.
-
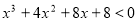 .
.
-
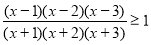 .
.
-
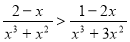
Нерівності, в яких невідоме міститься під знаком радикала, називають ірраціональними: ![]() .
.
Як правило, ірраціональні нерівності зводяться до еквівалентних систем раціональних нерівностей.
При розв’язуванні ірраціональної нерівності слід звертати особливу увагу на показник степеня радикала, а саме: парний чи не парний.
-
Якщо п=2k, тоді
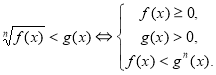
-
Якщо п=2k+1, тоді
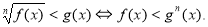
Розглянемо приклади:
1)![]() ; 2)
; 2)![]() ; 3)
; 3)![]() ; b>0
; b>0
![]()
![]()
![]()
![]() .
. ![]() .
. ![]() .
.
4) ![]() ; 5)
; 5) ![]() ;
;
![]()
![]()
![]() .
. ![]() .
.
![]() .
. ![]() .
.
6) ![]()
![]() .
.
7) ![]() ;
;
![]()
![]() Розв’яжемо другу нерівність методом інтервалів:
Розв’яжемо другу нерівність методом інтервалів:
. Виберемо інтервал: ![]() .
.
4 5
Тоді з об’єднання розв’язків системи нерівностей
одержимо: ![]()
![]()
8) ![]() ;
;
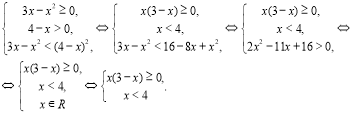
![]() Визначимо об’єднання розв’язків отриманої системи на числовій осі: .
Визначимо об’єднання розв’язків отриманої системи на числовій осі: .
0 3 4
Виберемо інтервал: ![]()
9) ![]()
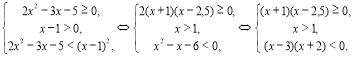
Скориставшись методом інтервалів встановимо об’єднання розв’язків системи:
![]()
![]()
![]() .
.
–1 2,5 1 –2 3
Виберемо інтервал: ![]()
Розв’яжіть самостійно:
1. ![]() ; 2.
; 2. ![]() ; 3.
; 3. ![]() ;
;
4. ![]() 5.
5. ![]() 6.
6. ![]() .
.
Нерівності, в яких невідоме входить до показника степеня, називаються показниковими.
Найпростіші показникові нерівності – це нерівності виду: ах>b або ах<b(ах≥b або ах≤b ); a>0; b>0; a≠1.
Розв’язування найпростіших показникових нерівностей.
1. 5х-1 > 25
5х-1 > 52
y=5t-зростаюча функція, тому: х-1>2, x>3.
2. (0.5)х-1 > 1
![]()
y=(0.5)х- спадна функція, тому: х-1<0 , x<1.
3. 5х-1>-5 функція ах>0, тому: ![]() .
.
4. (0.5)х-1>4
![]()
y=(0.5)х- спадна функція, тому: х-1<–2 , x<–1.
5. 5х-1<0
6. 5х-1<-2
Обидві нерівності не мають розв’язків, оскільки 5х>0: для всіх х![]() R.
R.
Зведення показникових нерівностей до найпростіших шляхом зведення до спільної основи.
7. 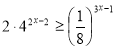
Зведемо обидві частини нерівності до основи 2:![]()
21(22)2х-2 (2-3)3х-1 ![]() 24х-3 2-9х+3
24х-3 2-9х+3
y=2х-зростаюча, тому: 4х-3 -9х+3![]() 4х+9х 3+3
4х+9х 3+3![]() 13х 6
13х 6
![]() х6/13.
х6/13.
Зведення показникових нерівностей до найпростіших шляхом винесення спільного множника за дужки.
8. 34х + 24х+1 + 34х+2 236
Винесемо за дужки спільний множник (множник з найменшим з наявних показників)
4х(3 + 24 + 342) 236
4х 59 236 зведемо до однієї основи:
4х 4; х 1.
Зведення показникових нерівностей до найпростіших шляхом ділення лівої і правої частин на один зі степенів.
9. 5x-2<72-x
Домножимо обидві частини нерівності на 7x-2>0:
(57)x-2 < 72-x 7x-2
зведемо обидві частини до однієї основи використовуючи
властивості ![]() ;
;
35x-3 < 70, 35x-3 < 1, 35x-3 <350 , х-3<0, х<3.
Зведення показникових нерівностей до квадратних шляхом введення нової змінної.
10. ![]()
введемо заміну змінних 2x= t, t>0
Розв’яжемо одержану нерівність відносно змінної t:
t2-3 t+2 0, t>0;
(t-1)(t-2) 0, t>0;
![]()
0 1 2 t 1≤t≤2
Повернемося до заміни і розв’яжемо показникову
нерівність: 1≤2x≤2;
0≤х≤1.
Зведення показникових нерівностей до квадратних шляхом почленного ділення на один зі степенів.
11. 222х6х+39х
Перепишемо цю нерівність в іншому вигляді:
222x 2х3х+332х.
Розділимо обидві частини нерівності на 32x>0.
Одержимо: ![]()
Зробимо заміну: ![]() х=t, t>0; 2t2-t-3 0, t>0
х=t, t>0; 2t2-t-3 0, t>0
Розв’яжемо одержану нерівність, враховуючи, що t>0:
![]() 2(t–1.5)(t+1) 0, t>0 –1 0 1.5 t
2(t–1.5)(t+1) 0, t>0 –1 0 1.5 t
Одержимо: t 1.5
Повернемося до заміни і розв’яжемо показникову нерівність:![]() ; х -1.
; х -1.
ауваження! При розв’язувані показникових нерівностей слід обов’язково враховувати монотонність показникових функцій. Якщо основа показникової функції менша від одиниці, тоді знак нерівності міняється на протилежний.
Розв’яжіть самостійно:
-
49х<
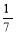 .
.
-
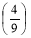 х>
х>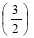 х+1.
х+1.
- 2х-11.
-
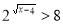 .
.
- 2х+2-2х>96.
- 9x+23x-15>0.
- 3x+3x+2<30.
- 11х-7<177-х.
- 2x-2>5.
Нерівності, які містять невідоме під знаком логарифма називаються логарифмічними.
При розв’язуванні логарифмічних нерівностей слід пам’ятати:
- загальні властивості нерівностей;
- властивість монотонності логарифмічної функції;
- область визначення логарифмічної функції.
Основні методи розв’язування логарифмічних нерівностей:
|
a>1 |
0<a<1 |
|
log a f(x) > b 0< f(x)<ab |
|
log a f(x) < b f(x)> ab |
|
logg(x) f(x)<b |
|
4) loga f(x)>loga h(x) |
loga f(x)>loga h(x) |
|
5) loga f(x)<loga h(x) |
loga f(x)<loga h(x) |
|
6) logg(x) f(x)<logg(x) h(x) |
|
|
7) logg(x) f(x)>logg(x)h(x) |
|
Розглянемо приклади:
1. log2 (x2 +3x) 2.
Запишемо число 2 у вигляді логарифма за основою 2:
log 2 (x2 +3x) log 2 4.
Встановимо монотонність функції: 2>1; y = log2x – зростає.
Замінимо нашу нерівність рівносильною системою нерівностей:
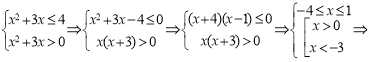
![]() .
.
2. log (х-3) (x–1) <2.
log (х-3) (x–1) < log (х-3) (x–3)2.
Розв’яжемо сукупність двох систем нерівностей:
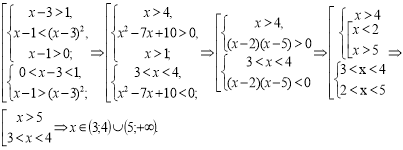
3. ![]() ОДЗ: х>0.
ОДЗ: х>0.
![]() Введемо заміну змінних log0,5x = t, методом інтервалів розв’яжемо нерівність:
Введемо заміну змінних log0,5x = t, методом інтервалів розв’яжемо нерівність:
t2+ t –2 0
(t + 2)(t - 1) 0 –2 1 t
–2 t 1
Повернемося до заміни і розв’яжемо систему логарифмічних нерівностей з урахуванням ОДЗ:
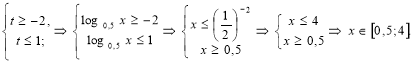
4. log 0,4 x+ log 0,4 (x-1) log 0,4 (x+3).
Суму логарифмів замінимо логарифмом добутку з урахуванням ОДЗ і складемо систему нерівностей:
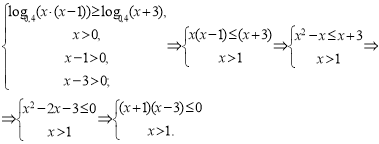
Відповідь: 1<x3.
5. (3-2x) log0,1 x < 0
Дану нерівність розв’яжемо методом інтервалів. Знайдемо ОДЗ: х >0.
Знайдемо нулі функції: (3-2х) log0,1 x = 0; 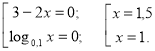
На числову вісь нанесемо ОДЗ і нулі функції.
![]()
0 1 1.5 х
Встановимо знак функції на кожному проміжку ОДЗ і запишемо відповідь: х (1;1,5).
Розв’яжіть самостійно:
-
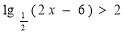 .
.
- log 3 (x - 2) > 1.
- log 8 (x2 - 4x+3) < 1.
- log x+1 (x - 2) < 0.
- log 0.5(2x +3) < log 0.5(4x – 1).
-
log3log0,2log32
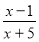 ≤ 0.
≤ 0.
-
5 log0,5х≤6+
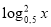 .
.
- log 3 x + log x 9 > 2.
2.7. Тригонометричні нерівності
Тригонометричними називають нерівності, які містять невідому під знаком тригонометричної функції (sin, cos, tg,ctg).
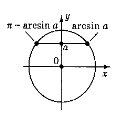
Для розв’язування найпростіших тригонометричних нерівностей використовується одиничне коло і властивості тригонометричних функцій.
|
|
|
a < -1 |
- 1<а<1 |
a > 1 |
|
sin t > a |
|
|
розв'язків не має |
|
|
sin t < a |
не має розв'язків |
|
|
|
|
|
|
b < -1 |
|
b > 1 |
|
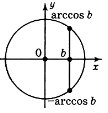
cos t > b |
|
|
не має розв'язків |
|
|
cos t < b |
не має розв'язків |
|
|
|
|
|
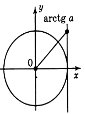
tg t >a |
|
||
|
tg t <a |
|
|||
|
|
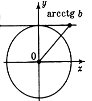
ctg t>b |
|
||
|
ctg t<b |
|
|||
Розглянемо приклади.
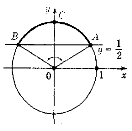 1. Розв'яжіть нерівність
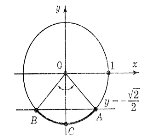
1. Розв'яжіть нерівність ![]()
Будуємо одиничне коло та пряму ![]() , яка перетинає одиничне коло в точках А і В. Знаходимо на одиничному колі точки, значення координат які не менші
, яка перетинає одиничне коло в точках А і В. Знаходимо на одиничному колі точки, значення координат які не менші ![]() .
.
Цими точками є точки дуги АСВ, де ![]()
Отже, розв'язком нерівності будуть усі значення t із проміжку ![]() .
.
Враховуючи, що період функції sin t дорівнює 2π, маємо розв'язок даної нерівності ![]()
Відповідь: ![]()
 2. Poзв’язати нерівність
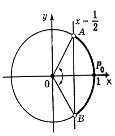
2. Poзв’язати нерівність ![]()
Будуємо одиничне коло та пряму ![]() , яка перетинає одиничне коло в точках А і В.
, яка перетинає одиничне коло в точках А і В.
Точки дуги А і В мають значення у, не більші за ![]() , де
, де ![]()
Отже, розв'язком нерівності будуть усі значення t![]()
![]() .
.
Враховуючи періодичність маємо: ![]() .
.
Відповідь:![]()
 3. Розв'язати нерівність
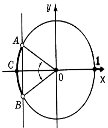
3. Розв'язати нерівність ![]() .
.
Побудуємо одиничне коло та пряму ![]() , яка перетинає одиничне коло в точках А і В. Точки одиничного кола, абсциси яких більші за
, яка перетинає одиничне коло в точках А і В. Точки одиничного кола, абсциси яких більші за ![]() , лежать на дузі АР0В, де
, лежать на дузі АР0В, де ![]()
Отже, розв'язком нерівності будуть усі значення t із проміжку ![]() .
.
Враховуючи періодичність, маємо:![]()
Відповідь: ![]()
 4. Розв'язати нерівність
4. Розв'язати нерівність ![]()
Побудуємо одиничне коло та пряму ![]() , яка перетинає одиничне коло в точках А і В.
, яка перетинає одиничне коло в точках А і В.
Точки одиничного кола, абсциси яких менші за ![]() , лежать на дузі АСВ де
, лежать на дузі АСВ де ![]()
Отже, розв'язком нерівності будуть усі значення t![]()
![]() .
.
Враховуючи періодичність, маємо: ![]()
Відповідь: ![]()
5. Розв'яжіть нерівність ![]()
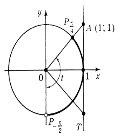 Побудуємо одиничне коло та лінію тангенсів. На осі тангенсів позначимо число 1. Якщо t є розв'язком нерівності, то ордината точки Т, рівна tg t, повинна бути не більша 1. Множина таких точок T — промінь AT. Множина точок Pt, що відповідають точкам променя AT, — дуга
Побудуємо одиничне коло та лінію тангенсів. На осі тангенсів позначимо число 1. Якщо t є розв'язком нерівності, то ордината точки Т, рівна tg t, повинна бути не більша 1. Множина таких точок T — промінь AT. Множина точок Pt, що відповідають точкам променя AT, — дуга ![]() яка на рисунку виділена. (Зверніть увагу: точка
яка на рисунку виділена. (Зверніть увагу: точка ![]() належить, а точка
належить, а точка ![]() не належить множині розв'язків).
не належить множині розв'язків).
Отже, розв'язком нерівності будуть усі значення t![]()
![]() Враховуючи, що період функції tg t дорівнює π, маємо розв'язок даної нерівності
Враховуючи, що період функції tg t дорівнює π, маємо розв'язок даної нерівності ![]()
Відповідь: ![]() , де
, де ![]()
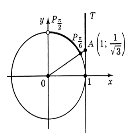 6. Розв'яжіть нерівність
6. Розв'яжіть нерівність ![]()
На осі тангенсів позначимо число ![]() і множину значень тангенсів, не менших за
і множину значень тангенсів, не менших за ![]() (промінь AT). На одиничному колі множина точок, що відповідають кутам, тангенс яких не менший від
(промінь AT). На одиничному колі множина точок, що відповідають кутам, тангенс яких не менший від ![]() , є дуга
, є дуга ![]()
Отже, розв'язком нерівності будуть усі значення t ![]()
![]()
Враховуючи періодичність, маємо: ![]() де
де ![]() .
.
Відповідь: ![]() , де n є Z.
, де n є Z.
7. Розв'яжіть нерівність ![]()
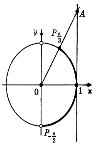 Розглянемо два способи розв’язування даної нерівності.
Розглянемо два способи розв’язування даної нерівності.
1 спосіб. Враховуючи, що ![]() маємо
маємо ![]() тоді маємо нерівність
тоді маємо нерівність ![]() , або
, або ![]()
Розв'яжемо останню нерівність на колі, маємо:
![]()
![]()
Відповідь: ![]() де
де ![]()
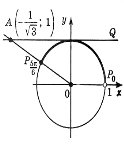 2 спосіб. На осі котангенсів позначимо число
2 спосіб. На осі котангенсів позначимо число ![]() і множину значень котангенсів, не менших за
і множину значень котангенсів, не менших за ![]() (промінь AQ). На одиничному колі множина точок, що відповідають кутам, котангенс яких не менший від
(промінь AQ). На одиничному колі множина точок, що відповідають кутам, котангенс яких не менший від ![]() , є дуга
, є дуга ![]() . Отже, розв'язки нерівності будуть усі значення t
. Отже, розв'язки нерівності будуть усі значення t![]()
![]()
Враховуючу періодичність, маємо: ![]() , де
, де ![]() .
.
Відповідь: ![]() , де
, де ![]() .
.
Розв’яжіть самостійно:
- sin x > 0,5.
-
cos x <
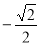 .
.
-
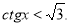
-
tg
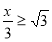 .
.
-
sin (
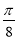 +
+ 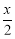 ) < 0.
) < 0.
-
tg (3x–
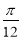 ) >
) >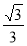 .
.
-
cos (2x – 1) ≤
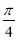 .
.
-
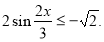
-
2 соs
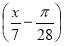 – 2 > 0.
– 2 > 0.
-
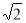 sin
sin 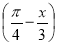 + 1 < 0.
+ 1 < 0.
-
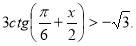
-
3 –
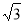 tg
tg 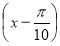 < 0.
< 0.
- 3 ctg (2x + 6) – 9 > 0.
Тригонометричні нерівності, що зводяться до квадратичних:
Якщо тригонометрична нерівність в результаті тотожних перетворень зводиться до виду:
asin2x+bsinx+c>0 або acos2x+bcosx+c>0
asin2x+bsinx+c<0 acos2x+bcosx+c<0,
тоді вводять підстановку: y=sinx (y=cosx), причому |у|≤1.
Отримують нерівність виду: aу2+bу+c>0 або aу2+bу+c<0.
Розв’язавши алгебраїчну нерівність, повертаються до заміни змінних. Розв’язують найпростішу тригонометричну нерівність, яка одержана в результаті підстановки.
Наприклад,
Розв’язати нерівність: 2sin2x+sinx–1<0.
![]() Нехай sinx=у, тоді 2у2+у–1<0, розв’язуємо цю нерівність:
Нехай sinx=у, тоді 2у2+у–1<0, розв’язуємо цю нерівність:
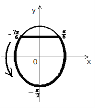 2у2+у–1=0, у1=–1, у2=0.5;
2у2+у–1=0, у1=–1, у2=0.5;
–1<y<0,5. –1 0,5 y
Нерівність зводиться до розв’язування системи: ![]()
Відповідь: ![]()
Розв’яжіть нерівності, що зводяться до квадратичних:
-
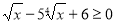 .
.
-
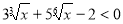 .
.
-
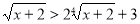 .
.
-
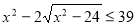 .
.
- 52х – 30 · 5х + 125 > 0.
- 4х – 10 · 2х-1 – 24 < 0.
- 3 lg2(x – 1) – 10 lg(x – 1) + 3 ≥ 0.
-
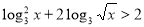 .
.
-
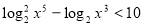 .
.
-
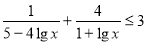 .
.
-
2соs2
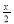 – cos
– cos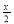 – 1 > 0;
– 1 > 0;
- 2соs2 x – 7sin x – 5 < 0;
- tg 5x + 3ctg 5x + 4 < 0;
- 2sin x – 3 cos x >0.
- 3sin2x–7sinxcosх+4cos2x<0.
- 22cos2 x + 4sin 2x>7.
Список використаної літератури
- О.М. Афанасьєва, Я.С.Бродський та інші “Математика”, - Київ, “Вища школа”, 2001 р.
- О.М. Афанасьєва, Я.С.Бродський та інші “Дидактичні матеріали з математики”, - Київ, “Вища школа”, 2001 р.
- М.І.Шкіль, З.І.Слєпкань, О.С.Дубинчук “Алгебра і початки аналізу”, - Київ, “Зодіак-Еко”, 2000 р.
- М.В.Богомолов “Практичні заняття з математики”, - Київ, “Вища школа”, 1979 р.
- М.І.Сканаві “Збірник задач з математики для вступників до втузів”, - Київ, “Вища школа”, 1996 р.
- Г.М.Яковлєв “Алгебра і початки аналізу”, - Київ, “Вища школа”, 1984 р.
- Л.О.Сморжевський, П.С.Атаманчук, А.М.Кух “Задачі з алгебри і початків аналізу 10-11”,- Київ, “А.С.К.”, 1999 р.
- Збірник завдань для державної підсумкової атестації з математики. 11 клас.
- Роєва Т.Г., Хроленко Н.Ф. “Алгебра у таблицях 10 клас”,-Харків, видавнича група “Академія”, 2001 р.
- Фридман Л.М., Турецький Е.Н. “Как научиться решать задачи”, - Москва, «Просвещение», 1984 г.
- Бондаренко М.Ф. та інші “Математика для вступників до вузів” за редакцією проф. Семенця В.В., Харків, «Компанія СМІТ», 2002 р.
- Олійник Лариса “Алгебраїчний тренажер”, Тернопіль, «Підручники і посібники», 2008 р.
Зміст
1. Нерівності. Основні поняття.
2. Вчимося розв’язувати нерівності.
Умовні позначення числових проміжків
2.7. Тригонометричні нерівності
Тригонометричні нерівності, що зводяться до квадратичних:
Список використаної літератури
1


про публікацію авторської розробки
Додати розробку