Практикум "Підготовка до ЗНО" (№1). Розв'язування нерівності з параметром.
Про матеріал
Практикум по підготовці до ЗНО з математики №1. Презентація з розв'язуванням задачі №33 основної сесії ЗНО 2018 року. Матеріал можна використовувати на уроках алгебри і початків аналізу у кінці навчального року при повторенні або на додаткових заняттях. Перегляд файлу


залежно від значень параметра a.
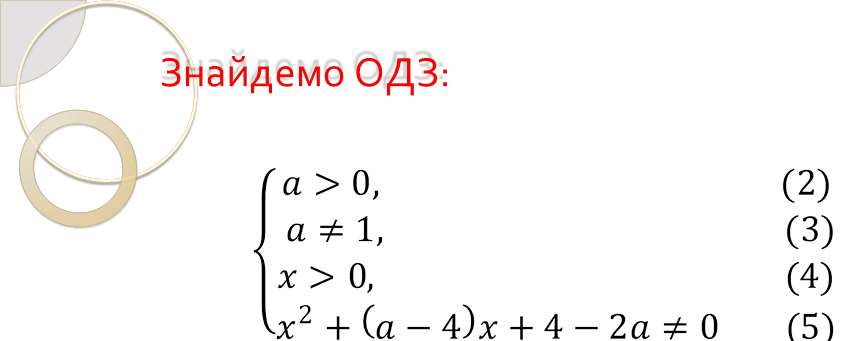
Із рівняння (5) ![]() −
−![]() −
−![]()
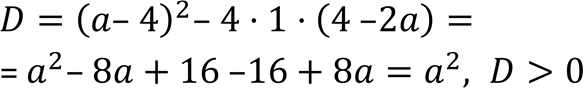
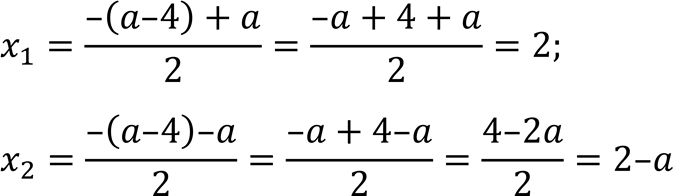 .
.
Нерівність можна записати: 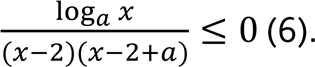
ОДЗ набуває вигляду:
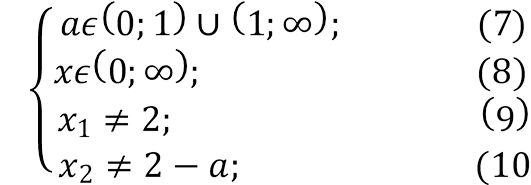
Нуль функції: log𝑎 𝑥 = 0; 𝑥 = 𝑎0 = 1.
Нанесемо нулі функції та ОДЗ на координатну вісь:
Розглянемо 7 випадків розташування кореня 𝑥2.
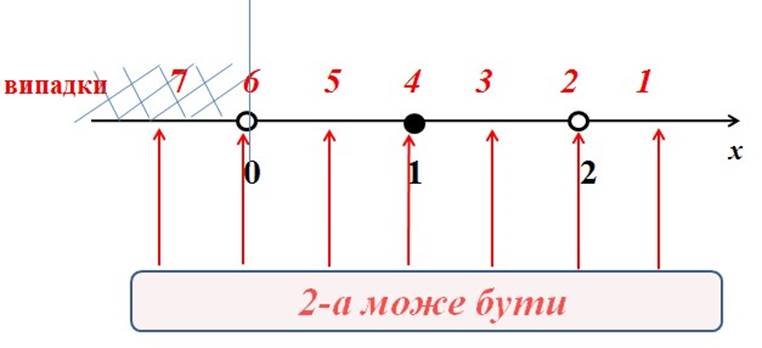
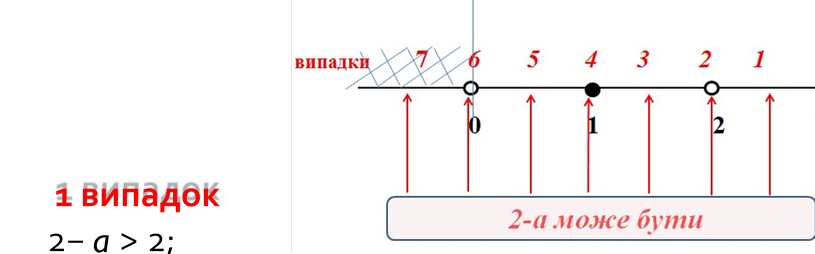
−a > 2 − 2 | · (− 1);
a ˂ 0 – суперечить умові (7), не входить в ОДЗ;
 2 випадок
2 випадок
2 − a = 2;
−a = 2 − 2;
a = 0 – суперечить умові (7), не входить в ОДЗ;
3 випадок
1 ˂ 2−a ˂ 2 | − 2;
 −1
˂ − a ˂ 0 | ·(− 1 );
−1
˂ − a ˂ 0 | ·(− 1 );
0 ˂ a ˂ 1 , тоді визначимо знаки на проміжках за нерівністю (6):
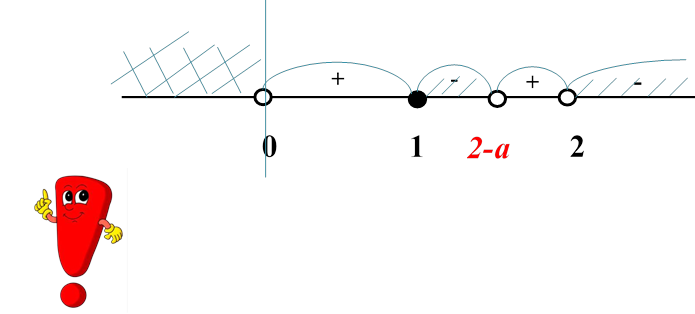 𝑥𝜖[1; 2 − 𝑎) ∪
(2; ∞)
𝑥𝜖[1; 2 − 𝑎) ∪
(2; ∞)
![]()
− ![]() ˂ − a
˂ −
˂ − a
˂ − ![]() | · (−
| · (−
![]() );
);
 |
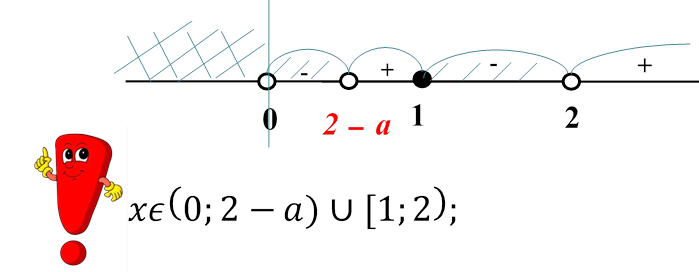
 |
визначимо знаки на проміжках за нерівністю (6):
![]()

![]() якщо a
𝜖
0; 1
якщо a
𝜖
0; 1![]() , то 𝑥𝜖 1; 2 − 𝑎
, то 𝑥𝜖 1; 2 − 𝑎![]() ∪
∪ ![]() 2; ∞
; якщо a 𝜖(1;
2), то 𝑥𝜖0;
2 − 𝑎) ∪ [1; 2;
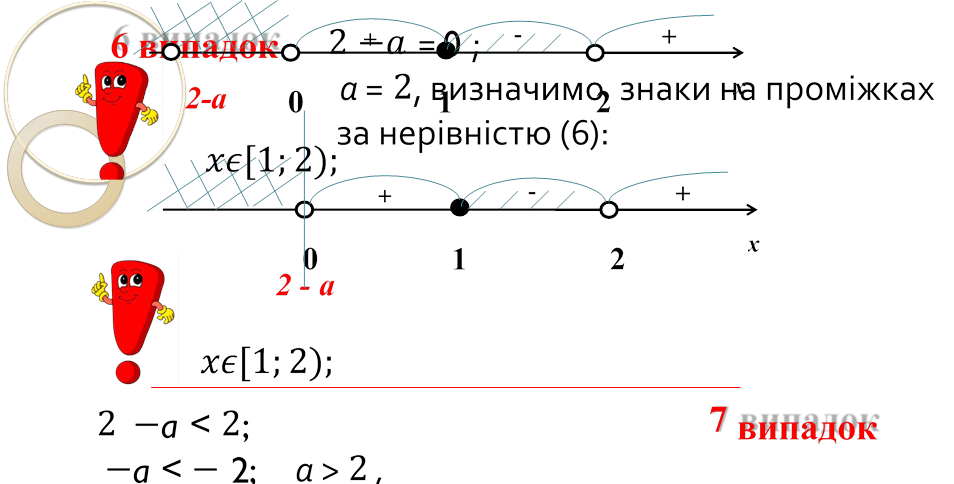
якщо a 𝜖[2;
∞], то 𝑥𝜖[1;
2).
2; ∞
; якщо a 𝜖(1;
2), то 𝑥𝜖0;
2 − 𝑎) ∪ [1; 2;
якщо a 𝜖[2;
∞], то 𝑥𝜖[1;
2).
Середня оцінка розробки
Оцінки та відгуки
pdf
Оцінка розробки


Безкоштовний сертифікат
про публікацію авторської розробки
про публікацію авторської розробки
Щоб отримати, додайте розробку
Додати розробку
