Урок з теми "Властивості та графіки тригонометричних функцій. Гармонічні коливання."

Тема 3. Тригонометричні функції                      

 Тема уроку : Властивості та графіки тригонометричних функцій. Гармонічні коливання.

 Мета уроку: Навчити учнів будувати графіки тригонометричних функцій,використовуючи геометричні перетворення графіків функцій. Розвивати графічні навички учнів, логічне та аналітичне мислення, математичну мову учнів, вміння обґрунтовувати відповідну дію. Формувати інтерес до знань, навички самостійної праці, навички роботи в групі.

Обладнання: мультимедійний проектор, лінійка, кольорова крейда, картки.

                                  Хід уроку

І. Організаційний етап.

Налаштування учнів на роботу. Перевірка готовності учнів до уроку.

ІІ. Актуалізація опорних знань учнів та повторення матеріалу.

1. Перевірка виконання домашнього завдання (фронтально).

2. Повторення.

Завдання «Збери формулу»

Встановити відповідність між лівою ( на дошці) та правою частинами ( на картках в учнів) формул:

sin² α + cos² α = l

соs (α – β) = соs α · соs β + sіn α · sіn β.            

соs (α + β) = соs α · соs β – sіn α · sіn β;               

sіn (α + β) = sіn α · соs β + соs α · sіn β;                

sіn (α – β) = sіn α · соs β – соs α · sіn β;                

ІІІ. Мотивація навчальної діяльності.

Гармонічні коливання.

Сьогодні на уроці ми продовжимо вивчення тригонометричних функцій. Мета нашого уроку – розглянути приклади коливальних рухів, описати їх за допомогою математичних законів; навчитися будувати графіки тригонометричних функцій.

Коливальний рух. Це рух, який повторюється через певний інтервал часу.

Приклади коливальних рухів: рух тіла по колу, голки  швейної машинки, коливання гілки дерева на вітрі і т. п.

Людина  зустрічається   з коливаннями і використовує їх у різних сферах своєї діяльності, наприклад: звуки та слух, фізичні основи будови голосового апарата людини та тварин, звукові методи дослідження в клініці. Графіки тригонометричних функцій описують гармонічні коливання.

IV. Вивчення нового матеріалу.

1. Робота з картками,  на яких зображені графіки тригонометричних функцій.

Усно:  пояснити, за допомогою яких геометричних перетворень графіків функцій  y = sin x та  y = cos x побудовані графіки даних функцій. Учні мали дома повторити геометричні перетворення графіків функцій.

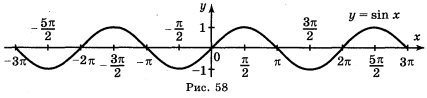
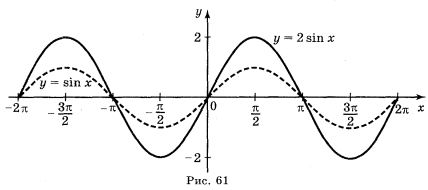
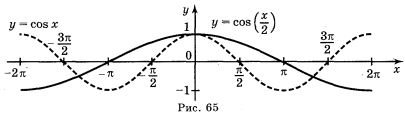
2. Використовується мультимедійний проектор. Презентація «Побудова графіків тригонометричних функцій»

3. Робота учнів біля дошки.

1) На дошці зображено системи координат. Учні мають завдання побудувати  графіки функцій:  y = cos x;  y = sin x. ( біля дошки працює два учні ).

2) Використовуючи геометричні перетворення графіків функцій, побудувати графіки таких функцій: y = cos x – 3;  y = 2cos x-1;  y = sin (x - π/3);  y = |sinx |

( за виконану роботу учні отримують оцінки ).

Учні класу в зошитах будують також графіки заданих функцій самостійно. Роботи перевіряються фронтально і обговорюються допущені помилки.

V. Застосування вмінь.

Самостійна робота.

Учні отримують картки, на яких зображені системи координат. Завдання: побудувати графіки функцій.

І варіант.

y = 2cos x + 1

y = cos (x-)

y = sin( x + )

y = |sin x|

ІІ варіант.

y = cos x +3

y = |cos x|

y = 2sin x-1

y = sin( x-)

VI. Підсумок уроку. 

До учнів  ставиться запитання: 1) чи досягнуто мети уроку?  2) які знання учні отримали на уроці? ( відповіді окремих учнів ).

V. Домашнє завдання.

1. Побудувати графіки функцій:

y = 2sin (x+π/3);     y = 0.5cos x – 1

2. Повторити значення синусів, косинусів, тангенсів від 0 до 180⁰