Урок "Застосування похідної. Загальне дослідження функції за допомогою похідної та побудова графіка"
Тема: Застосування похідної. Загальне дослідження функції за допомогою похідної та побудова графіка
Мета: - перевірити рівень засвоєння учнями вмінь і навичок проводити загальне дослідження функцій, будувати їх графіки на основі цього дослідження; розв’язувати задачі на застосування правила визначення найбільшого та найменшого значень функції на відрізку;
- розвивати логічне мислення учнів,пам'ять, розумову активність,уміння порівнювати, аналізувати, узагальнювати та робити висновки;
- виховувати самостійність, організованість, дисципліну, культуру письма та уміння працювати в парах, групах та індивідуально.
Тип уроку: удосконалення знань та вмінь.
«Теорія без практики мертва
або безплідна і практика без
теорії неможлива. Для теорії
потрібні знання, для практики,
крім того, - і уміння.»
А.М.Крилов
Хід уроку
І. Оргмомент.
ІІ. Перевірка домашнього завдання.
Обговорення запитань, які виникли під час виконання домашнього завдання.
ІІІ. Актуалізація опорних знань.
Математичний диктант. «Закінчити речення»
- Критичними точками функції називаються …(внутрішня точка області визначення функції, у якій похідна дорівнює нулю або не існує).
-
Критичні точки функції
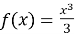 -
- - 6x – це точки…(-2 і 3).
- 6x – це точки…(-2 і 3).
-
Критичними точками функції
 є точки…(х=
є точки…(х=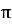 п, пєZ).
п, пєZ).
- Критичні точки функції …(обов’язково чи не обов’язково) є точками екстремуму цієї функції.(не кожна точка є екстремумом даної функції).
- Якщо x0 є точкою екстремуму функції f(x)і в цій точці існує похідна, то…(х0 –є точкою тіп або тах).
- Якщо функціяf(x)неперервна в точці x0і похідна f’’(x) при переході через точкуx0змінює знак з плюса на мінус, то x0 є точкою…(х0-точка тах).
- Якщо функціяf(x)неперервна в точці x0і похідна f’’(x) при переході через точкуx0змінює знак з мінуса на плюс, то x0 є точкою…(х0-точка тіп).
- Точка x0=0 є точкою… (максимуму чи мінімуму) функції f(x)=x3-3x2+5(х0-точка максимуму).
- Точка x0=1 є точкою…(максимуму чи мінімуму) функції f(x)=-x3 -6x2+15x-3(х0-точкамінімуму).
- Екстремумом функції називається…(точка максимуму та мінімуму).
- Максимум функції f(x)= x3-6x2+5дорівнює…(х=0).
- Мінімум функції f(x)=-x3 -4,5x2-11 дорівнює…(х=-9).
ІV. Мотивація навчальної діяльності, оголошення теми та мети уроку.
Ще в XІX ст.. російський математик Панфуцій Львович Чебишев підкреслював, що «особую важность имеют те методы науки, которые позволяют решать задачу, общую для всей практической деятельности человека: как поступить со своими средствами (деньгами) для достижения наибольшей выгоды».
В наш час з такими проблемами зустрічаються представники різних спеціальностей: інженери-технологи проектують виробництво так, щоб товарів випускалося більше; конструктори літальних апаратів розробляють прилади з найменшою допустимою масою; економісти намагаються організувати зв'язок виробника з постачальником так, щоб затрати при транспортуванні виявилися мінімальними, і т.д.
V. Удосконалення знань і вмінь.
- Фронтальне опитування.
Повторення алгоритму дослідження функції.(Учні по черзі називають етапи дослідження функції, потім алгоритм вивішується на дошці.)
1) Знайти область визначення функції.
2) З’ясувати парність (непарність) функції.
3) З’ясувати періодичність функції.
4) Знайти точки перетину графіка функції з осями координат.
5) Знайти асимптоти графіка функції.
6) Знайти проміжки монотонності.
7) Визначити екстремуми функції.
8) Визначити проміжки опуклості графіка функції.
9) Побудувати графік функції, використавши результати дослідження.
- Робота в групах.
Організується диференційована робота в групах з урахуванням рівня навченості учнів.
Учитель пропонує учням об’єднатися в групи, до кожної з яких включаються учні з однаковим рівнем підготовки. Кожна група отримує картку із завданнями. Учитель працює з учнями, які виконують завдання середнього рівня. Інші учні працюють самостійно, консультуючи один одного.
|
|
Картка № 1 |
Картка № 2 |
|
|
1.Обчислити похідну та знайти її значення при вказаному аргументі: |
|
|
Рівень А |
у=4х3+6х+3, х0=-2 (В: у /(-2)=54) |
у=7х3-8х+3, х0=-2(у /(-2)=76) |
|
Рівень В |
у= |
у= |
|
Рівень С |
у= (х-3) |
у= (х2-1) |
|
|
2. Дослідити функцію та побудувати її графік |
|
|
Рівень А |
у=х3-3х2+2(В: утах(0)=2; утіп(2)=-2) |
у=х3-2х2+х(В: утах( |
|
Рівень В |
у= |
у= |
|
Рівень С |
у= х |
у= х |
3. Колективне виконання вправ.
1) Число 64 подати у вигляді суми двох додатних доданків так, щоб сума їх квадратів була найменшою. (Розглядаємо функцію S(x)=x2+(64-x)2 на проміжку (0;64))
2) Парканом довжиною 80 м потрібно огородити прямокутну ділянку найбільшої площі. Знайти розміри ділянки. (Розглядаємо функцію S(x)=x(40-x) проміжку (0;40))
4. Робота в парах.
За результатами попередньої роботи створюються гетерогенні пари типу «вчитель-учень» з метою допомогти більш слабкому учню оволодіти базовим рівнем знань.
- Визначити проміжки зростання і спадання функції:
а) f(x)=3x4(В:f/(x)![]() ; f/(x)
; f/(x)![]() ; б)f(x)=x2-6x+10(В:f/(x)
; б)f(x)=x2-6x+10(В:f/(x)![]() ; f/(x)
; f/(x)![]()
2) Визначити проміжки зростання і спадання функції та точки екстремуму функції:
f(x)=2x3-3x2-12x+36(В:f/(x)![]() ;f/(x)
;f/(x)![]() ; fтах(-1)=43; fтіп(2)=16).
; fтах(-1)=43; fтіп(2)=16).
3)Знайти найбільше і найменше значення функції на заданому проміжку:
f(x)=![]() ; [-4;1](В:fтах(-3)=1;fтіп(1)=-1).
; [-4;1](В:fтах(-3)=1;fтіп(1)=-1).
4) Дослідити функцію і побудувати її графік:f(x)=3x2-x3.
5) Число 24 подати у вигляді суми двох додатних доданків так, щоб сума їх квадратів була найменшою.
Учитель спостерігає за роботою пар, але втручається в роботу пар тільки тоді, коли в учнів виникають запитання і вони самі звертаються по допомогу до вчителя.
5. Самостійна робота.
Кожен учень отримує різнорівневі завдання.
- (1б). Чому дорівнює похідна функції f(x)=(3x-1)5?
- 15(3x-1)4; Б) 5(3x-1)4; В) 3(3x-1)4; Г) 15(3x-1)6.
-
(1б). Знайти похідну функції f(x)=
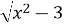
-
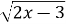 ;Б)
;Б) 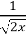 ;В)
;В)  ; Г)
; Г)  .
.
-
(1б). Обчисліть f/(
 ), якщо f(x)=
), якщо f(x)=
А) 1; Б) ![]() ; В) -
; В) -![]() ; Г)
; Г) ![]() .
.
4. (1б). Відомо,що f(x)=(x2-1)3; g(x)=(x3-1)2. Порівняйте f '(2) іg'(2).
А) f '(2) >g'(2);Б) f '(2) <g'(2); В)f '(2) =g'(2);
Г) порівняти неможливо.
5. (2б). Установіть відповідність між заданими функціями та їхніми похідними.
|
1 |
f(x)=cos2x+3 (Б) |
А |
f '(x)= |
|
2 |
f(x)=sin2x-3 (А) |
Б |
f '(x)= |
|
3 |
f(x)= |
В |
f '(x)= |
|
4 |
f(x)= |
Г |
f '(x)= |
|
|
|
Д |
f '(x)= |
6. (2б). Знайдіть f '(-1), якщо f (x)=(x2-2x+6)2-(x2+2x-6)2 (В:-72)
7. (2б). Знайдіть точки екстремуму функції f (x)=3![]() -0,5x (В:
-0,5x (В:![]()
8. (2б). Дослідіть функціюf '(x)=x4-5x2+4 і побудуйте її графік.
Під час виконання самостійної роботи учитель уважно стежить за роботою учнів і за потреби допомагає їм.
VІ.Рефлексія набутих знань. Підсумок уроку.
Ми узагальнили та повторили алгоритм дослідження функції за допомогою похідної. Ще раз пригадуємо етапи дослідження та звертаємо увагу на завдання, які зустрічаються на ЗНО.
Оцінювання учнів.
VІІ. Домашнє завдання (різнорівневе).
- Підготуватися до контрольної роботи.
- Завдання за підручником: повторити вивчений матеріал.
- Додаткове завдання:
а) Щоб загородити клумбу, що має форму кругового сектора, потрібно взяти дріт довжиною 2м. Яким має бути радіус круга, щоб площа сектора була найбільшою?
б) Тіло рухається за законом s(t)=9t2-2t3. Яка найбільша швидкість тіла?


про публікацію авторської розробки
Додати розробку
