Урок «Застосування показникової функції до розв`язування прикладних задач»

11 клас. Алгебра і початки аналізу

Урок «Застосування показникової функції до розв`язування прикладних задач»

Епіграф уроку: природа формулює свої закони мовою математики.

Галілео Галілей

Міжпредметні зв`язки: математика, фізика, біологія, географія, екологія.

Мета: формування в учнів умінь:

 застосовувати набуті знання у реальних життєвих ситуаціях, під час розв'язання практичних завдань та здатності визначати і обґрунтовувати власну життєву позицію;

читати і будувати графіки функціональних залежностей, досліджувати їх властивості;

розвивати спостережливість, увагу, пам’ять, уяву, мислення; вироблення звички до планування своїх дій;

самостійно контролювати проміжні і кінцеві результати роботи.

                                             Хід уроку

Завдання №1. Моделювання радіоактивного розпаду.

                                      (практична робота)

      Із курсу фізики відомо, що під час радіоактивного розпаду маса радіоактивної речовини за рівні проміжки часу зменшується в одну і ту ж саму кількість разів. Показникова функція описує цей процес. Ваша задача: змоделювати радіоактивний розпад, перевірити на моделі закон радіоактивного розпаду.

Обладнання: 128 однакових монет, два паперові (пластикові) стакани, таця, кольорові олівці (ручки), міліметровий папір. 

ОПИС МОДЕЛІ

Розпад того чи іншого ядра — подія випадкова. Такою самою випадковою подією є випадання «герба» або «цифри» після кидка монети. Тому для моделювання радіоактивного розпаду використаємо таку модель.

Ядра в радіонуклідному зразку змоделюємо монетами в паперовому стакані: нехай ядру, що не розпалося, відповідає монета, на якій випаде «герб»; ядру, що розпалося, — монета, на якій випаде «цифра». Тоді кожен кидок купи монет відповідатиме періоду піврозпаду Т_1/2 (часу, за який розпадається половина ядер радіонукліда в зразку), а кількість n кидків — кількості періодів піврозпаду, тобто часу t спостереження: t = nΤ_1/2.

ВКАЗІВКИ ДО РОБОТИ

Суворо дотримуйтесь інструкції з безпеки .

Результати вимірювань відразу заносьте до таблиці.

Підготовка до експерименту

1. Підготуйте три таблиці — одну для кожної серії кидків (див. зразок).

2. Покладіть 128 монет у паперовий стакан.

Експеримент

1. Перемішайте монети в паперовому стакані й висипте їх на тацю (рис. 1). Полічіть число монет, на яких випав «герб» (тобто число ядер, що не розпалися), і покладіть їх у стакан. Монети, на яких випала «цифра» (тобто ядра, що розпалися), покладіть в інший стакан та відставте його.

Рис. 1

2. Перемішайте монети, на яких випав «герб», висипте їх на тацю і знову полічіть число монет, на яких випав «герб». Повторюйте цей дослід, доки не залишиться одна монета з «гербом», але не більше ніж ще 6 разів. (Таким чином, усього ви повинні зробити максимум 8 кидків.)

3. Повторіть серію кидків (дії, описані в пунктах 1-2) ще 2 рази.

Серія кидків ____ (колір графіка) ____)

Опрацювання результатів експерименту

1. На міліметровому папері для кожної серії кидків побудуйте відповідним кольором графік залежності Ν(n) — залежності числа N ядер, які не розпалися, від кількості кидків (приклад такого графіка див. на рис 2).

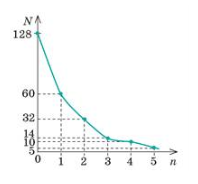
Рис. 2

2. У тих самих осях для кожної серії кидків побудуйте графік функції

 N = Ν₀ • 2^-n, яка виражає закон радіоактивного розпаду (вважайте, що початкова кількість ядер радіонукліда Ν₀ = 128).

3. Запишіть властивості графіка

Аналіз експерименту та його результатів

4. За результатами експерименту сформулюйте висновок, у якому поясніть, чому побудовані графіки не збігаються. Це є закономірністю чи використано недосконалу модель? Чи мають місце обидві причини?

Творче завдання

5. З’ясуйте, як вплине на якість моделі процесу радіоактивного розпаду, використаної в роботі:

а) збільшення кількості монет у 3 рази;

б) зменшення кількості монет у 3 рази.

Завдання №2 . Колективне розв`язування задач.

Показникова функція є математичною моделлю багатьох процесів, які відбуваються в природі або пов`язані з діяльністю людинию. Наприклад,  географам відомо що тиск повітря зменшується з висотою згідно формули

Р=Р₀ а ^h

№1

Обчислити яким буде атмосферний тиск на вершині Ельбрусу, висота якого 5,6 км, якщо залежність атмосферного тиску p від висоти (вираженої у кілометрах) h над рівнем моря виражається формулою:

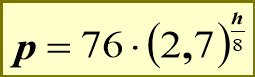
Розв`язування

№2.

    Чому дорівнює маса радіоактивного йоду, в кінці 4 діб з початку спостереження, якщо в початковий момент його маса складала 1 г, якщо період піврозпаду йоду дорівнює 8 діб.             

m₀ =1 г маса в початковий момент

 t = 4 доби

T = 8 діб

m – ?

Розв`язування:

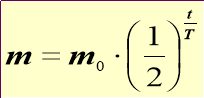
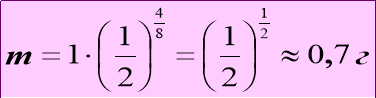
Відповідь: маса йоду 0,7 грама

Задача №3.

Прикладом швидкого розмножування бактерій є виготовлення дріжджів, під час якого по мірі росту бактерій проводиться відповідне додавання цукрової маси. Знайти масу дріжджів, якщо початкова маса складає 10 кг, а тривалість процесу 9 год.

m 0 – початкова маса дріжджів

t – час бродіння в годинах

m – маса дріжджів в процесі бродіння

Збільшення маси дріжджів виражається формулою показникової функції:

Розв`язування:

Відповідь: маса отриманих дріжджів 51,6 кг

Підсумок уроку. Ми  ще раз пере­коналися, що математика — це всеосяжна наука, без знання якої неможливо ні пізнати оточуючий нас світ, ні забезпечити науково-технічний прогрес. Як казав великий Ейнштейн : „Природа – це реалізація найпростіших математичних ідей”.

Домашнє завдання:1. Розв`язати задачу:

Визначити кількість населення світу у 2021 році, якщо у 2010 році на землі проживало 7 млрд. осіб. Середньорічний приріст населення становить 2%, якщо  зміна кількості людей в країні за великий проміжок часу t описується формулою , де A- шукана величина,

A₀- відома кількість населення,

P- середньорічний приріст населення у відсотках,

t- розрахунковий термін.

2. Підготувати цікаві факти про відкриття Нобелівських лауреатів, що отримали премію за дослідження  з використанням показникової функції: П'єр Кюрі, Річардсон Оуен, Ігор Тамм, Луїс Альварес, Ганнес Альфвен, Роберт Вудро Вільсон.