Застосування логарифмічної функції в інших науках

Урок «Застосування логарифмічної функції в інших науках»

Тип уроку: урок узагальнення і систематизації знань.

 Мета: систематизувати і узагальнити знання і уміння учнів з теми «Логарифмічна функція»;

познайомитися з використанням логарифмічної функції  при розв'язанні прикладних задач;

навчитися використовувати метод проектів при дослідженні явищ навколишнього світу;

розвивати творче мислення, увагу, пам'ять, кмітливість, вміння працювати разом, культуру спілкування.

Обладнання: підручник з алгебри 11 клас автори МерзлякА.Г., Номіроввський Д.А., ПолонськийВ.Б., ЯкірМ.С., мультимедійна дошка, комп’ютер, картки для груп з дидактичним матеріалом, презентації, які виконані в Power Point, буклети, музичні твори – вальси Ф. Шопена.

ХІД УРОКУ

Перед початком уроку звучить вальс № 6 Ф.Шопена

І. Організаційний момент. Мотивація навчання

Підготовка учнів до уроку.

Сьогодні наш урок починається незвичайно, ми зустрічаємось з музичним твором Фредеріка Шопена. Чому так? На це питання відповідь отримаємо  на уроці. Ми будемо говорити на уроці математики про цікаві речі: музику, картини Сальвадора Далі, про зірки, про рослини, про закони, які керують всесвітом. Ми починаємо подорож до невідомого, розкриємо всі секрети логарифмічної функції. Тому  ідея уроку: «Щоб  дійти  до  мети, треба  перш  за  все  йти»(Оноре де Бальзак)

Зараз я кожному дарю посмішку -  Смайлік, нехай він допоможе вам в вашій праці на уроці. Сподіваюсь, ви надихаєте на нашу сумісну працю. Пропоную проговорити про себе наступні слова( слайд на екрані) 

- Я почуваю себе дуже впевнено

- Я вмію творчо мислити

- Мені подобається отримувати знання

- Я задоволений, що можу працювати на уроці

Актуалізація опорних знань.

Дидактична гра «Математичне лото»

Математика щедра, вона часто дає більше, ніж у неї просять

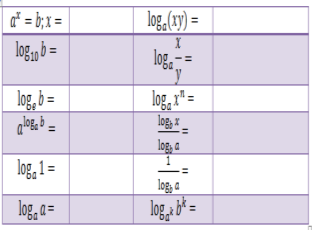
Завдання. Знайдіть продовження формули, сформулюйте правило  і заповніть порожні клітинки. Кожна група отримує картку, яку потрібно заповнити за 2 хвилини.

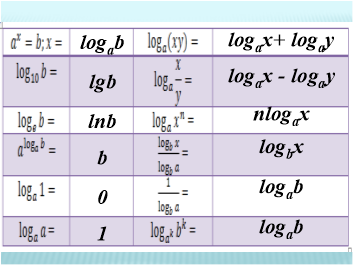Потім на інтерактивній дошці дається правильна відповідь. Учні роблять самоперевірку, виправляючи помилки на картках, потім здають їх вчителю.

Картка № 1

Аналіз опорних знань.  Сьогодні на уроці нам необхідно буде швидко знаходити значення логарифмів, тому почнемо з усної роботи. Обчисліть значення виразу (на екрані з’являються  приклади)

Нам також потрібно повторити методи розв’язування логарифмічних рівнянь.

 Самостійна робота у групах ( в групах по 3 учня, кожен розв’язує тільки одне рівняння) .

Картка № 2. Розв'яжіть рівняння

Завдання.

Серед заданих рівнянь назвіть ті, які не мають коренів, поясніть відповідь. ( Слайд на екрані, правильна відповідь - 1, 3, 4, 5, з’являється на екрані)

Захист міні-проекту групою істориків  «З історії логарифмів. Портретна галерея» - учнівська презентація.

До уроку вам було запропоновано творче завдання. Розглянемо розв’язання

Творче завдання. Число 7 представити за допомогою трьох цифр 2 та відомих вам математичних символів.

Розв’язання

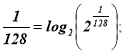
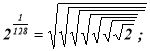
    Як представити число n за допомогою трьох цифр 2 та математичних символів?

Захист міні-проекту групою економістів «Логарифми в економіці» - розв’язання економічної задачі.

Задача. Відсоткова ставка дорівнює 16%, нарахування відсотків проводиться кожні півроку. Скільки треба часу, щоб початкова сума подвоїлась?

S=P(1+i)ⁿ, де n – кількість конверсійних періодів (загальна кількість нарахувань),     r  = 0,16 ,   m = 2. За умовою  S = 2P, отже отримали рівняння 2P = P(1+i)ⁿ,   можна   поділити   обидві   частини   рівняння   на  P, прологарифмуємо, тоді

ln2 = n ln(1+ i), i = r : m = 0,16 : 2, тому

Отже, початковий капітал подвоїтьсяприблизночерез9 конверсійнихперіодів, а саме через  t  = 9 : 2 = 4,5 року.

Подібні задачі можна розв’язувати у загальному вигляді для складених відсотків ,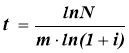

де  N – додатне число, яке показує кратність збільшення початкової суми;   t  - час (у роках),  r  - річна ставка (у відсотка),   m  - кількість нарахувань за рік;   i = r : m  – відсоткова ставка за конверсійний період.

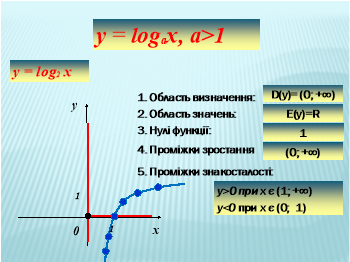
Повторимо теоретичний матеріал. Які властивості має логарифмічна функція?

Учні відповідають за схемою:

1. Область визначення.

2. Область значень.

3. Нулі функції.

4. Проміжки спадання.

5. Проміжки знакосталості.

Відповідає на питання один з учнів.

На слайді кожна властивість демонструється за допомогою анімації. Після відповіді учня на екрані з’являється  правильна відповідь.

Захист міні-проекту групою фізиків «Логарифми в фізиці»  - учнівська презентація.

Захист міні-проекту групою астрономів  «Логарифми в астрономії» - розв’язування задачі.

Задача. Знайдіть відстань до зірки Вега  α Ліри, якщо її видима та абсолютна зоряна величини 0,1 і 0,5.

m=0,1;   M=0,5;  M = m + 5 - 5 lg r;  де r – відстань до зорі, виміряна в парсеках.

lg r = (m + 5 - M ) : 5 = (0,1 + 5 -  0,5) : 5 = 0,92,  отже   r = 8,1 парсека(пк),

1 пк = 3,26 св.р. = 3 ∙ 10¹⁶ м,  тоді  r  = 2,43 ∙ 10¹⁷ м.

Відповідь:  відстань  до  зірки  Вега  2,43 ∙ 10¹⁷ м

Захист міні-проекту групою біологів  «Логарифмічна спіраль в біології»  - учнівська презентація та розв’язання задачі.

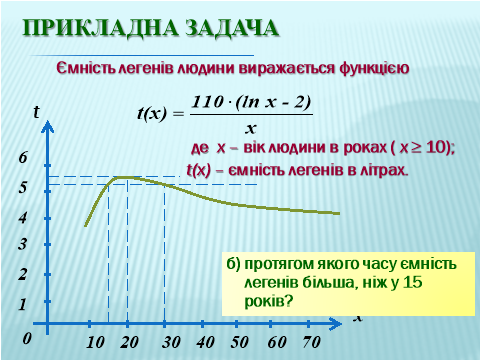
Задача. Ємність легенів людини виражається функцією   

де  х – вік людини в роках ( х ≥ 10);

t(x) – ємність легенів в літрах.

а) У якому віці ємність легенів людини максимальна і чому вона дорівнює?

Відповідь: в 20років ємкість легенів 5,7 л.

б) Протягом якого часу ємність легенів більша, ніж у 15 років?

Відповідь: з 15 по 30

років.

Захист міні-проекту групою музикантів  «Математика та музика - два полюси людської культури» - учнівська презентація.

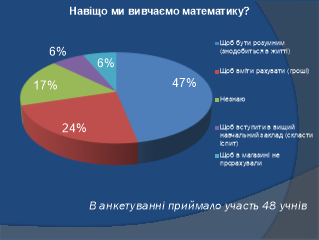
Захист міні-проекту групою журналістів  «Логарифми у художніх образах» - учнівська презентація, підсумки анкетування, ознайомлення з буклетом присутніх на уроці.

Підсумок уроку. «МУЗЫКА может возвышать душу,
ЖИВОПИСЬ  – радовать глаз,
ПОЭЗИЯ  -  пробуждать чувства,
ФИЛОСОФИЯ  – удовлетворять потребности разума,
ИНЖЕНЕРНОЕ  ДЕЛО – совершенствовать материальную сторону жизни людей, а МАТЕМАТИКА  способна  достичь  всех  этих  целей», -  так казав американський математик Моріс Клайн.

Порівняйте свої знання на початку і в кінці уроку і дайте відповіді на запитання: Мікрофон

• Чи отримав ти задоволення від власної праці?
• Який етап уроку був найцікавішим?
• Які загальнонавчальні вміння допомагали тебе?
• На розвиток яких якостей, здібностей, рис характеру вплинув цей урок? (мислення, пам’яті, уваги, самостійності, спостережливості тощо.)
• В якому настрої ви перебували на уроці?
• Щось заважало вам працювати продуктивно?
• Чи можемо сказати, що цей урок важливий для вас?

Зробимо підсумок нашої проектної діяльності. Ми побудували проект «Чи потрібно вивчати логарифми?». У проекті було використано багато цікавого матеріалу, розв’язані задачі з різних наук, практичного змісту. У процесі роботи над проектом ви спостерігали застосування ваших знань для розв’язання проблем. Ми довели собі, що без математики неможлива успішна діяльність людини.

Оцінювання роботи груп, учнів.

Домашнє завдання. Обов'язкова частина   №

Додаткове завдання   №

Рефлексія. Якщо ти отримав задоволення від власної праці,тобі була зрозуміла більша частина матеріалу, то пропоную створити на дошці зі Смайліків сонечко. Так ми поєднаємось до наступної спільної праці. Закінчуємо урок вальсом Шопена, тепер ми знаємо, що поєднує математику та музику.