Урок засвоєння знань "Визначений інтеграл"

Тема: Визначений інтеграл.

 

Мета уроку:

Дидактична мета: поглибити й розширити знання учнів про визначений інтеграл; закріпити навички знаходити визначений інтеграл, показати його місце і значення при розв’язуванні задач фізичного, економічного, геометричного змісту; учити бачити єдину математичну модель у різних ситуаціях, складати її в нестандартних умовах; вчити учнів досліджувати й оцінювати соціальні явища засобами математики; бачити необхідність планування майбутнього; допомогти сформувати особисте ставлення до діяльності, яка вимагає математичних знань.

Розвиваюча мета: формувати вміння виступати перед аудиторією, чітко формулювати і відстоювати свою думку; розвивати спостережливість, логічне мислення, інтелектуальні здібності учнів; сприяти розширенню їх кругозору; розвивати фізико-математичну мову учнів.

Виховна мета: виховувати патріотичні почуття, інтерес до науки шляхом звернення до історичних джерел, вміння раціонально використовувати робочий час.

Тип уроку: урок систематизації знань, вмінь та навичок.

Обладнання: навчальний клас, дошка, комп’ютер, презентація в редакторі PowerPoint.

 

ДЕВІЗ УРОКУ: «Світ, що нас оточує – це світ інтегрального і диференціального числення. Тож давайте його пізнавати» Х. Гюйгенс

 

ХІД УРОКУ

 

І. ОРГАНІЗАЦІЙНИЙ МОМЕНТ

Добрий день. Щоб розпочати урок ми з вами зробимо гімнастику для розуму, скажіть мені, будь-ласка, слова які ми вивчили в останньому розділі на уроках алгебри та яку він мав назву.

 

ІІ. МОТИВАЦІЯ НАВЧАЛЬНОЇ ДІЯЛЬНОСТІ

Ми з вами сьогодні спробуємо за допомогою математики розв’язати проблеми, що виникають на уроках фізики, економіки та інших сфер діяльності людини. До речі, задача (англ. problem) означає «проблема».

Проблема розв’язування задач ускладнюється в тому випадку, якщо вміння побачити єдину математичну модель у різних ситуаціях недостатньо розвинене. Можливість розвивати ці уміння ви й матимете сьогодні, розв’язуючи задачі, пов’язані з геометрією, фізичними явищами, економічними процесами. І ви матимете чудову нагоду закріпити і розвинути навички знаходити визначений інтеграл, застосовувати його при розв’язуванні практичних задач.

Отже, відкрили зошити, записали дату і тему уроку «Визначений інтеграл»

ІІІ. ПЕРЕВІРКА ДОМАШНЬОГО ЗАВДАННЯ

 

IV. АКТУАЛІЗАЦІЯ ОПОРНИХ ЗНАНЬ

Фронтальне опитування із завданнями

1. Що називають первісною даної функції?

Первісною для функції f(x) називається така функція F(x), похідна якої F’(x) дорівнює f(x).

 

VІ. Систематизація знань

Для того, щоб розпочати доводити, що математика використовується в усіх галузях науки ми спочатку запишемо щ:

1. Що є невизначеним інтегралом? Це функція.
2. Що є визначеним інтегралом? Визначений – число.

Девізом нашого уроку будуть слова голландського вченого Х. Гюйгенса «Світ, що нас оточує – це світ інтегрального і диференціального числення.

Тож давайте його пізнавати».

Запишемо формулу Ньютона – Лейбніца.

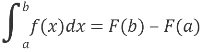
Приклад:

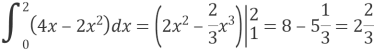
Виконати №519.

Поняття інтеграла – важливе як у шкільному курсі математики, так і в курсі вищої математики, що розгалужується на низку цікавих, хоч і складних, математичних дисциплін. Назву вам лише кілька з них: математичний аналіз, функціональний аналіз, теорія функції комплексної змінної, диференціальні рівняння, теорія ймовірностей, теорія оптимізації математичних процесів.

Окрім математичних, є науки, що широко використовують математичний апарат і нині дуже популярні, оскільки необхідні для ведення різноманітних справ, для гармонійного розвитку галузей виробництва, тощо. У цих науках також використовується поняття інтеграла. Серед них такі як:

економіка виробництва,

фінансова справа,

електроніка,

програмування,

фізика,

хімія,

радіофізика, тощо.

Давайте з’ясуємо, як саме ми можемо застосувати визначений інтеграл в таких науках, як геометрія, фізика, економіка.

А зараз, панове, давайте перенесемося в майбутнє, років на 20 вперед.

Ви – дорослі, солідні люди, знайшли своє місце в житті: конструктори,

інженери, металурги, будівельники, економісти, плановики, вчені. І в процесі своєї роботи ви зустрічаєтеся з різними проблемами, які вам необхідно вирішити.

Ми попередньо розбилися на групи, кожна з яких отримала певне

завдання і зараз по черзі ви будите звітувати про виконану роботу. А всі останні групи будуть оцінювати вашу роботу.

 

І група «Економісти»

Нашій групі було запропонована економіка. Економіка – одна з найскладніших галузей діяльності. Але економіка най більш пов’язана з математикою. Економічні об’єкти можуть бути описані сотнями, тисячами

параметрів, багато з яких носять випадковий характер. Крім того, в економіці

присутній людський фактор. Передбачити поведінку людини часом буває

важко, а іноді взагалі неможливо. Економіка залежить від соціального впорядкування суспільства, від політики і ще від багатьох факторів. І все ж моделювання економічних явищ, об’єктів, процесів є можливим завдяки математичній операції інтегрування. Ми знайшли одну з най важливіших задач, особливо для підприємців малого бізнесу.

Задача 1.

Відомо, що попит на деякий товар задається функцією p = 4 - q , де q -

кількість товару (у шт.), p - ціна одиниці товару, а рівновага на ринку даного

товару досягається при p* = q* = 1. Визначите споживчого надлишку (SG).

Розв’язання:

Відповідь: споживчий надлишок дорівнює .

 

ІІ група «Фінансисти»

Задача 2.

На полі пшениці після приземлення космічного корабля залишився слід, який нагадує фігуру, обмежену лініями у = х² – 2х та у = 3. Необхідно визначити збитки, завдані агрокомплексом, якщо з 1 м отримують в середньому 3,8 кг пшениці, яка коштує 0,8 грн./кг.

Розв’язання:

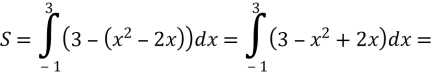
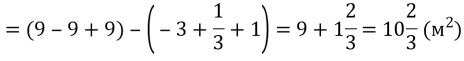
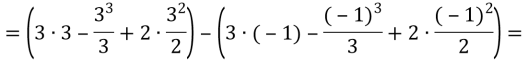
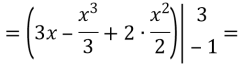
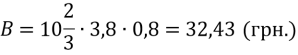
Здавалось з такої населеної ділянки, але втрати достатньо великі.

 

ІІІ група «Біологи та екологи»

Певну суму знань про закономірності розвитку природи, взаємодію

суспільства і природного середовища, про проблеми й завдання його охорони

та збереження учні дістають, розв’язуючи задачі біологічного та екологічного змістів.

Загальновідомо, що найпростішою функціональною залежністю між

двома змінними величинами х та у є лінійна залежність y=kx+b, де ; k та b ‒

параметри.

У біології лінійна залежність між двома змінними зустрічається досить рідко. Проте за певних умов залежність між двома змінними інколи можна описати лінійною функцією.

Задача 3.

Знайти площу пелюстка ромашки, який розміщено між дугами парабол , .

Розв’язання:

Дана фігура обмежена графіками двох функцій: , .

Шукана площа за допомогою інтеграла обчислюється так:

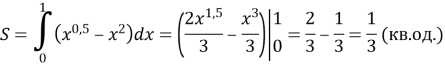
Відповідь. кв. од.

 

ІV група «Енергетики»

Задача 4.

Навантаження на Криворізьку теплоелектростанцію задається функцією f(x) = 3x + 4x – 2. Визначити витрати електроенергії протягом доби.

Розв’язання:

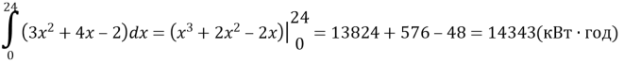
Відповідь: 14343 кВт·год.

 

V група «Хіміки»

У хімії теж багато задач розв’язується за допомогою інтегрування. – приріст кількості речовини, яка вступила в хімічну реакцію за проміжок часу [τ ;τ ].

Застосувавши поняття інтеграла приходять до висновку: кількість хімічної речовини m, яка вступила в хімічну реакцію за проміжок часу [τ ;τ ] дорівнює:

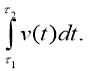
Задача 5.

Швидкість зміни концентрації речовини, що вступила в реакцію, виражається функцією v = 3t + 1, де t – час (с), v – швидкість (моль/с×м ). Як зміниться концентрація речовини за час t =0 до t =5 c?

Розв’язання:

Задача розв’язується методом безпосереднього інтегрування. Оскільки v(t)=C`(t) ,то C(t) – концентрація речовини і первісна для v(t), тому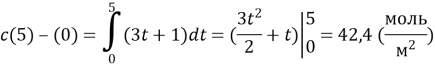

Наведені приклади ‒ це лише невелика частинка того, як математичне моделювання допомагає показати життєву необхідність знань, а таких прикладів можна привести ще дуже багато.

Розв’язання прикладних задач сприяє створенню в учнів піднесеного емоційного настрою, активності в навчанні, формуванню практичних умінь і навичок, необхідних у повсякденному дорослому житті.

 

VІІ. Підведення підсумків уроку.

Тестування.

Рефлексія:

Скажіть, будь ласка, що саме ми з вами робили сьогодні на уроці?

(розв’язували задачі з геометрії, фізики, економіки, перекладали

мовою математики проблеми, які стоять перед іншими науками.)

На сьогоднішньому уроці ми ще раз переконалися в тому, що математичні теорії є надійним знаряддям в розкритті таємниць природи, законів економічних процесів.

Звертаю вашу увагу, шановні добродії, на програмові вимоги та підборку завдань для підготовки до незалежного зовнішнього тестування, поміщену у вашому Кроці до майстерності з даної теми.

 

VІІІ. Домашнє завдання.

§15 №525

 

 

 

Додаток 1

I варіант

1. Первісна для у=cos x є:

А) sin x               Б) cos x+C         В) sin x+C             Г)  - sin x+C

2. Первісна для у= а^х є:

А) а^х +С             Б) а^х                    В) +C             Г)   а^х ln a+C

3. Первісна для у=x^α є:

А) αх^α-1+C          Б)               В) +C            Г)   +C, α≠-1

4. Первісна для у= є:

А) +С            Б) x+C                В) 2+C             Г) -2+C

5. Первісна існує для функцій

А) парних          Б) непарних      В) зростаючих     Г)  неперервних на <а;в>

6. Невизначений інтеграл – це

А) множина первісних виду f(x) +C              Б) множина первісних виду F'(x) +C     

В) множина первісних виду f '(x) +C            Г)  множина первісних виду F(x) +C

7. Геометричною інтерпретацією визначеного інтеграла є:

А) площа криволінійної трапеції на      Б) об’єм тіла обертання на

В) довжина кривої на                              Г)  робота тіла на

8. дорівнює:

А) ln 3              Б) ln 5                    В) 5                      Г) 0

9.

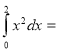
А) 4                      Б) 2                В) 8                       Г)2

 

 

II варіант

1. Первісна для у =sin x є:

А.  cos х + С         Б. sin x              В. – соsх + С         Г. sіn х + С

2. Первісна для у = є:

А. + С               Б. + С            В. + С          Г. + С

3. Первісна для у = е є:

А. е                      Б. + С           В. + С            Г. е + С

4. Первісна для у = є:

 А. lnx + C            Б. + C             В.  ln + С           Г. + C

5.  Множина первісних для f (x) має вид:

 А. f (x) + С         Б. F(x) + C           В. F'(x) + С            Г. f '(x) + С

6. Визначений інтеграл це:

А. множина первісних виду F(x) + C             Б. границя інтегральних сум на

В. границя відношення приросту функції до приросту аргументу  Г. множина первісних f '(x) + С

7. Фізичним змістом визначеного інтеграла є:

 А. площа криволінійної трапеції         Б. об’єм тіла обертання на

 В. робота тіла на                                    Г. шлях, пройдений на

8. дорівнює:

А.  27                   Б.  27ln3                В.                         Г. 81

9.

А.  1                     Б.  1                    В.  3                       Г.  – 1 

 

Додаток 2

Відповіді тестів

1 варіант

1	2	3	4	5	6	7	8	9
В	В	Г	В	Г	Г	А	А	Б

 

2 варіант

1	2	3	4	5	6	7	8	9
В	Г	А	В	Б	Б	А	В	Б