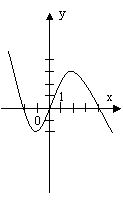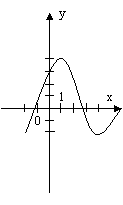Уроки "Квадратична функція".

Розробка уроків з теми: «Квадратична функція» (9 клас)                                                                             вчителя математики загальноосвітнього НВК №4 м. Бердичева Рудої Людмили Миколаївни

Система навчальних занять
з теми „Квадратична функція”.

 

Тема вивчається в 9-му класі з поглибленим
вивченням математики в І семестрі.

 

Урок №1-2.

 

Урок з теми: Квадратична функція, її графік та властивості.

 

Мета: Розширити відомості про квадратичну функцію: сформувати навички побудови графіка; вміння формулювати властивості функції; застосовувати властивості функції до розв’язування задач; розвивати графічні навички.

 

Тип уроку: Урок формування і вдосконалення вмінь та навичок.

 

Обладнання: Заготовлені системи координат (на ватмані).

 

Орієнтовний план і методи проведення уроку.

 

1. Представлення теми та очікуваних результатів уроку. (бесіда до 2 хв.)
2. Актуалізація опорних знань та вмінь. (технологія „Мікрофон”) (10 хв.)
3. Пояснення нового матеріалу (15 хв.)
4. Формування нових умінь і навичок (робота в групах). (10 хв. + 1 хв. на звіт)
5. Оцінювання результатів уроку.

 

Хід уроку.

 

І. Учитель повідомляє учням, що математика вивчає оточуючий світ за допомогою абстрактних моделей, в яких реальні величини замінюють математичними поняттями. Значна роль належить поняттю функції. Квадратична функція саме та, яка частіше інших використовується в будівництві та архітектурі, тому сьогодні на уроці перед нами поставлено завдання – розширити відомості про квадратичну функцію.

 

ІІ. Актуалізація опорних знань.

 

У даній ситуації використовую інтерактивну технологію „Мікрофон”. „Мікрофон” надає можливість усім сказати (в даному випадку вказати властивості заданої графічно функції), по черзі висловлюючи свою думку.

Правила проведення цієї форми такі:

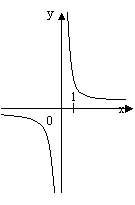
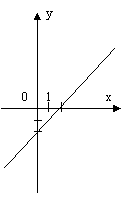
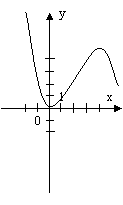
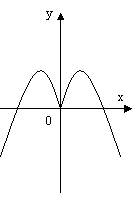
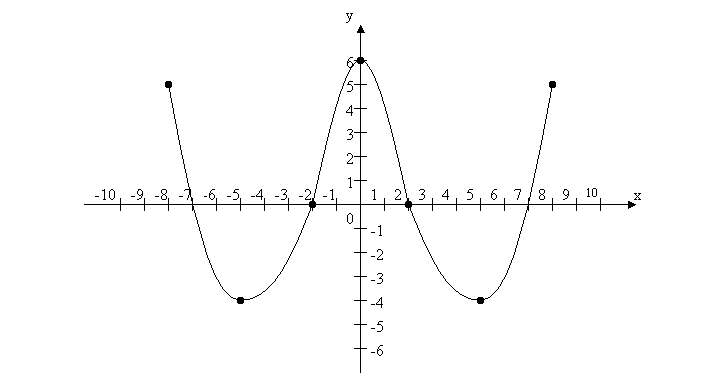
• учням пропонується побудований графік функції (малюнок №1), по якому потрібно визначити:

а) область визначення функції;

б) область значень функції;

в) найбільше, найменше значення функції;

г) перевірити функцію на парність, непарність;

д) нулі функції;

е) проміжки зростання і спадання функції;

є) проміжки знакосталості функції.

мал. 1

 

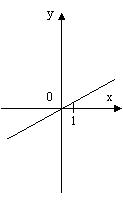
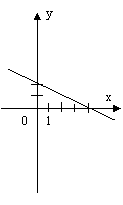
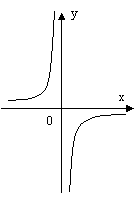
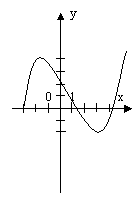
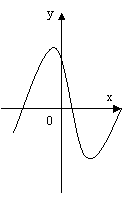
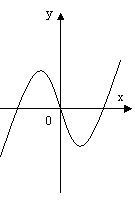
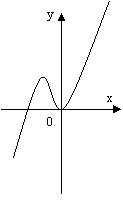
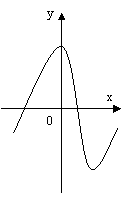
На малюнку 2 зображені графіки функцій, задані формулами. Учням пропонуються функціональні залежності. Для кожної функції вказати відповідний графік, назвати координати вершини параболи.

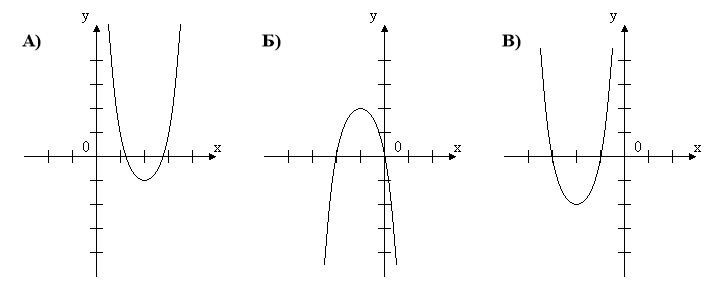
мал. 2

 

Функціональні залежності: у = (х + 2)² – 2; у = (х – 2)² – 1; у = -(х + 1)² + 2.

 

 

 

 

Методика проведення інтерактивної технології „Мікрофон”:

• учням пропонується один предмет (ручку, олівець), якщо виконувати роль уявного мікрофона. Учні самі передаватимуть його один одному, по черзі беручи слово, тобто обираючи собі питання з яким на їхню думку, вони найкраще справляться;
• учитель не втручається ні в процес передачі символічного мікрофона, ні у вибір завдання;
• коли хтось висловлюється, інші не мають права його переривати, щось говорити або підказувати;
• можна запропонувати учням самим оцінити свої відповіді;
• процес триватиме, поки не будуть розв’язані всі завдання.

 

Відповіді до запропонованих завдань.

 

Малюнок №1

 

а) х є [-8; 8];

б) х є [-4; 6];

в) y_max = 6; y_min = -4;

г) функція парна;

д) х₁ = -7; х₂ = -2; х₃ = 2; х₄ = 7;

е) f(x)↑, x є [-5; 0] U [5; 8];

    f(x)↓, x є [-8; -5] U [0; 5];

є) y > 0, x є (-8; -7) U (-2; 2) U (7; 8);

    y < 0, x є (-7; -2) U (2; 7).

 

Малюнок №2

 

а) у = (х – 2)² – 1; б) у = -(х + 1)² + 2; в) у = (х + 2)² – 2.

  (2; -1) ;   (-1; 2) ;   (-2; -2).

 

ІІІ. Виклад нового матеріалу.

 

Запишемо загальний вигляд квадратичної функції у = ах² + bх + c.

Виділимо із тричлена ax² + bx + c повний квадрат (можна викликати учня до дошки).

 

 

 

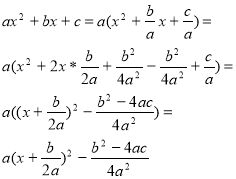
Ми отримали вже відому формулу вигляду у = а(x – m)² + n, де m = ;

n = .

Значить, графіком функції у = ах² + bx + c є парабола, вершиною якої є точка
(m; n), де m = ; n = .

Віссю симетрії є пряма x = m, паралельна до осі ординат.

При a > 0 гілки напрямлені вгору;

при a < 0 – вниз.

 

Алгоритм побудови графіка
квадратичної функції.

 

1. Знаходимо вершину параболи і проводимо вісь симетрії.
2. Обчислюємо нулі функції.
3. Будуємо декілька допоміжних точок (для точності побудови графіка).

 

Наприклад: y = x² – 5x + 6

 

1. m = 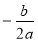= = 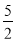2,5;

n = 2,5² – 5 * 2,5 + 6 = -0,25.

Вершина має координати (2,5; - 0,25).

 

2. Знаходимо нулі функції:

x² – 5x + 6 = 0

x₁ = 2; x₂ = 3.   (2; 0); (3; 0)

 

3. Знайдемо координати точки перетину графіка з віссю ординат.

(0; 6)

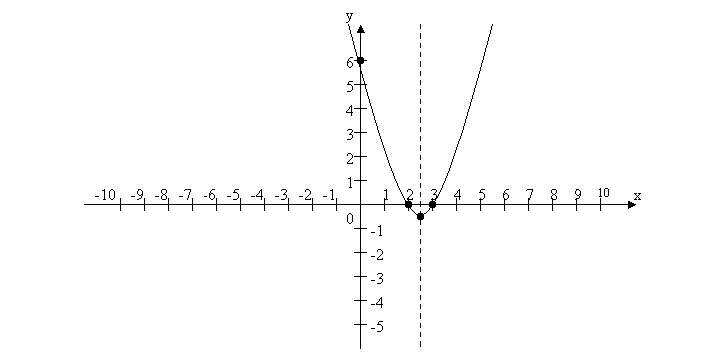
Властивості:

1. x є R;
2. y_min = -0,25
3. f(x)↑   x є [2,5; +∞)

f(x)↓   x є (-∞; 2,5]

4. f(x) > 0 x є (-∞; 2)U(3; +∞)

f(x) < 0 x є (2; 3)

 

ІV. Організація діяльності учнів для закріплення нового матеріалу. (робота в групах – розсажені на початку уроку).

 

Кожна група отримує картку із завданням, в якому потрібно дослідити квадратичну функцію, побудувати графік і описати властивості. (графік зображується на заготовленій системі координат).

 

Рекомендовані завдання:

 

1. у = 0,5х² + 3х + 0,5
2. у = -х² + 2х + 8
3. у = х² – 4х + 7
4. у = -2х² – 5х – 2

 

V. Підведення підсумків і оцінювання результатів роботи.

 

Наступний урок (продовження).

 

Підтема: Застосування знань по темі „квадратична функція” до розв’язування вправ.

 

Тип уроку: Урок закріплення та застосування знань, умінь та навичок.

 

Хід уроку.

 

І. Робота біля дошки.

 

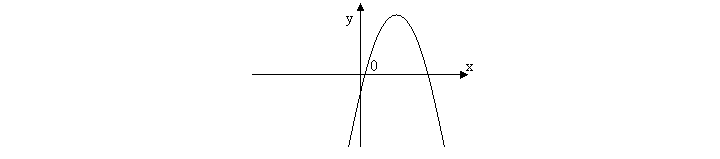
1. За видом графіка функції y = ax² + bx + c визначте знаки коефіцієнтів a, b, c. Оберіть правильне твердження.

 

 

 

А		Б		В		Г		Д
	a > 0 b > 0 c > 0		a > 0 b < 0 c > 0		a > 0 b < 0 c > 0		a < 0 b < 0 c < 0		a < 0 b > 0 c < 0

 

Розв’язання.

 

1.        a < 0 (гілки параболи, напрямлені вниз)
2.        Знайдемо нулі функції.

ax² + bx + c = 0 | : a

x² + x + = 0

За теоремою Вієта x₁* x₂ =

x₁ * x₂ > 0 (по графіку)

> 0 с < 0 або  x = 0; y = c < 0 (по графіку)

3.        x₁ + x₂ = -

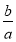
x₁ + x₂ > 0 (по графіку)

- > 0 < 0 b > 0

Відповідь: Д.

 

2. Парабола, що є графіком квадратичної функції y = ax² + bx + c, має верщину в точці М (2; 1) і проходить через точку К (-1; 5). Знайти значення коефіцієнтів a, b і с.

Розв’язання.

Запишемо формули знаходження координат вершини параболи.

m = - = 2; n = = 1

Складаємо систему трьох рівнянь.

 

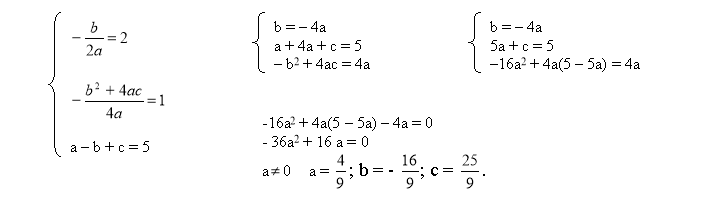
ІІ. Інтерактивна технологія „Мозаїка”.

 

Методика проведення технології „Мозаїка”:

а) клас ділиться умовно на групи залежно від того, якого кольору картку він витягне;

б) заздалегідь готуються картки різного кольору з написаними на них завданнями;

в) кожна картка має не тільки свій колір, а й номер.

г) група разом розв’язує свої завдання, можлива допомога вчителя;

д) коли завдання розв’язані, утворюються нові групи (за номерами). Всі перші номери – це одна група, учні з картками №2 – це друга група і т. д.

е) відбувається спілкування в новій групі, кожен учень розказує про свої завдання, навчає інших, записи ведуться на картках;

є) коли роботу закінчено, учні повертаються в попередні групи (за кольором) і обговорюють почуте;

ж) підводиться підсумок уроку.

 

Червоні картки:

Сині картки:

 

1. Побудувати графік функції f(x) = x² – 4x + 3. Користуючись графіком, знайти проміжки знакосталості.
2. При яких значеннях p і q графік функції проходить через точки А(1; -1) і
   В (3; -2)?
3. При яких значеннях а функція y = 3x² – 12x + a набуває додатніх значень при всіх дійсних значеннях х?

 

Жовті картки:

 

1. Побудувати графік функції f(x) = 6x – 3x². Користуючись графіком функції вказати проміжки зростання, спадання функції.
2. Графік квадратичної функції – парабола з вершиною в точці С(0; 4), що проходить через точку D(-5; -46). Задати цю функцію формулою.
3. При яких значеннях а функція y = (a + 5)x² – 4x + 2 набуває від’ємних значень при всіх дійсних значеннях х?

 

Білі картки:

 

1. Побудувати графік функції y = 4x – 2x². Користуючись графіком знайти:

а) f(-1); f(3).

б) значення х, при яких f(x) = 2; f(x) = 3; f(x) = -6.

2. Побудувати в одній системі координат графіки функцій y = x² + x – 2 і y = 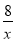. Користуючись малюнком, знайти корені рівняння x² + x – 2 = .
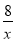3. При якому значенні а графік квадратичної функції y = ax² + (a – 4)x – 4,5 дотикається осі абсцис?

 

ІІІ. Підведення підсумків, оцінювання результатів уроку.

 

Учні повідомляють, чому навчилися на уроці. Учитель орієнтує учнів на практичне застосування теми на наступному уроці.

 

ІV. Домашнє завдання.

 

Збірник (А. Т. Мерзляк, В. Б. Полонський, Е. М. Рабінович, М. С. Якір)

Стор. 113  №89; 92; 97; 102.

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Урок №3.

Урок з теми: Застосування властивостей квадратичної функції в будівництві та архітектурі.

 

Мета: Формування вмінь та навичок використання властивостей квадратичної функції в практичній діяльності людини. Розвиток творчих здібностей учнів. Вироблення вмінь знаходити математичні закономірності в навколишньому світі.

 

Обладнання: Калькулятор, таблиці з умовами задач, дидактичні матеріали.

 

Форма проведення уроку: Урок-практикум.

 

Тип уроку: Урок закріплення та застосування знань, вмінь, навичок.

 

Епіграф уроку: „Математика й техніка впливають на наше духовне життя і настільки, що ми рідко можемо це уявити собі повністю”.

Ван дер Варден Барти Лендерт

(голландський математик ХХ ст.)

 

Хід уроку.

 

І. Мотивація навчальної діяльності учнів. Повідомлення теми, мети, завдань уроку.

 

Ще у 1931р. видатний математик, механік, кораблебудівник Олексій Миколайович Крилов (1863-1945) писав: „Тепер математика так проникла в техніку всіх галузей будівельної справи, всіх галузей машинобудування, суднобудування, побудови літальних апаратів, артилерійської справи, електротехніки, оптики й ін., що не можна собі й уявити жодної споруди, яку не було б попередньо розраховано”.

У практичній діяльності людини математика має велике значення як прикладна наука, зокрема в будівництві та архітектурі.

Багато розрахункових задач цих галузей зводяться до розв’язування квадратних рівнянь, нерівностей, використання властивостей квадратичної функції. Сьогодні на уроці ми розглядаємо практичне застосування властивостей квадратичної функції в будівництві та архітектурі, будемо продовжувати шукати математичні закономірності в навколишньому світі.

 

ІІ. Актуалізація опорних знань.

 

а) Фронтальна бесіда.

1) Сформулюйте означення квадратичної функції.

2) Як називається графік квадратичної функції?

3) Який напрям мають вітки параболи залежно від значень коефіцієнта а?

4) Якою формулою можна задати функцію, графік якої зображено на малюнку 1.

 

 

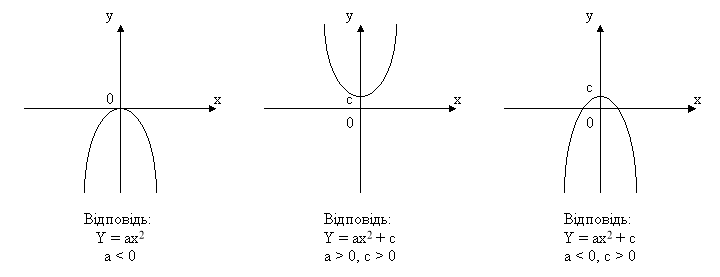
мал. 1

б) Усні вправи.

1) Графік квадратичної функції – парабола з вершиною в початку координат, що проходить через точку А (6; -3). Задати цю функцію формулою.

2) Графік квадратичної функції – парабола з вершиною в точці С (0; 4), що проходить через точку D(5; 54). Задати цю функцію формулою.

 

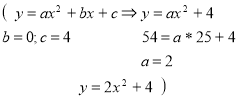
ІІІ. Розв’язування творчих завдань.

 

Задача №1.

 

На малюнку 2 зображено міст, опорна арка якого має форму параболи. Скласти рівняння цієї параболи, якщо висота арки H = 5 м. і найбільша ширина її L = 20 м.

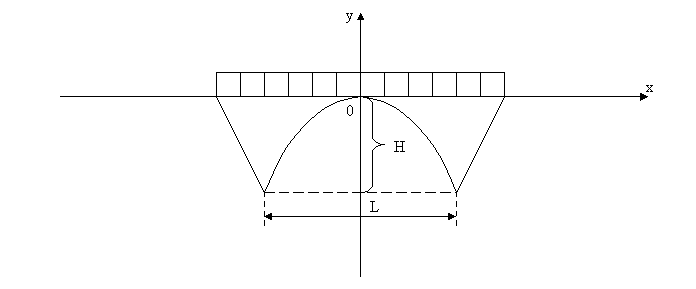
мал. 2

 

Колективне обговорення.

• Як можна вибрати систему координат?
• Виберемо осі координат так, щоб вісь ОХ пройшла вздовж моста, а вісь ОY – по осі симетрії параболи.
• Який вигляд у цій системі координат має рівняння параболи?
• Рівняння параболи має вигляд y = ax², де a < 0
• На який відстані від осі симетрії параболи знаходиться точка А?

(20 : 2 = 10 м)

• Знайти координати точки А

А(10; -5)

• Графіку якої функції належить точка А?

y = ax²

• Яка рівність справедлива в цьому випадку?

-5 = a * 10²

a = = - 0,05

• Який вигляд має рівняння параболи?

y = -0,05х²

 

Задача №2.

 

Ланцюги, які підтримують міст, що вісить, мають форму параболи ACB
(малюнок 3). Кінці ланцюгів закріплено в точках A і B на опорах AA' і ВВ' висотою 30 м. Довжина прогону А'В' = 200 м. Найменша висота ланцюгів над мостом ОС = 5 м. Знайти довжини підвісних тросів (вертикальних стержнів, що з’єднують міст з ланцюгами), якщо відомо, що вони розташовані на однаковій відстані один від одного.

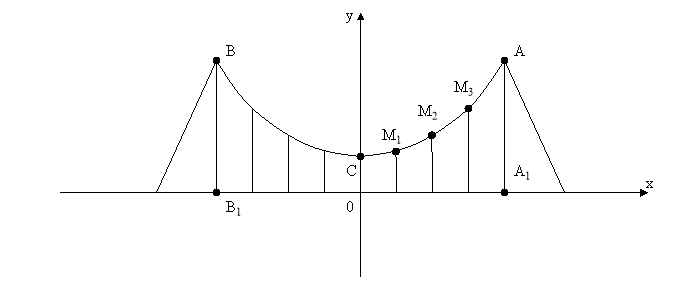
мал. 3

 

Учні колективно розв’язують задачу.

Виберемо систему координат так, щоб вісь ОХ пройшла вздовж моста, вісь ОY – по осі симетрії параболи. Тоді парабола буде графіком квадратичної функції y = ax² + c,
а > 0. Довжини підвісних тросів відповідатимуть ординатам точок М₁, М₂, М₃ параболи. Знайдемо коефіцієнти а і с. Вершиною параболи є точка С (0; 5) (за умовою ОС = 5 м)
с = 5.

Знайдемо координати точки А.

А'В' = 200 (м), ОА' = 200 * = 100 (м), АА₁ = 30 м, А (100; 30). Точка А належить параболі. Підставимо координати точки А (100; 30) в рівняння y = ax² + 5

30 = a * 100² + 5 a = 0,0025

Рівняння параболи y = 0,0025x² + 5

Абсциси точок М₁, М₂, М₃ дорівнюють відповідно, x₁ = = 25; x₂ = 25 * 2 = 50; x₃ = 25 * 3 = 75, отже, ордината точки М₁ дорівнює: y₁ = 0,0025 * 25² + 5 6,56 (м)

  y₂ = 0,0025 * 50² + 5 = 11,25 (м)

  у₃ = 0,0025 * 75² + 5 19,06 (м)

Відповідь: 6,56 м; 11,25 м; 19,06 м.

 

ІV. Практична робота під керівництвом учителя.

 

Учні діляться на дві групи.

До першої групи входять учні, які планують виконати завдання самостійно, до другої – учні, які будуть виконувати задачу за даним алгоритмом.

 

Завдання.

 

На малюнку 4 зображена мостова форма, у якої лінія АСВ – дуга параболи з вершиною С. Довжина прогону АВ = 84 м, ОС = 12 м; прогін поділено на 6 рівних частин. Знайти довжини вертикальних стояків форми.

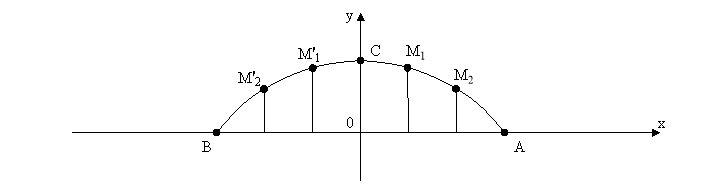
мал. 4

 

Алгоритм розв’язування задачі.

1. Виберіть осі координат.
2. Напишіть рівняння параболи в обраній системі координат.

(y = ах² + с, а < 0, с = 12, y = ах² + 12).

3. Знайдіть координати вершини параболи. (С(0; 12))
4. Обчисліть ОА (ОА = ОВ = 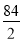= 42 м)
5. Знайдіть координати точки (А(42; 0))
6. Обчисліть значення коефіцієнта а, підставивши в рівняння з n 2 координати точки А.

(0 = а * 42² + 12, а = ).

7. Запишіть рівняння параболи.

(у = х² + 12)

8. Знайдіть ординату точки М₁, підставивши в рівняння параболи її абсцису.

(у₁ = * 14² + 12; у₁ = 10,67).

9. Знайдіть координати точки М₂.

(х₂ = 14 * 2 = 28; у = * 28² + 12 6,67 м).

 

V. Домашнє завдання.

 

Збірник (Мерзляк, Полянський, Якір).

 

VІ. Підбиття підсумків.

 

„Сьогодні на уроці ми застосували набуті знання з математики в практичній діяльності, використовували властивості квадратичної функції в архітектурі та будівництві. Ми ще раз упевнилися в тому, що математичні знання необхідні в нашому житті на кожному кроці”.

 

 

Урок №4.

 

Урок з теми: Побудова графіків функцій, що містять знак модуля.

 

Мета:

• Повторити основні поняття: функція, область визначення, нулі функції, властивості функцій: парність, непарність, монотонність. Формувати вміння та навички побудови графіків функцій, що містять знак модуля.
• Розвивати пізнавальний інтерес учнів; логічне мислення; надавати можливість „стати успішним”.
• Виховувати самостійне мислення, увагу та зосередженість.

 

Тип уроку: Урок вивчення нового матеріалу.

 

Форма проведення уроку: Урок-лекція.

 

Тривалість заняття: 1 урок (45 хв.)

 

Наочність: Варіанти тестових завдань.

 

Учні повинні знати: означення функції, область визначення функції, властивості (парність, непарність, монотонність); теоретичний матеріал щодо побудови графіків, які містять знак модуля.

 

Учні набуватимуть навички: застосування розглянутого матеріалу до побудови графіків функцій.

 

План уроку.

 

1. Організаційний момент.
2. Повторення вивчених теоретичних положень (тестові завдання).
3. Пояснення нового матеріалу у вигляді лекції.
4. Розв’язування вправ.
5. Підбиття підсумків уроку.
6. Домашнє завдання.

 

Хід уроку.

 

І. Організаційний момент.

 

Учні отримують аркуш паперу із заготовленими завданнями. Учитель називає час, який відводиться на виконання завдань. (12 хвилин).

 

ІІ. Повторення вивчених теоретичних положень у вигляді тестових завдань.
(4 варіанта).

 

Тестові завдання 1-10 містять по п’ять варіантів відповідей, з яких тільки одна – правильна.

1. Серед наведених графіків укажіть графік функції y = 2 -

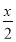
А	Б	В	Г	Д

 

2. Задано функцію формулою g(x) = 2x - 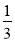x².

Знайти g(-3)

А	Б	В	Г	Д
-3	-9	-8	8	інша відповідь

 

3. При якому значенні x значення функції f(x) = 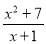дорівнює 4.

А	Б	В	Г	Д
3 і 4	3	3 і 1	1	інша відповідь

 

4. Знайти область визначення функції.

f(x) =

А	Б	В	Г	Д
(-4; 4)	[4; +∞)	(4; +∞)	(-∞; 4]	(-∞; 4)

 

5. Укажіть малюнок, на якому функція, що задана графіком, зростає на проміжку [0; 4]

А	Б	В	Г	Д

 

6. Знайти, не виконуючи побудови, точки перетину графіка з віссю абсцис.
   y = x² – 4x + 3

А	Б	В	Г	Д
(1; 0) і (3; 0)	(-1; 0)	(0; 3)	(1; 3)	інша відповідь

 

7. Укажіть малюнок, на якому зображено графік парної функції.

А	Б	В	Г	Д

 

8. Знайти, не виконуючи побудови графіка нулі функції. Y = 6x – 2x²

А	Б	В	Г	Д
(0; 0)	(0; 3)	(3; 0)	(0; 0); (3; 0)	інша відповідь

 

9. Графік квадратичної функції – парабола з вершиною в точці А(0; -5), що проходить через точку В(4; 27). Задати цю функцію.

А	Б	В	Г	Д
y = x2 – 5	y = 2x2 – 5	y = 2x2 + 5	y = x2 + 5	інша відповідь

 

10.  На параболі y = -x² + 5x + 5 знайти точку, у якої абсциса і ордината рівні.

А	Б	В	Г	Д
(-1; -1)	(-5; -5)	(-1; -1); (-5; -5)	(-1; -5)	інша відповідь

 

ІІІ. Оголошення теми уроку.

 

„Побудова графіків функцій, що містять знак модуля”.

 

IV. Пояснення нового матеріалу.

 

Матеріал викладаю лекційним методом із складанням таблиці. Учні ділять зошит на дві частини. В першій записують правило, за яким будується графік, в другій – самостійно виконується завдання. Через 1-2 хвилини учень або учитель пропонує правильну відповідь. Учні отримують додаткові бали, які додаються до балів, одержаних під час тестування.

 

 

№ п/п	Правило (говорить учитель)	Графік (самостійно)
1.	Щоб побудувати графік функції y = f(|x|), потрібно побудувати графік функції f(x) для х ≥ 0 і отриманий графік симетрично відобразити відносно осі „OY”.
2.	Щоб побудувати графік функції y = |f(x)| потрібно побудувати графік функції y = f(x) і та частина графіка, яка над віссю „OX” залишається без змін, а та частина графіка, яка під віссю „OX” відображається відноно осі „OX”.
3.	Щоб побудувати графік функції y = |f(|x|)| потрібно побудувати графік функції f(x), слідуючий f(x), і в кінці y = |f(x)|.
4.	Щоб побудувати графік функції |y| = f(x) спочатку будуємо графік y = f(x) і та частина графіка, яка розміщена під віссю OX відкидаєтья, а та яка над віссю OX симетрично відображається відносно осі OX.
5.	Щоб побудувати графік залежності |y| = f(|x|) спочатку будуємо графік f(|x|), а потім |y| = f(|x|) (див. п. №4)
6.	Щоб побудувати графік функції |y| = |f(x)|, спочатку будуємо y = |f(x)| і отриманий графік симетрично відображаємо відносно осі OX.
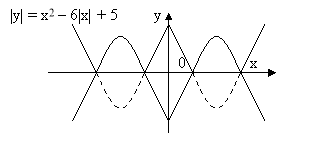
7.	Побудова графіка функції |y| = |f(|x|)|. (Самостійне дослідження).	|y| = |x2 – 6|x| + 5|

V. Розв’язування вправ.

 

Побудувати графіки функцій.

1) y = |-x² + 6x - 8|

2) |y| = x² – 5x + 6

3) y = -x² + 4|x| – 5

4) |y| = |-x² + 4x - 5|

 

VI. Підбиття підсумків уроку.

 

Якщо при поясненні нового матеріалу учні пропонували правильні відповіді, то отримані бали додаються до балів, отриманих за тестові завдання. Підрахувати кількість балів можна після перевірки тестів.

 

VIІ. Домашнє завдання.

 

1. Побудувати графіки функцій.

А) у = |3x + 5|

Б) |y| = 3x + 5

В) |y| = x² + 4|x| – 8

 

2. Знайти область визначення функції

А) у =

Б) Збірник (Мерзляк, Полонський, Якір)

 

Урок №5-6.

 

Урок з теми: Функції. Властивості функцій. Перетворення графіків функцій.

 

Мета:

• Повторити, узагальнити і систематизувати основні поняття: функція, графік функції, область визначення і область значень функції, нулі функції, проміжки знакосталості; властивості функцій: парність і непарність, монотонність; основні елементарні функції: лінійна, пряма і обернена пропорційність, квадратична функція, степенева з натуральним показником. Повторити побудови і перетворення графіків функцій.
• Розвивати пам’ять, логічне та критичне мислення учнів, вміння пояснювати свої дії.
• Виховувати наполегливість, увагу та зосередженість, самостійне мислення, уміння працювати в групі.

 

Учні повинні знати: означення функції, область визначення і область значень функції, властивості функції (парність і непарність, монотонність), основні елементарні функції, їх графіки і властивості, правила перетворення і побудови графіків функцій.

 

Учні повинні вміти: знаходити область визначення, область значень, нулі функції, проміжки знакосталості і монотонності, будувати графіки функцій.

 

Учні набуватимуть навики: застосування властивостей функцій до побудови графіків функцій.

 

Тип уроку: узагальнення та систематизація знань.

 

Форма проведення уроку: гра „Математичне лото”.

 

Тривалість заняття: 2 уроки (90 хв.)

 

Наочність: конверти із завданнями.

 

Епіграф уроку: „Математика цікава тоді, коли дає поживу нашій винахідливості й здатності до міркувань”.

Д. Пойа.

 

Організація гри.

 

Для кожної з п’яти команд необхідно заздалегідь приготувати по два цупкі аркуші паперу, щоб на одному з них (лише з одного боку) був кольоровий малюнок, на фоні якого зображена система координат з побудованим графіком функції. Ці аркуші потрібно розкреслити на 25 рівних частин. На одному аркуші (основі) кожна картинка нумерується і у ній записуються завдання, а на іншому листі (з малюнком) на чистій стороні – відповіді до цих завдань. Цей другий лист розрізається на прямокутники, фрагменти малюнка змішуються, формуються п’ять пакетів по п’ять карток у кожному. Окрім цього для кожної команди ще слід підготувати третій цупкий лист паперу, про роль якого скажу пізніше. Важливо, щоб кожний пакет і картки у ньому мали свій порядковий номер.

1	6	11	16	21
2	7	12	17	22
3	8	13	18	23
4	9	14	19	24
5	10	15	20	25

Це основа, у клітинках якої записані завдання. (зворотній бік листа чистий).

У клітинах цього листа записані відповіді. На звороті малюнок.

 

До цього уроку учні мають повторити весь теоретичний матеріал з даної теми, а також переглянути всі практичні завдання, які вони виконували по темі.

 

Хід уроку.

 

І. Організаційний етап. Оголошення теми і мети уроку.

 

Учні займають місця по периметру класу. В центрі класу – „ігрові столи”. Вчитель оголошує тему уроку. Метою уроку є підготовка до контрольної роботи.

 

ІІ. Повторення, узагальнення і систематизація основних теоретичних положень
(І тур гри).

 

У І турі беруть участь усі учні класу. Учитель виводить на екран запитання і зачитує його. Учень, який першим правильно відповідає на нього, стає учасником ІІ туру. Учні, які відповіли на першу п’ятірку запитань, потрапляють до різних груп і т. д. Якщо на чергове запитання не знає правильної відповіді жоден з учнів, що залишилися, то повторне право відповіді має учень, що вже потрапив до ІІ туру. У разі правильної відповіді він може надати право участі у ІІ турі своєму однокласнику і, якщо є вільне місце, зарахувати його до своєї команди. Таким чином набирається п’ять команд по п’ять осіб у кожній. Оскільки першими відповідають, як правило, найкраще підготовлені учні, то в результаті утворюються гетерогенні групи. Бажання надати місце у своїй команді друзям буде стимулювати активність учнів, які вже потрапили до ІІ туру. Решта стають помічниками учителя: з них призначаються п’ять спостерігачів (по одному на кожну команду) і два-три ведучих гри.

 

 

 

Завдання І туру.

 

1. Сформулювати означення функції.

 

2. Що називається областю визначення функції?

 

3. Що називається областю функції?

 

4. Що називається графіком функції?

 

5. Що є графіком лінійної функції, прямої, оберненої пропорційності,
   функції y = x²; y = ax² + bx + c?

 

6. Що таке нулі функції? Що таке проміжки знакосталості?

 

7. Як, не виконуючи побудови знайти координати точок перетину графіка з осями координат?

 

8. Як, не виконуючи побудови, знайти координати точки перетину графіків функцій y = f(x) і y = g(x)?

 

9. Дати означення функції, яка зростає на проміжку. Навести приклад зростаючої лінійної функції.

 

10. Дати означення функції, яка спадає на проміжку. Навести приклад спадної лінійної функції.

 

11. Яка функція називається парною? Яка властивість графіка парної функції?

 

12. Яка функція називається непарною? Яка властивість графіка непарної функції?

 

13. Чи завжди функція є парною або непарною? Що можна сказати про графік функції, яка є ні парною, ні непарною?

 

14. Яку функцію називають квадратичною?

 

15. Що є графіком квадратичної функції? Як залежить розміщення графіка в залежності від числа а?

 

16. За якими формулами обчислюються координати вершини параболи?

 

17. Як за відомим графіком функції y = f(x) побудувати графік функції y = f(-x)?

 

18. Як за відомим графіком функції y = f(x) побудувати графік функції  y = -f(x)?

 

19. Як за відомим графіком функції y = f(x) побудувати графік функції
    y = f(x + a)?

 

20. Як за відомим графіком функції y = f(x) побудувати графік функції
    y = f(x) + b?

 

21. Як за відомим графіком функції y = f(x) побудувати графік функції y = f(kx)?

 

22. Як за відомим графіком функції y = f(x) побудувати графік функції y = f(|x|)?

 

23. Як за відомим графіком функції y = f(x) побудувати графік функції y = |f(x)|?

 

24. Як за відомим графіком функції y = f(x) побудувати графік функції |y| = f(x)?

 

25. Як за відомим графіком функції y = f(x) побудувати графік функції |y| = |f(x)|?

 

ІІІ. Вироблення вмінь та навичок (ІІ тур гри).

 

Один із ведучих зачитує одне завдання командам (заготовлені на дошці під час першого туру). (інші завдання закриті). Учні – члени команд – уважно слухають, при потребі письмово розв’язують завдання. Відповідь міститься на картці тільки одного (!) із членів кожної команди. Тоді цю картку віддають спостерігачеві, який повинен її покласти на відповідну клітинку таблиці – основи кольоровою стороною до нього, а відповіддю – назовні. Якщо одночасно у кількох членів однієї команди знайшлася картка з „правильною” відповіддю (що неможливо!), то вони мають право на обговорення (до звукового сигналу). Коли один з учасників обговорення переконав команду у своїй правоті, то він віддає спостерігачеві свою картку. Якщо ж під час обговорення учасники групи не прийшли до спільної думки, то відповідна клітинка таблиці залишається порожньою і команда втрачає шанси на перемогу. Так, ведучі зачитують всі 25 завдань, а таблиці кожної команди поступово вкривають картки з відповідями. Тоді спостерігач кожної команди накриває таблицю третім аркушем і обережно перевертає все на інший бік.

 

Завдання ІІ туру.

 

1. Для функції y = – 4x² + 5 знайти f(-2) та f(0,5) [-11; 4].

 

2. Для функції y = – 2x – 3 знайти х, при якому f(x) = 0 та f(x) = -5 [-1,5; 1].

 

3. Областю визначення якої функції є проміжок (-∞; 0)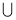(0; +∞)? [y = ].

 

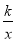4. Областю визначення якої функції є проміжок [0; +∞)? [y = ].

 

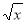5. Знайти область значень функції y = x² + 1 та y = (x + 3)² + 1 [y є [1; +∞)].

 

6. Знайти найбільше значення функції y = -2x² та y = -(x – 5)² [y = 0].

 

7. Знайти координати вершини графіка функції y = x² – 6x + 5 [(3; -4)].

 

8. Функції f(x) і g(x) – непарні і f(-5) = 2; g(2) = -5. Обчислити -2f(5) + 3g(-2) [19].

 

9. Функція f(x) – парна, g(x) – непарна, і f(-7) = -11; g(5) = -2. Обчислити
   f(-7) – 3g(-5) [-17].

 

10. Знайти координати точок перетину графіків функцій: y = 2x² + 7x – 4 та
    y = x – 4 [(-3; 7); (0,5; 0)]

 

11. Знайти координати точок перетину графіків функцій: y = x² – 6 та y = x – 4
    [(2; -2); (-1; -5)].

 

12. Знайти координати точок перетину графіків функцій: y = 2x – x² та y = -2x
    [(0; 0); (4; -8)].

 

13. Розв’язати графічно рівняння x² = 2 – x [x = 1].

 

14. Знайти область визначення функції y = 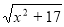[x є R].

 

15. Знайти область визначення функції y = 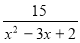[x є (-∞; 1)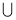(1; 2)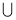(2; +∞)]

 

16. Знайти область визначення функції y =
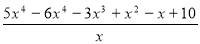
    [x є (-∞; 0)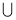(0;+∞)]

 

17. Знайти область визначення функції y = 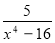[x є (-∞; -2)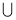(-2; 2)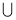(2; +∞)].

 

18. Знайти область визначення функції y =
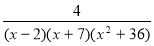
    [x є (-∞; -7)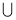(-7; -2)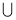(2; +∞)].

 

19. Перевірити функцію на парність, непарність. f(x) = 6x⁶ – 5x² [парна].

 

20. Перевірити функцію на парність, непарність f(x) = [непарна].

 

21. Перевірити функцію на парність, непарність f(x) = x⁴ – x [ні парна ні непарна].

 

22. Знайти проміжки, на яких f(x) > 0, якщо f(x) = x² – 2x – 3
    [x є (-∞; -1)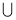(3; +∞)].

 

23. Знайти проміжки, на яких f(x) < 0, якщо f(x) = 6x – 2x² [(0; 3)].

 

24. Побудувати графік функції y = .

 

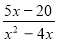25. Задати формулою лінійну функцію, графік якої паралельний прямій
    y = 2 – 4x і проходить через точку M(-3; 5) [y = -4x – 7]

 

ІV. Розв’язування творчих вправ. (ІІІ тур гри – супергра)

 

Якщо зняти верхню основу, то всі побачать п’ять чудових кольорових картин, на тлі яких зображена система координат, в якій побудовано графік функції (за умови, що всі учасники команд правильно розв’язали завдання). В третьому турі командам пропонується розшифрувати цей графік. Кожній команді пропонується аналітичний вигляд відповідної функції.

 

І команда: y = (|x| – 1)² + 1

 

 

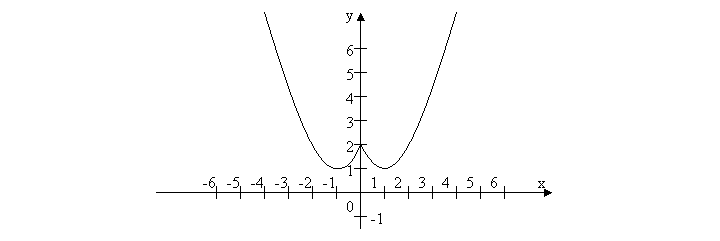
ІІ команда: y = 2 –

 

 

ІІІ команда: y = |2 – |

 

 

 

 

 

 

ІV команда: y = |x² – |x| – 6|

 

 

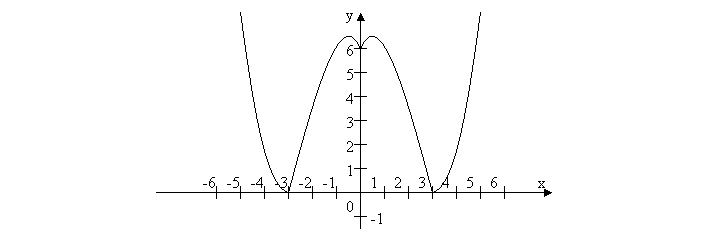
V команда: |y| = |x² – 7x + 10|

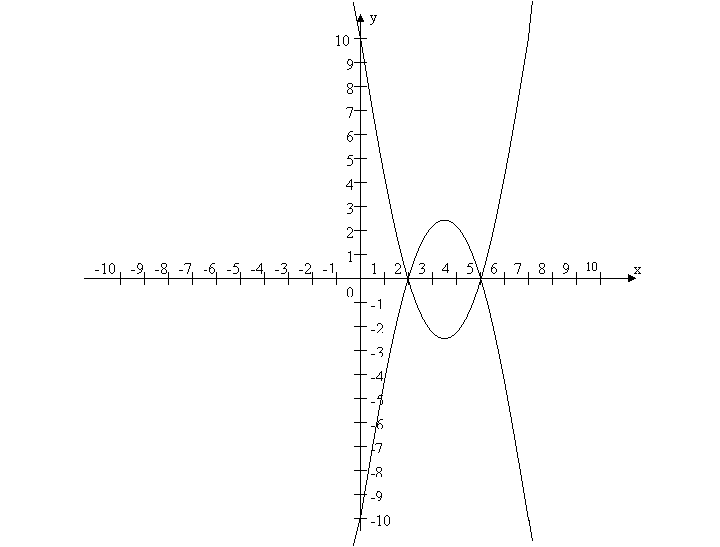
V. Підбиття підсумків.

 

Спостерігачі знімають верхню основу і під контролем учителя оцінюють результати гри. Якщо картина складена правильно, то всі члени команди мають по 10 балів. Якщо ж є помилка, то це легко виявити за карткою. Та картка, що псує зображення, вилучається. Картка пронумерована, а отже, відомий учасник гри, що припустився помилки. За це йому знижується оцінка. За порожні клітинки знижується оцінка всім гравцям команди. Якщо команда правильно побудувала графік, то всім гравцям додається по 2 бали. Підраховується сума балів для кожної з команд і оголошуються переможці гри. Вчитель виставляє оцінки відповідно до результатів кожного учасника гри.

 

VІ. Домашнє завдання.

 

№1. Знайти область визначення функції.

а) f(x) = ;

б) y = .

 

№2. Чи є парною або непарною функція, задана формулою.

а) y = ;

б) y = x⁷ – 3x⁵.

 

№3. Побудувати графіки функцій.

а) y = (x + 2)² – 1

б) y = ;

в) y = ||.