уроки по темі "Вологість"

Рекомендації до вивчення теми: «Насичена пара. Абсолютна і відносна вологість».

Під час вивчення програмного матеріалу пов’язаного з вологістю повітря учні порівняно легко засвоюють методику знаходження абсолютної і відносної вологості, вміння користуватися психрометричною таблицею.  Однак при вивченні теми “Вологість повітря”, в учнів виникають певні труднощі з розумінням процесів пов’язаних з переходом ненасиченої пари в насичену а також із процесами зміну стану насиченої пари. Зрозуміти учням ці особливості дозволить розв’язання спеціально підібраних задач.

Перед тим як приступити до розв’язання задач, з учнями потрібно ще раз узагальнити і дати чітке означення основних понять. 

Внаслідок руху молекул рідини деякі молекули набувають енергії достатньої щоб перемогти силу притягання до молекул рідини і вириваються із її поверхні. Над поверхнею рідини може знаходитися будь-який газ. Ми зупинимося на розгляді явища переходу молекул із поверхні води в повітря. В відкритій посудині молекули води будуть вириватися із її поверхні і заповнювати повітряний простір над посудиною (атмосферу Землі). Так як повітряна оболонка Землі порівняно з посудиною надзвичайно велика, то процес випаровування буде тривати до того часу, доки вся вода не випарується. В цьому випадку пара води над посудиною є ненасиченою (кількість молекул, що вириваються з поверхні води більша за кількість, що повертаються назад в воду).

Якщо посудину з водою закрити, то молекули, що вилетіли з поверхні води, не будуть розсіюватися в повітряному просторі Землі. Через деякий час встановиться так звана динамічна рівновага між водою і водяною парою, яка знаходиться в посудині над поверхнею рідини. Найбільший тиск (пружність) пари, яка насичує простір над рідиною при даній температурі, тобто перебуває з нею в стані динамічної рівноваги, при якій за одиницю часу випаровується стільки ж рідини, скільки конденсується пари, називається тиском насиченої пари. Густина насиченої пари також є максимальною для даної температури. Тиск і густина насиченої пари збільшується при підвищенні температури. Особливо потрібно наголосити що тиск насиченої водяної пари є постійним для певного значення температури і не залежить від об’єму посудини.

Величина тиску і густина насиченої пари при певній температурі подана в таблиці 1. При бажанні можна проаналізувати з учнями значення тиску насиченої пари в залежності від температури для інших рідин (Таблиця 4), а також проаналізувати значення тиску водяної пари при температурах вищих за 100ºС (Таблиця 2) і нижчих зо 0ºС (льодом) (Таблиця 3).

Необхідно звернути особливу увагу учнів на те, що “вологе” повітря над поверхнею води складається з “сухого” повітря і водяної пари. Тому тиск над поверхнею зумовлений сумою парціальних тисків “сухого” повітря і тиску водяної пари. Ці відмінності насиченої водяної пари, не дозволяють використовувати газові закони без врахування можливого переходу пари в насичений стан, з подальшим переходом насиченої пари в рідину. Усвідомити суть і особливості цих процесів і допоможе розв’язання учнями наступних задач.

Задача 1.

    Температура водяної пари 29ºС і тиск 23 мм рт.ст. Як слід змінити об’єм пари, щоб вона стала насиченою?

t = 29ºC                       В таблиці 1 знаходимо значення тиску насиченої  P₁ = 23 мм рт.ст.       пари  при температурі 29ºС.

                                    Р₂ = Р_нас(29_ºС) = 30 мм рт.ст.

V₂/V₁ - ?                      Так як температура пари залишається постійною то можна скористатися законом Бойля-Маріотта.

P₁·V₁ = P₂·V₂ .

Звідси: V₂/V₁ = Р₁/Р₂. V₂/V₁ = 23/30 = 0,77. Відповідь. Водяну пару потрібно стиснути до 0,77 початкового об’єму.

 

   Задача 2.

У приміщенні, температура якого 22ºС, міститься 1 г пари, тиск якої 6,6 мм рт.ст. Скільки потрібно додати води в це приміщення, щоб пара стала насиченою?

t = 22ºC                      Знаходимо в таблиці 1 густину насиченої пари при m = 1 г                        температурі 22ºС.    ρ_нас = 19,83 г/м³ = 0,01983 кг/м³. Р = 6,6 мм рт.ст.        З рівняння Менделеєва-Клапейрона знайдемо                                     об’єм пари яка міститься в приміщенні: Δm - ?                          V = (m·R·T)/(M·P). Густина пари, яка міститься в приміщенні, рівна:   ρ = m/V.

Маса водяної пари (густина), яку потрібно додатково випарувати, в одиницю об’єму рівна:  Δρ = ρ_нас – ρ = ρ_нас - m/V.

Загальна маса води, яку потрібно випарувати, в усьому приміщенні рівна:      m = Δρ·V = (ρ_нас – m/V)·V = ρ_нас·V – m = ρ_нас. (m·R·T)/(M·P) – m. Виразимо всі величини в одиницях СІ і проведемо обчислення. m = 1г = 0,001кг,      Р = 6,6 мм рт.ст. = 6,6·133 Па = 877,8 Па,      R = 8,31 Дж/(моль·К), Т = 273 + 22 =295 К,  М(Н₂О) = 18·10^-3 кг/моль.

m = 0,01983·0,001·8,31·295/(18·10^-3·877,8) – 0,001 = 0,00016·295/16 – 0,001 = 0,0485/16 – 0,001 = 0,003 – 0,001 = 0,002 (кг) = 2 г.

Відповідь. Щоб пара в приміщенні стала насиченою потрібно випарувати 2 г води.

Виведення остаточної формули в загальному вигляді і остаточний числовий підрахунок, як видно із прикладу розв’язання попередньої задачі, є досить громіздким. Тому розв’язання задач такого типу набагато зручніше виконувати поетапно з виконанням проміжних обчислень. Це дає змогу зразу оцінювати послідовність подальшого виконання обчислень. Потрібно також враховувати доцільність переходу до одиниць СІ (якщо користуємося позасистемними одиницями, то пишемо ці одиниці при підстановці в формулу, разом із числовим значенням).

 

Задача 3. 

У посудині міститься водяна пара при температурі 30ºС і тиску 20 мм рт.ст. Чи стане пара насиченою, якщо посудину охолодити до 22ºС?

 

 

t₁ = 30ºC                        Пара в посудині ненасичена, тому для знаходження P₁ = 20 мм рт.ст.          тиску після охолодження скористаємося законом t₂ = 22ºC                        Шарля:   Р₂/Р₁ = Т₂/Т₁. Звідси  Р₂ = (Р₁·Т₂)/Т₁.

                                       Т₁ = 273 + 30 =303 К, Р₂ - ?                              Т₂ = 273 + 22 = 295 К.

                                            Р₂ = (20 мм рт.ст.·295)/303 = 5900 мм рт.ст./303 =

= 19,47 мм рт.ст.

 Тиск насиченої пари при температурі 22ºС знаходимо в таблиці 1:  Р_{нас(22ºС)} = 19,83 мм рт.ст.

Тиск пари після охолодження менший ніж тиск насиченої пари. 

Р2 < Р_{нас(22ºС)}.

Відповідь. Пара не стане насиченою.      Задача 4.

Температура в кімнаті 18ºС, а тиск водяної пари 7,8 мм рт.ст. У металевий чайник налили холодної води. При якій температурі чайник перестане пітніти? 

Розв’язання. Чайник перестане пітніти, тоді коли температура води (точка роси) стане більшою за температуру, при якій тиск пари буде рівний насиченій парі тобто 7,8 мм рт.ст. З таблиці знаходимо, що такому тиску відповідає температура 8ºС (беремо найближче більше значення температури наведене в таблиці).

Відповідь. Чайник перестане пітніти коли вода в ньому нагріється до 8ºС.

       Задача 5.

Ненасичена водяна пара масою 0,276 г зазнає ізотермічного стискання. Коли об’єм пари зменшився до 12 л, почалася її конденсація. При якій температурі відбувався процес? m = 0,276 г        Конденсація пари розпочинається якщо пара стає насиченою. V = 12 л             Так як процес стискання пари ізотермічний, то температура  t₁  = t₂ = t            при якій здійснювався процес стискання рівна температурі                             при якій пара стає насиченою.

t - ?                      Знайдемо густину насиченої водяної пари: ρ_нас = m/v. V = 12 л = 12·10^-3м³. ρ_нас = 0,276 г/(12 10^-3м³) = 23 г/м³. В таблиці знаходимо що дана густина насиченої водяної пари відповідає температурі 25ºС.

Відповідь. Процес відбувався при температурі 25ºС.

Задача 6.

У циліндрі під поршнем ізотермічно стискають 0,90 г водяної пари при температурі 29ºС. Який буде об’єм пари, коли почнеться конденсація? m = 0,90 г            В таблиці знаходимо густину насиченої пари при t₁  = t₂ = 29ºС      температурі 29ºС.    ρ_нас = 28,7 г/м³.

                             З формули ρ_нас = m/V₂, знаходимо V₂.

V₂ - ?                    V₂ = m/ρ_нас ;       V₂ = 0,9 г/(28,7 г/м³) = 0,03 м³. Відповідь. Об’єм пари буде 0,03 м³.

При розв’язуванні задач, в яких відбувається перехід ненасиченої пари із одного стану в другий, потрібно з’ясувати чи залишиться пара в другому стані ненасиченою чи стане насиченою. Для цього потрібно порівняти густину (пружність) яку має пара в першому стані із густиною (пружністю) насиченої пари в другому стані. Якщо пара залишається ненасиченою то для опису змін стану можна користуватися газовими законами. При переході ненасиченої пари в насичену потрібно встановити за яких параметрів це відбувається, і до досягнення цих значень користуватися газовими законами, а після враховувати що в посудині є і насичена пара (тиск якої постійний) і вода.

Задача 7.

У закритому балоні міститься насичена водяна пара (без води) при температурі 100ºС. Який буде тиск пари, якщо балон нагріти до 120ºС?

 

t₁ = 100ºС         В таблиці знаходимо тиск насиченої водяної пари при t₂ = 120ºС температурі 100ºС.    Р₁ = Р_нас = 760 мм рт.ст. V₁ = V₂               Так як в балоні міститься лише водяна пара, то                            перехід із одного стану в інший описується законом 

Р₂ - ?                  Шарля:   Р₂/Р₁ = Т₂/Т₁.   Звідси: Р₂ = Р₁·Т₂/Т₁.

 

Т₁ = 273 + 100 =373 К;      Т₂ = 273 + 120 = 393 К.

Р₂ =760 мм рт.ст.·393/373 = 298680 мм рт.ст./373 ≈ 801 мм рт.ст.

Тиск насиченої пари при 120ºС 1473 мм рт.ст. Отже пара в балоні стала ненасиченою, використання закону Шарля є правильним.

Відповідь. Тиск пари стане рівним 801 мм рт.ст..

Задача 8. Тиск водяної пари при температурі 15ºС 1280 Н/м², об’єм 5,76 л. Який буде тиск пари, якщо температура підвищиться до 27ºС, а об’єм збільшиться до 8,0 л?

Для визначення тиску скористаємося рівнянням стану: 

t₁ = 15ºC    (Р₁·V₁)/Т₁ = (Р₂·V₂)/Т₂. Звідси отримаємо: Р₁ = 1280 Н/м²        Р₂ = (Р₁·V₁·Т₂)/(V₂·Т₁).

V₁ = 5,76 л Т₁ = 273 + 15 = 288 К;         Т₂ = 273 + 27 = 300 К. t₂ = 27ºC Р₂ = (1280·5,76 л·300)/(8,0 л·288) = (7372,8·300)/2304 = V₂ =8,0 л = 2211840/2304 = 960 (Па).

 Знайдемо в таблиці яким повинен бути тиск пари при Р₂ - ? температурі 27ºС щоб пара була насиченою:

Р₂ = Р_нас = 26,74 мм рт.ст. = 3556 Па.

Пара при переході із першого стану в другий залишилася ненасиченою. Отже використання рівняння стану при розв’язанні задачі є правильним. Відповідь. Тиск пари стане рівним 960 Па.

          Задача 9.

Водяну пару при температурі 40ºС і тиску 1117 Н/м² охолодили ізохорним процесом до 7ºС. Визначити тиск пари. t1 = 40ºC         Для визначення тиску пари після охолодження скористаємося законом Шарля: Р₁/Т₁ = Р₂/Т_2. Звідси:

Р₁ = 1117 Н/м₂             Р² = (Р₁·Т₂)/Т₁.

^{t2 = 7ºC}                         Т₁ = 273 + 40 =313 К;     Т² = 273 + 7 = 280 К.

^{V1 = V2}                         Р2 = (1117·280)/313 = 312760/313 = 999,75 Па.

 

Р₂ - ?   Знайдемо в таблиці тиск насиченої водяної пари при температурі 7ºС.   Р_нас(7ºС) = 7,5 мм рт.ст. = 

= 7,5·133,3 Па = 999,75 Па.

Відповідь. Після охолодження пара стане насиченою і

її тиск буде рівним 999,75 Па ≈ 1000 Па.

       Задача 10. Об’єм водяної пари при температурі 100ºС і тиску 190 мм рт.ст. зменшено ізотермічним процесом у 12 раз. В якому стані буде пара?

t₁ = 100ºC Знайдемо можливий кінцевий тиск після зменшення об’єму в 12 раз, скориставшись законом Бойля-

Р₁ = 190 мм рт.ст. t₁ = t₂         Маріотта:   Р1·V1 = Р2·V2; звідки  Р2 = Р1·(V1/V2). V₁ = 12·V₂          Р2 = 190 мм рт.ст.·(12·V2/V2) = 190 мм рт.ст.·12 =

 = 2280 мм рт.ст.

Р - ?                             В таблиці знайдемо тиск насиченої пари при 100ºС. 

Р_нас(100ºС) = 760 мм рт.ст. Як бачимо обчислений тиск

більший ніж тиск насиченої пари при 100ºС. Отже пара стане насиченою при стисканні меншому ніж в 12 раз.

Знайдемо в скільки разів потрібно стиснути пару з початкового стану щоб вона стала насиченою. Для цього скористуємося законом Бойля-Маріотта взявши за кінцевий тиск тиск насиченої пари при 100ºС. 

Р_нас/Р₁ = 760 мм рт.ст./190 мм рт.ст. = 4 (рази). 

При подальшому стисканні тиск пари буде залишатися постійним. Пара буде конденсуватися в воду. Щоб досягнути зменшення об’єму в 12 раз то потрібно ще додатково зменшити об’єм вже насиченої водяної пари ще в три рази. Це означає що 2/3 маси пари перетвориться в воду, тому що маса насиченої (після 4-кратного стискання) пари дорівнює масі ненасиченої пари.

Відповідь. 2/3 всієї пари перетвориться в воду, а тиск буде рівним 760 мм рт.ст.

Тиск у посудині в якій знаходиться пара і повітря зумовлений сумою парціальних тисків сухого повітря і пари. При зміні стану вологого повітря для ненасиченої пари і сухого повітря можна користуватися газовими законами.

        Задача 11. У посудині при температурі 20ºС і тиску 760 мм рт.ст. міститься повітря, насичене водяною парою. Який тиск сухого повітря в цій посудині? Який буде тиск повітря, насиченого водяною парою, якщо об’єм зменшити в 2 рази, а температура буде така сама?

t₁ = 20ºC                               Тиск в посудині зумовлений тиском сухого повітря  Р₁ = 760 мм рт.ст.               і водяної пари. t1 = t2 Р1 = Р_{1 сух.повітря} + Р_пари.

V₁ = 2·V₂ Знайдемо в таблиці тиск насиченої пари при                                              температурі 20ºС. Р_пари = 17,54 мм рт.ст.

Р2 - ?                              Р_{1сух.повітря} = Р1 - Р_пари = 760 мм рт.ст. – 17,54 мм.рт.ст. = = 742,46 мм рт.ст.

При зменшенні об’єму тиск насиченої пари залишиться постійним. Тиск сухого повітря після зменшення об’єму визначимо за законом Бойля-

Маріотта.         Р1сух.повітря·V1 = Р2сух.повітря·V2.   

Звідси:    Р2сух.повітря = (Р1сух.повітря·V1)/V2.   Р2сух.повітря = (742,46 мм рт.ст.·2·V₂)/V₂ = 1484,92 мм рт.ст.

Тоді:       Р2 = Р_{2сух.повітря} + Р_пари ;          Р2 = 1484,92 мм рт.ст. + 17,54 мм рт.ст. = = 1502,46 мм рт.ст.

      Відповідь. Початковий тиск сухого повітря 742,46 мм рт.ст. Кінцевий тиск вологого повітря 1502,46 мм рт.ст.

 

          Задача 12

Тиск повітря, насиченого водяною парою, 76 см рт.ст. Якщо об’єм повітря зменшити в три рази, його тиск буде 222 см рт.ст. Визначити тиск і температуру пари, вважаючи процес ізотермічним.

Р₁ = 76 см рт.ст. Тиск повітря дорівнює сумі тиску сухого повітря і Р₂ = 222 см рт.ст.          тиску пари, який залишається постійним тому що t₁ = t₂ = t                          пара насичена.

     V₁ = 3·V₂ Р₁ = Р_{1 сух.повітря} + Р_пари.    (1)

Р₂ = Р_{2 сух.повітря} + Р_пари       (2)

Р_пари - ?  t - ?                   Процес стиснення повітря можна описати законом

Бойля-Маріотта.   Р1сух.повітря·V1 = Р2сух.повітря·V2.  

Звідси: Р1сух.повітря = (Р2сух.повітря·V2)/V1 = Р2сух.повітря·(V2/V1) = Р2сух.повітря·(1/3)

=

= (Р2сух.повітря)/3.

Підставимо отримане значення Р_{1сух.повітря} в рівняння (1).

Р1 = (Р2сух.повітря)/3 + Рпари    (3)

Визначимо Р2сух.повітря   з рівняння (3).

Р2сух.повітря = 3Р1 - 3Рпари  .      

Підставимо отримане значення в (2). Отримаємо:

Р2 = 3Р1 - 3Р_пари + Р_пари = 3Р1 - 2Р_пари     (4). 

Із (4) знаходимо Р_пари :       Р_пари = (3Р1 - Р2)/2.

     Р_пари = (3·76 см рт.ст. – 222 см рт.ст.)/2 = (228 см рт.ст. – 222 см рт.ст.)/2 =      = 6 см.рт.ст./2 = 3 см рт.ст. = 30 мм рт.ст.

    З таблиці знаходимо температуру при якій тиск насиченої пари рівний  30 мм рт.ст. :   t = 29ºС.

Відповідь.  Тиск пари 30 мм рт.ст. а температура 29ºС.

     Задача13

     У посудині міститься насичене водяною парою повітря при температурі 30ºС і тиску 800 мм рт.ст. Визначити тиск сухого повітря за даних умов, а також тиск повітря з парою, якщо посудину охолодити до 20ºС. t₁ = 30ºC                        Знайдемо в таблиці значення тиску насиченої пари:

P1 = 800 мм рт.ст.         Р_{нас.пари(30ºС)} = 31,8 мм рт.ст. t₂ = 20ºC                         Р_{нас.пари(20ºС)} = 17,5 мм рт.ст.

Р1сух.пов. - ?  Р2 - ?          Р1сух.пов. = Р1 - Рнас.пари(30ºС) = 800 мм рт.ст. – 31,8 мм рт.ст. = 768,2 мм рт.ст.

Для знаходження тиску сухого повітря після охолодження скористаємося законом Шарля:   Р1сух.пов./Т1 = Р2сух.пов./Т2.  

Звідси знаходимо:  Р2сух.пов. = (Т2·Р1сух.пов.)/Т1 . Т₁ = 273 + 30 = 303 К;

Т₂ = 273 + 20 = 293 К.

Р_{2сух.пов.} = (293·768,2 мм рт.ст.)/303 = 225082,6 мм рт.ст./303 = 742,8 мм рт.ст.

Тоді: Р2 = Р2сух.пов. + Рнас.пари(20ºС).

Р₂ = 742,8 мм рт.ст. + 17,5 мм рт.ст. ≈ 760 мм рт.ст.

   Відповідь. Початковий тиск сухого повітря 768,2 мм рт.ст. Тиск в посудині після охолодження 760 мм рт.ст.

 

 

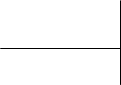
Таблиця 1. Тиск і густина насиченої пари при різних температурах.

 

В таблиці температура tº подана в (ºС) градусах Цельсія); тиск р в міліметрах ртутного стовпчика (мм рт.ст.); m маса 1м³ пари, виражена в грамах, тобто густина насиченої пари (ρ) в г/м³. При температурах нижчих 0ºС дається значення тиску насиченої пари і густини над льодом.

 

 

 

 

 

 

 

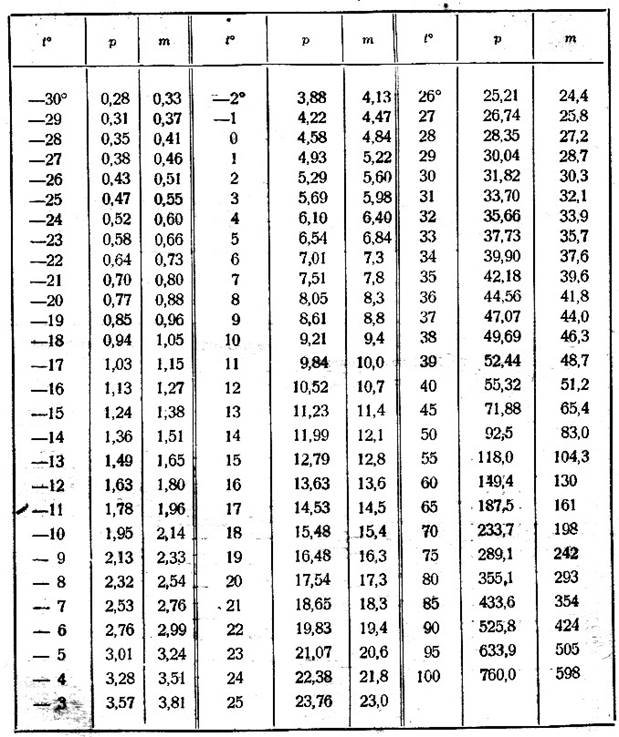
Таблиця 2. Тиск насиченої пари води при температурах вищих температури кипіння.

 

 

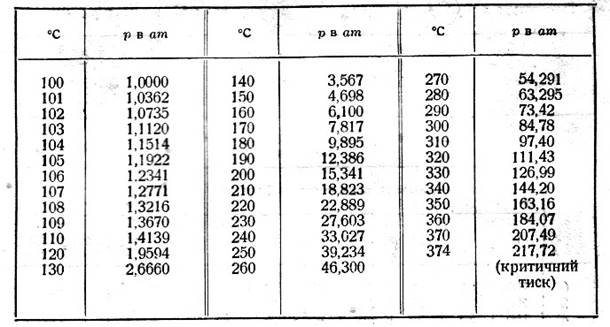
Таблиця 3. Тиск водяної пари над льодом.

 

 

 

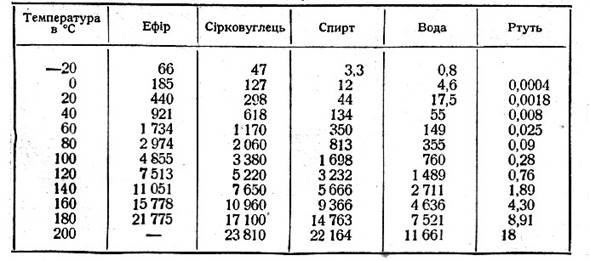
Таблиця 4. Тиск насиченої пари різних рідин при різних температурах

(у мм рт.ст.)

 

 

 

 

 

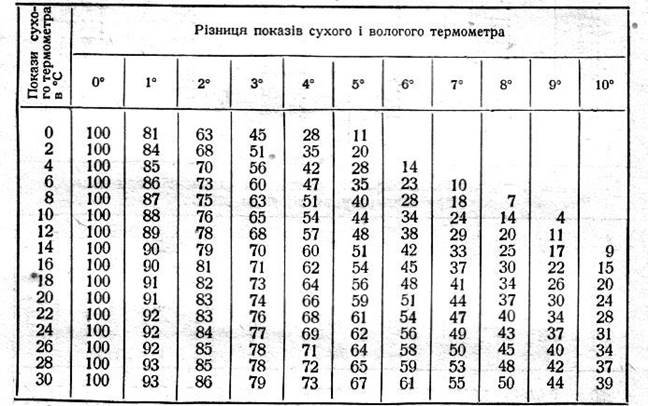
Таблиця 5. Психрометрична таблиця відносної вологості повітря.

 

Приклад користування таблицею. Нехай сухий термометр показує 22ºС, вологий 16ºС, отже різниця їх показів 6ºС. Тоді відносну вологість (у процентах) знайдемо на перетині рядка, на початку якого стоїть 22ºС, і стовпчика в заголовку якого стоїть 6ºС, у даному випадку відносна вологість дорівнює 54%.

 

 

 

Література.

1.     Гончаренко С.У. Фізика. 10 клас. Київ. “Освіта”. 1996.

2.     Дєдков М.Ф. Письмові контрольні роботи з фізики у 8-10 класах. “Радянська школа”. Київ. 1973.

3.     Кікоїн І.К. Молекулярна фізика. “Радянська школа”. Київ. 1968.

4.     Римкевич А.П. Збірник задач з фізики. “Радянська школа”. Київ. 1989.