«Узагальнення та систематизація знань та вмінь з теми: Заняття з математики. Тема:«Елементи комбінаторики, теорії ймовірностей та математичної статистики»

План – конспект  заняття з математики

Спеціальність: 121 « Розробка  програмного забезпечення»

Дисципліна: математика

Тема  заняття:  «Узагальнення та систематизація знань та вмінь з теми: «Елементи комбінаторики, теорії ймовірностей та математичної статистики»

Мета заняття:

навчальна:  повторити, систематизувати та узагальнити знання основних видів сполук та правил і формул комбінаторики, основних понять теорії ймовірностей та елементів математичної статистики; усвідомити значення математичної статистики, статистичний аналіз даних, наочне зображення статистичного розподілу; усвідомити значення математичної статистики, її місце у житті людей, систематизувати вміння застосовувати набуті знання до розв’язування задач, передбачених програмою ЗНО з математики;

розвиваюча: розвивати логічне мислення, пам'ять, культуру математичного мовлення, вміння спілкуватись, аналізувати ситуацію, оцінювати свої дії та дії своїх одногрупників; сприяти розвитку комунікативної, інформаційної, соціальної полікультурної компетентності. А також самоосвіти й саморозвитку, продуктивної творчої діяльності;

виховна: виховувати уважність, кмітливість, працьовитість, , вміння долати труднощі; самостійність та комунікабельність, самокритичність й загальнокультурні навички.

Тип заняття: узагальнення та систематизація знань, умінь і навичок.

Форма проведення: заняття- квест.

Наочність та обладнання: мультимедійний комплекс, авторська презентація,  інформаційні листівки, буклети, картки досягнень студентів, індивідуальні завдання.

План  заняття

Спеціальність: 121 « Розробка  програмного забезпечення» ,

 Дисципліна: математика

 Викладач: Опята Л.І.

 Тема  заняття.  Узагальнення та систематизація знань та вмінь з теми: «Елементи комбінаторики, теорії ймовірностей та математичної статистики»

План заняття

І  Організаційно-психологічна частина

ІІ  Формулювання теми, мети, завдань заняття. Мотивація навчальної діяльності

ІІІ Актуалізація опорних знань.

1. Перевірка домашнього завдання.
2. Фронтальне опитування.
3. Усний рахунок.

IV Цікаві повідомлення. Метод проектів.

V Самостійна робота.

VI Колективне розв’язування вправ.

VII Підведення підсумків заняття. Рефлексія.

VIII Домашнє завдання.

Бажаю УСПІХУ!

Як досягти успіху в житті?

Якщо бажаєте досягти в житті успіху,

 зробіть наполегливість своїм  кращим  другом,

досвід мудрим радником,

обережність – старшим братом,

 а надію – ангелом-охоронцем

Хід заняття

І. Організаційно-психологічна частина

Вітання з студентами.

Викладач: Народна мудрість говорить «Знання збираються по краплині, як вода в долині».   І далі: «Єдиний шлях, що веде до знань – діяльність», - писав Бернард Шоу. Знання – це сила, знання – це успіх.

Як досягти успіху? Це питання постає перед нами практично щодня. І як доречно буде вам винести з коледжу не тільки багаж теоретичних знань та практичних умінь, а й деякі рецепти досягнення успіху.  Тому я пропоную вам не тільки попрацювати з математичним матеріалом, а й  відповісти на запитання: що саме допомогло нам досягти успіху?

Я переконана, що успіх буде, і від щирого серця вам його бажаю.

Побажайте й ви один одному успіху.

 Сьогоднішнє заняття ми проведемо у формі квесту.  Кожен з вас має картку досягнень (додаток Б) на занятті, працюватимемо за відомими вам критеріями оцінювання.

ІІ. Формулювання теми, мети, завдань заняття. Мотивація навчальної діяльності

Викладач:  (формулює тему заняття)

Узагальнення і систематизація знань та вмінь з теми: «Елементи комбінаторики, теорії ймовірностей та математичної статистики»

Досягти можна успіху тільки тоді, коли є певна мета. Сформулюємо мету, завдання заняття.

 Систематизувати вміння застосовувати набуті знання до розв’язування задач, передбачених програмою ЗНО з математики.

Зробіть записи у зошитах: дата, тема.

IІІ. Актуалізація опорних знань.

  1Перевірка домашнього завдання. Станція «Домашня» (див. презентацію)

    2 Фронтальне опитування. Станція  «Теоретична.» Метод «Мікрофон»

Для того, щоб перейти до розв'язування задач, спочатку пригадаємо основні твердження та теореми, які нам знадобляться сьогодні на занятті.

1. Комбінаторні формули:

-перестановка (впорядкована множина з n елементів)                             

-розміщення (впорядкована множина з n елементів по m)                      

-комбінація (будь-яка невпорядкована множина з n елементів по m)                     

2. Схема розв’язування комбінаторних задач

Вибір правила:

-правило суми:       А    або    В         (m+n) способами;

-правило добутку:  А     і    В             mn cпособами. 

Вибір формули:

1.Чи всі елементи входять до сполуки?

                 ні                           так       

2.Чи враховується порядок розміщення елементів?

         ні                                   так         

         3 Дайте означення ймовірності випадкової події.

Класичне означення  ймовірності :Р(А)= ,

m-число сприятливих елементарних подій;  n- число всіх рівноможливих подій.

0<Р(А)<1-випадкова подія;

Р(А)=0- неможлива подія;

Р(А)=1-вірогідна подія.

4  У чому полягає теорема про суму ймовірностей подій?

5 Які події називаються протилежними? Чому дорівнює сума ймовірностей протилежних подій?

6  У чому полягає теорема про добуток ймовір­ностей подій?

7  Якою теоремою користуються для визначенні ймовірності появи хоча б  однієї випадкової події?

 8 Математична статистика:

- Що таке частотна таблиця;

-ранжирування ряду; розмах; мода; медіана; середнє значення;

-полігон частот; гістограма (графічне подання інформації).

3 Усний рахунок.

1. Скількома способами можна розподілити:

а) три однакові туристичні путівки між 10 робітниками;

б) три різні туристичні путівки між 10 робітниками;

в) 10 однакових путівок між 10 робітниками;

г) 10 різних путівок між 10 робітниками?

        2.   У шухляді лежать 8 червоних, 2 синіх і 20 зелених олівців. Ви навмання виймаєте олівець. Яка ймовірність того, що це

           а) червоний олівець; б) жовтий олівець; в) не зелений олівець.

          Яку найменшу кількість олівців треба вийняти, щоб із ймовірністю рівною 1, серед них був зелений олівець?

          3. Тестові завдання містять 5 варіантів відповідей, із яких лише одна правильна. Студент не знає відповіді на 2 тестових завдання і відповідає наугад. Яка ймовірність, що студент:

            а) дасть правильну відповідь на обидва завдання;

            б) дасть неправильну відповідь на обидва завдання;

            в) дасть правильну відповідь на одне завдання?

  4. Студенти однієї з груп під час сесії повинні скласти п’ять іспитів. Заступнику декана потрібно призначити складання цих іспитів на п’ять визначених дат. Скільки всього існує різних варіантів розкладу іспитів для цієї групи?

  5 До складу української Прем’єр-ліги з футболу входять 16 команд. Упродовж сезону кожні 2 команди грають між собою два матчі. Скільки усього матчів буде зіграно за сезон?

  6 Кодовий замок на дверях має десять кнопок, на яких нанесено десять різних цифр (див. рисунок). Щоб відчинити двері, потрібно одночасно натиснути дві кнопки, цифри на яких складають код замка. Скільки всього існує різних варіантів коду замка? Уважайте, що коди, утворені перестановкою цифр (наприклад, 1-2 і 2-1), є однаковими.

  7  Пасічник зберігає мед в однакових закритих бідонах. Їх у нього дванадцять: у трьох бідонах міститься квітковий мед, у чотирьох – мед із липи, у п’яти – мед із гречки. Знайдіть ймовірність того, що перший навмання відкритий бідон буде містити квітковий мед.

IV Цікаві повідомлення. Станція  «Практична.»  Метод проектів.

Заздалегідь група розбивається на 3 команди. Кожна команда отримує завдання підібрати і презентувати задачу практичного змісту з використанням теорії ймовірності.

Викладач.  Перейдемо до результатів роботи за завданнями проекту. Студенти, що працюватимуть біля дошки, повинні пам’ятати «Знання збільшуються, а вміння вдосконалюються, коли ними ділишся» - про це говорить народна мудрість.

V. Самостійна робота. СТАНЦІЯ «АЗАРТНА»

 Систематизація знань і умінь під час виконання самостійної роботи.

Викладач: Давня китайська мудрість говорить: « покажи мені – і я запам’ятаю, дай мені діяти самому – і я навчусь…»

Перед вами картки із завданнями і невеликі картки для перевірки відповідей. До кожного завдання дана одна картка з відповіддю. Розмістить їх під час розв’язування за порядком номерів завдань.

Кажуть: Успіх приходить до того, хто  мислить  категоріями Успіху, Тож бажаю Вам успіхів у виконані  тесту.

Самостійна робота

Щоб перевірити результати самостійної роботи, розглянемо картки з відповідями і, не міняючи їх місцями, перевернемо. Якщо ви правильно все зробили, то дістали слово «успіх» (додаток В). Підніміть руку ті, хто одержав це слово. Молодці! Ви досягли успіху. Іншим раджу не засмучуватися – ви теж досягли певного успіху. Український філософ і письменник Г. Сковорода писав: «Найкраща помилка та, яку допускають у навчанні».

 Студенти проводять самооцінювання самостійної роботи, виставляють бали у картку досягнень.

VII Колективне розв’язування вправ. Станція « Успішна».

Викладач. Студенти, що працюватимуть біля дошки, повинні пам’ятати «Знання збільшуються, а вміння вдосконалюються, коли ними ділишся» - про це говорить народна мудрість.

Задача 1. Наприкінці останнього тижня навчання зібрали відомості про кількість пропущених уроків математики учнями випускного класу за цей місяць. Отримали такі дані: 2, 5, 0, 1, 6, 3, 0, 1, 5, 4, 0, З, З, 2, 1, 4, 0, 0, 2, З, 6, 0, 3, 0. Побудувати полігон, знайти моду, медіану.

Визначити, яку кількість уроків пропустив у середньому кожен учень.

= –кількість уроків, які пропустив у середньому кожен учень.

Задача 2 (ЗНО) .  У місті Х запроваджено 7-цифрову нумерацію телефонів. Пан Карайко має намір зателефонувати до пані Лариси, що проживає в іншому районі міста. Пан Карайко пам’ятає, що всі цифри її телефонного номера різні, але забув три останні з них. Яка ймовірність того, що перша спроба пана Карайка набрати правильний номер буде вдалою?

Задача 3 . Три стрільці, для яких імовірності влучення в мішень дорівнюють 0,8;  0,75;  0,7 роблять по одному пострілу. Знайдіть імовірність того, що

а) тільки один із стрільців влучить у мішень;

б) жоден із стрільців не влучить;

в) перший влучить обов’язково.

г) принаймні один із  стрільців  влучить у мішень.

Задача 4 (ЗНО) .

Задача 5 (ЗНО) .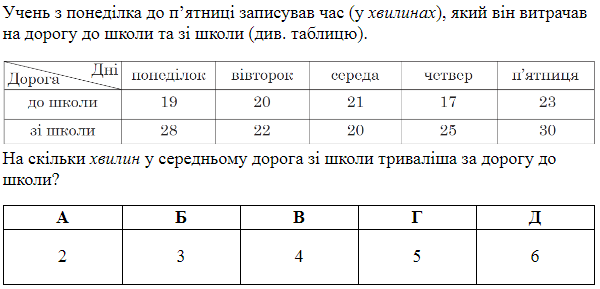

Задача 6(ЗНО) .

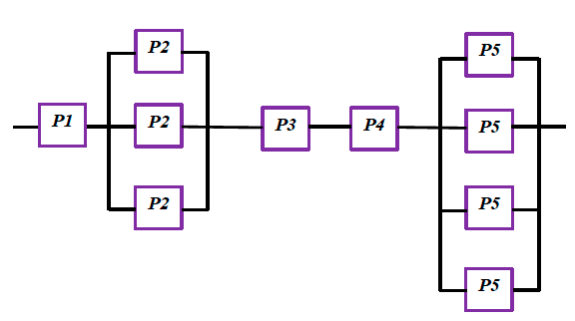
Задача 7  . В комп'ютерній мережі дубльовані не всі, а тільки деякі(більш важливі) вузли. Визначити надійність роботи мережі, якщо різноманітні елементи мережі працюють  незалежно один від одного, з імовірностями  безвідмовної  роботи вузлів такі:Р₁ =0,8; Р₂ =0,7; Р₃ =0,8; Р₄ =0,8; Р₅ =0,9

Підсумок заняття, рефлексія. СОВА

Айсберг успіху. Бажаю успіху!

Х. Домашнє завдання  Викладач: У житті та й у навчанні часто для досягнення успіху треба вміти працювати без допомоги, повністю самостійно. Це ви будете робити під час виконання домашнього завдання.

Підручник: Мерзляк А, Номіровський Д,  Полонський В, Якір М. «Математика 11», рівень стандарту,  Харків, «Гімназія», 2019

Перший рівень: ст.177, №24.189, №24.194;№24.205, №24.207 ,

 на повторення №25.1- 25.3

Другий рівень: ст.177 №24.192,№24.198, №24.203,№24.206,

 на повторення№25.1- 25.3 

Третій рівень: ст.177 №24.192,  №24.198,  №24.203,  №24.204,  №24.206,

на повторення №25.1- 25.3