Застосування похідної до розв'язування задач

ТЕМА УРОКУ:

Застосування похідної до розв'язування задач

Мета уроку: Мотивація застосування похідної функції до розв'язання задач Формувати знання, уміння учнів знаходити найбільше і найменше значення функцій при розв'язуванні задач прикладного характеру.

Виховувати у учнів звичку доводити розпочате до кінця, наполегливість у досягненні поставленої мети і прагнення і здатність до подолання труднощів.

Обладнання: дидактичні картки, схема дослідження функції, картки емоційного настрою, листки самоконтролю.

Очікувані результати:

Після уроку учні зможуть досліджувати функцію, знаходити найбільше і найменше значення функції. Складати математичну модель задачі, працювати з моделлю, відповідати на запитання задачі, знаходити оптимальне рішення.

Епіграф до уроку:

Найдосконаліший розум ржавіє без діла.

Девіз уроку:

Щоб вирішити важливі справи,

Не знати в житті невдач,

Похідну треба вміти застосувати

До цікавих практичних задач.

ХІД УРОКУ.

І. Організаційний момент

Ознайомити учнів з темою уроку.

Разом з учнями сформувати мету уроку, ознайомити з епіграфом, як він має бути пов'язаний з уроком, з кожним з присутніх на уроці.

Мотивація уроку:

Багато типових ситуацій з нашого побуту може обернутися необхідністю розв'язання деякої задачі, причому оптимально, тобто розпорядитися коштами, мінімальні витрати при максимальній користі; для цього потрібно встановити залежність між величинами.

II. Актуалізація опорних знань

Згадуємо з учнями схему дослідження функції (кожний учень отримує аркуш

зі схемою).

Схема дослідження функції

1.     Область визначення функції
2.     Область значень функції
3.     Парність
4.     Періодичність
5.     Точки перетину графіка функції з віссю ОХ та віссю ОУ
6.     Знайти похідну функції
7.     Знайти критичні точки
8.     Знайти проміжки знакопостійності похідної
9.     Заповнити таблицю
10. Побудувати графік функції

Бажаю успіху!

______________________________________________________________________

Три учня відповідають біля дошки

1.  учень - №603.
2.  учень - дидактична картка.
3.  учень - дидактична картка.

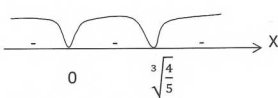
Перша картка: Дослідити функцію та побудувати її графік У = .

Друга картка: Дослідити функцію та побудувати її графік У =

_______________________________________________________________________

Розв'язання № 603

f (х)=х+х²; D(f)=R

f '(х)=1+2х

1+2х=0

Х=-

                                                    -

f'(-1)=1-2 = -1<0

f'(0)=1+0 = 1 >0 1

Відповідь: число - в сумі з його квадратом має найменше значення

______________________________________________________________________

Розв'язання завдань з дидактичних карток

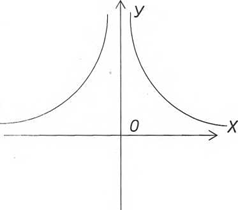
Y=

D(у) = R, крім 0 

Y’=-

Критична точка: 0

Парна, неперіодична

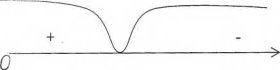Точок перетину з віссю ОХ, OY немає

f’(-1)=2>0

f’(1)=-2<0

______________________________________________________________________

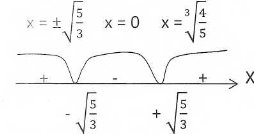
Розв'язання завдань з дидактичних карток

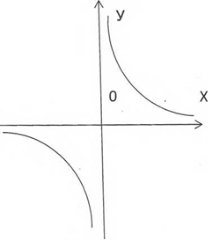
Y=

D(у) = R, крім 0 

Y’=-

Критична точка: 0

Парна, неперіодична

Точок перетину з віссю ОХ, OY немає

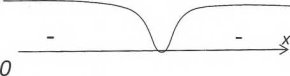
f’(-1)=-6<0

f’(1)=-6<0

В цей час з класом проводиться  математичний диктант на два варіанта (7-8 хвилин). Рисунок з графіком функції вішаю на дошку.

1.                    Чи є функція, графік якої зображено на рисунку, неперервною? 1 бал
2.                    Скільки критичних точок має ця функція?                           1 бал
3.                    Вказати знак похідної в точці х₁                                                                                 1бал
4.                    Вказати знак похідної в точці х₂                                                                                 1 бал
5.                    Вказати знак похідної в точці х₃                                                   1 бал
6.                    Скільки точок максимуму?                                                               0,5 бала
7.                    Скільки точок мінімуму ?                                                               0,5 бала
8.                    Назвіть точки максимуму та мінімуму.                                            1 бал
9.                    Назвіть значення функції в точках її екстремуму.                           1 бал
10.                Яка функція може мати похідну

у’ = Зх²-х + 7                                             у' = 5х⁴ + х³-2 ?                              2 бали

11.Знайти похідну функції

f (х) = х cos х                                             f (х) = х / cos х                               2 бали

Зібрати на перевірку.

Самоперевірка (два учні озвучують). Плакат з відповідями вішаю на дошку. Перевірка роботи учнів біля дошки (одна хвилина на коментарі).

______________________________________________________________________

Хвилина відпочинку

1.                    Учні презентують похідну віршем.

В класі разом ми сьогодні

Презентацію проведем

 Відпочинем, посміхнемось

І вивчати похідну почнем.

Що це за таке завдання?

Графік, похідна, рівняння...

Сам ти з цим не розберешся

 І до вчителя звернешся.

Намалює і розкаже,

Вчитель все тобі покаже,

Розповість тобі чимало,

Щоб тобі цікаво стало!

Навіщо людям похідна,

Адже й без неї жити можна!

А відповідь не це проста

І знає це людина кожна.

Похідну тобі треба знати,

Щоб всі критичні точки розв'язати.

А жінка скаже: « Хочу ванну!»,

А плитка нині дорогенька,

Не дай-то Бог купити лишню

Ти скажеш: « Похідна, допоможи, рідненька!».

І гривню хочеш ти лишить у себе,

А жінка вимагає ванну з тебе.

Тоді похідна тобі скаже:

« Якби ти вчив мене як треба То не займав би грошей у сусіда,

Щоб плитку інших розмірів купити».

Отож бо, хлопче, треба було вчити,

А висновок таки зробити треба –

Щоб не займати грошей у сусіда,

Ти краще гарно вивчи похідну,

Бо потім вчити будеш тему вже нову!

2.                    Чи знаєте ви, що?

• Найсильніший м'яз людини - це язик.
• Звичайна людина, у середньому, посміхається 10 разів на день.
• Хто частіше посміхається, той довше живе.

____________________________________________________________________

ПІ. Розв'язування задач

Згадати схему знаходження найбільшого та найменшого значення функції ( кожний учень отримує листочок зі схемою).

Знаходження найбільшого та найменшого значень функції на проміжку.

1. Знайти похідну функції

2. Знайти критичні точки функції

3. Визначити, які з цих точок належать проміжку, які йому не належать

4. Знайти значення функції в критичних точках та на кінцях проміжку

5. Вибрати з отриманих значень найбільше та найменше

6. Записати відповідь

Досягайте в успіхах максимуму, а в невдачах - мінімуму!

____________________________________________________________________

№601 (а, б, на два варіанти)   (№ 600 додатковий )

а) f(х) = х³ - 5х + 2                                                  б) f(х) = 3 - 2х²+х⁵

f' (х) = 3х²- 5                                                               f ' (х) = - 4х + 5х⁴ = -х ( 4- 5х³)

                       Зх²- 5 = 0 - х ( 4 - 5х³) = О

f' (- 2) = 3*4 - 5 = 7 >0                                                     f’(-1) = 4 - 5 = - 1< О

f' (0) = - 5 < О                                                                   f’ (0,1) = - 0,4 – 5*0,0001 < О

 f’ ( 2) = 3*4-5 = 7 >0                                                       f’(1)=-4-5<0

Відповідь: функція має максимум і мінімум.               Відповідь: функція не має точок

                                                                                            максимуму та  мінімуму

_________________________________________________________________________

Задача.

За периметром вікна 6 м зробити вікно найбільшої площі, щоб освітленість була

найкраща.

Модель: вікно - прямокутник

 S= аb

Р = 2(а + b) = 6 м.

 а = х, b = 3 - х

S (х) = х ( 3 - х), 0 < х < 3

 Розв'язання

S’(х) = 3 - 2х

 3- 2х = 0

х =1,5

1/5

                   1,5

S ' (0) = 3 > 0

S'(2) = 3-4 = -1<0

Отже, х = 1,5 - точка максимуму функції.

Знайдемо значення функції в цій точці: S( 1,5 ) = 2,25.

Відповідь: максимальна площа вікна  S= 2,25 м² .

Якщо залишається час, то розв'язуємо додатково N 605.

_________________________________________________________________________

4. Підсумки уроку

Чим ми сьогодні займались на уроці?

Як це можна застосувати у житті?

Що сподобалось на уроці?

Що з розглянутого матеріалу залишилось незрозумілим?

Рефлексія: учні заповнюють листки самоконтролю ( що дає змогу вчителю прослідкувати за емоційним станом учнів).

_______________________________________________________________________

Лист самоконтролю

1 Мої знання відповідають наступному смайлику:

- повністю володію матеріалом

 - потрібна допомога

- не володію матеріалом

2. Чи досяг я мети на уроці? ( так або ні)

3. Я працював на уроці на _____________________%

    Заслуговую на________________ 

4.Чи потрібна допомога під час виконання домашнього завдання? ( так чи ні).

________________________________________________________________________

5.   Домашнє завдання

Параграф З0 - 32 повторити, № 606 письмово, навести приклади задач, що використовують похідну.

Кожному учню роздаю листочок з індивідуальним домашнім завданням.

_________________________________________________________________________

Індивідуальне домашнє завдання з математики: виконати програму мінімум - стати студентом ВУЗу; знайти своє місце в житті; бути людиною! Нехай Ваші успіхи утворять геометричну прогресію, а невдачі будуть настільки мізерними, що ними можна знехтувати.                             

З повагою В.Т. Сирова. Щасти Вам!

________________________________________________________________________

Використана література : Г . П . Бевз . Алгебра і початки аналізу .10-11 клас .Київ .

2006 рік.