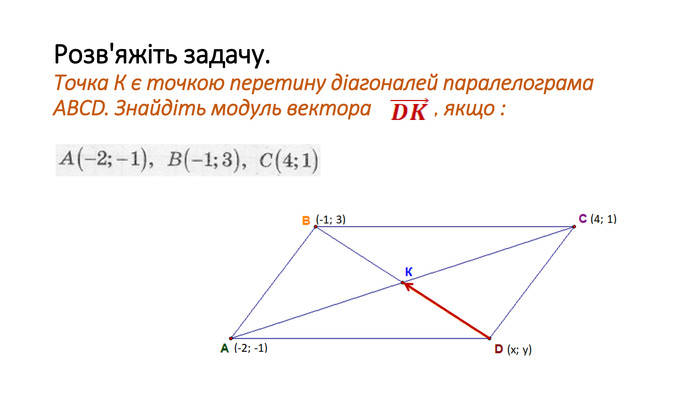
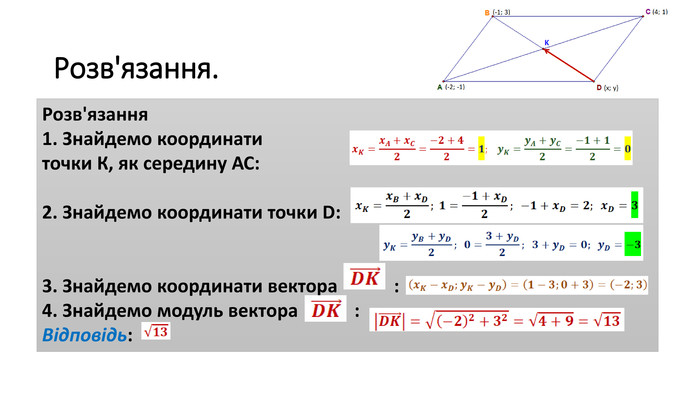
Вектор. Модуль і напрям вектора. Рівість векторів. Координати вектора
Про матеріал
Презентація може бути використана при підготовці до контрольної роботи або для класної роботи при розв'язуванні задач з теми при дистанційному навчанні
Перегляд файлу
Зміст слайдів


Безкоштовний сертифікат
про публікацію авторської розробки
про публікацію авторської розробки
Щоб отримати, додайте розробку
Додати розробку