«ВЕКТОРИ НА ПЛОЩИНІ» НАВЧАЛЬНИЙ ПОСІБНИК ДЛЯ 9 КЛАСУ
 ЛІЦЕЙ №4
ЛІЦЕЙ №4
МІСТА НОВОГРАДА-ВОЛИНСЬКОГО
ЖИТОМИРСЬКОЇ ОБЛАСТІ
«ВЕКТОРИ НА ПЛОЩИНІ»
НАВЧАЛЬНИЙ ПОСІБНИК
ДЛЯ 9 КЛАСУ
НОВОГРАД-ВОЛИНСЬКИЙ – 2019
ЗМІСТ
ВСТУП……………………………………………………………………………..4
РОЗДІЛ 1. ДЕРЖАВНІ ВИМОГИ ДО РІВНЯ ЗАГАЛЬНООСВІТНЬОЇ ПІДГОТОВКИ УЧНІВ З ТЕМИ «ВЕКТОРИ НА ПЛОЩИНІ………………....5
РОЗДІЛ 2. ТЕОРЕТИЧНИЙ АСПЕКТ ТЕМИ «ВЕКТОРИ НА ПЛОЩИНІ»
2.1. Поняття вектора……………………………………………..……….…6
2.2. Дії над векторами…………………………………………………...…10
2.2.1. Дії над векторами, заданими геометрично…………………...10
2.2.2. Дії над векторамив координатному поданні…………………14
2.3. Скалярний добуток векторів………………………………………….14
2.4. Розкладання вектора за двома неколінеарними векторами………..16
РОЗДІЛ 3. ПРАКТИЧНИЙ АСПЕКТ ТЕМИ «ВЕКТОРИ НА ПЛОЩИНІ»
3.1. Практичні завдання…………………………………………………....18
3.2. Вправи………………………………………………………………….20
3.3. Розв’язування геометричних задач векторним способом………….22
3.4. Застосування векторів до розв’язування задач………………...……22
3.5. Завдання для перевірки знань………………………………………...25
СПИСОК ВИКОРИСТАНИХ ДЖЕРЕЛ……………………………………….28
ДОДАТКИ………………………………………………………………………..29
Додаток 1……………………………………………………………………29
Додаток 2……………………………………………………………………30
Додаток 3……………………………………………………………………34
ВСТУП
Серед усіх наук, що відкривають людству
шлях до пізнання законів природи,
наймогутніша, найвеличніша наука – математика
С. Ковалевська
Математика – це фундаментальна наука, методи якої активно застосовуються в багатьох природничих дисциплінах, таких як фізика, хімія і навіть біологія. Сама по собі ця область знань оперує абстрактними відношеннями і взаємозв'язками, тобто такими сутностями, які самі по собі не є чимось природним.
Але, варто лише математиці вступити в область будь – якої науки про світ, вона відразу втілюється в опис, моделювання та передбачення цілком конкретних і реальних природних процесів. Тут вона знаходить сутність, виходячи з під покриву ідеалізованих та відірваних від життя формул і підрахунків.
Математика – інструмент світу. Вона являє точну науку, яка не терпить хаосу в тлумаченнях. Це втілення порядку і жорсткої логіки. Без неї розвиток технологій і визнання природи були б немислимими речами. Тепер математика потрібна всім. Збільшується не тільки кількість наук, які вже не можуть обходитись без математики, а й обсяг математичних знань, що використовується цими науками. Ось чому так важливо, щоб наша молодь мала ґрунтовну математичну підготовку.
Однією з найважливіших проблем сьогодні в нашій країні є проблема освіти, сутність якої полягає в тому, що в учнів знизився інтерес до вивчення, як усіх предметів, так і математики зокрема. Тому мета навчального посібника полягає у підвищенні інтересу до вивчення математики.
Для досягнення високого рівня геометричної підготовки учнів необхідно забезпечити можливість придбання ними глибоких фундаментальних знань, розвитку уяви, прагнення до самостійного вивчення нового матеріалу. Вирішенню цієї проблеми сприяє розв’язування геометричних задач, що є ефективним засобом управління пізнавальною діяльністю і формуванням логічного, критичного мислення учнів. В посібнику в достатній мірі наведені зразки розв’язування задач різної складності, які стимулюють учнів до здобуття нових знань, збагачують їх теоретичними і практичними знаннями. В посібнику матеріал, що вивчається викладено згідно з цілями навчання, визначеними програмою і державними вимогами до загальноосвітньої підготовки учнів. Він складається з теоретичного і практичного компонентів. Практичний компонент – це важливий засіб розвитку творчих здібностей школярів, формування рис характеру, поглядів і переконань, інтересу до знань, підготовки учнів до життя.
Учитися треба для того щоб стати компетентним. Математика дає змогу людині відчути силу розуму, свою велич.
РОЗДІЛ 1
ДЕРЖАВНІ ВИМОГИ ДО РІВНЯ ЗАГАЛЬНООСВІТНЬОЇ ПІДГОТОВКИ УЧНІВ З ТЕМИ «ВЕКТОРИ НА ПЛОЩИНІ»
Учень/учениця:
Наводитьприклади: рівних, протилежних, колінеарних векторів;
пояснює:
що таке: вектор; модуль і напрям вектора; одиничний вектор; нуль-вектор; колінеарні вектори; протилежні вектори; координати вектора; сума і різниця векторів; добуток вектора на число;
як задати вектор;
як відкласти вектор від заданої точки;
за якими правилами знаходять: суму векторів; добуток вектора на число;
формулює:
означення: рівних векторів; скалярного добутку векторів;
властивості: дій над векторами;
зображує і знаходить на малюнках:
вектор; вектор, рівний або протилежний даному, колінеарний із даним,у т. ч. за його координатами; вектор, що дорівнює сумі (різниці) векторів, добутку вектора на число;
обчислює:
координати вектора, суми (різниці) векторів, добутку вектора на число;
довжину вектора, кут між двома векторами;
обґрунтовує: рівність, колінеарність, перпендикулярність векторів;
застосовує вивчені означення й властивості до розв’язування задач.
РОЗДІЛ 2
ТЕОРЕТИЧНИЙ АСПЕКТ ТЕМИ «ВЕКТОРИ НА ПЛОЩИНІ»
2.1. Поняття вектора. Координати вектора
Поняття вектора є одним із фундаментальних понять сучасної математики. Його можна визначати по-різному:
- як напрямлений відрізок;
- як упорядковану пару точок, що є кінцями напрямленого відрізка;
- як паралельне перенесення.
Вектор характеризується числовим значенням (модулем) і напрямом.
Вектор зображають напрямленим відрізком, тобто відрізком зі стрілкою, яка показує напрям вектора.
Для позначення векторів використовують малі латинські букви: а, b, c... або АВ… Перша з букв позначає початок, друга – кінець.
Риска або стрілка над назвою відрізка заміняє слово «вектор».
Щоб задати вектор, достатньо вказати його початок його кінець.
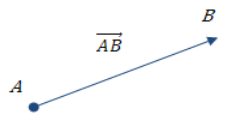
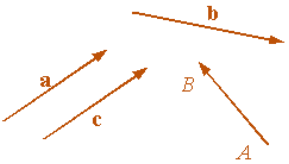
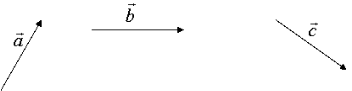
Рис. 1
Довжиною (модулем) вектора називають довжину відрізка, що зображує цей вектор.
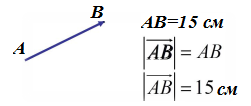
Рис. 2
Види векторів.
Два ненульових вектори називаються колінеарними, якщо вони паралельні одній прямій. Записують:![]() .
.
Рис. 3
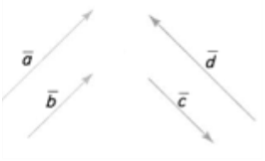
Колінеарні вектори ![]() , які мають однаковий напрям, називають однаковонапрямленими (співнапрямленими), якщо промені АВ і СD однаково напрямлені, і записують:
, які мають однаковий напрям, називають однаковонапрямленими (співнапрямленими), якщо промені АВ і СD однаково напрямлені, і записують:![]() .
.
Колінеарні вектори![]() , які мають протилежні напрями, називаютьпротилежнонапрямленими, якщопромені АВ і СD протилежно напрямлені,і записують:
, які мають протилежні напрями, називаютьпротилежнонапрямленими, якщопромені АВ і СD протилежно напрямлені,і записують:![]() .
.
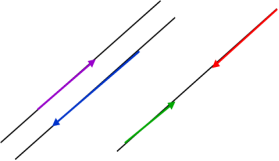
 Вектор, у якого початок і кінець співпадають, називають нуль-вектором (або нульовим вектором) і позначають:
Вектор, у якого початок і кінець співпадають, називають нуль-вектором (або нульовим вектором) і позначають: ![]() або
або ![]() .
.
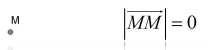
Рис. 4
Про напрям нуль-вектора не говорять.
Довжина нуль-вектора дорівнює нулю: l![]() l=0. Нульовий вектор вважають колінеарним будь-якому вектору.
l=0. Нульовий вектор вважають колінеарним будь-якому вектору.
Вектор, який має довжину 1, називається одиничним вектором.
Його позначають так:![]() . За означенням:
. За означенням:![]() = 1.
= 1.
Вектори називаються рівними, якщо вони співнапрямлені та мають рівні довжини (модулі).
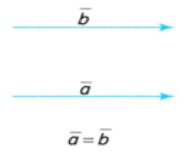
Рис.5
Отже, вектори є рівними, якщо виконано дві умови:
- вони однаково напрямлені;
- їхні модулі рівні, тобто
![]()
![]()
![]()
![]()
![]()
Від будь якої точки можна відкласти вектор, що дорівнює даному, до того ж лише один.
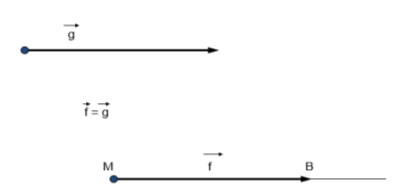
Рис.6
Якщо два вектори мають рівні довжини (модулі) і протилежно напрямлені, то їх називають протилежними векторами.
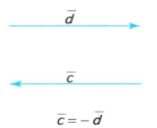
Рис.7
Координати вектора.
Впорядкована пара точок А і В визначає вектор ![]() .
.
Нехай точки А і В мають координати: А (х1; у1 ), В (х2; у2).
Числа![]() 1 = х2 – х1 і
1 = х2 – х1 і![]() 2 = у2– y1, називають координатами вектора
2 = у2– y1, називають координатами вектора![]() у даній системі координат.
у даній системі координат.
Коротко записують:
-
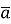 (
(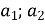 ) і читають: вектор а з координатами
) і читають: вектор а з координатами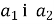 ;
;
-
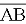 (
(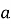 1;
1; 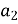 ) і читають: вектор
) і читають: вектор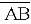 з координатами
з координатами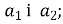
-
 (
(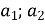 ) і читають: вектор з координатами
) і читають: вектор з координатами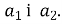
Координати нуль-вектора дорівнюють нулю: ![]() (0; 0).
(0; 0).
Протилежні вектори мають протилежні відповідні координати.
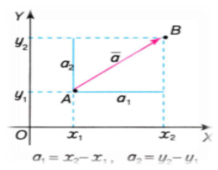
Рис. 8
Важливо: поняття координат вектора відрізняється від поняття координат точки на площині. Наприклад, точку М (2;1) можна позначити на координатній площині і ця точка буде єдиною. Знаючи координати точки, завжди можна знайти її положення на площині (у даному випадку І чверть). А ось векторів з координатими (2; 1) на площині можна зобразити безліч, головне, щоб різниці координат кінця і початку векторів були однакові, а вказати конкретно чверть, де знаходиться вектор з координатими (2; 1), – неможливо.
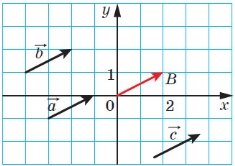
Рис. 9
![]()
![]() Формула для обчислення довжини (модуля) вектора
Формула для обчислення довжини (модуля) вектора![]() :
:
![]()
Властивість і ознака координат рівних векторів:
рівні вектори мають рівні координати, і навпаки: якщо у векторів відповідні координати рівні, то ці вектори рівні (рис. 10)
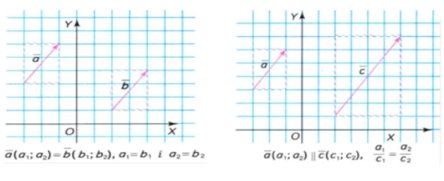
Рис. 10 Рис. 11
Властивість та ознака колінеарних векторів:
у колінеарних векторів відповідні координати пропорційні і, навпаки: якщо у двох векторів відповідні координати пропорційні, то ці вектори колінеарні (рис.11).
2.2. Дії над векторами
2.2.1. Дії над векторами, заданими геометрично
![]()
![]()
![]() Якщо тіло перемістилося з точки A в точку B, а потім із точки B у точку C, то сумарне переміщення з точки A в точку C природно подати у вигляді вектора АС, вважаючи цей вектор сумою векторів AB і BC, тобто
Якщо тіло перемістилося з точки A в точку B, а потім із точки B у точку C, то сумарне переміщення з точки A в точку C природно подати у вигляді вектора АС, вважаючи цей вектор сумою векторів AB і BC, тобто
![]()
![]()
![]() AB + BC = AC.
AB + BC = AC.
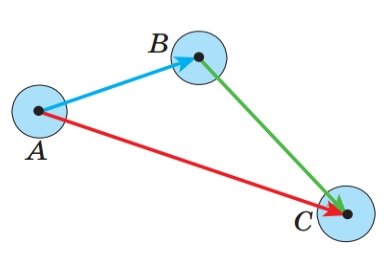
Рис.12
Правила додавання двох векторів:
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() правило трикутника: відкладемо від довільної точки A вектор AB, рівний вектору
правило трикутника: відкладемо від довільної точки A вектор AB, рівний вектору ![]() . Далі від точки B відкладемо вектор BC, рівний вектору b. Вектор AC називають сумою векторів a і b і записують: a + b = AC.
. Далі від точки B відкладемо вектор BC, рівний вектору b. Вектор AC називають сумою векторів a і b і записують: a + b = AC.
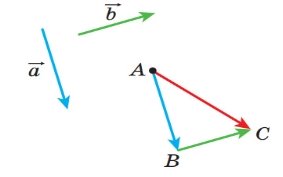
Рис.13
За правилом трикутника можна додавати й колінеарні вектори.
![]()
![]()
![]() Вектор AC дорівнює сумі колінеарних векторів а і b.
Вектор AC дорівнює сумі колінеарних векторів а і b.
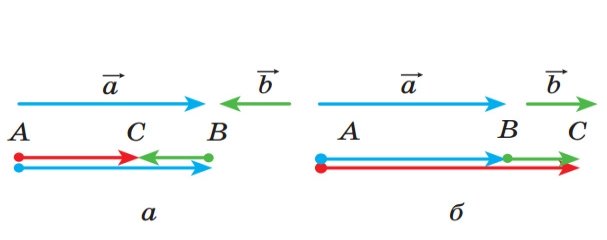
Рис.14
![]()
![]()
![]() Для будь-яких трьох точок A, B і C виконується рівність AB+ BC = AC, яка виражає правило трикутника для додавання векторів;
Для будь-яких трьох точок A, B і C виконується рівність AB+ BC = AC, яка виражає правило трикутника для додавання векторів;
правило паралелограма (для знаходження суми двох неколінеарних векторів, відкладених від однієї точки):
![]()
![]()
![]()
![]() відкладемо від довільної точки A вектор AB, рівний вектору
відкладемо від довільної точки A вектор AB, рівний вектору ![]() , і вектор AD, рівний вектору b. Побудуємо паралелограм ABCD. Тоді шукана сума
, і вектор AD, рівний вектору b. Побудуємо паралелограм ABCD. Тоді шукана сума
![]()
![]()
![]()
![]() + b дорівнює вектору AC.
+ b дорівнює вектору AC.
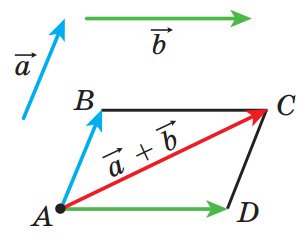
Рис.15
Правила додавання кількох векторів:
сума кількох векторів визначається за допомогою правила многокутника, яке є узагальненням правила трикутника. Якщо вектори відкладені так, що початок другого вектора збігається з кінцем першого, початок третього – із кінцем другого і т.д., то сума дорівнює вектору, початок якого збігається з початком першого, а кінець – із кінцем останнього вектора, тобто
![]()
![]()
![]()
![]()
![]()
![]() + b + c + d = e
+ b + c + d = e
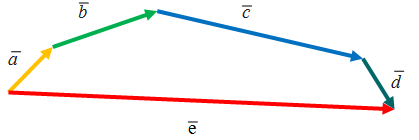
Рис. 16
Властивості додавання векторів:
![]()
![]()
![]() для будь-яких векторів
для будь-яких векторів ![]() , b і c виконуються рівності:
, b і c виконуються рівності:
![]()
![]() 1) a +0 = a – додавання нуль-вектора;
1) a +0 = a – додавання нуль-вектора;
![]()
![]()
![]()
![]() 2) a + b = b + a– переставна властивість;
2) a + b = b + a– переставна властивість;
![]()
![]()
![]()
![]()
![]()
![]() 3)(a+b)+c = a +(b + c)– сполучна властивість;
3)(a+b)+c = a +(b + c)– сполучна властивість;
![]()
![]() 4) a + ( - a ) = 0– додавання протилежних векторів.
4) a + ( - a ) = 0– додавання протилежних векторів.
Означення різниці векторів:
![]()
![]()
![]()
![]()
![]() різницею векторів a і b називають такий вектор c , сума якого з вектором b дорівнює вектору a.
різницею векторів a і b називають такий вектор c , сума якого з вектором b дорівнює вектору a.
![]()
![]()
![]() Пишуть: c= a - b.
Пишуть: c= a - b.
Побудова вектора, який є різницею двох векторів:
![]()
![]()
![]()
![]() від довільної точки O відкладемо вектори OA і OB, відповідно рівні векторам
від довільної точки O відкладемо вектори OA і OB, відповідно рівні векторам
![]()
![]()
![]() a і b. Тоді вектор BA дорівнює різниці a - b.
a і b. Тоді вектор BA дорівнює різниці a - b.
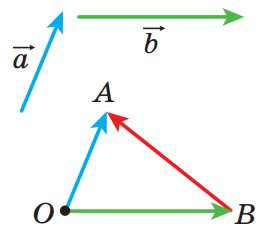
Рис. 17
Описаний алгоритм можна застосовувати й для знаходження різниці колінеарних векторів.
![]()
![]()
![]() Вектор BA дорівнює різниці колінеарних векторів a і b.
Вектор BA дорівнює різниці колінеарних векторів a і b.
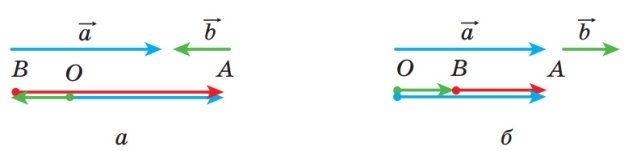
Рис. 18
Означення множення вектора на число:
![]()
![]() добутком ненульового вектора
добутком ненульового вектора ![]() і числа k, причому k≠0, називають такий вектор b, що:
і числа k, причому k≠0, називають такий вектор b, що:
![]()
![]() 1) |b| = |k| |
1) |b| = |k| |![]() |;
|;
![]()
![]()
![]()
![]() 2) якщо k > 0, то b ↑↑
2) якщо k > 0, то b ↑↑![]() ; якщо k < 0, то b↑↓
; якщо k < 0, то b↑↓![]() .
.
![]()
![]() Пишуть: b = k
Пишуть: b = k![]() .
.
![]()
![]()
![]() Якщо
Якщо ![]() 0 або k = 0, то вважають, що k
0 або k = 0, то вважають, що k![]() 0.
0.
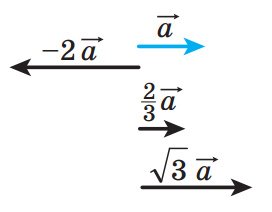
Рис.19
![]()
![]()
![]() Абсолютна величина вектора ka: |ka| = |k| |
Абсолютна величина вектора ka: |ka| = |k| |![]() |
|
![]()
![]() Умова колінеарності двох ненульових векторів a і b:
Умова колінеарності двох ненульових векторів a і b:
![]()
![]()
![]() якщо вектори
якщо вектори ![]() і b ‑колінеарні й
і b ‑колінеарні й ![]() ≠0, то існує таке число k, що
≠0, то існує таке число k, що
![]()
![]() b = k
b = k![]() .
.
Властивості множення вектора на число:
![]()
![]() для будь-яких чисел k, m і будь-яких векторів
для будь-яких чисел k, m і будь-яких векторів ![]() , b виконуються рівності:
, b виконуються рівності:
![]()
![]() 1) 1
1) 1![]() =
= ![]() ;
;
![]()
![]() 2) - 1
2) - 1![]() =
= ![]() ;
;
![]()
![]() 3) k 0 = 0
3) k 0 = 0 ![]() = 0;
= 0;
![]()
![]() 4) k
4) k![]() =
= ![]() k
k
![]()
![]() 5) (km)
5) (km)![]() = k (m
= k (m![]() ) — сполучна властивість;
) — сполучна властивість;
![]()
![]()
![]() 6) (k + m)
6) (k + m)![]() = k
= k![]() + m
+ m![]() — перша розподільна властивість;
— перша розподільна властивість;
![]()
![]()
![]()
![]() 7) k (
7) k (![]() + b) = k
+ b) = k![]() + kb — друга розподільна властивість.
+ kb — друга розподільна властивість.
2.2.2.Дії над векторами у координатному поданні
Позначення вектора, заданого своїми координатами:
![]() якщо вектор
якщо вектор![]() має координати
має координати ![]() то його позначають:
то його позначають:
![]()
![]()
![]() (
(![]() ) або (
) або (![]() ).
).
Сума двох векторів:
![]()
![]()
![]() сумою векторів
сумою векторів ![]() і b з координатами (
і b з координатами (![]() ) і (
) і (![]() ) називається вектор с з координатами
) називається вектор с з координатами ![]() тобто
тобто
![]()
![]()
![]()
![]() (
(![]() ) + b(
) + b(![]() ) = c
) = c![]() .
.
Різниця двох векторів:
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() різницею векторів
різницею векторів ![]() (
(![]() ) і b(
) і b(![]() ) називається такий вектор с(
) називається такий вектор с(![]() який у сумі з вектором b дає вектор
який у сумі з вектором b дає вектор ![]() : b + c =
: b + c = ![]() .
.
![]() Добуток вектора
Добуток вектора ![]() (
(![]() ) на число k:
) на число k:
![]()
![]()
![]()
![]() добутком вектора (
добутком вектора (![]() ) на число k називається вектор (k
) на число k називається вектор (k![]() ), тобто(
), тобто(![]() )k=(k
)k=(k![]() ).
).
Ознака колінеарності двох векторів :
у колінеарних векторів відповідні координати пропорційні і, навпаки: якщо у двох векторів відповідні координати пропорційні, то ці вектори колінеарні, тобто ![]()
2.3. Скалярний добуток векторів
![]()
![]() Кут між ненульовими векторами ОА і ОВ
Кут між ненульовими векторами ОА і ОВ
![]()
![]()
![]()
![]()
![]()
![]() Від довільної точки O відкладемо вектори OA і OB, відповідно рівні векторам
Від довільної точки O відкладемо вектори OA і OB, відповідно рівні векторам ![]() і b. Величину кута AOB називатимемо кутом між векторами
і b. Величину кута AOB називатимемо кутом між векторами ![]() і b.
і b.
![]()
![]()
![]()
![]() Кут між векторами a і b позначають так:∠(a,b).
Кут між векторами a і b позначають так:∠(a,b).
![]()
![]()
![]()
![]() Наприклад, на рисунку 1 ∠(a,b )= 120°, а на рисунку 2 ∠( m, n)= 180°.
Наприклад, на рисунку 1 ∠(a,b )= 120°, а на рисунку 2 ∠( m, n)= 180°.
![]()

а б
Рис.20
Важливо:
-



 якщо a ↑↑ b, то ∠( a,b )= 0°;
якщо a ↑↑ b, то ∠( a,b )= 0°;
-



 якщо, то a↑↓ b∠( a,b )= 180°;
якщо, то a↑↓ b∠( a,b )= 180°;
-

 якшо ∠( a,b )= 90°,то вектори називають перпендикулярними
якшо ∠( a,b )= 90°,то вектори називають перпендикулярними
![]()
![]()
![]()
![]() (пишуть a b).
(пишуть a b).
![]()
![]()
![]() Отже, для будь-яких векторів a і b має місце нерівність:
Отже, для будь-яких векторів a і b має місце нерівність:![]() ≤ ∠( a,b ) ≤
≤ ∠( a,b ) ≤ ![]()
Скалярний добуток векторів:
-

 скалярний добуток векторів a(
скалярний добуток векторів a(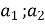 ) і b(
) і b(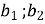 )
)
дорівнює сумі добутків відповідних координат цих векторів:
![]()
![]() ab =
ab = ![]() +
+ ![]() ;
;
-





 скалярним добутком двох ненульових векторів називають число, що дорівнює добутку їх довжин та косинуса кута між ними: ab = |a||b|cos∠(a,b)
скалярним добутком двох ненульових векторів називають число, що дорівнює добутку їх довжин та косинуса кута між ними: ab = |a||b|cos∠(a,b)
Властивості скалярного множення векторів:
![]()
![]()
![]()
![]()
![]() для будь-яких векторів a, b, c і будь-якого числа k виконуються рівності:
для будь-яких векторів a, b, c і будь-якого числа k виконуються рівності:
![]()
![]() 1) ab=ba — переставна властивість;
1) ab=ba — переставна властивість;
![]()
![]()
![]()
![]()
![]() 2)(ka)b=k(ab) — сполучна властивість (відносно скалярного множника);
2)(ka)b=k(ab) — сполучна властивість (відносно скалярного множника);
![]()
![]()
![]()
![]()
![]()
![]() 3) (a+b )c = ac + bc — розподільна властивість.
3) (a+b )c = ac + bc — розподільна властивість.
![]() Скалярний квадрат вектора а:
Скалярний квадрат вектора а:
![]()
![]()
![]()
![]() скалярним квадратом вектора а називають скалярний добуток а а і позначають:
скалярним квадратом вектора а називають скалярний добуток а а і позначають: ![]()
![]()
![]()
![]()
![]() Властивість і ознака перпендикулярних векторів:
Властивість і ознака перпендикулярних векторів:
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() якщо
якщо ![]() b, то
b, то ![]() b = 0 і, навпаки, якщо для ненульових векторів
b = 0 і, навпаки, якщо для ненульових векторів ![]() і b справедлива рівність
і b справедлива рівність ![]() b = 0, то
b = 0, то ![]() b
b
![]()
![]() Векторні рівності, що відповідають певним властивостям геометричних фігур:
Векторні рівності, що відповідають певним властивостям геометричних фігур:
- ОА=ОВ – точки А і В збігаються;
-

 АВ=kСD – прямі АВ і СD паралельні;
АВ=kСD – прямі АВ і СD паралельні;
-
 АВ=kАС – точки А,В,С лежать на одній прямій;
АВ=kАС – точки А,В,С лежать на одній прямій;
-


 АВ∙СD=0 – прямі АВ і СD перпендикулярні;
АВ∙СD=0 – прямі АВ і СD перпендикулярні;
-



 ОC=
ОC=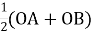 , де С– середина відрізка АВ, О – довільна точка площини. Цю рівність називають векторною рівністю середини відрізка;
, де С– середина відрізка АВ, О – довільна точка площини. Цю рівність називають векторною рівністю середини відрізка;
-



 ОМ=
ОМ=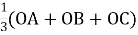 , де М – точка перетину медіан трикутника АВС, О – довільна точка;
, де М – точка перетину медіан трикутника АВС, О – довільна точка;
-


 ОМ=
ОМ=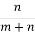 ОА+
ОА+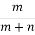 ОВ, де М– точка, що ділить відрізок АВ у відношенні АМ:МВ=m:n, О – довільна точка. Ця рівність виражає необхідну і достатню умову належності трьох точок А, В і С одній прямій:
ОВ, де М– точка, що ділить відрізок АВ у відношенні АМ:МВ=m:n, О – довільна точка. Ця рівність виражає необхідну і достатню умову належності трьох точок А, В і С одній прямій:
-




 якщо три точки лежать на одній прямій, а О – довільна точка площини, до того ж АМ : МВ= m : n, то ОМ=
якщо три точки лежать на одній прямій, а О – довільна точка площини, до того ж АМ : МВ= m : n, то ОМ=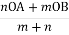 ;
;
-
 якщо справджується рівність ОМ=
якщо справджується рівність ОМ=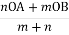 , то А, М, В точки лежать на одній прямій.
, то А, М, В точки лежать на одній прямій.
-


 MN=
MN=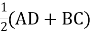 , де М і N – середини відрізків АВ і СD;
, де М і N – середини відрізків АВ і СD;
-
якщо відрізки А
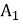 , В
, В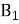 , С
, С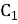 – медіани трикутника АВС, які перетинаються в точці М, то:
– медіани трикутника АВС, які перетинаються в точці М, то:
![]()
![]()
![]() 1) А
1) А![]() + В
+ В![]() + С
+ С![]() =0;
=0;
![]()
![]()
![]() 2) МА + МВ + МС =0;
2) МА + МВ + МС =0;
3) з відрізків А![]() , В
, В![]() і С
і С![]() векторно скласти трикутник.
векторно скласти трикутник.
2.4. Розкладання вектора за двома неколінеарними векторами
Координатні вектори (орти):
одиничні вектори, які мають напрями додатних координатних півосей прямокутної системи координат, називають координатними векторами (або ортами)
![]()
![]()
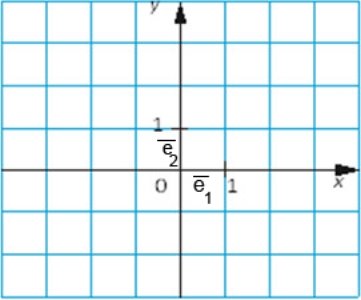
Рис.21
![]()
![]() Позначають
Позначають![]() (1;0) на осі Ох та
(1;0) на осі Ох та ![]() (0;1) на осі Оу.
(0;1) на осі Оу.
Розклад вектора за дома координатними векторами:
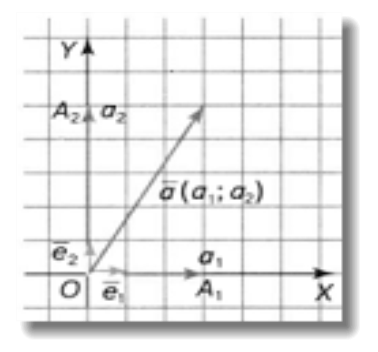
Рис.22
![]()
![]()
![]()
![]()
![]()
![]() Рівність
Рівність ![]() називають розкладом вектора
називають розкладом вектора![]() за двома координатними векторами
за двома координатними векторами ![]() , а числа
, а числа ![]() – коефіцієнтами розкладу.
– коефіцієнтами розкладу.
Коефіцієнти розкладу даного вектора за координатними векторами називають координатами вектора у певній системі координат.
![]()
![]()
![]()
![]() Наприклад, якщо АВ = 7
Наприклад, якщо АВ = 7![]() , то АВ(7;9).
, то АВ(7;9).
Важливо:
![]()
![]()
![]()
![]()
![]()
![]() якщо a і b – неколінеарні вектори, то для будь-якого вектора c існує розклад с = ma + nb, де m і n – деякі числа, до того ж такий розклад єдиний.
якщо a і b – неколінеарні вектори, то для будь-якого вектора c існує розклад с = ma + nb, де m і n – деякі числа, до того ж такий розклад єдиний.
![]()
![]()
![]()
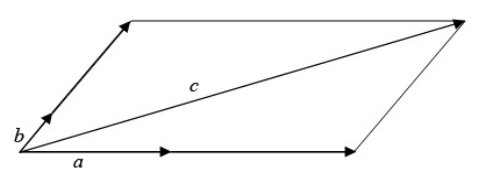
Рис.23
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() Якщо вектори a і b неколінеарні та для вектора с знайдено пару чисел (m ; n) таку, що с = ma + nb, то говорять, що вектор с розкладено за векторами a і b.
Якщо вектори a і b неколінеарні та для вектора с знайдено пару чисел (m ; n) таку, що с = ma + nb, то говорять, що вектор с розкладено за векторами a і b.
![]()
![]()
![]() Упорядковану пару (a ; b) неколінеарних векторів називають базисом.
Упорядковану пару (a ; b) неколінеарних векторів називають базисом.
![]()
![]()
![]()
![]()
![]()
![]() Якщо для вектора с виконується рівність с = ma + nb, то говорять, що векторс розкладено за базисом (a ; b).
Якщо для вектора с виконується рівність с = ma + nb, то говорять, що векторс розкладено за базисом (a ; b).
![]()
![]()
![]()
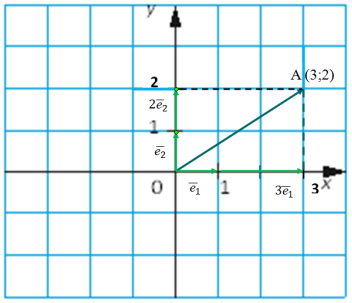 Упорядковану пару чисел (a ; b)називають координатами вектора с у базисі (a ; b).
Упорядковану пару чисел (a ; b)називають координатами вектора с у базисі (a ; b).
![]()

![]()

![]()
![]()
![]()
![]()
Рис. 24
![]()
![]()
![]()
![]() ОА =
ОА = ![]() ; ОА (3; 2);
; ОА (3; 2);
РОЗДІЛ 3
ПРАКТИЧНИЙ АСПЕКТ ТЕМИ «ВЕКТОРИ НА ПЛОЩИНІ»
3.1. Практичні завдання.
-



 Дано вектори a та b точки A і В (рис. 25 і рис. 26 відповідно). Відкладіть від точки A вектор, рівний вектору a та від точки В, вектор, рівний вектору b.
Дано вектори a та b точки A і В (рис. 25 і рис. 26 відповідно). Відкладіть від точки A вектор, рівний вектору a та від точки В, вектор, рівний вектору b.
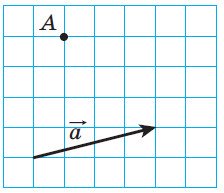
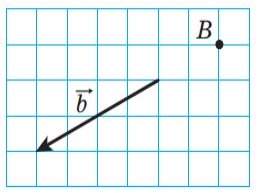
Рис. 25 Рис. 26
-

 За допомогою правила трикутника та правила паралелограма суму векторів a та b,зображених на рисунку:
За допомогою правила трикутника та правила паралелограма суму векторів a та b,зображених на рисунку:
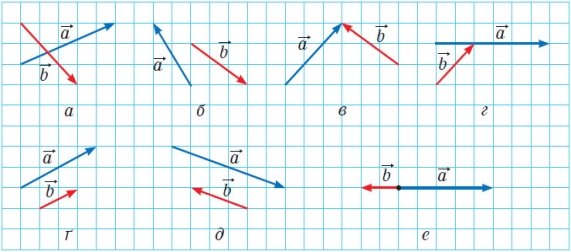
Рис.27
- За допомогою відповідного масштабу накресліть вектор, який зображає політ літака спочатку на 200 км на схід (з пункту А в пункт В), а потім на 300 км на південь (з пункту В у пункт С). Накресліть вектор, який зображає переміщення літака з початкової точки А у кінцеву точки С.
-






 Накресліть попарно колінеарні вектори a і b, c і d. Побудуйте суми
Накресліть попарно колінеарні вектори a і b, c і d. Побудуйте суми
![]()
![]()
![]()
![]() a +b, c +d, a +b+d.
a +b, c +d, a +b+d.
-





 Накресліть два ненульові вектори m і n. За допомогою циркуля і лінійки побудуйте вектори: a) m –n; b) n – m. Які вектори ви отримали?
Накресліть два ненульові вектори m і n. За допомогою циркуля і лінійки побудуйте вектори: a) m –n; b) n – m. Які вектори ви отримали?
-







 Дано вектори a і b. Побудуйте вектор: a) 2a + b; b)
Дано вектори a і b. Побудуйте вектор: a) 2a + b; b)  a + b; c) a-
a + b; c) a- b.
b.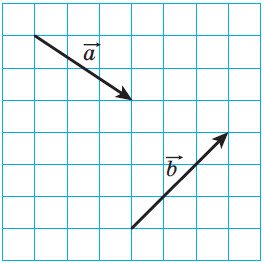
Рис.28
-
 Накресліть трикутник АВС. Позначте точку М – середину сторони АС. а) Від точки М відкладіть вектор, рівний вектору
Накресліть трикутник АВС. Позначте точку М – середину сторони АС. а) Від точки М відкладіть вектор, рівний вектору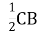 .
.
![]()
![]()
![]() b) Від точки М відкладіть вектор, рівний вектору
b) Від точки М відкладіть вектор, рівний вектору ![]() .
.
-
 Побудуйте кут, величина якого дорівнює куту між векторами a і b.
Побудуйте кут, величина якого дорівнює куту між векторами a і b. 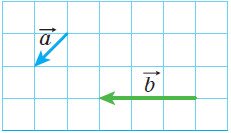
Рис. 29 -




 На рисунку зображено вектор a (довжина сторони клітинки 0,5 см). Відкладіть від точки A вектор b, такий, що | b|= 3 см і ∠( a;b )
На рисунку зображено вектор a (довжина сторони клітинки 0,5 см). Відкладіть від точки A вектор b, такий, що | b|= 3 см і ∠( a;b ) 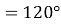 . Скільки розв’язків має задача?
. Скільки розв’язків має задача?
![]()
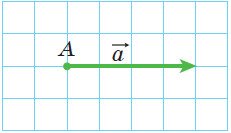
Рис. 30
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() 10)Накресліть три неколінеарні вектори a, b і c. За допомогою креслярських інструментів розкладіть вектор c за векторами a і b. Виміряйте довжини отриманих векторів, визначте відповідні коефіцієнти і запишіть вектор с через вектори a і b.
10)Накресліть три неколінеарні вектори a, b і c. За допомогою креслярських інструментів розкладіть вектор c за векторами a і b. Виміряйте довжини отриманих векторів, визначте відповідні коефіцієнти і запишіть вектор с через вектори a і b.
![]()
![]()
![]() 11) Накресліть два ненульових вектори m i n , які лежать на двох взаємно перпендикулярних прямих. Накресліть третій вектор l.
11) Накресліть два ненульових вектори m i n , які лежать на двох взаємно перпендикулярних прямих. Накресліть третій вектор l.
![]()
![]()
![]()
![]()
![]()
![]() Розкладіть (побудовою) вектор l за векторами m i n. Визначте відповідні коефіцієнти і запишіть вектор l через вектори m i n.
Розкладіть (побудовою) вектор l за векторами m i n. Визначте відповідні коефіцієнти і запишіть вектор l через вектори m i n.
![]()
![]()
![]() 12)Побудуйте довільний трикутник АВС і проведіть його медіану АМ. Розкладіть (побудовою) вектор АМ за векторами АВ і АС. Запишіть відповідний вираз.
12)Побудуйте довільний трикутник АВС і проведіть його медіану АМ. Розкладіть (побудовою) вектор АМ за векторами АВ і АС. Запишіть відповідний вираз.
3.2. Вправи.
1) Які з векторів, зображених на рисунку 31:
a) рівні; c) протилежно напрямлені;
b) співнапрямлені; d)колінеарні?
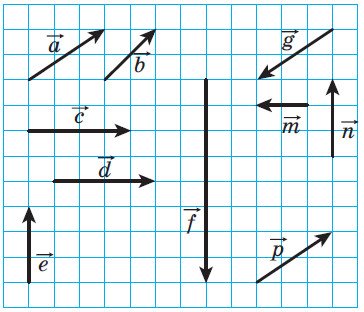
Рис.31
2)Координати вектора (встановіть відповідність):
-
 А(1;2) і В(-3;-4); А) АВ(-4;6);
А(1;2) і В(-3;-4); А) АВ(-4;6);
-
 А(1;-2) і В(-3;4); Б) АВ(-4;-6);
А(1;-2) і В(-3;4); Б) АВ(-4;-6);
-
 А(-1;-2) і В(3;4); В) АВ(2;2);
А(-1;-2) і В(3;4); В) АВ(2;2);
-
 А(1;2) і В(3;4); Г) АВ(4;6);
А(1;2) і В(3;4); Г) АВ(4;6);
![]() е) А(-1;-2) і В(-3;-4); Д) АВ(-2;-2).
е) А(-1;-2) і В(-3;-4); Д) АВ(-2;-2).
3)Знайдіть координати векторів, зображених на рисунку 32:
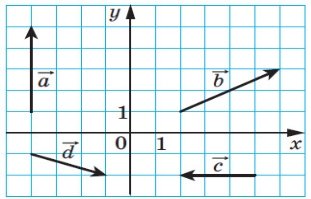
Рис.32
4)Вектори(тестові завдання).
- Чи можуть два колінеарні вектори не бути співнапрямленими ?
А) ні Б) так В) немає правильної відповіді Г) не знаю
- Чи можуть два протилежно напрямлені вектори не бути колінеарними ? А) ні Б) так В) немає правильної відповіді Г) не знаю
- Чи можуть початки і кінці двох неколінеарних векторів бути вершинами паралелограма ?
А) ні Б) так В) немає правильної відповіді Г) не знаю
- Чи можуть початки і кінці двох неколінеарних векторів бути вершинами трапеції? А) ні Б) так В) немає правильної відповіді Г) не знаю
- Чи може довжина вектора-суми бути меншою за довжину кожного з векторів-доданків? А) ні Б) так В) немає правильної відповіді Г) не знаю
- Чи може довжина вектора-різниці бути більшою за довжину кожного з векторів,різницю яких знаходять? А) ні Б) так В) немає правильної відповіді Г) не знаю
-








 Для ненульових векторів a, b і c справджуються рівності a ∙b=0 і b ∙c=0. Чи правильно,що a ∙ c=0? А) ні Б) так В) немає правильної відповіді Г) не знаю
Для ненульових векторів a, b і c справджуються рівності a ∙b=0 і b ∙c=0. Чи правильно,що a ∙ c=0? А) ні Б) так В) немає правильної відповіді Г) не знаю
-






 Для ненульових векторів a, b і c справджуються рівності a ∙b=0 і b ∙c=0. Чи колінеарні вектори? А) ні Б) так В) немає правильної відповіді Г) не знаю
Для ненульових векторів a, b і c справджуються рівності a ∙b=0 і b ∙c=0. Чи колінеарні вектори? А) ні Б) так В) немає правильної відповіді Г) не знаю
-








 Який вектор треба поставити у вираз АВ+ВС+Х = ОD - ОА замість Х, щоб отримати правильну рівність? А) СВ Б) АD В) СD Г) АС
Який вектор треба поставити у вираз АВ+ВС+Х = ОD - ОА замість Х, щоб отримати правильну рівність? А) СВ Б) АD В) СD Г) АС
-


 Дано точки М(2;-1),N(-2;4), K(3;7). Знайдіть координати точки Р такої, що сума векторів MN+KP=0
Дано точки М(2;-1),N(-2;4), K(3;7). Знайдіть координати точки Р такої, що сума векторів MN+KP=0
- Вектори. Формули (знайдіть пару):
-


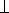

 а b; 1)
а b; 1) 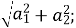
-




 k ∙ а; 2) a ∙ b=0;
k ∙ а; 2) a ∙ b=0;
-

 a=b; 3) (k
a=b; 3) (k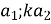 );
);
-



 a b; 4)
a b; 4)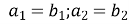 ;
;
-

 l a l; 5)
l a l; 5) 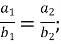
-

 a ∙ b; 6) (
a ∙ b; 6) (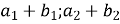 );
);
-
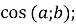 7) l al ∙ l b l ∙
7) l al ∙ l b l ∙ 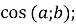
-

 a + b; 8)
a + b; 8)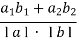
- Доведіть, що чотирикутник ABCD з вершинами в точках A (1; –5), B (2; 3), A (1; –5), B (2; 3), C (–3; 1) і D (–4; –7) є паралелограмом..
- Скалярний добуток векторів (заповніть пропуски):
-

 Скалярним добутком двох векторів a i b буде ……… , що дорівнює добутку модулів цих векторів, помножене на косинус кута між ними.
Скалярним добутком двох векторів a i b буде ……… , що дорівнює добутку модулів цих векторів, помножене на косинус кута між ними.
- Якщо вектори співнапрямлені , то кут між векторами дорівнює……....
- Косинус кута в 0° дорівнює ………………………………………………
- Скалярний добуток вектора самого на себе дорівнює …………………...
-

 Якщо a(xa;ya) i b(xb;yb), то ………………………………………………...
Якщо a(xa;ya) i b(xb;yb), то ………………………………………………...
- Якщо вектори протилежно напрямлені, то кут між векторами дорівнює……………………………………………………………………. .
- Скалярний добуток перпендикулярних векторів дорівнює………………
- Для визначення кута між векторами, потрібно їх…………………….…...
Варіанти відповідей: 0
1
180°
квадрату його модуля
нулю градусів
розмістити в спільній початковій точці
![]() число
число
![]() a ∙ b= xa ∙ xb+ ya ∙ yb
a ∙ b= xa ∙ xb+ ya ∙ yb
3.3. Розв’язування геометричних задач векторним способом.
Під час розв’язування геометричних задач векторним способом доцільно користуватися такою схемою:
- сформулювати задачу мовою векторів;
- увести прямокутну систему координат або вибрати два неколінеарних вектори на площині як основні (базисні), а також ввести допоміжні вектори;
- скласти відповідні до умови задачі векторні рівності та перетворити їх на підставі відомих векторних співвідношень;
- перекласти одержані результати мовою геометрії.
3.4. Застосування векторів до розв’язування задач.
![]()
![]()
![]()
![]() 1) Виразіть вектор АВ через вектори a, b, c і d (рис.33.)
1) Виразіть вектор АВ через вектори a, b, c і d (рис.33.)
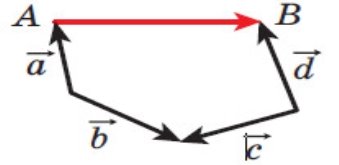
Рис.33
![]()
![]()
![]()
![]()
![]() 2) Доведіть, що для будь-яких точок A, B, C, D і E виконується рівність AB+ BC+ CD+ DE+ EA=0.
2) Доведіть, що для будь-яких точок A, B, C, D і E виконується рівність AB+ BC+ CD+ DE+ EA=0.
![]()
![]() 3) Доведіть, що коли OA= kOB, то точки O, A і B лежать на одній прямій.
3) Доведіть, що коли OA= kOB, то точки O, A і B лежать на одній прямій.
![]()
![]() Р о з в ’я з а н н я. З умови випливає, що вектори OA і OB колінеарні. До того ж ці вектори відкладено від однієї точки O. Отже, точки O, A і B лежать на одній прямій.
Р о з в ’я з а н н я. З умови випливає, що вектори OA і OB колінеарні. До того ж ці вектори відкладено від однієї точки O. Отже, точки O, A і B лежать на одній прямій.
![]()
![]()
![]() 4)Точка M — середина відрізка AB і X — довільна точка (рис 34.). Доведіть, що XM =
4)Точка M — середина відрізка AB і X — довільна точка (рис 34.). Доведіть, що XM =![]() XA+ XB).
XA+ XB).
Р о з в ’я з а н н я. Застосовуючи правило трикутника, запишемо:
![]()
![]()
![]() XM = XA + AM;
XM = XA + AM;
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() XM = XB + BM.
XM = XB + BM.
Додамо ці дві рівності: 2XM= XA+ XB+ AM+ BM. Оскільки вектори
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() AM і BM протилежні, то AM + BM=0. Маємо: 2XM= XA+ XB.
AM і BM протилежні, то AM + BM=0. Маємо: 2XM= XA+ XB.
![]()
![]()
![]() Звідси XM=
Звідси XM= ![]() (XA+ XB), що й треба було довести.
(XA+ XB), що й треба було довести.
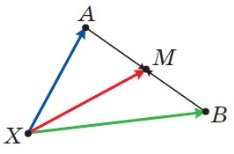
Рис.34
5)Доведіть, що середини основ трапеції та точка перетину продовжень її бічних сторін лежать на одній прямій.
Р о з в ’я з а н н я. Нехай точки M і N — середини основ BC і AD трапеції
ABCD, O — точка перетину прямих AB і CD (рис.35). Застосовуючи ключову
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() задачу 4), запишемо: OM =
задачу 4), запишемо: OM =![]() ( OB+ OC), ON=
( OB+ OC), ON=![]() ( OA+ OD). Оскільки OB║OA і OC║OD, то OB= k∙OAі OC= k∙ OD . де k і k1 — деякі числа. Оскільки ∆BOC подібний ∆AOD, то
( OA+ OD). Оскільки OB║OA і OC║OD, то OB= k∙OAі OC= k∙ OD . де k і k1 — деякі числа. Оскільки ∆BOC подібний ∆AOD, то ![]() =
=![]() .Отже, k =
.Отже, k = ![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() Маємо: OM =
Маємо: OM =![]() OB + OC) =
OB + OC) =![]() k ∙ OA + k ∙ OD) = k ∙
k ∙ OA + k ∙ OD) = k ∙ ![]() OA + OD) = k
OA + OD) = k![]()
Із ключової задачі 3) випливає, що точки O, M і N лежать на одній прямій, щой треба було довести.
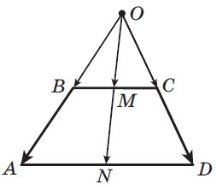
Рис.35
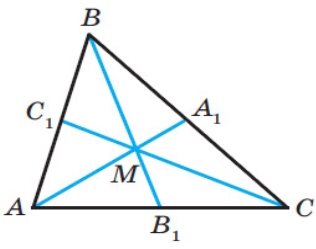
6)Медіанитрикутника ABC перетинаються в точці M.
![]()
![]()
![]()
![]() Доведіть, що MA + MB + MC = 0.
Доведіть, що MA + MB + MC = 0.
Рис.36
Р о з в ’я з а н н я. Нехай відрізки A![]() , B
, B![]() і C
і C![]() — медіани трикутника ABC (рис. 36). Застосовуючи ключову задачу4), запишемо:
— медіани трикутника ABC (рис. 36). Застосовуючи ключову задачу4), запишемо:
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() A
A![]() =
= ![]() (AB + AC);
(AB + AC);![]() =
= ![]() (ВA + ВC); С
(ВA + ВC); С![]() =
= ![]() (СВ + CА).
(СВ + CА).
Додавши ліві і праві частини одержаних рівностей, маємо:
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() A
A![]() +
+ ![]() + С
+ С![]() =
= ![]() AB + AC + ВA + ВC + СВ + CА) =
AB + AC + ВA + ВC + СВ + CА) =
![]()
![]()
![]()
![]()
![]()
![]() =
=![]() AB + ВA + ВC + СВ + AC + CА) = 0.
AB + ВA + ВC + СВ + AC + CА) = 0.
![]()
![]() Із властивості медіан трикутника випливає, що AM =
Із властивості медіан трикутника випливає, що AM = ![]() A
A![]()
![]()
![]()
![]()
![]()
![]()
![]() Тоді MА = -
Тоді MА = - ![]() A
A![]() Аналогічно MB = -
Аналогічно MB = -![]() , MC = -
, MC = - ![]() С
С![]() .
.
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() Звідси MA + MB + MC = -
Звідси MA + MB + MC = - ![]() A
A![]() -
-![]() -
- ![]() С
С![]() = -
= - ![]() (A
(A![]() +
+ ![]() + С
+ С![]() ) = 0, що й треба було довести.
) = 0, що й треба було довести.
![]()
![]()
 І н ш и й с п о с і б р о з в ’я з а н н я.
І н ш и й с п о с і б р о з в ’я з а н н я.
Виконаємо додаткову побудову. Відкладемо ![]() , що дорівнює М
, що дорівнює М![]() .
.
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() Одержаний чотирикутник МВDС – паралелограм (М
Одержаний чотирикутник МВDС – паралелограм (М![]() за побудовою,
за побудовою,![]() за умовою). Тоді МВ + МС = МD, але МD = - DМ, тобто МВ + МС = - DМ. Отже, МВ + МС +DМ = 0. Враховуючи, те,що М
за умовою). Тоді МВ + МС = МD, але МD = - DМ, тобто МВ + МС = - DМ. Отже, МВ + МС +DМ = 0. Враховуючи, те,що М![]() за побудовою і властивість медіан трикутника, маємо:
за побудовою і властивість медіан трикутника, маємо:
![]()
![]() DМ = МА. Отже, що й треба було довести, що й треба було довести.
DМ = МА. Отже, що й треба було довести, що й треба було довести.
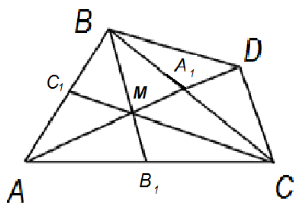
Рис.37
![]()
![]() 7) Назвіть координати векторів (встановіть відповідність):
7) Назвіть координати векторів (встановіть відповідність):
![]() a) a=2b+6c; 1) (1; 3);
a) a=2b+6c; 1) (1; 3);
![]()
![]()
![]() b) k = c+3d; 2) (-2; 6);
b) k = c+3d; 2) (-2; 6);
![]()
![]() c) b = -3k; 3) (-5; 0);
c) b = -3k; 3) (-5; 0);
![]()
![]() d) c = -5a;. 4) (0; -3).
d) c = -5a;. 4) (0; -3).
3.5. Завдання для перевірки знань
1) Завдання для повторення теми «Вектори на площині».
- Наведіть приклади векторних і скалярних величин.
- Які вектори називають колінеарними?
- Що таке модуль вектора?
- Чи завжди є правильним твердження: «Якщо модулі двох векторів рівні, то ці вектори рівні»? Наведіть приклади.
- Чим відрізняються протилежно напрямлені вектори? Наведіть приклад.
- Наведіть приклад: a) співнапрямлених векторів;
b) протилежно напрямлених векторів;
c) рівних векторів.
7. Сформулюйте означення рівності векторів.
8. Наведіть приклад множення одного й того самого вектора на число:
a) 2; b) -2. Чи будуть рівними модулі цих векторів?
9. Наведіть приклади додавання двох колінеарних:
a) однаково напрямлених векторів;
b) протилежно напрямлених векторів.
10. Наведіть приклади віднімання двох колінеарних:
a) однаково напрямлених векторів;
b) протилежно напрямлених векторів.
11. Наведіть приклади: a) додавання двох неколінеарних векторів;
b) віднімання двох неколінеарних векторів.
![]()
![]() 12. Дано паралелограм КМНР. Знайдіть:
12. Дано паралелограм КМНР. Знайдіть:
a) різницю векторів КМ і РН;
![]()
![]()
![]()
![]()
![]()
![]() b) суму векторів КМ і НР.
b) суму векторів КМ і НР.
13. Дано чотирикутник ABCD. Знайдіть суму векторів AB, BC, CD, DA.
![]() 14. Дано паралелограм CМЕT. Розкладіть вектор СЕ за векторами:
14. Дано паралелограм CМЕT. Розкладіть вектор СЕ за векторами:
![]()
![]()
![]()
![]()
![]()
![]() a) CМ і СТ; b) МС і ТС; c) МС і СТ.
a) CМ і СТ; b) МС і ТС; c) МС і СТ.
![]()
![]()
![]()
![]()
![]()
![]() 15. Діагоналі паралелограма ABCD перетинаються в точці О. Розкладіть за векторами AB і CD вектори:
15. Діагоналі паралелограма ABCD перетинаються в точці О. Розкладіть за векторами AB і CD вектори:
a) ОА; b) ОС; c) ВD; d) ОВ.
![]()
![]() 16. На рис.38 дано вектори a і b. Побудуйте вектори:
16. На рис.38 дано вектори a і b. Побудуйте вектори:
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() a) a + b; b) a - b; c) a + 0,5b; d) b – 0,5a.
a) a + b; b) a - b; c) a + 0,5b; d) b – 0,5a.
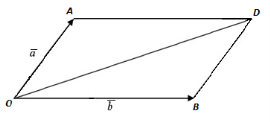
Рис.38
2) Тестові завдання.
1. В якому році вперше з’явився термін «вектор»?
А) 1844; Б) 1850; В) 1845; Г) 1854.
2. Якщо будь-яка точка площини є вектором, то як вона називається?
А) Простий вектор Б) Одиничний вектор
В) Точковий вектор Г) Нульовий вектор
3.Скільки векторів можна відкласти від будь-якої точки, що дорівнює даному вектору?
А) Нескінченно багато. Б) Ні одного
В) Два вектори Г) Тільки один
4. Діагоналлю якої геометричної фігури є вектор-сума?
А) Трапеції Б) Паралелограма
В) Круга Г) Трикутника
5. Яка величина не є векторною?
А) Прискорення Б) Імпульс В) Сила. Г) Робота.
![]()
![]()
![]() 6. При якому значенні n вектори p(4; 2n –1) і m(4; 9 – 3n) рівні?
6. При якому значенні n вектори p(4; 2n –1) і m(4; 9 – 3n) рівні?
А) 0,5; Б) 2; В) 8; Г) 10.
3) Завдання «Перевірте себе».
1.Яка з наведених величин є векторною?
А) Час; Б)швидкість; В) об’єм; Г) маса.
2.Чому дорівнює модуль вектора, початок і кінець якого збігаються?
А) 0; Б) 1; В) – 5; Г) –1.
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() 3.Дано паралелограм ABCD. Яка з даних рівностей є правильною?
3.Дано паралелограм ABCD. Яка з даних рівностей є правильною?
А) AC=BD ; Б) BC=DA; В) AB=C D; Г) AB= DC.
![]()
![]() 4.Відомо, що AM = MB. Яке з даних тверджень є правильним?
4.Відомо, що AM = MB. Яке з даних тверджень є правильним?
А) точка A— середина відрізка AM;
Б) точка M— середина відрізка MB;
В) точка B— середина відрізка AB;
Г) точка M — вершина трикутника AMB.
5.Дано точки A (–2; 3) і B (2; –1). Точка M — середина відрізка AB.
![]() Знайдіть координати вектора AM.
Знайдіть координати вектора AM.
А) (0; –1); Б) (–1; 0); В) (0; 1); Г) (1; 0).
![]()
![]() 6. При якому значенні х вектори a(6; х) і b(-3;1) колінеарні?
6. При якому значенні х вектори a(6; х) і b(-3;1) колінеарні?
А) 2; Б) – 2; В) –1 ; Г) 1.
![]()
![]()
![]()
![]()
![]()
![]() 7. Яка з даних рівностей є правильною?
7. Яка з даних рівностей є правильною?
![]()
![]()
![]()
![]()
![]()
![]()
![]() А) AM + AN= MN; Б) MA – MA= AM;
А) AM + AN= MN; Б) MA – MA= AM;
В) MA+ AN + AN= MN; Г) MA + AN = MN.
![]()
![]() 8. Дано вектор a (-1;
8. Дано вектор a (-1;![]() ). Який з векторів дорівнює вектору
). Який з векторів дорівнює вектору ![]() a ?
a ?
![]()
![]() А) с (-
А) с (-![]() ); Б) m (-
); Б) m (-![]() )
)
![]()
![]() В) n (2
В) n (2![]() ); Г) p (1
); Г) p (1![]() )
)
![]()
![]() 9. Дано вектори m (-4;1) і n (3;-2). Знайти координати вектора
9. Дано вектори m (-4;1) і n (3;-2). Знайти координати вектора
![]()
![]()
![]() p = -3m+4 n.
p = -3m+4 n.
![]()
![]() А) p (-11;24 ); Б) p (12;-3)
А) p (-11;24 ); Б) p (12;-3)
![]()
![]() В) p (24;-11) Г) p (12;-8).
В) p (24;-11) Г) p (12;-8).
![]()
![]() 10. Знайдіть скалярний добуток векторів a(5;-2) і b(1;3).
10. Знайдіть скалярний добуток векторів a(5;-2) і b(1;3).
А) 0; Б) 11; В) 1 ; Г) -1.
![]()
![]() 11. При якому значенні х вектори a (х;-2) і b(4;1) перпендикулярні.
11. При якому значенні х вектори a (х;-2) і b(4;1) перпендикулярні.
А) ![]() ; Б) 2; В) -1 ; Г) 1.
; Б) 2; В) -1 ; Г) 1.
![]()
![]() 12. Дано точки Р(–1;0), А (-3; –2), T(1; 4). Обчислити косинус кута між векторами AP і AT:
12. Дано точки Р(–1;0), А (-3; –2), T(1; 4). Обчислити косинус кута між векторами AP і AT:
А) ![]() ; Б)
; Б)![]() ; В)
; В) ![]() ; Г)
; Г)![]() .
.
13. У прямокутному рівнобедреному трикутнику з бічною стороною
![]()
![]() 2 см проведено медіану з вершини гострого кута. Задайте координатні вектори
2 см проведено медіану з вершини гострого кута. Задайте координатні вектори ![]()
![]() та обчисліть косинус кута між медіаною та гіпотенузою.
та обчисліть косинус кута між медіаною та гіпотенузою.
А) ![]() ; Б)
; Б)![]() ; В)
; В)![]() ; Г)
; Г)![]() .
.
СПИСОК ВИКОРИСТАНИХ ДЖЕРЕЛ
- Г.В. Апостолова. Геометрія, 8 клас. Дворівневий підручник для загальноосвітніх навчальних закладів . – Київ: Генеза, 2008.
- М.І. Бурда, Л.М. Савченко. Геометрія. Навчальний посібник для 8 – 9 класів з поглибленим вивченням. – Київ: Освіта, 1996
- О.С. Істер. Геометрія, 9 клас. Підручник для загальноосвітніх навчальних закладів . – Київ : Генеза, 2017.
- А.Г. Мерзляк, В.Б. Полонський, М.С. Якір .Геометрія, 9 клас. Підручник для загальноосвітніх навчальних закладів з поглибленим вивченням математики. – Харків : Гімназія , 2017.
- Лариса Олійник. Геометричний тренажер. 9 клас. – Тернопіль : Підручники і посібники, 2017
- В.Б. Полонський, Ю.М. Рабінович, М.С. Якір. Вчимося розв’язувати задачі з геометрії. Навчально-методичний посібник. – Тернопіль: Підручники і посібники, 2002
- Програми для загальноосвітніх навчальних закладів (http://mon.gov.ua/activity/education/zagalna-serednya/navchalni-programy.html)
ДОДАТКИ
Додаток 1
Історична довідка
Даний матеріал містить історичні відомості про витоки числення з напрямленими відрізками.
Термін «вектор» (від латинського слова Vector, що в перекладі означає «несучий» або «той, що несе») вперше з’явився у1845 році в роботах по побудові числових систем ірландського математика У. Гамільтона (1805-1865), а також зустрічається в роботах німецького математика ХІХ століття Г. Грассмана.


У. Гамільтон (1805-1865) Г. Грассмана (1809 -1877 )
![]() Поняття вектора було охоче сприйняте багатьма математиками і фізиками. Позначення
Поняття вектора було охоче сприйняте багатьма математиками і фізиками. Позначення ![]() для напрямленого відрізка вперше використав у 1806 р. швейцарський математик Ж. Арган (1768-1822р.). Починаючи з 1853 року вектор стали позначати однією буквою a, як це зробив французький математик О.Коші (1789-1857).
для напрямленого відрізка вперше використав у 1806 р. швейцарський математик Ж. Арган (1768-1822р.). Починаючи з 1853 року вектор стали позначати однією буквою a, як це зробив французький математик О.Коші (1789-1857).


Ж. Арган (1768-1822) О. Коші (1789-1857)
Додаток 2
Застосування векторів у фізиці
Основні напрями використання векторів при вивченні фізики
Найбільше вектори використовуються:
1) в класичній механіці: для визначення положення тіла, швидкості, прискорення, сили, імпульсу тіла, моментів сили та імпульсу, в задачах на рух під дією кількох сил (зокрема: знаходження рівнодійної сили при умові, коли вектори співнапрямлені, протилежно напрямлені та знаходяться під кутом);
2) в теорії відносності;
3) в електродинаміці: напруженість електричного та магнітних полів, магнітна індукція.
![]()
![]() Використання правила паралелограма:
Використання правила паралелограма:
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() досвід показує, що одночасна дія двох сил F1 та F2 дорівнює дії однієї сили F, яка є діагоналлю паралелограма, побудованого на векторах F1 та F2. Ця сила F має назву рівнодійної (або результуючої) двох сил F1 та F2 і дорівнює F=F1+F2. В даному випадку застосовується правило паралелограма для суми двох довільних векторів. Це правило використовується для обчислення суми сил, швидкості, прискорення, напруженості поля.
досвід показує, що одночасна дія двох сил F1 та F2 дорівнює дії однієї сили F, яка є діагоналлю паралелограма, побудованого на векторах F1 та F2. Ця сила F має назву рівнодійної (або результуючої) двох сил F1 та F2 і дорівнює F=F1+F2. В даному випадку застосовується правило паралелограма для суми двох довільних векторів. Це правило використовується для обчислення суми сил, швидкості, прискорення, напруженості поля.
Використання правила трикутника:
якщо вектори колінеарні, то краще використати правило трикутника.
Використання скалярного добутку:
![]()
![]()
![]()
![]()
![]() скалярний добуток двох векторів застосовується в задачах на обчислення роботи: робота дорівнює скалярному добутку вектора сили F на вектор переміщення S, тобто A = F⋅ S або A = F⋅ S⋅cos α.
скалярний добуток двох векторів застосовується в задачах на обчислення роботи: робота дорівнює скалярному добутку вектора сили F на вектор переміщення S, тобто A = F⋅ S або A = F⋅ S⋅cos α.
Використання векторів при вивченні законів Ньютона
Перший закон Ньютона. Якщо на тіло не діють інші тіла або їх дія скомпенсована, то дане тіло зберігає стан спокою або рівномірного руху.
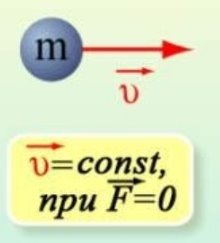
Другий закон Ньютона. Прискорення, набуте матеріальною точкою або тілом, пропорційне рівнодійній всіх діючих сил і обернено пропорційне масі матеріальної точки або тіла.

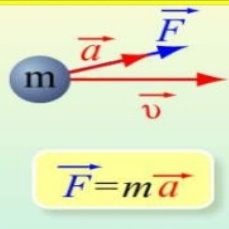
![]() Вага тіла P= mg
Вага тіла P= mg
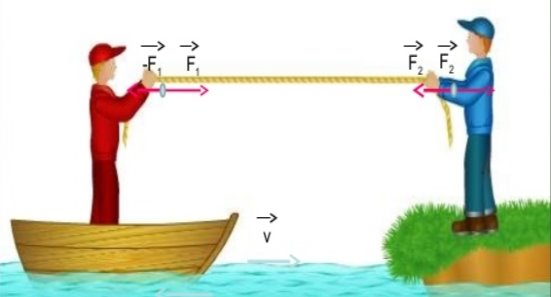
Третій закон Ньютона. Сили, з якими взаємодіють тіла або матеріальні точки, завжди рівні за модулем й протилежні за напрямком.
![]()
![]()
![]()
![]()
Fопору
Задачі з фізики з використанням векторів
Задача 1.
Група туристів вирішила прогулятися вздовж річки. Спочатку вони йшли в південному напрямі 300 м, потім після того, як вони перетнули міст, вирушили в південно-східному напрямі вздовж річки і пройшли ще 200 м. Яке переміщення здійснили туристи? Який шлях пройшли?
Задача 2.
Дано три сили: ![]()
![]()
![]() , прикладені до однієї точки. Обчислити роботу, яку виконує рівнодійна цих сил, коли точка їх прикладання, рухаючись прямолінійно, переміщується з точки A(5;3) в точку B(4;-1).
, прикладені до однієї точки. Обчислити роботу, яку виконує рівнодійна цих сил, коли точка їх прикладання, рухаючись прямолінійно, переміщується з точки A(5;3) в точку B(4;-1).
Розв'язання. Обчислимо силу F, яка є рівнодійною сил : ![]() ,
,![]() ,
, ![]() , тобто
, тобто
F=![]()
![]() , F(2;
, F(2;![]() 3). Знаходимо вектор переміщення AB(
3). Знаходимо вектор переміщення AB(![]() 1;
1;![]() ) і обчислюємо роботу: A = F ⋅ AB =
) і обчислюємо роботу: A = F ⋅ AB = ![]() +12 = 10(од. роботи).
+12 = 10(од. роботи).
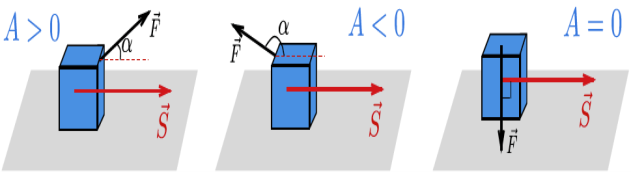
Робота з перемiщення тiла залежить вiд кута мiж вектором перемiщення та прикладеною силою.
Таким чином:
1) якщо проекцiя сили на вiсь, спрямовану вздовж перемiщення, додатня (0° < α < 90°, cos α > 0), то i робота, яку виконано, має знак «+»;
2) якщо проекцiя прикладеної сили на вiсь вiд’ємна (90°< α <180°,
сos α < 0), то i робота – вiд’ємна;
- робота з перемiщення тiла може бути i нульова: в тому випадку, коли кут мiж вектором перемiщення та прикладеною силою становить .
Задача 3.
Ящик масою m=30кг протягнули на вiдстань 30 м, прикладаючи силу F=30 Н пiд кутом 30° до горизонту. Сила тертя Fт=20Н.
1. Яку роботу з перемiщення ящика виконує сила F?
2. Яку роботу з перемiщення ящика виконує сила тертя Fт?
3. Яку саме потрiбно прикласти силу F, щоб її робота дорiвнювала нулеві?
Розв’язання.
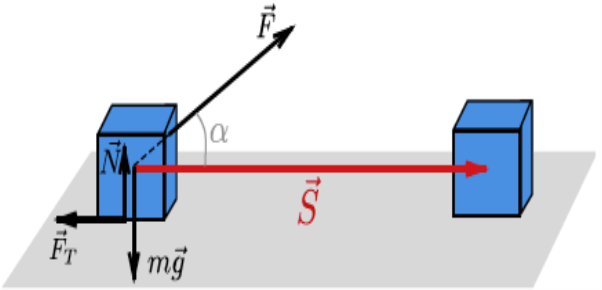
- Сила F спрямована пiд кутом 30° до вектора перемiщення S.
Робота: A=F⋅S⋅ cos α=30⋅30⋅ √3/2≈765(Дж)
2. Сила тертя спрямована в протилежному напрямку від вектора перемiщення. Отже, вона виконує вiд’ємну роботу, тобто кут α=180°, а, отже, cosα=1. Робота: Aт = −F⋅ S = −20⋅30 = −600(Дж).
3. Щоб робота сили F дорiвнювала нулеві, тобто щоб ящик не рухався вздовж горизонтальної поверхнi, очевидно, що силу небхідно прикласти пiд прямим кутом до горизонту.
Задача 4.
Тіло кинуто під кутом 60° до горизонту із швидкістю 20 м/с. Визначити швидкість тіла через 2 с, а також модуль його переміщення за цей інтервал часу.
Задача 5.
Автомобіль масою 5 т рухається рівномірно вгору. Визначте силу тяги, яку розвиває двигун, якщо коефіцієнт тертя дорівнює 0,7, а кут підйому 30°, g=10 м/с2 .
Додаток 3
Вектори навколо нас
Вектор є доказом того, що математика
може зображати не тільки стан, а й процес: рух
(Енгельс)
Уперше поняття вектора як напрямленого відрізка знайшло застосування в механіці для зображення фізичних векторних величин: швидкості, прискорення, сили, моменту сили тощо.
Високий ступінь наочності і простота геометричних операцій над векторами як напрямленими відрізками сприяли тому, що поняття вектора знайшло загальне визнання і застосування в інших розділах фізики: в кінематиці, статиці, динаміці точки і динаміці системи,в теорії відносності, в теорії потенціалу та гідродинаміці. Також стало одним із основних понять таких наук, як векторна алгебра, векторний аналіз, теорія поля.
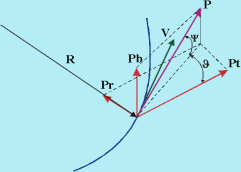
Поняття вектора виникає там, де доводиться мати справу з об’єктами, які характеризуються величиною і напрямом. Наприклад, швидкість, переміщення, сила, імпульс, тиск, магнітне поле. Такі величини називають векторними величинами або векторами. Магнітне поле — особлива форма матерії, за допомогою якої здійснюється взаємодія між рухомими електрично зарядженими частинками. Магнітне поле є векторним полем, тобто з кожною точкою простору пов'язаний векто р магнітної індукції
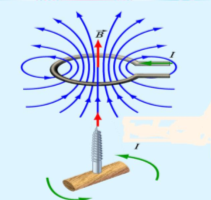
Переміщення – вектор, який характеризує зміну положення фізичного тіла.



Без знань про вектори неможливо займатись машинобудуванням, неможливо стати конструктором. Існує багато сфер життя, в яких використовуються знання про вектор.
На запитання «Для чого вивчати математику?» чудово відповів ще в ХІІІ столітті англійський філософ Роджер Бекон: «Той, хто не знає математики, не може пізнати іншої науки й навіть не може виявити свого неуцтва!».
1


про публікацію авторської розробки
Додати розробку
