Відеопрезентація: "Пропорційність відрізків хорд"
Про матеріал
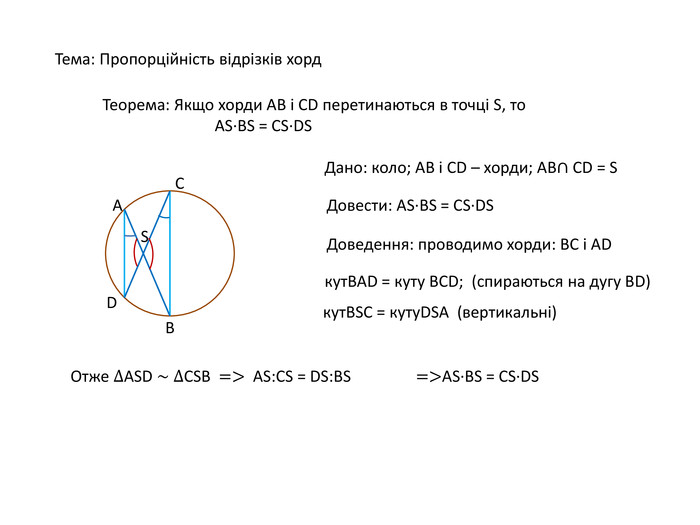
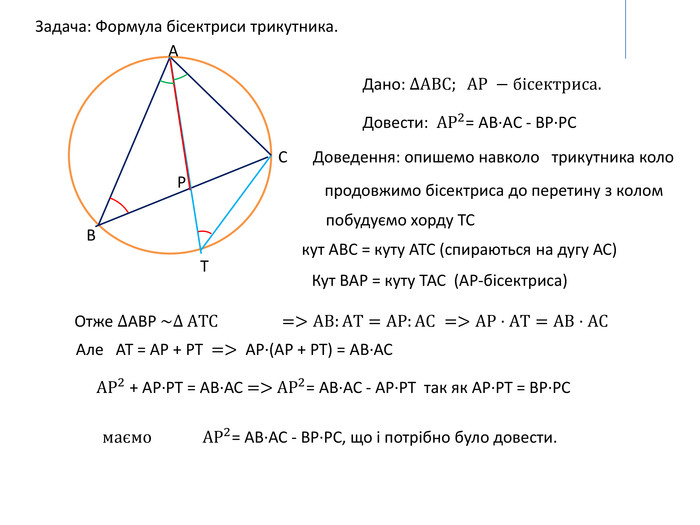
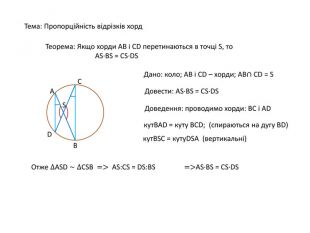
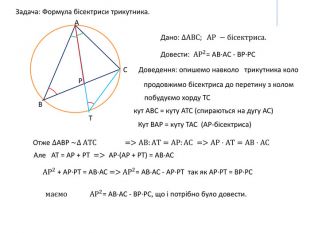
Відео, в якому показано доведення теореми про пропорційність відрізків хорд. Описано наслідки з цієї теореми. Виведено формулу для знаходження бісектриси трикутника.
Відео можна використовувати на уроках геометрії у 8 класі при вивченні розділу: "Подібність трикутників" за програмою стандарт.
Перегляд файлу
Зміст слайдів
pptx
Оцінка розробки


Безкоштовний сертифікат
про публікацію авторської розробки
про публікацію авторської розробки
Щоб отримати, додайте розробку
Додати розробку