Презентація: "Приклади розв'язування задач по темі: "Теорема Піфагора""
Про матеріал
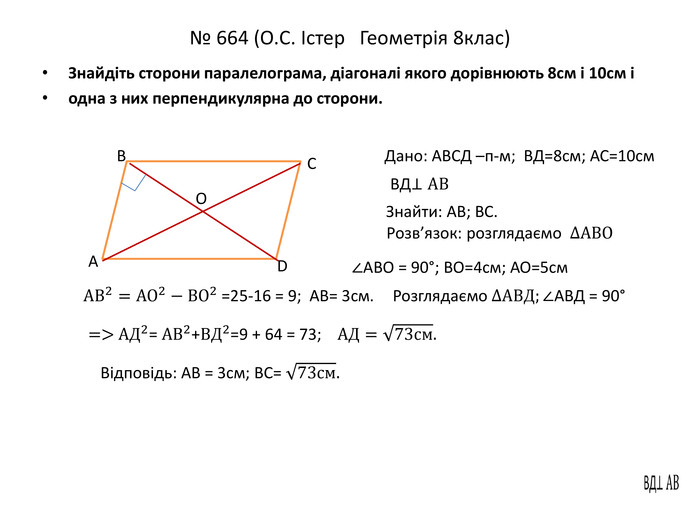
В презентації показано приклади розв'язування задач з теми "Теорема Піфагора" за підручником О.С. Істер "Геометрія 8 клас". Особливу увагу приділено порядку оформлення розв'язку задач з геометрії.
Перегляд файлу
Зміст слайдів
pptx
Оцінка розробки


Безкоштовний сертифікат
про публікацію авторської розробки
про публікацію авторської розробки
Щоб отримати, додайте розробку
Додати розробку