Відкритий урок"В царстві квадратних коренів"

 В царстве  квадратных  корней

Цели урока: 

Образовательные:

• организовать деятельность учащихся по систематизации и расширению знаний учащихся о свойствах квадратных корней и их применению;
• показать, как используются квадратные корни при решении задач физического, экономического, географического содержания,

Развивающие:

• Способствовать развитию вычислительных навыков;
• Развить познавательную активность, положительную мотивацию к предмету.
• Развивать потребности к самообразованию, умения искать и познавать информацию
• Развивать умение учащихся работать индивидуально (самостоятельно), в группах и коллективно;
•  Развивать умение оценить свои силы, используя задания разного уровня сложности

Воспитательные:

• привитие интереса к математике;
• воспитание познавательной активности, умения общаться, общей культуры.

Оборудование. Интерактивная презентация PowerPoint,проектор. 

Smart-цель: формирование системы знаний по теме через практическое применение новых приемов и методов обучения.

 

Задачи:

 

• включить каждого школьника в осознанную учебную деятельность;
• создать для каждого школьника режим наибольшего благоприятствования (предоставление ему возможности продвигаться в изучении материала в оптимальном для себя темпе);
• сформировать у каждого ученика навыки самоконтроля.

 

Форма организации деятельности учащихся на уроке:

 фронтальная, индивидуальная, групповая, с использованием  АМО.

Методы и технологии, используемые на уроке:  проблемно-поисковые, ИКТ, дифференцированные, групповые, разноуровневые , игровые

Оборудование:

• презентация урока;
• плакаты для оформления доски: с девизом урока, с цитатами, 
• листы оценивания, карточки  лото  ,
• набор для  кластера, ромашка Блума
• листы ватмана, маркеры, магнитики. На доске в разных местах прикреплены пословицы:

• Набирайся ума в ученье, храбрости в сраженье.
• Без муки нет науки.
• Была бы охота – заладится, всякая работа.
• Математика – гимнастика ума.

•  

 

 

 

 

Структура урока:

1. Организационный момент.

а) побуждение,

б) вызов

2. Мотивация урока.
3. Актуализация опорных знаний. 
4. Определение темы урока, постановка целей и задач.
5. О знаке квадратного корня. Историческая справка.
6. Физкультминутка.
7. Применение квадратных корней. Решение задач..
8. Подведение итогов урока. Рефлексия.

Ход урока

Математика сложна-

Это знает каждый.

Только всем она нужна

Её знанье важно.

 

 

І.Організаційний етап

ПОБУЖДЕНИЕ

 

Метод: «Поздоровайся глазами» 

Цель – положительный настрой на работу, установление контакта между учениками.

 

Придумано кем-то просто и мудро

При встрече здороваться: ”Доброе утро!”

.           Ведь от улыбки всем станет теплей

            И поднимется настроение. 

Сейчас я с   вами поздороваюсь. Но поздороваюсь не словами, а молча - глазами. При этом постарайтесь глазами показать, какое у вас сегодня настроение

ІІ Перевірка домашнього завдання

Помічники перевіряють домашнє завдання на перерві і звітують про проведену роботу.

 

ІІ.  Вызов

Я хочу  начать  наш урок словами

"Приобретать знания - это храбрость.
Приумножать знания - это мудрость.
А умело их  применять - великое искусство"(слайд

Сегодня на уроке ,вы покажете свои умения по применению знаний 

 

Притча

 

Однажды  группа  оказалась в незнакомой стране перед высокой горой. Им надо было через нее перейти, но они понимали, что им нужен проводник. Проводник пришел, и перед тем, как начать путь, он сказал им: "Прежде всего, мы должны договориться с вами о взаимном уважении:. Я многие годы вожу людей, но каждый раз мы поднимаемся на разные горы. Я знаю, как ходить по горам, но именно эту гору я вижу впервые. Поэтому не теряйте бдительность, будьте   внимательны. Я могу только идти рядом с вами, но ноги за вас я передвигать не могу. Если вы не захотите подняться на эту гору    - это будет ваш выбор.

В дорогу 

Надеюсь, что сегодня на уроке вас ждёт и успех, и радость. И вы, работая в коллективе, покажете свою одарённость.

 

-Ребята, прочитайте пословицы, которые у нас прикреплены на доске. И каждый для себя выберете ту которая, вам понравилась больше всего.

 Отгадайте -загадку:

Он есть у  дерева, растении   и  в слове,

И в уравненьи тоже есть.

И стержневой, и мочковатый,

И кубический, и квадратный.

Надеемся, что каждый смог ответить: Это корень

 

 Улыбнитесь!

Вас снимает «Квадратный корень»

Итак, ключевое слово  сегодняшнего  урока КОРЕНЬ

1. Объявление темы и цели занятия. (Слайд)

Вы увидели, что слово "корень" встречается  не только на уроках математики.  

Давайте взглянем,  где же   вы еще  встречались с таким словом

1) подземная часть  растения ;(биология
2) общая часть  родственных слов (русский язык

3) уравнения (алгебра)

• А о каком корне  будет идти  речь      сегодня на уроке алгебры? (арифметическом  квадратном  корне).

• -Какую математическую задачу решает свинья, подрывая куст картофеля (извлекает корнеплод картофеля.

Сообщение темы урока

 

• И наш урок будет проходить под девизом:

«Покоряет вершины тот, кто к ним стремится».

 

• Что нужно знать , чтобы  успешно  извлекать квадратный корень

(необходимо знать свойства квадратных корней)

• Как вы думаете, чем мы будем заниматься сегодня на уроке? Попробуйте сформулировать цель нашего урока?

 

Есть в математике тема одна,

Арифметическим корнем называется она,

Корень появился, чтобы легче считать,

Двойка – показатель, это надо знать! 

 

• Итак, сегодня  на   уроке мы  отрабатываем свойства квадратных корней.

 

Актуализация опорных знаний

“Учение без размышления бесполезно,

но и размышление без учения опасно”

                       Конфуций

Что же мы уже знаем о квадратном корне??  Что нам сегодня пригодится на уроке. Давайте вспомним

Метод»Кластер

 

»

 

 

 

 

 

 

 

 

 

 

 

 

 

 

│

 

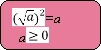
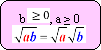
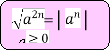
Интервью ( в кругу)    

1.Какие значения может принимать подкоренное выражение?

 2.Почему подкоренное выражение по определениюквадратного корня есть  число неотрицательное?                  

3.Как еще называется знак квадратного корня?

 

Составим карточку-справку «Свойства арифметического квадратного корня» из фрагментов формул левой и правой части и условий, при которых эти равенства верны. (слайд 6)

     =

   =                             a      

 = a_•

 

• А теперь посмотрите, пожалуйста, на экран и попробуйте  распределить  данные числовые выражения по  известным  признакам: . Прикрепите их на вашу карту

 

А         Д     

Р             И        З

П                   Н                         К  _•

По какому признаку вы  их распределили?. Проверим: (слайд )

 

АКК из произведения

АКК из дроби

АКК из степени

Прочитай слово

 

	5	88		7	2	3	10
П	Р	А	З	Д	Н	И	К

 

Получилось слово «праздник».

В каждой семье существуют свои традиции и обычаи, когда собирается вся семья и организует праздник. Самая лучшая семейная традиция это… отмечать день рождения как самый лучший праздник! 

Сегодня мы говорим об арифметическом квадратном корне и его свойствах. Оказывается и в семье АКК тоже отмечают Праздник арифметического квадратного корня.

• Когда же этот праздник?
•  Может быть, кто-то из вас знает?
• Чтобы ответить на этот вопрос, вспомните определение арифметического квадратного корня.

«Арифметическим квадратным корнем числа а, называется неотрицательное число, квадрат которого равен а».

 

На доске записана дата. Сегодня  31.01.19г . А существует дата, в которой будут выполнены все условия определения арифметического квадратного корня?

09.09.81  ,             01.01.01,   02.02.04,     03.03.09,     04.04.16.     А следующая?

День квадратного корня – праздник, отмечаемый девять раз в столетие: в день, когда и число, и порядковый номер месяца являются квадратными корнями из двух последних цифр года. Впервые этот праздник отмечался 9 сентября 1981года (09.09.81). Основателем этого праздника является школьный учитель Рон Гордон из города Редвуд Сити, Калифорния, США.  03.03.09  он  устроил соревнование, призом в котором послужила сумма 339$. А какой была  сумма приза в  2016 г?

 Давайте попробуем устроить внеочередной праздник квадратному корню и  покажем все, что мы знаем о  нем уже знаем и умеем

 

Миниатюра, которую разыгрывают ученики.

 

За столом сидит ученик, он в роли учителя математики. К столу прикреплен плакат «Экзамен по математике».

Вбегает ученик.

- Извлекать корни умеешь? – спрашивает экзаменатор.

Ученик:

- Да. Конечно. Нужно потянуть за стебель растения посильнее, и корень его извлечется из почвы.

- Нет, я имела в виду другой корень, например, из девяти.

- Это будет «девя», так как в слове «девять» суффиксом является «ть».

- Ты меня не совсем понял, я имела в виду корень квадратный.

- Квадратных корней не бывает. Они бывают мочковатые и стержневые.

- Арифметический квадратный корень из девяти?

- А, тогда три, так как три в квадрате равно девяти.

При этом ученик берет со стола плакат с записью  =3 и показывает его аудитории.

 

Мы с вами организуем сегодня праздник арифметического квадратного корня. На празднике принято дарить подарки. Давайте нашими подарками АКК будут верно выполненные задания.

 

Конкурс «Если бы я был учителем»

 

«Найди ошибку   (работа в парах  

 =8   (верно)                               =0     (верно)                                     =   ( ошибка)                                    = (ошибка)                             =20 (верно)

=900  (ошибка)                        = 8   (ошибка)                       =11а²   (верно)

 

 

Лесенка успеха   «До вершин математики»     

 

                                                                               Что больше: А или В

                                                                                     

 математики

                                                

                                              Укажите выражение,

                                                 имеющее смысл:

                                                                а) ; б) ;

                                                        в); г) ; д) .

                                                    вершин

                                    Найти a

                              

                                До

Тесты

 

Работа на ПК (индивидуальное задание)

"То, что я  слышу, я забываю;

 то что я вижу, я  помню;

то, что я делаю – я  понимаю".

 

Работа в группах

 

Ромашка Блума.

Заполняют Ромашку Блума.

Группа учащихся занималась  исследованием     способов  извлечения квадратного корня без калькулятора

МЕТОДЫ ИЗВЛЕЧЕНИЯ КВАДРАТНОГО КОРНЯ

(без использования калькулятора).

                                           Памятка ученику

 

Правильному применению методов можно научиться, только применяя их на разнообразных примерах.

Г. Цейтен

 

АРИФМЕТИЧЕСКИЙ СПОСОБ

То есть, узнать целую часть квадратного корня числа можно, вычитая из него все нечётные числа по порядку, пока остаток не станет меньше следующего вычитаемого числа или равен нулю, и посчитать количество выполненных действий. Неудобный, потому что громоздкий

Вычислить

• 9 − 1 = 8; 8 − 3 = 5; 5 − 5 = 0.

2. Выполнено 3 действия, зн. =3

Вавилонский способ

 

Древние вавилоняне пользовались следующим способом нахождения приближенного значения квадратного корня их числа х. Число х они представляли в виде суммы а²+b, где а²ближайший к числу х точный квадрат натурального числа а (а²?х), и пользовались формулой . (1)

Извлечем с помощью формулы (1) корень квадратный, например из числа 28:

Результат извлечения корня из 28 с помощью МК 5,2915026.

Как видим способ вавилонян дает хорошее приближение к точному значению

 

Разложение на простые множители

  

 

Пока у доски работают учащиеся, класс слушает историю  появления радикала

Учитель: Интересные факты о квадратном корне. Слово учащимся.

 

Растут ли в огороде радикалы?

Немного истории

Ребята,   вы уже  знаете как называется    знак корня  .А   сейчас послушаем , растут ли в огороде радикалы. Об этом нам поведают  работники   музея «Радикал».

 

• Находить значение квадратного корня умели вавилонские ученые еще четыре тысячи лет назад. Слово «корень» пришло в математику от арабов  Они представляли себе квадрат числа вырастающим из корня – как растение, – и поэтому называли корнями такие числа.
• В эпоху Возрождения европейские математики обозначали корень латинским словом Radix ( лат. -корень), а затем сокращённо буквой R. radicalis – коренной. Его следы можно найти   в словах: редис, редька  (отсюда произошёл термин «радикал».
• Начиная с 13 века итальянские и другие европейские математики обозначали корень   сокращенно Rх.
•  В 15 веке писали R212 вместо
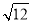
• . В 1525 г. появилось обозначение галочки  V для квадратного корня, которое вскоре вытеснило знак Rх, при этом над подкоренным выражением ставилась горизонтальная черта.
•  Современное обозначение корня впервые появилось в книге Рене Декарта “Геометрия”, изданной в 1637 году, где он  соединил горизонтальную черту с радикалом.

•  Современная запись корня появилась в книге «Руководство алгебры» французского математика Мишеля Ролля (1652-1719).

Есть хорошее высказывание одного из математиков: «Теория без практики мертва или бесплодна, практика без теории невозможна или пагубна. Для теории нужны знания, для практики, сверх того, и умение». Эти слова отражают сущность  применения квадратного корня..для решения практических задач.

 

Исследование применения квадратного  корня

 

В ходе сегодняшнего урока мы с вами вспомнили о родовых корнях, о семейных традициях. Интересно, а в каждой семье существует традиция активного зимнего отдыха:. А кто может нам сказать, какое спортивное событие  состоялось   в феврале  2014 года?

Да, это  XXII  зимние Олимпийские игры  2014 года, которые проходили в Сочи   с 7 по 23 февраля и в которых  Украина  принимала участие.  

Задача

1.Знаете ли вы, что на фасадном  куполе ледового дворца в Сочи был  размещен телевизор, площадь которого равна 25600 м² (12 хоккейных полей). Вычислите  длину стороны  этого телевизора, представив его в виде квадрата. .

 

Решение

S=;  a= ;  a= =160м

Задача.

2.Санно-бобслейная трасса в Сочи–1814 м (самая большая в мире по протяжённости) Сколько по времени займёт спуск с данной трассы, если боб достигает ускорение 1,5 

Решение

Уравнение движения     S=.

t=

t=   = =

 

3. .Кирпич падает с высоты 9 м. С какой скоростью он упадет на Землю? Решение:

 

Справка: Скорость свободного падения тела связана с высотой падения формулой , где g – ускорение свободного падения 9,81 м/с² .

Отсюда выразим v: .         H=9м, v=6   м/с

Решение данной задачи позволяет  узнать, насколько опасно ходить под карнизами домов.

 

4.Квадратные корни применяются при  многих расчетах. 
Так, например, в физике при определении первой космической скорости (10 класс)

 

 G-гравитационная постоянная:
M-масса Земли; 
R-радиус Земли.


Применение понятия квадратного корня в геометрии
                  
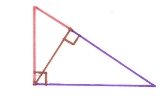
Это метрические соотношения в прямоугольном треугольнике

В геометрии часто встречаются средние значения, например катет прямоугольного треугольника равен среднему геометрическому гипотенузы и проекции этого катета на гипотенузу. А высота прямоугольного треугольника, проведенная к гипотенузе, есть среднее геометрическое проекций катета на гипотенузу.

 

5.Также площадь треугольника можно вычислить по формуле Герона: 

 

 

6) Площадь круга равна 314см² . Найдите радиус круга.

(S_кр =;).

Ответ: 10 см.

 

Помни!

На компьютере рекомендуется работать не более минут, а потом необходима зарядка для глаз, по сотовым телефонам нужно разговаривать не более  секунд, смотреть телевизор не более часов

 Задача

Заботящийся о своём здоровье ученик должен правильно питаться.

В день можно съедать не более  кг сладостей, дневная норма потребления хлеба составляет  кг, сливочного масла  кг. Сколько граммов сладостей, хлеба, сливочного масла может съедать в день ученик?

 

 

Физкультминутка ( под музыку)

Математическое лото.  (Работа в группах)

 

	= 25	=8	=3
	∙

 

На парту – один набор лото и варианты ответов, ответов больше чем заданий. Пока ребята выполняют задание, я готовлю для проверки лото на доске. Из предложенных вариантов дети выбирают карточку с верным ответом и прикрепляют её с помощью  стекеров. Заполняют соответственно 1-й ряд – I столбик, 2-й ряд – II столбик, 3-й ряд – III столбик. Таким образом, выполняется взаимопроверка.

 

Подведение итогов урока

 Закончим  урок  составлением  синквейна , ключевым словом  которого  есть корень.

Корень.

Арифметический квадратный.

 Складываем,  умножаем, делим.

Арифметический квадратный корень – число  неотрицательное.

Радикал.

 

корень;

  арифметический; квадратный

  извлекать, применять, использовать;

  помогут решать задания  ЗНО;

   важно!

Корень.

Квадратный, арифметический.

Завораживает, удивляет, вдохновляет.
Он открыл для меня красоту математики.

Победа!

 

Корень

Извлекали, возводили в степень, обобщали.

Было интересно.

Я молодец.

 

№ синквейн

Корень.

Квадратный, арифметический.

Решаем, думаем, находим.

Выдержим всё и добьёмся всего.

Эврика!

Я тоже вам сочинила синквейн.

Урок

Интересный, полезный

Информирует, учит, развивает

Сколько голов, столько и умов

Алгебра!

Рефлексия.

Урок у нас заканчивается.

Описание упражнения: Участники встают в кружок, и учитель предлагает каждому мысленно положить на левую руку все, то с чем он пришел сегодня, свой багаж настроения, мыслей, знаний, опыта, а на правую руку – то, что получил на этом занятии нового. Затем, все одновременно сильно хлопают в ладоши и кричат – ДА! или СПАСИБО!

Сьогоднішній урок я хочу закінчити словами:
Ви до знань зробили нині крок,
У навчанні бажаю вам удачі.
Хай цікавим буде кожний ваш урок
І розв’язуються правильно задачі!
Рік за роком йти вам слід
У наук чудовий світ.
А дорога ця і довга, і цікава,
Там чекають відкриття,
Що потрібні для життя.
Хай же успіх вам несе навчання справа

 

Д/З

1.Творческое:  мини-проект: Представьте, что  вы авторы сборника по  ЗНО. Вам нужно составить восемь заданий по теме: «Арифметический квадратный корень и его свойства».

2.Найти жизненные  задачи , в решении которых встречается кв. корень 

Любой урок, любая встреча
Всех вкладов на земле ценней,
Ведь каждый школьный миг отмечен
Неповторимостью своей.