Відрізок. Вимірювання відрізків

Тема. Відрізок. Вимірювання відрізків

Мета: 1. Домогтися засвоєння учнями змісту понять «відрізок», «внутрішня точка відрізка», «кінці відрізка», «перетин відрізків», «довжина відрізка» та змісту властивості вимірювання відрізків. 2. Виробити в учнів уміння роз­пізнавати на готовому рисунку відрізки і за описом ситуа­ції робити рисунки і пояснювати особливості розміщення точок із використанням вивчених понять, відповідно до умови задачі записувати властивість вимірювання відрізків і використовувати цей запис для розв'язування задач.

Тип уроку: формування знань, вироблення вмінь.

Обладнання: демонстраційне креслярське приладдя, табли­ця № 3 «Відрізки».

Хід уроку

I. Організаційний етап

Учитель перевіряє готовність учнів до уроку і повідомляє його тему.

II. Перевірка домашнього завдання

Правильність виконання домашнього завдання вчитель перевіряє, зібравши зошити учнів на перевірку.

III. Формулювання мети і завдань уроку. Мотивація навчальної діяльності учнів

Для успішного проведення цього етапу уроку вчитель про­понує учням розв'язати вправи на застосування властивості взаємного розміщення точок на прямій.

Запитання до учнів

1. Позначте на даній прямій а точку А. На які частини поділяє точка А пряму а?
2. Позначте на прямій а точки А і В. На скільки частин поділяють ці точки дану пряму а? Які з цих частин є променями? Чи є названі промені доповняльними? Чи є третя з утворених частин променем?

Виходячи з результатів виконання завдань, учитель фор­мулює, а потім узгоджує з учнями основну дидактичну мету уроку.

IV. Актуалізація опорних знань і вмінь учнів

Усні вправи

Чи правильні ці твердження? Відповідь поясніть.

1. Яка б не була пряма, існують точки, що належать цій прямій.
2. Через дві точки можна провести дві різні прямі.
3. З трьох точок одна лежить між двома іншими.
4. Існує тільки одна точка, що лежить між двома даними точками на даній прямій.

V. Формування знань учнів

План вивчення нового матеріалу

1. Уявлення про частини, на які будь-яка пряма поділяється двома своїми точками.
2. Означення відрізка з кінцями у двох даних точках. Елементи відрізка.
3. Вимірювання відрізків:

а) одиниці вимірювання, зміст поняття «вимірювання відрізків»;

б) довжина відрізка та її властивості;

в) зміст дії порівняння відрізків;

г) властивість вимірювання відрізків, які поділяються на дві частини деякою своєю точкою.

Методичний коментар

Навчальний матеріал уроку не є зовсім незнайомим для учнів, бо відповідає вже сформованим в учнів уявленням про відрізок як геометричну фігуру і про зміст операції вимірювання відрізків та порівняння двох відрізків за довжиною. Новими для учнів є поняття внутрішньої точки відрізка, поняття про перетин відрізків (як це викладено в підручнику) і поняття відстані між двома точками. Тому основне завдання вчителя полягає в тому, щоб викласти відомий матеріал з достатнім рівнем математичної строгості і довести до свідомості учнів новий матеріал з посиланням на набутий раніше досвід учнів.

Як і на попередньому уроці при роботі з теоретичним ма­теріалом максимально використовуємо наочність (таблиця № 3 «Відрізки»).

Таблиця № 3

VI. Первинне закріплення матеріалу

Усні вправи

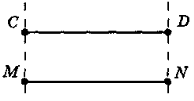
1. За рис. 8, 9:

а) опишіть взаємне розміщення точок;

б) скільки відрізків утворилось на рисунку? назвіть ці відрізки;

в) який з утворених відрізків найбільший? чому?

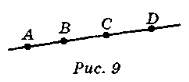
2. Користуючись рис. 10, розв'яжіть задачі:

1) Дано: AB = CD. Доведіть, що AC = BD .

2) Дано: AC = BD. Доведіть, що AB = CD.

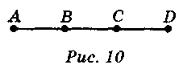
Письмові вправи

1. На розвиток просторової уяви: № 38, 39, 43.
2. На закріплення термінології: № 35, 41.
3. На вироблення первинних умінь використовувати влас­тивості вимірювання відрізків: № 44 (а, б), 2, с. 16 «Розв'язуємо разом».

Методичний коментар

При виконанні вправ, запланованих учителем на урок, учні мають:

а) використовувати термінологію і складати ланцюжки аргументованих міркувань (наприклад, точка X лежить між точками А і В, тому точка X належить відрізку АВ, а значить поділяє його на два відрізки, причому             АВ = АХ + ВХ);

б) при розв'язуванні задач на обчислення довжин відрізків обов'язково спочатку описувати ситуацію рівністю, використовуючи відповідну властивість вимірювання відрізків.

VII. Підсумки уроку

Усні вправи

1. Чи правда, що на рис. 11,а АС = ВС+АВ? чому?
2. Відомо, що MN = MK + KN . Який із випадків на рис. 12, б—г відповідає цій умові?

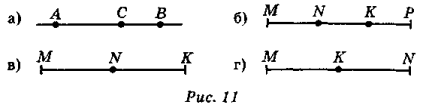
VIII. Домашнє завдання

1. § 2, с. 13, 14 — вивчити означення та властивості.
2. Письмово:

№ 40, 36, 45 (а, б), 55 (а).