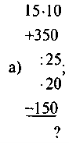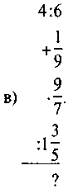Відсоткове відношення чисел

Тема.  Відсоткове відношення чисел

Мета: спираючись на вміння учнів знаходити відсоткове відношен­ня чисел, навчити знаходити вміст величини у відсотках і розв'язувати задачі, що передбачають ці дії.

Тип уроку: засвоєння знань, вмінь та навичок.

Хід уроку

І. Перевірка домашнього завдання

Вибірково перевіряємо зошити (у «слабких» учнів).

Правильні відповіді записуємо за дошкою, і один учень з місця
коротко коментує розв'язання.

Усні вправи

2. Виразіть у відсотках: 0,02; 0,08; 0,17; 0,56; 0,92.
3. Скільки відсотків становить: 3 м від 5 м; 40 см від їм; 32 г від 2 кг;

2,5 км від 12,5 км; грн від 3 грн?

4. Знайдіть: 1 %; 2 %; 3 %; 11 %; 20 %; 60 % від 15.

II. Засвоєння знань

Задача. У 6 класі навчається 30 учнів. На кінець І семестру математи­ку вивчали на достатньому рівні 12 учнів, а на кінець II семестру їх стало 18. На скільки відсотків виросла якість знань учнів?

Розв'язання

 Зрозуміло, що на попередньому уроці ми розв'язували схожу зада­чу, тому:

І спосіб

1) = 0,4 = 40% — на кінець І семестру;

2) = = 0,6 = 60% — на кінець II семестру;

3) 60 % – 40 % = 20 % — на стільки відсотків кращою стала якість знань у 6 класі.

Відповідь. 20 %.

 Дуже важливо зорієнтувати учнів на те, що цей спосіб не є найкра­щим, бо ми знаходимо зайві величини. Тому:

ІІ спосіб

1) 18 – 12 = 6 (учнів) — на стільки збільшилась кількість;

2) = = 0,2 = 20% — на стільки відсотків виросла якість знань.

Висновок

Щоб знайти, на скільки відсотків збільшилась або зменшилась вели­чина, треба:

а) дізнатися, на скільки одиниць збільшилось або зменшилось зна­чення величини;

б) обчислити, скільки відсотків становить ця зміна від початкового
значення.

III. Формування вмінь

Розв'язування вправ

І рівень (усні вправи)

Виразіть у відсотках зміну величини:

а) від 2 кг до 3 кг; б) від 2 кг до 4 кг; в) від 2 кг до 5 кг;

г) від 100 м до 96 м; д) від 100 м до 105 м; є) від 120 м до 200 м.

II рівень (письмові вправи)

1. Виразіть у відсотках зміну величини:

а) від 1 грн до 80 к.; б) від 25 ц до 3 т; в) від 4000 кгдо 5 т;

г) від 1 год до 30 хв.

2. Першого дня в магазині продали 250 кг капусти, а другого —230 кг. На
   скільки відсотків менше продали капусти другого дня, ніж першого?

а) Ціна товару 150 грн. Знайдіть ціну товару після двох послідовних
знижень, якщо перше було на 10%, а друге — на 5 %.

б) Ціну на товар, що коштував 150 грн, спочатку зменшили на 20 %,
а потім нову ціну збільшили на 20%. Знайдіть ціну товару після двох
переоцінок.

в) Ціну на товар, що коштував 100 грн, знизили на 20 %. На скільки
відсотків треба підняти нову ціну, щоб отримати початкову?

Розв'язання задачі 3(а)

1) 100 % – 10 % == 90 % — становить нова ціна від 150 грн;

2) 90 % = 0,9; 150 · 0,9 = 135 (грн) — нова ціна, після першої знижки;

3) 100 %  – 5 % = 95 % — друга нова ціна від попередньої;

4) 95 % = 0,95; 135 · 0,95 = 128,25 (грн) — нова, друга ціна.
Відповідь. 128,25 (грн).

Додатково

Ціну на товар знизили на 20 %, а потім підвищили на 20 %. Чи змінилась ціна товару порівняно з тим, якою вона була до зниження?

IV. Підсумок уроку

Логічні вправи

V. Домашнє завдання

1. Виразіть у відсотках зміну величини:

а) від 1 м до 1 м 80 см; б) від 2,5 кг до 2 кг; в) від 4 ц до 800 кг;

г) від 25 грн до 24 грн.

2. Ціну на товар, що коштував 150 грн., спочатку підвищили на 20 %,
   а потім нову ціну знизили на 20 %. Знайдіть ціну товару після двох переоцінок.
3. Повторення. Порівняйте значення виразу:

22,592 : 32 – 0,248 і 1,25 · 541 – 675,802.