ВИКОРИСТАННЯ ІННОВАЦІЙНИХ ТЕХНОЛОГІЙ НА УРОКАХ МАТЕМАТИКИ

 

 

ВИКОРИСТАННЯ  ІННОВАЦІЙНИХ  ТЕХНОЛОГІЙ

НА УРОКАХ МАТЕМАТИКИ

 

 

 

 

 

 

 

 

                                                       Вчитель   математики

 

                                              Мячкіна  Людмила Анатоліївна

 

ЗМІСТ

 

ВСТУП…………………………………………………………………………. 3

Розділ І   Розвиток компетентностей  учнів на основі інноваційних 

технологій……………………………………………………………………….4

Висновки до розділу І.

Розділ ІІ  Нетрадиційні  форми організації роботи на уроках 

математики……………………………………………………………………...9

2.1 Нестандартні уроки з математики ………………………………………16

Висновки до розділу ІІ……………………………………………………... . 46

Висновок……………………………………………………………………… 47

Список  використаної літератури……………………………………………48

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

ВСТУП

      Одним із пріоритетів стратегічного розвитку України визнано інтеграцію нашої держави у Європейське товариство.

      Сучасна школа сприяє розвиткові демократичної культури, формуванню необхідних для проживання у європейському співтоваристві компетентностей, політико-правових і соціально-економічних знань. Пріоритети загальноєвропейської освіти полягають у наданні молодому поколінню знань про спільну європейську спадщину та практичних умінь адаптуватися до життя й навчання в різних країнах Європи, бути мобільними, соціально здібними, здатними до комунікації та захисту своїх прав.

 Реформування освіти передбачає відновленню змісту навчання з орієнтацією на «ключові компетентності», оволодіння якими дозволить учням вирішити різні проблеми у професійному, соціальному, повсякденному житті.

 Педагогічний колектив постійно модернізує організацію навчально-виховного процесу, використовуючи сучасні досягнення науки і практики, упроваджує новітні технології навчання і виховання, що забезпечують створення організаційних, педагогічних, змістовних умов для здійснення освіти, їх самореалізації. Школа готує школярів до творчої роботи і виконує своє головне завдання – підготовку інтелектуальної, наукової, творчої еліти України.

До ключових компетентностей випускника школи відносимо:

      Пізнавальну компетентність

• Навчальні досягнення, уміння навчатися та оперувати знаннями.

Особистісну компетентність

• Розвиток індивідуальних здібностей і талантів.
• Обізнаність у власних сильних та слабких сторонах.

Самоосвітню компетентність

• Здатність до самонавчання.
• Гнучкість застосування знань, умінь, навичок в умовах швидких змін.
• Відповідальність  за рівень власної самоосвітньої діяльності.

Соціальну компетентність

• Співпраця, робота в команді, комунікативні звички.
• Здатність приймати власні рішення і прагнути до розуміння власних потреб і вимог.
• Ціннісні орієнтації.
• Культура міжособистісних відносин.

Здоров’я особистості

• Фізичне здоров’я.
• Психічне здоров’я.
• Рівень валеологічних знань.

                Випускник школи – це працелюбна особистість, готова до безперервної освіти, до свідомого вибору професії, уміє навчатися та оперувати знанням, має розвинену інтелектуальну, інформаційну, дослідну культуру (розвиток  пізнавальної особистісної компетентності випускника).

      Випускник школи – це особистість з високим рівнем освіченості і культури, здатна до творчої праці, професійного розвитку, співпраці, роботи в команді. Має комунікативні навички,  життєвий досвід  діяльності в групі, під керівництвом, самостійно, з літературою, з приладами, комп’ютером. (розвиток самоосвітньої та соціальної компетентностей випускника).

         Таким чином, модель випускника школи, покладена в основу навчально-виховного процесу школи, діє і дає бажані результати.

     Основною формою організації навчально-виховного процесу в сучасному загальноосвітньому навчальному закладі є класно-урочна система. Одиницею даної системи виступає урок.

     Урок – це більш або менш закінчений відрізок, або «клітинка», педагогічного процесу. В ньому, як сонце у краплині води, відображаються всі його боки. Якщо не вся, то значна частина педагогіки концентрується на уроці.

     Урок як форма організації навчального процесу у школі виник давно, але з того часу він постійно змінюється, набуває  нових форм та змісту.

     Як домогтися високої якості навчання на кожному уроці? Це питання хвилює сьогодні кожного вчителя. Відповідь: традиційні форми і методи потрібно використовувати разом з інноваційними підходами.

     Сучасний урок – це перш за все урок, на якому створено реальні умови для інтелектуального, соціального, морального становлення особистості учня, що дозволяє досягти високих результатів за визначеними метою та завданнями.

     При цьому суто інформаційне навчання треба поступово переводити в мотиваційне, коли на першому плані-свідома пізнавальна діяльність учнів, а вчитель, спостерігаючи, тільки допомагає дітям у кожній конкретній навчальній ситуації використовувати свої можливості і розвивати свої здібності, отримуючи впевненість у своїх діях. Тільки учень, який  чітко уявляє, що він хоче від учіння, буде свідомо навчатися і активно засвоювати зміст освіти.

     У даному посібнику подано матеріали щодо організації та проведення сучасного уроку за різноплановою нестандартною типологією уроків.

   Усе – це результат пошуків нових прийомів та узагальнення   практичного досвіду викладання  предмету.

 

 

 

 

 

 

 

 

 

 

 

РОЗВИТОК  КОМПЕТЕНТНСТЕЙ УЧНІВ  НА ОСНОВІ  ІННОВАЦІЙНИХ ТЕХНОЛОГІЙ

 

 

Наша мета полягає не в тому, щоб

зробити себе необхідними нашим дітям,

а навпаки, в тому, щоб допомогти їм

скоріше обходитись без нас.

К.О. Конраді

   Є жартівливий афоризм: «Освіта – це те, що залишається, коли все вивчене забуте». У  цьому жарті є велика частка правди. Дійсно, що може залишитися в голові людини, яка, намагаючись запам'ятати максимальну кількість фактичного матеріалу, забула його, відповідно до фізіологічних законів вищої нервової діяльності… і основних принципів організації освітянського процесу в нашій країні.

   Сьогодні освіта – це класно-урочна система, орієнтована в основному на засвоєння знань, формування умінь, навичок, а не на розвиток творчої особистості. Вона є педагогікою  авторитарних вимог, яка повністю  відповідала замовленню нашого суспільства 70-80-х років ХХ століття. Та за останні двадцять – тридцять років життя не просто змінилось, воно стало іншим. Постійне оновлення інформації та колосальні темпи її нагромадження зумовлюють потребу в таких членах суспільства, які здатні гнучко й оперативно адаптуватися до нових вимог, адекватно реагувати на нові заклики навчатися впродовж усього життя, розвиватися та творити. Але головне – змінилось соціальне замовлення школи: «Від людини, що знає, - до  людини, що вміє».

   В умовах реформи середньої освіти  особливого значення  набуває проблема вдосконалення технології навчання.

   Результатом традиційного  навчання є випускник, який уміє добре відтворювати  інформацію, але «розучився думати», не вміє знаходити самостійне  творче   рішення в складних ситуаціях. При традиційному навчанні спостерігається розрив між вимогами, що ставляться перед людиною в процесі навчання, і тими, які постають в реальному «дорослому житті».

  У даний час випускнику необхідні не тільки і не стільки знання, які постійно застарівають, а високий розвиток різних типів компетентностей: мовної (вміння читати, писати, спілкуватися за допомогою слова; логічної (здатності мислити абстрактно й логічно, аналізувати, чітко організовувати); просторово-візуальної (здатності мислити образами, відчувати цілісність, орієнтуватися в просторі); кінестетичної (здатності оперувати предметами, сприймати на дотик, вчитися через діяльність); соціальної (уміння контактувати з іншими людьми, співпрацювати, діяти в команді) і психологічної  (здатності усвідомлювати власне «Я», потреби і можливості, позитивно ставитися до себе, критично й творчо мислити, ухвалювати рішення, володіти собою, ставити цілі й досягати успіху).

     Розвиток компетентностей кожного учня неможливий без вживання інноваційних  освітніх і педагогічних технологій.

     Інновації можуть бути різними за масштабом, за потенціалом, можуть бути віднесені до різних складових учбово - виховного процесу, але, на мій погляд, вони завжди  повинні бути мотивовані і орієнтовані на конкретного вчителя, який працює  в конкретній школі з конкретними учнями. Ніякі інновації не повинні бути сліпо запозичені. Адже життя вносить свої корективи, і в результаті у будь-якого творчо працюючого вчителя складається своя технологія навчання й виховання, в основі якої можуть бути елементи різних педагогічних і освітніх технологій.

   Школа  ХХІ століття - школа компетентної, відповідальної людини, а значить – переходу  від знаннєвої до компетентнісної освіти. Це знайшло відображення у провідних освітянських документах – Державному стандарті базової і повної середньої освіти та Державного стандарту початкової загальної  освіти, Критеріях оцінювання навчальних досягнень учнів у системі загальної середньої освіти, Концепції профільного  навчання в старшій школі. Зокрема, в Концепції загальної середньої освіти зазначено: «Освіта ХХІ століття – це освіта для людини. Її стрижень – розвиваюча, культуротворча домінанта, виховання відповідальної особистості, яка здатна до самоосвіти і саморозвитку, вміє критично мислити, опрацьовувати різноманітну інформацію, використовувати набуті знання та вміння для творчого розв’язування проблем, прагне змінити на краще своє життя і життя своєї країни». Тому компетентнісний підхід  у навчанні є актуальною проблемою сьогодення.

   Механізмом формування компетентної  особистості на уроках математики є комплекс послідовних етапів: ціле покладання – визначення – очікуваних результатів – мотивація – ситуація успіху – здобування знань – формування умінь та навичок – творче використання знань, умінь, навичок у життєвих ситуаціях – контроль сформованості компетентностей – саморозвиток, самоосвіта особистості.

  Інноваційна значущість даного механізму  полягає у створенні ефективного процесу виховання інтелектуальної, самодостатньої, з потужним духовним потенціалом людини, здатної самостійно здійснювати життєвий вибір. Вважаємо, що змістовим та організаційним наповненням системи формування компетентностей учнів повинні бути такі методи та технології навчання, які в центр ставлять самостійну діяльність учня, розвивають критичне мислення та творчі здібності.

    Робота над формуванням компетентностей починається з визначення мети уроку (цілепокладання), що випливає із певної теми, і як наслідок – очікувані результати, тобто знання, уміння та навички, що їх учні опанують і застосують в конкретній ситуації. Важливим є вміння школярів самостійно визначати результати роботи на уроці. Для цього впроваджуємо прийом «Очікувані результати». Він дає змогу кожній дитині проаналізувати в кінці уроку, чи досягнув він поставленої мети, визначити над чим ще слід попрацювати.

   Велику увагу приділяємо  мотивації, яка фокусує увагу дітей на проблемі й викликає інтерес до теми уроку. На цьому  етапі ми намагаємося відшукати просту, зрозумілу, привабливу мету в колі вікових інтересів та захоплень дітей, адже, маючи особистісну зацікавленість, учень буде налаштований на ефективний процес пізнання та вдосконалення. Використовуємо також інтелектуальну розминку, відгадування загадок, асоціації та творчі завдання тощо.

    Головне – «підштовхнути» дітей до роздумів, самостійного пошуку відповідей і прийняття рішень. Лише за таких умов школярі будуть творцями уроку, а значить – і власного життя.

     У такому випадку вчитель виконує роль фасилітатора, організатора процесу навчання, в центрі якого – діяльність учня. Залученню школярів до процесу активного пізнання сприяють проблемні питання, які змушують розмірковувати не тільки над навчальним матеріалом, а й над загальнолюдськими цінностями, формують високодуховну особистість, її життєву компетентність. Сучасний урок не уявляємо без новітніх технологій, які сягають корінням у далекоглядні праці педагогів В.О. Сухомлинського. Вже зовсім звичайними на уроках стали прийоми інтерактивного навчання, у своїй практиці впроваджуємо роботу в групах парах. Групи використовують інформаційні, творчі, дослідницькі завдання. Такими видами робіт вчимо дітей співпраці  в команді, допомагаємо усвідомити власний внесок у спільну справу. Участь кожної дитини в роботі групи учні оцінюють спільно або індивідуально, що сприяє критичному ставленню до себе, відповідальності, вдосконаленню та соціалізації.

   Щоб заохотити до активності і почути думку кожного учня, впроваджуємо прийоми «Мікрофон», «Продовжи речення», «Мозковий штурм».

   Для формування компетентності учнів, розвитку їхніх творчих здібностей, навичок самостійного аналізу вивченого застосовуємо елементи технології критичного мислення.

   Одним із ефективних засобів залучення учнів до математики є гра.  Навчання  у грі покликане реалізувати, крім основної дидактичної мети, ще й комплекс цілей: вивільнення емоцій, можливість самовизначення, надихання і допомога розвитку творчої уяви, зростання навичок співробітництва, висловлювання власних думок.

   «Гра – шлях дітей до пізнання світу», - справедливо зазначав Максим Горький.

Метод проектів вважаємо основною технологією формування ключових життєвих компетентностей учнів.  Адже діти, працюючи над створенням проектів, навчаються критично мислити, чітко усвідомлювати, де і яким чином можна застосовувати набуті знання, генерувати нові ідеї, грамотно працювати з інформацією, бути комунікабельним, постійно самовдосконалюватися. У своїй практиці ми впроваджуємо дослідницькі, творчі, ігрові, інформаційні медіа – проекти. Учні створюють порт фоліо –систему своїх творчих наробок: малюнки, кросворди, казки тощо.

    Нашій роботі допомагають нестандартні форми  уроку, які стимулюють пізнавальну активність учнів, вміння діяти в незвичних ситуаціях, використовувати власний досвід, адаптацію до змін: урок засідання математичного клубу, урок-пошук істини, урок-дослідження, урок-представлення проектів.

  Формування компетентної особистості сприяє формуванню інтелектуально розвиненої, високодуховної людини та розвитку її творчих здібностей.

   Формування компетентної особистості повинно відбуватися не лише на уроках математики, а й під час вивчення інших предметів, у їх тісному взаємозв’язку.

  Ми впевнені, що зацікавити, повести за собою спроможний  лише той педагог, який сам перебуває у постійному пошуку. Адже ще В.О. Сухомлинський закликав: «Будьте самі шукачами, дослідниками. Якщо не буде вогника у вас, вам ніколи не запалити його в інших…»

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

ВИСНОВОК

 

    Чільне місце в системі нашої діяльності відведено урокам. Саме на них учні отримують важливі теоретичні знання з усіх предметів, вчаться їх практично застосовувати. Як відомо, істина повинна бути пережитою, а не викладеною і завченою. Тому сучасних  методик уроку рівно стільки, скільки компетентних  учителів. Бо кожен шукає свою, ту, що відповідає його інтелекту, темпераменту й досвіду. Ми намагаємось  будувати уроки таким чином, щоб учні закріплювали матеріал не шляхом простого заучування і переказування вивченого матеріалу, а шляхом розвитку  мислення, вирішення практичних завдань.

    Поєднуючи розвиток інтелектуальних здібностей учнів, дослідницьких умінь і творчого потенціалу дітей, ми формуємо активну, компетентну, творчу особистість.

   Таким чином, інноваційні технології навчання сприяють творчому засвоєнню знань. При цьому навчальний процес характеризується високою інтенсивністю, супроводжується   підвищеним інтересом, одержані знання відрізняються глибиною та міцністю.

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Нетрадиційні  форми організації роботи на уроках математики

 

 

Вчитися можна лише весело...

Щоб перетравити знання,

Потрібно поглинати їх з апетитом.

Ф. Франс

 

Сучасна освіта – це освіта для людини. Її стрижнем є розвиваюча, культуротворча домінанта, виховання здатності до самоосвіти і саморозвитку особистості, яка вміє використовувати набуті знання і вміння для творчого  розв'язання проблем, критично мислити, опрацьовувати різноманітну інформацію, прагне змінити на краще своє життя.

Роль учителя є вирішальною у процесах формування мислення, гартування характеру й виховання  моральних якостей учнів. Він генератор і джерело ідей, якими керується другий суб'єкт педагогічного процесу – учень. Від педагогічної майстерності вчителя залежить націлювання учнів на належний навчальний лад. Тоді цілі вчителя стають  і цілями учнів – у них одна мета. Природно, що прагнення обох до єдиної мети прискорює  її досягнення. Щоб керувати процесом формування і розвитку здібностей учнів, треба знати актуальні і потенціальні їх рівні. Водночас виникає проблема: якими повинні бути умови середовища, щоб кожен  школяр міг розвинути свої творчі нахили й перетворити їх у творчі досягнення.

Високий рівень успішності учнів не завжди поєднується з високим рівнем творчої обдарованості. У зв'язку з цим потрібно намагатися сприяти сприятливі умови для самовираження кожної дитини в різних видах діяльності, в тому числі й навчально-творчій.

Саме уроки математики  дають виключні можливості прищеплювати інтерес до  творчих  пошуків, виховувати в дітей бажання шукати нові, кращі шляхи виконання дорученої справи. Справді, пошук кращих способів розв'язання нестандартних задач, нестандартних розв'язань традиційних задач, аналіз змісту теорем, бесіди про видатних   учених, організація способу здобуття знань – усе це є важливими складовими на шляху розвитку творчих здібностей учнів. Дуже важливо, щоб діти повірили у власні  сили і здібності, зрозуміли, що без напруженої систематичної  праці прийти до успіху неможливо.

Працюючи в школі та спостерігаючи за школярами, ми дійшли висновку, що для багатьох учнів визначальним чинником вивчення математики є її загальновизнана роль у житті та інших науках. Але є учні, які на уроці перестають слухати або, навпаки, тільки роблять вигляд, що слухають, але не чують, якщо новий матеріал їх не зацікавив з самого початку. Запобігаючи байдужості на уроці, появу нового матеріалу потрібно підпорядкувати природній допитливості школяра: новий факт не виникає з „нічого”; разом з дітьми з'ясувати можливості його застосування, а форму організації навчання обирати оптимальною. Отже, завдання, яке постало перед учителем, -  збудити здібності  своїх учнів, виховати в них сміливість думки і впевненість у тому, що вони розв'яжуть  кожну задачу, в тому числі й творчого характеру, - без особистого захоплення справою, без наявності педагогічного такту і таланту, без умілого вибору форм навчання, методів, прийомів та засобів втілити в життя неможливо.

Особистісно зорієнтоване навчання передбачає навчальний процес, за якого як учні, так і вчителі почувають себе комфортно. Ми, як і, мабуть, кожний педагог, отримуємо задоволення від роботи, коли бачимо позитивні наслідки своєї праці, учні – також. Однією з причин, що допомагають отримати найкращі результати, є, на мою думку, вибір оптимальної форми навчання. Традиційні форми навчання математики іноді заважають здібному учню повністю проявити себе, тому один із шляхів подолання цього ми вбачаємо у використанні нетрадиційних форм організації навчання.

Основною формою організації навчальної діяльності є класно-урочна система навчання, за якої основною формою організації навчання є урок. У дидактиці під уроком розуміють основну одиницю освітнього процесу, чітко обмежену часовими рамками (45 хвилин), планом роботи та складом учнів (класом).  Під формою організації навчання розуміють взаємодію  вчителя й учня, яка регулюється визначеним, завчасно встановленим порядком і режимом. Організаційні форми значною мірою впливають на конкретний хід навчання  та загальний хід і результат навчального процесу. Все гострішою стає проблема вдосконалення форм організації процесу навчання, знаходження відповіді на запитання „Як навчати, як створити умови для розвитку та самореалізації особистості в процесі навчання?”.

Головною в роботі вчителя стала проблема зробити навчання цікавим: для учня це означає посильним і успішно-результативним, для вчителя – радісним.

Підтримання бажання вчитися вимагає зміни способів і форм сприйняття нового, створення різних ситуацій для застосування вивченого. Виховання ж інтересу передбачає реалізацію багатьох методичних прийомів, пошук і застосування різних технологій навчання, а головне – невтомну вчительську працю, самовдосконалення і самоосвіту.

Систему уроків намагаємося побудувати так, щоб учні працювали з повною віддачею сил, з інтересом. Школярам подобаються завдання творчого характеру, які розвивають у них пізнавальний інтерес: складання казок, кросвордів, ігор; виконання творчих робіт; участь у математичних змаганнях. Готуючись до уроків, учителі  дотримуються  таких правил:

•                  Урок має бути продуманим до дрібниць, щоб його етапи логічно випливали один з одного, а учні розуміли, чому, що і за чим вони роблять на занятті.
•                  Корисно діяти за принципом „Краще один раз побачити, ніж сто разів почути”. Усе, що вчитель говорить, бажано втілювати в зримі образи. Наочність має бути динамічною, щоб показати невидиме: хід міркувань, зв'язок між поняттями.
•                  Учнів потрібно ретельно готувати до усвідомлення теми уроку, а не записувати її наперед.
•                  На уроці повинно бути цікаво. Але без емоцій, без переживань розум не напружується. Зацікавленість виникає там, де вчителю вдається захопити дітей своєю емоційністю.

Велику увагу приділяємо розвитку уяви, нестандартного мислення і фантазії учнів. Тому уроки можуть бути грою, змаганням з появою казкових героїв. Залежно від теми, мети та класу, в якому проходить урок, проводимо уроки-лекції, уроки-практикуми, уроки систематизації та узагальнення знань у формі подорожей, конкурсів, математичних змагань. Адже, передусім, важливим є умови для створення творчої атмосфери, самокерування, взаємодопомоги і взаємоконтролю. Саме нестандартні уроки сприяють розвитку творчих здібностей дітей, виховують навички дослідницької діяльності, дають високий ефект практичної спрямованості матеріалу, що, зрештою, приводить глибокого розуміння предмета, зацікавленості  ним. Але само собою зрозуміло, що  розумову самодіяльність, тямущість  не можна  ні „втокмачити”, ні  „вкласти” в чиюсь голову. Практика показала , що результати  надійні лише  тоді, коли введення в деяку галузь знань відбувається в легкій, приємній і ненав'язливій формі, на цікавих і дотепних прикладах, в ігровій формі. Крім того, в такій формі навчання є більш захоплюючим, доступним. Як правило, ігрову форму уроку діти сприймають з найбільшим захопленням і працюють здружено та натхненно. Взагалі, така форма роботи є продуктивною і викликає в учнів значно більший інтерес та ентузіазм. Але яким би  за формою чи змістом  не був урок, головним у ньому є праця – організована, результативна, творча. Кожен такий урок є уроком, якого чекають, на якому учні відчувають радість творчої праці, де виховання досягається не штучно, не мимохідь, а послідовно і логічно через навчання. Урок вважаємо результативним, якщо учні глибоко усвідомили і „привласнили” мету вчителя, коли вона глибоко перетворилася в їхнє особисте прагнення, бо сучасний урок – це урок демократичний, глибоко продуманий, організований і керований, що проводиться не для учнів, а разом з ними, з урахуванням дитячих можливостей, потреб та інтересів. Одним словом, на уроці не може бути об'єктів і суб'єктів. Лише суб'єкти – по обидва боки вчительського столу. Таким чином, дитину спочатку потрібно навчити хотіти й любити, а вже потім – знати і вміти.

 Ігри, які ми використовуємо на уроках математики, розвивають мислення, кмітливість, збагачують увагу учнів, спонукають їх до пошуку, активізують клас під час вивчення нового матеріалу і закріплення вже вивченого матеріалу. Гра – творчість, гра – праця. У процесі гри в дітей виробляється звичка зосереджуватися, мислити самостійно, розвивається потяг до знань. Захопившись, учні не помічають, що вчаться, - пізнають, запам'ятовують нове, орієнтуються в незвичних ситуаціях, поповнюють запас уяв, понять, розвивають фантазію, зорову пам'ять. Навіть найпасивніші з учнів включаються в гру з великим бажанням, докладаючи зусилля, щоб не підвести товаришів по грі. Процес гри, її результати часто спонукають деяких учнів замислитися, які прогалини є в їхніх знаннях та як їх ліквідувати.

Поєднання всіх елементів гри та їх взаємодія підвищують організованість, ефективність гри, приводять до бажаних результатів.

У багатьох іграх в основу покладено принцип змагання, який підсилює емоційний характер заходу. Кращі результати гра приносить, коли змагання відбувається між командами, а мотив змагання виражається  в назві гри. Наприклад: „Математичний футбол”, „Брейн-ринг”, „КВК” та інші.

Ігрові форми  уроків широко використовувати як засіб навчання, виховання і розвитку. Гра вчить бути витриманим і у важкі хвилини боротися до кінця.

Одним із видів нетрадиційного уроку є урок-казка. Такий урок проводимо, використовуючи казкових персонажів, героїв мультфільмів, кінофільмів. Але казку можна написати і вибрати казкових героїв самим, спираючись на той матеріал, що вивчається у класі.

Уроки-казки супроводжуються кольоровими ілюстраціями, різнобарвними картинками, які викликають в учнів естетичні емоції, відчуття краси математики. Казки та ілюстрації до них інколи виготовляють самі учні. Іноді як домашні завдання на вихідні або на канікули пропонуємо написати математичну  казку школярам, бо казка допомагає формувати уяву. Крім того, на уроках, на яких знаходиться час для казки, завжди панує гарний настрій, а це – запорука продуктивної праці.

Казки часто допомагають зрозуміти, чим живе учень, про що мріє. Створюючи казку, діти творчо підходять до завдання, вигадують, виявляють літературні здібності. Сама казка – це незвичне явище на уроках математики, а все незвичне робить дітей сміливішими.

Інший вид організації навчання, які ми  впроваджуємо у свою діяльність, є уроки – подорожі. Вони задовольняють  інтереси підлітків, чиї ідеали пов'язані з романтизмом, фантазією, витівкою. Така форма проведення уроку несе значне пізнавальне навантаження і служить вдалим підсумком вивчення будь-якої теми чи серії тем. Виконуючи досить серйозні функції, урок-подорож ніколи не втомлює дітей і дає їм позитивний емоційний заряд. Він стимулює творчу діяльність учнів, сприяє мобілізації їхніх здібностей. Саме цей емоційний стан окрилює учнів. Найчастіше уроки – подорожі невіддільні від казкових героїв чи за сюжетом нагадують казку. Подорожі здійснюються до вигаданих країн за вигаданими маршрутами.

Нестандартною формою організації проведення уроку є впровадження лабораторно-практичних робіт. Характерними особливостями таких робіт є:

•      використання креслярських інструментів, моделей, шаблонів, обчислювальних приладів;
•      обчислювальна обробка результатів вимірювань з допомогою необхідних формул, порівняння результатів вимірювань і обчислень.

Лабораторно-практичні роботи мають значне освітнє та виховне значення. Вони дають можливість більш повно і свідомо з'ясувати математичні залежності між величинами, навчитися вимірювати та обчислювати значення із заданим ступенем точності; сприяють удосконаленню навичок наближених обчислень, роботі з математичними таблицями та  обчислювальними приладами. Вони вносять різноманітність у навчальний процес, сприяють активності та самостійності учнів, підвищують якість їх знань з математики.

Підвищення ефективності навчального процесу, досягнення високого інтелектуального розвитку учнів, забезпечення оволодіння  ними навичками саморозвитку особисто значною мірою можна домогтися, використовуючи сучасні інноваційні технології, зокрема технології інтерактивного навчання, перетворюючи таким чином традиційний урок в інтерактивний.

Особливістю інтерактивного навчання є підготовка молодої людини до життя і громадянської активності в громадянському суспільстві та демократичній правовій державі на заняттях з будь-якого предмета. Це вимагає активізації навчальних можливостей учня замість переказування абстрактної, „готової” інформації, відірваної від їхнього життя і суспільного досвіду. Такі уроки дають учням основні пізнавальні та громадянські вміння, а ще навички і зразки поведінки.

Вони захоплюють учнів, пробуджують учнівський інтерес, навчають самостійного мислення та дій. Ефективність і сила впливу на емоції та свідомість вихованців значною мірою залежить від умінь і стилю роботи вчителя.

Застосування інтерактивних технологій висуває певні вимоги до структури уроків. Як правило, структура таких занять  складається з п'яти елементів:

•   мотивація;
•   оголошення, представлення теми та очікуваних навчальних результатів;
•   надання необхідної інформації;
•   інтерактивна вправа – центральна частина заняття;
•   підбиття підсумків, оцінювання результатів уроку.

 Використовуючи нетрадиційні форми і методи навчання дає можливість зробити процес навчання цікавим та всепоглинаючим, створити у дітей робочий настрій; допомогти подолати труднощі в засвоєнні навчального матеріалу.

Наводимо декілька прикладів проведення уроків у нашій школі.

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Узагальнення — це, напевно, най­легший і найімовірніший шлях роз­ширення математичних знань.

В. Сойєр

Мета: узагальнити й систематизу­вати знання, вміння і навички учнів; розвивати пізнавальну ак­тивність, логічне мислення, ува­гу; виховувати культуру матема­тичного мовлення, упевненість у своїх силах.

Обладнання: картки з індивіду­альними завданнями, таблиці.

ХІД УРОКУ

І. Мотивація навчальної діяльності

Сьогодні ми підіб'ємо підсумки вивчення теми «Застосування різних способів розкладання мно­гочленів на множники». Я сподіваюсь на успішну працю, що на уроці ви зможете показати свої знання, вміння, кмітливість. Тож будьте уважними, думайте, запитуйте, пропонуйте, оскільки нам разом з вами йти шляхом до істини.

Урок ми проводимо у формі діло­вої гри, що має назву «Компе­тентність». Що ж це означає?

Компетенція — це готовність за­стосувати знання, вміння та на­вички для фахового розв'язання проблеми. Отже, це готовність учня використати набуті знання, навчальні вміння і навички, а та­кож способи діяльності в житті для виконання практичних та теоретичних завдань.

Компетентний (лат. — належний, відповідний) — це той, хто во­лодіє необхідною інформацією і вміє застосовувати набуті знан­ня і досвід.

Отже, наскільки ви компетентні в розкладанні многочленів на множники, покаже сьогоднішній урок.

Клас розподілено на три коман­ди — зі своїми капітанами і гру­пою «експертів», які допоможуть мені фіксувати ваші успіхи. Капі­тани команд під час гри будуть прикрашати «дерево компетент­ності», а експерти — заповнювати жетонами скарбничку. У кінці уроку підбиваємо підсумок.

Перед початком гри необхідно повторити теоретичний матеріал. Для цього капітан пе­ревіряє правила в кожного  члена команди.

Перший тур    

       Конкурс-розминка «Мозковий штурм»  (усне розв'язування задач кожною командою)

1.       Укажіть за допомогою сигналь­них карток номер правильної відповіді. Якщо правильної від­повіді немає, то назвіть її.

 

Завдання:                                                            Відповіді:

1.                   3а²-3в²=                                                          1.  (2а+в)²
2.                   а²+4ав+4в²=                                                   2.  (а-2в)²
3.                   –а²+2ав-в²=                                                    3.  3(а-в)(а+в)
4.                   3а²-6ав+3в²=                                                 4.  3(а-в)²
5.                   а³+8в³=                                                        5.  (а+2в)(а²-2ав+4в²)

2. Закінчіть вирази:

1.    -18х + 9  =  ...  (2х - 1);
2.    6ах  + 9а - 3а ² = ... (2х +3 - а);
3.    а²-х² =   . . .;

4.    9 - 25у²  = . . . ;
5.    64 + 16у + у ² = ...

3. Обчисліть:

1. 67²  - 33²  =  ...;
2. 75²  + 2∙ 75∙ 25 + 25²;

            4. Знайдіть суму коренів рівнян­ня   х² – х = 0.

5. Заповніть порожні клітинки:

           а)   □² - у² = (а - □)(а + □);

               б)  (х  +□)² =□ ² + 2□у + у².

Другий тур

Конкурс  «Дивить  не   помились» (учні отримують диференційовані  завдання.)

Рівень А

Виконайте за зразком:

1. а²  -  в²  = (а + в)(а - в) ;
2. т²-п² =______ ;

3.2²-х² =______;

4.                    (а + в) ²  =  а ²  + 2ав + в²  ;
5.                    (т + п)²  =  _  _  _  _  _  _    ;
6.                    (2 + х)²  =  _  _  _  _  _  _   ;
7.                    25 – т²  =  _  _  _  _  _  _  ;

Рівень Б

1.   Обчисліть: 56 ²  - 44²  =

2. Спростіть: (х - 7)² - х²  =
3. а² - □² =(□ + 9)(□ - 9).

Рівень В

1. Доведіть, що вираз (7n - 1)²-36  ділиться на 7.
2. Заповніть порожні клітинки:   □ - □  + с(а - в) = (а - в)(1+□).

Третій тур

Конкурс «Знайди помилку» (завдання для кожної команди)

1. (х - 7) ² =  х ² - 14х  + 40.
2. (х - 7)²  = х² - 7².
3. (х - 7)² = х² - 7х + 49.

Четвертий тур

Конкурс капітанів

1. Доведіть, що при будь-яких зна­ченнях n вираз (n-4)² - n²  ділиться на 8.

2. Розв'яжіть рівняння:   --х ² -- ( х + 5 )( х – 5) = х

З . Скоротіть:   

П'ятий тур

Естафета «П'ять кроків до успіху». Хто швидше?

(Робота в групах. Ключове слово «УСПІХ». Учні працюють на місцях — розв'язують тести.)

1. (8а+b)(8а-b)=  ;               У :  64а² – в²
2. 25х² – 16  = ;                                             С :  (5х – 4)(5х + 4) 

3. 65²  + 2 ∙ 65 ∙ 35 + 35²  = ;                                       П :  10000
4. 7,49 ∙ 2,5 + 2,5 ∙ 2,51 = ;                                           І :  25
5. (х^п-2)( х^п-2) = ;                                Х : (х^п -2)²

Шостий тур

Конкурс  «Цікавинки  навчання»

1. Відгадайте кросворд. ( Уч­ні  працюють  у   групах.)

По горизонталі

1. Рівність, що має змінну. (Рів­няння)
2. Учений, який відділив алгебру від математики й розглянув її як самостійний предмет. (Аль-Хорезмі)
3. Один зі способів розкладання многочленів    на    множники. (Групування)
4. Множник, який можна вине­сти за дужки. (Спільний)
5. Многочлен, що має два додан­ки. (Двочлен)
6. Наука, що вивчає розкладання многочленів    на    множники. (Алгебра)
7. Число,   що  задовольняє  рів­няння. (Корінь)

По вертикалі

8. Сума кількох одночленів. (Мно­гочлен)

 

11																88
22
										О
										33
										О
			44
			55
			66
	77

Сьомий тур  

Підбиття підсумків

Наш урок завершується. Згадай­те, які слова частіше зустрічались на уроці: «знаю» чи «вмію»?

Спробуйте дати оцінку своєму емоційному настрою на уроці. Наскільки вам було комфортно? Нехай допоможуть вам дати відповідь ці емблеми: «радість ус­піху», «набув певну суму знань», «не задоволений собою на окре­мих етапах уроку».

(Емблеми прикрашають дерево ком­петентності. Капітани команд визна­чають найактивніших учнів.)

Домашнє завдання.

Повторити тему. Виконати само­стійну роботу з підручника, скласти кросворд.

Учитель. На початку уроку клас було розподілено на три команди конкурентів. Але наш урок під­тверджує протилежну думку, ви — клас однодумців, які вміють засто­совувати набуті знання, а це озна­чає, що кожний із вас ,як сьо­годні, так і в майбутньому, буде компетентним у певній галузі. Спасибі за співпрацю на уроці.

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Тема:  Декартові координати та вектори на 

            площині

 

Мета: Систематизувати практичні навички 

            застосування вивченого матеріалу до 

            розв'язування  задач і вправ з даної 

            теми; розвивати інтерес до математики;   

            вчити етиці та культурі спілкування.

Обладнання:  кодоскоп.

 

Організація  класу до уроку.  Учнів класу попереджено про урок „Брейн - ринг, його тему, правила гри, умови оцінювання, а також розділено їх на  команди, обрано членів журі та спостерігачів.

 

Правила гри. Зачитується запитання чи умова задачі. Першою має право відповідати та команда, чий прапорець першим піднявся над столом.  Це визначають спостерігачі.

 

Умови оцінювання. Кожна правильна та чітка відповідь на запитання І туру оцінюється у 3 бали, а правильно розв'язана задача ІІ туру – у 5 балів. Неточна або неповна відповідь зменшує кількість балів. Різницю одержує команда, яка доповнила або уточнила відповідь.

 

Організація класу на уроці. Кожна команда сидить за окремим столом. Капітани команд мають по одному прапорцю.

 

ХІД УРОКУ

 

Повідомляється тема та мета уроку. Нагадуються правила гри та умови оцінювання.

 

І тур (актуалізація опорних знань)

 

1.   Як позначаються координати точки?
2.   Які знаки мають координати точки, якщо вона належить І, ІІ, ІІІ, ІУ четверті?
3.   Чому дорівнюють абсциси точок, що лежать на осі ординат?
4.   Чому дорівнюють ординати точок, що лежать на осі абсцис?
5.   Які координати початку координат?
6.   Яка формула  координат середини відрізка?
7.   Яка формула відстані між точками?
8.   Назвіть загальне рівняння прямої?
9.   Яке рівняння кола?
10. Що таке вектор? Як позначають  вектор?
11. Які вектори називаються однаково напрямленими?
12. Які вектори називають протилежно напрямленими?
13. Що таке нульовий вектор?
14. Які вектори називаються рівними?
15. Що таке координати вектора?
16. Як обчислюється абсолютна величина вектора, заданого координатами?
17. Дати означення суми векторів.
18. Сформулювати правило  „трикутника” додавання векторів.
19. Сформулювати правило „паралелограма ” додавання векторів.
20. Дати означення різниці векторів.
21. Дати означення множення вектора на число.
22. Які вектори називаються колінеарними?
23. Дати означення скалярного добутку векторів.
24. Як позначається кут між векторами?
25. Чому дорівнює кут між однаково напрямленими векторами?
26. Яка необхідна і достатня ознака колінеарності векторів?
27. Яка ознака перпендикулярності векторів?

 

ІІ тур (узагальнення і систематизація знань)

 

Деякі умови задач проектується на екран за допомогою кодоскопа.

 

1.Доведіть, що чотирикутник АВСД  з вершинами А (1;2), В (2;1), С (-1;-2),

Д (-2;-1) є прямокутником.

2.Вершинами трикутника  точки А (0;4),

В (-2;-1), С (4;0). Обчисліть довжину медіани, яку проведено до сторони АС.

3.Дано точки А (0;1), В (1;0), С (1;2),

Д (2;1). Доведіть рівність векторів АВ і СД.

4. Дано вектори (2; -1), (-1;2). Знайдіть

=+

5. Вершинами  трикутника є точки

А(1;1), В(1;4), С(3;2).Складіть рівняння медіани до сторони ВС.

6. Дано вектори (-1;2) і (3;-2). Знайдіть

= +.

7. Дано вектори (-1;1) і (2;-1). Знайдіть

= 2-.

8. Дано вектори (1;-1) і (2; -1). Знайдіть  таке число т, щоб вектор +т був перпендикулярним до вектора 

9. Знайдіть кут між векторами  (4;3) і (3;4).

10. Дано вектори (3;2) і (0;-1). Знайти вектор = -2+4 та його абсолютну величину.

11. Знайдіть значення х, при якому вектори (1;-1),(х;2) колінеарні.

12. Знайдіть скалярний добуток векторів і , якщо ׀׀ = 3,  ׀׀ = 8,     φ =120ْ , де φ-кут між векторами і .

13.Знайдіть скалярний добуток векторів (0;2) і (3;0).

Оцінювання. Журі визначає команду-переможця, а вчитель виставляє оцінки учням із врахуванням кількості балів, набраних кожною командою у грі, і особистого внеску кожного учня.

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

з використанням інтерактивних технологій

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

ТЕМА. РІВНЯННЯ. ЗАГАЛЬНІ ВІДОМОСТІ ПРО РІВНЯННЯ.

 

Мета: освітня: активізувати загальні відомості учнів про рівняння, корені рівняння, вміння розв'язувати нескладні рівняння на основі залежності між компонентами арифметичних дій; формувати навички розв'язувати задачі за допомогою складання рівнянь; розвиваюча: розвивати вміння лаконічно й математично грамотно висловлювати свою думку; виховна: виховувати працьовитість, спостережливість, киітлмвість.

 

Тип уроку: засвоєння нових знань.

 

Обладнання:  таблиця-ключ, правила проведення інтерактивних вправ «Мікрофон» та «Незакінчені речення»

(пам'ятка).

 

Епіграф уроку:

 

Не достатньо мати лише добрий розум,

головне -  це раціонально застосовувати його.

                                               Р.Декарт

 

ХІД УРОКУ

І.Організація классу

 

ІІ.Мотивація пізнавальної діяльності

 

1.Історична довідка про рівняння

 

Починаючи з першого і по шостий клас ви вивчали математику . А тепер , коли ви стали семикласниками, вам видавали аж два підручники замість одного – це «Алгебра» та «Геометрія». Сьогодні у нас урок алгебри. Що ж це за незнайоме слово? Ми починаємо вивчати алгебру з розділу «Рівняння». І це недаремно, тому що алгебра почалася і довго розвивалася саме як наука про рівняння. Навіть сама назва  «алгебра» утворилася від слова «аль-джебр», яке відомий узбецький математик ІХ ст. Мухаммед Аль-Хорезмі використовував у своїй книзі про розв'язування рівнянь.

   Перші рівняння люди вміли розв'язувати дуже давно. Єгипетські вчені майже 4 тис. років тому невідоме число в рівнянні називали «хау» (у перекладі  «купа») і позначали спеціальним знаком. У папірусі, що дійшов до нас, є така задача:

    Купа і її сьома частина  становить 19.

    Знайдіть купу.

    Сьогодні ця задача виглядала б так: «Сума невідомого числа і його сьома частина дорівнює 19. Знайдіть невідоме число». Щоб розв'язати цю задачу, необхідно скласти рівняння:

                   Х + Х=19.

2.Повідомлення теми і мети уроку

- Відповідно до мети уроку кожний із вас повинен поставити власні цілі, над досягненням яких і буде працювати на сьогоднішньому уроці. Подумайте, які це будуть цілі, й обговоріть їх у парах.

ІІІ.Актуалізація опорних знань

Отже, ви зрозуміли, як важливо уміти розв'язувати рівняння. Давайте пригадаємо прості правила, які ви вивчали ще в молодших класах і за якими ми можемо знайти невідомий компонент рівняння.

Технологія «Мікрофон»

   Учитель ставить запитання до учнів. Учням запропоновано певний предмет (ручка, олівець), що виконуватиме роль мікрофона. Діти передають його один одному, по черзі беручи слово. Відповідає тільки той, у кого уявний мікрофон.

•          Як знайти невідомий доданок?
•          Як знайти невідоме зменшуване?
•          Як знайти невідомий від'ємник?
•          Як знайти невідомий множник ?
•          Як знайти невідоме ділене ?
•          Як знайти невідомий дільник ?
•          Знайдіть невідомий член рівняння 5х = 50,

х – 7 = 42, 18 – х = 75.

ІУ.Вивчення нового матеріалу. Сприймання й усвідомлення загальних відомостей про рівняння

Пояснення вчителя. Ви всі любите розв'язувати кросворди. Рівняння можна теж уявити як кросворд, де в порожню клітинку потрібно поставити деяке число. Наприклад, 3* - 27 = 9, але ніхто не рисує порожню клітинку, а на її місце ставить букву, що називається змінною. Змінні найчастіше позначаються буквами  Х та У, але не можна позначати змінну будь-якою буквою.

 

РІВНЯННЯ – це рівність, що містить змінну.

 

Якщо в рівнянні 3х – 27 = 9 замість  змінної х написати  число 12, то дістанемо правильну числову рівність 3 12  - 27 = 9. Кажуть, що число 12 задовольняє дане рівняння.

 

Число, яке задовольняє рівняння, називається коренем  рівняння або розв'язком рівняння

 

 Дане рівняння має тільки один корінь – 12. Але є рівняння, що можуть мати два три і більше коренів або взагалі не мають коренів.

 

Розв'язати рівняння -  означає знайти всі  його корені або показати, що їх немає

 

 Кожне рівняння має ліву і праву частини. Так, у рівнянні 3х-27 = 9  різниця  3х.-27 – це ліва частина, а число  9 – права.

      3х, – 27 , 9 – називаються членами цього рівняння.

 

У.Узагальнення і систематизація вивченого матеріалу

 

1.Усне розв'язування тренувальних вправ

- Які з чисел – 2,5;.5; 7,5 – є коренями рівняння (х – 6,5) (х + 1,5 ) = 9 ?

- Складіть будь – яке рівняння коренем якого є число – 15.

- Скільки коренів має рівняння х ( х – 2 ) ( 3 + х ) = 0 ?

- Чи має рівняння 7 + х = х розв'язки? Чому?

- Покажіть ліву  та праву частини рівняння 2х + 3 = 3х – 8 та назвіть його члени.

2.Навчальна гра «Відгадай задумане слово»

 

   На дошці заздалегідь заготовлена таблиця-ключ, що дозволяє знайти букви задуманого слова. Букви відповідають числам, які є коренями даних рівнянь. Рівняння необхідно розв'язувати по порядку.

 

х – 12 = 32; 6х = 3,6; -10х = 8;  х = 12;

-10 + х = 15; 2х + 5 =12; 1 -3х = 25.

 

            Ключ до розв'язання

 

-0,8  г

 44   а

 78   м

                     -2,5  д

 3,5  р

                      25   б

                      -8   а

  н

 36   е

  40  о

 0,6  л

 

Задумане слово «АЛГЕБРА».

 

3.Розв'язування задачі за допомогою складання рівнянь

 

     На безлюдному острові Робінзон Крузо навчив рахувати свого папугу від 1 і до якогось числа. Якби це число подвоїти і до результату додати 30, то дістали б півсотні. До якого числа навчився рахувати папуга Робінзона Крузо?

     Рівняння до задачі складається колективно, але розв'язують його учні самостійно.

УІ. Підсумок уроку

 

Інтерактивна вправа «Незакінчені речення»

 

   Учитель формує незакінчене речення і пропонує учням висловитися щодо підсумку уроку, закінчуючи його. Кожний наступний учасник обговорення повинен починати свій виступ із запропонованої формули. Учні працюють з відкритими реченнями: «На сьогоднішньому уроці ми дізналися…», «На сьогоднішньому уроці найважливішим відкриттям для мене було…» та «На початку уроку я поставив перед собою мету. Ось як я її досягнув…»

 

УІІ. Домашнє завдання

1.Повторити правила знаходження невідомих компонентів арифметичних  дій.

2.При якому значенні змінної х значення виразів -11х + 2 і 9 – 21 рівні між собою?

3.Знайдіть суму коренів рівнянь.

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

ТЕМА.   Переставна властивість додавання.

Вправи на засвоєння таблиць додавання і 

віднімання в межах  10.

 

МЕТА. Зміцнювати вміння учнів використовувати під час обчислень переставну властивість додавання, продовжувати формувати вміння складати та розв’язувати задачі; вдосконалювати навички додавання та віднімання в межах 10; розвивати мислення, вміння аналізувати і робити висновки; виховувати почуття дружби, взаємодопомоги.

 

ОБЛАДНАННЯ: картина із зображенням ранньої весни. Грамзапис „ Голоси птахів” .Малюнки звірів: зайчика, вовчика, лисички, білочки. Малюнки птахів: ворони та сороки. Таблиці, картки.

 

                      ХІД  УРОКУ

І .Організаційна частина.

Ми починаємо урок,

Що математикою в нас

З любов'ю називається,

Вона нам допоможе

Таку розвинути точність думки,

Щоб у нашому житті

Про все дізнатися,

Виміряти, обчислити.

 

ІІ. Оголошення теми і завдань уроку.

•       Сьогодні на уроці ми повторимо таблиці додавання і віднімання в межах 10. Пригадаємо переставну властивість додавання, яку ми часто використовуємо при обчисленнях.

       Щоб добре все знати,

       Ми будемо міркувати,

       А  також рахувати,

       Задачі розв’язувати,

       Свій розум розвивати.

Будьте уважні, активні та дружні, бо дружба – то велика сила.

 

ІІІ. Повторення й узагальнення вивченого матеріалу.

•       Яка зараз пора року? ( Сніжна, морозна зима ).
•       За зимою прийде дивовижна весна. ( Картина )

Наше життя звеселить дзвінкий спів пташок.

 ( Грамзапис „ Голоси птахів”).

•       І  ось весняним лісом іде Червона Шапочка в гості до бабусі.

Раптом десь взялася Ворона Каркарона.

•       Кар-кар! Будь обережна! Будь обережна!
•       Але Червона Шапочка була не тільки доброю,

а й сміливою  дівчинкою. Дуже вона любила свою бабусю і хотіла її пригостити пиріжками.

Тож не слухала вона Ворони і прямувала вперед.

•       Діти! Напевно, недаремно застерігала Каркарона довірливу дівчинку. А раптом щось лихе станеться з Червоною Шапочкою? Проведемо її і, якщо потрібно буде, допоможемо. Отже, в дорогу.

1.   Хвилинка каліграфії.

•       Назвіть весняні місяці.
•       Якими цифрами позначені вони за календарем? (3,4,5).
•       Запишіть ці цифри в зошиті.
•       Визначте міс-трійку, міс-четвірку, міс-п’ятірку, для цього обведіть їх квадратиками.

 

                                 Цифри писатиму рівнесенько,

                                 Щоб були вони гарнесенькі,

                                 Щоб залюбки дивилась я.

                                 Вчителька й моя сім’я.

•       Дійсно, приємно мені дивитися. Як ви красиво і каліграфічно пишете.
•       Що ви можете сказати про ці числа?

( Одноцифрові, кожне наступне більше від попереднього на 1, а кожне попереднє менше від наступного на 1, 4 – парне. Їх сума дорівнює 12 ).

•       Із цими числами складіть приклади на додавання.
•       Яку властивість додавання використали при складанні прикладів?
•       Коли Ворона побачила, як ви гарно пишете, почула, як ви відповідаєте, то зрозуміла, що ви не залишите дівчинку в біді.

2.   Усні обчислення.

•       Ось летить Сорока-білобока.
•       Не йди в ту сторону, бо там чекає небезпека – каже вона Червоній Шапочці.
•       А куди ж іти? – запитує дівчинка.
•       Я скажу, але виконай з допомогою учнів таке завдання ( унаочнення ):

 

 

 

 

 

 

 

 

 

 

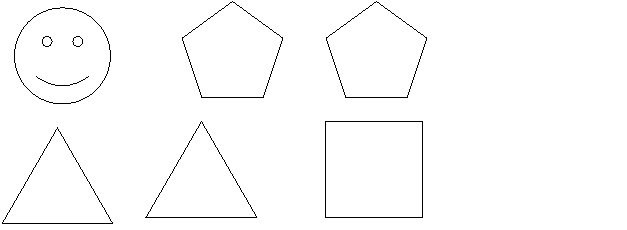
•       Які геометричні фігури ви бачите? Доведіть, що це за відрізки.
•       Знайдіть суму чисел у колах.
•       Знайдіть суму чисел у п’ятикутниках.
•       Знайдіть різницю чисел у трикутниках.
•       На скільки більше число у квадраті за число у прямокутнику?
•       На скільки один відрізок коротший від іншого?
•       Молодці – сказала Сорока-білобока і вказала дівчинці безпечну дорогу.

3.Математичний диктант.

   - Ось на дереві добра Білочка  горішки гризе.

Один упав під ноги Червоній Шапочці і розколовся. А там завдання. Прочитала дівчинка і просить допомогти їй написати математичний диктант:

      7 збільшити на 2;

      знайти суму чисел 5 і 3;

      8 зменшити на 4;

      на скільки 8 < від 10 ?

     на скільки  4 < від 9?

ПЕРЕВІРКА.

•       Дуже вдячна вам Червона Шапочка за допомогу, але вона стомилася і присіла на галявині відпочити. Відпочинемо і ми.

ФІЗКУЛЬТХВИЛИНКА  для очей.

1.   Робота з нерівностями та рівностями.

•       А ось сумує Зайчик. Він не може поставити потрібні цифри та знаки. Вухань звернувся по допомогу до Червоної Шапочки, а вона звернулася до вас. Допоможіть!

5 +4 *   4+5              5+2=  *   +5 

6+2  *   2+6              8+1= 1 +   *      

7+3   *  7+2              3+4=   *  +  *

ПЕРЕВІРКА. (Написати зі зворотної сторони дошки, а провести самоперевірку).

2.   Робота над задачею.

Ось і Лисичка. Вона не може скласти та розв’язати  задачу з підручника.

•       Що зображено на малюнку?
•       Людину, яка виготовляє діжки, називають бондарем.
•       Складіть задачу за малюнком. ( Діти складають задачу про бондаря, який виготовляє діжки, та розв’язують її).
•       Дуже вдячна Лисичка побігла далі.

3.   САМОСТІЙНА  РОБОТА. Робота на картках.

•       У Вовчика два ключі, а яким відкрити будинок бабусі, він забув. Якщо ви самостійно виконаєте завдання, то наша улюблениця зможе потім сама підібрати потрібний ключ. (Завдання на картках).

 

                               ПЕРЕВІРКА.

•       Яким ключем відкриваються будинки, пофарбовані  темним кольором? (10)
•       Яким ключем відкриваються будинки світлого кольору?(5)
•       Віддав Вовчик ключі Червоній Шапочці.

Дівчинка відкрила двері й бабуся радо зустріла внучку та запропонувала поділитися пиріжками з вами. Діти, ви стали з Червоною Шапочкою справжніми друзями, бо друзі пізнаються в біді.

ІУ. ПІДСУМОК УРОКУ.

- Ми покидаємо цей казковий ліс. Під час подорожі я переконалася, що ви вправно вмієте обчислювати приклади в межах 10 , складати та розв’язувати задачі, вмієте міркувати – швидко, лічити – точно, відповідати – правильно.

     Діти, яку властивість додавання ви часто використовуєте при обчисленнях?

     Один видатний математик казав, що тим, хто знає математику, легко збагнути справжню красу природи.

      Отже, пізнавайте світ, вивчайте красу нашої рідної природи. Ви можете!

 

 

 

 

 

 

 

 

 

 

 

 

                                                                                                                                                                                                                                                                                                                                         Тема. Додавання і віднімання іменованих чисел, виражених у мірах довжини і маси.

Мета: ознайомити учнів з прийомами письмового додавання і віднімання   

           іменованих чисел, виражених в одиницях маси і довжини;

           закріплювати вміння додавати і віднімати багатоцифрові числа,

           розв`язувати задачі; розвивати у дітей мислення, кмітливість, зв`язне  

           мовлення, обчислювальні навички, вміння коментувати; виховувати

           в учнів інтерес до математичних знань, бережливе ставлення до

           тваринного світу, виховувати культуру праці.

Обладнання:таблиця, електротабло, ілюстративний матеріал.

                                                             Хід уроку

1. <<Щоденне повторення – міцніші знання>>.

               Закінчується осінь. Багато змін відбулося в живій і неживій природі та в довкіллі нашої школи. Але математика – наука точна, тому вона вимагає точних знань. Треба бути уважним, правильно мислити, добре запам`ятовувати. Починаємо ми з розумової розминки.

1.1. Математичний зоровий диктант.

   Записати числа, визначити в них усі десятки, сотні, тисячі, розрядні доданки.

        1 987                 98 123                123 789               456 789

( Взаємоперевірка)

1.2. Обчислювальний ланцюжок.

      Доданок 90, доданок 10, знайти суму, зменш на 80, зменш у 5 разів, збільш у9 разів, збільш на 700, зменш на 200, знайди різницю отриманого числа і 500, поділи на 6, знайди добуток отриманого числа і 9, на скільки треба збільшити, щоб отримати 100, знайди попереднє число, поділи на 5.

( Відповідь: 100,20,4,36, 736, 536, 36, 6, 54,46, 45,9)

1.3. Математичний диктант.

- До числа 500 додати різницю чисел 400 і 100.

- До суми чисел 120 і 3000 додати 280.

- Від числа 750 відняти суму 250 і 50.

- До різниці чисел 500 і 220 додати 120.

- Число 930 зменшити на суму 600 і 130.

- Число 140 зменшити на суму 90 і 50.

 

1.4. Математичний малюнковий диктант про <<братів наших менших>>.

              Запишіть цифрові дані.

• На одному автомобільному шосе гине за рік:

7 195 фазанів,

1 318 оленів,

120 000 зайців.

            Підкресліть, скільки всього сотень у цих числах. (71, 13, 1 200)

• Корінним жителем Північного Полюсу є білий ведмідь. Освоюючи цей край, людина винищила половину цих полярних гігантів, масою 1 100 кг. Масу ведмедя запишіть у тоннах і центнерах. ( 1 100 кг = 1т 100кг)
• Щоб нагодувати тигра, потрібно 30 кг м`яса, а шлунок вусатого кита вміщує 30 т їжі. У скільки разів більше може з`їсти кит, ніж тигр?

Записати виразом.

3 000 : 30 = 100 (раз)

• Із 8 600 видів птахів, що мешкають  нині на Землі, записані голоси лише половини. Запишіть вирази, голоси скількох птахів записані?

Інші чекають дослідників і охоронців, тобто –вас.

Як ми повинні ставитись до природи?

У статті 66 Конституції України записано: << Кожен зобов`язаний не заподіювати шкоди природі…>>

8 600 : 2=4 300 (пт.)

(Перевірка)

2. <<Старого не цурайтесь і нового навчайтесь>>.

2.1. Створення проблемної ситуації.

( Двоє учнів виконують інсценівку).

               Мальвіна йшла з магазину і наспівувала веселу пісеньку . Коли це на зустріч іде Буратіно. Буратіно запитав у Мальвіни:

• Що ти несеш у торбині?
• Цукерки,- відповіла Мальвіна.
• А скільки їх всього у тебе є?
• В одному кульку 3 кг320г , а в другому – 2 кг 450г . Якщо скажеш, скільки їх всього у мене, то я тебе пригощу.

           Задумався Буратіно: хочеться цукерок, але ж треба відповісти на  запитання Мальвіни .

• Діти, а може ми допоможемо Буратіно?

3 кг 320 г + 2 кг 240 г = 5 кг 560 г

Ось і допомогли Буратіно. Подивіться, як він зрадів, адже Мальвіна пригостить цукерками.

 

2.2. Оголошення теми й мети уроку.

         Саме на цьому уроці ми розглянемо тему <<Додаванняі віднімання іменованих чисел>>.

 

2.3. Пояснення вчителя (робота за таблицею).

           Числа , які виражають масу або довжину, можна додавати і віднімати письмово двома способами:

1) Додавати так, як вони записані у прикладі.

2) Замінити кожне число меншими одиницями вимірювання маси або довжини і виконати дії.

 

2.4.Первинне закріплення.

2.4. Фізкультхвилинка.

3. <<Є задача – буде й розв`язок>>.

      ( Задача № 360 – розв`язуємо з опорою на малюнкову умову).

• Чи можемо ми дати відповідь на запитання задачі?Чому?
• Що ми повинні знати,щоб дати відповідь?
• Складемо план розв`язання задачі.
• Що ми дізнаємося першою дією?
• Чи можемо ми далі взнати масу індика?Чому?

План розв`язування

1) Яка маса курки?

2) Яка маса курки і гуски разом?

2) Яка маса індика?

4)  Яка маса усіх птахів?

4. <<Щоб  знання не розгубити, треба нам їх закріпити>>.

4.1. Самостійне розв`язання прикладів за таблицею ( за варіантами).

(Взаємоперевірка в парах)

4.2. Робота над задачею.

Робота в мікрогрупах.

Завдання:записати коротку умову до задачі і розв`язати її.

1 учень – записує коротку умову.

2 учень – записує розв`язання.

3 учень – слідкує за виконанням, презентує роботу.

5. Підсумок уроку.

- Яку тему ми сьогодні вивчили?

- Які іменовані числа ми додавали і віднімали?

- Як можна додати і відняти іменовані числа?

6. Хвилинка розумової гімнастики.

      - Послухайте байку.

Йшли пустелею два верблюди. Один ніс мішок – 5 пудів солі, а другий – 5 пудів вати. Було дуже жарко. Вони втомилися і , побачивши річку, разом з мішками полізли у воду. Після купання верблюди пішли далі. В одного з них поклажа стала легшою, а в другого – важчою. Чому?

 ( Сіль розчинилась у воді, а вата увібрала в себе вологу)

 

 

 

 

 

 

 

 

 

Урок математики у 4 класі

 

 

 

 

 

 

 

 

 

 

Тема. Одиниці вимірювання довжини

Мета: навчити дітей використовувати знання про міри довжини, розвивати знання про сферу їх використання, познайомити з новими мірами довжини, збагачувати знання дітей, формувати пізнавальний інтерес, обчислювальні навички,  виховувати самостійність учнів.

 

                                                     Хід уроку

І  Вступне слово вчителя.

З  настанням осені відбулося багато змін в живій і неживій природі та в довкіллі нашої школи. А ось математика – наука точна, тому вона вимагає від нас точних знань. Треба бути уважними, працьовитими, правильно мислити, добре запам’ятовувати. Сьогодні у нас математичний практикум. Ми працюватимемо над темою – одиниці вимірювання довжини. Що нового ви б хотіли дізнатися на цьому уроці? Чого навчитися? (Учні ставлять перед собою мету. Я хочу вивчити міри довжини;  навчитися перетворювати міри довжини; я хочу дізнатися про нові одиниці вимірювання довжини; вчитися працювати самостійно і т.д. )Проведемо «Розумову розминку».

ІІ  Розумова розминка

1. Диференційовані завдання на повторення мір довжини.

4км=                                42см=                                   7м  4см=

6м=            дм                58дм=     м     дм                8км  30м=       

8дм=          см                 2900м=    км   м                 43дм=

19см=  дм   см              97мм=        см    мм           5м  6дм=

2. Усний рахунок.

Скільки разів треба відрізати канат довжиною 10м на частини по 2м?

Периметр квадрата 56см. Яка сторона квадрата?

 

 

Із Запоріжжя до Харкова  автобус вирушає о 12 годині. Через годину із Харкова до Запоріжжя виїжджає велосипедист, але він їде значно повільніше, ніж автобус. Хто з них буде ближче до Харкова під час зустрічі?

(Накреслити малюнок і підтвердити свою відповідь).

 

 

ІІІ  Робота над новим матеріалом.

1. Повідомлення учнів

  У далеку давнину було багато різних одиниць вимірювання довжини. Незручно було ними користуватися. Потрібні були нові одиниці вимірювання. І вчені їх створили. За найголовнішу одиницю вимірювання довжини було взято метр.

2. Метр – родоначальник великої родини одиниць вимірювання довжини:

       Дециметр                         кілометр

       Сантиметр

       Міліметр

3. Тепер старовинні одиниці вимірювання довжини порівнюють з родиною метра.                                                  

Аршин = 71см 1мм                          верста = 1км 071м   

Дюйм = 2см 5мм                              миля = 1км 600м

Фут = 30см 3мм                                 морська миля = 1км 850м

Ярд = 91см 4мм                                 сажень = 2м 13см 4мм

• Чи можна назвати ці міри довжини точним? Чому?
•  

4. Раніше порівнювали аршин з довжиною руки до плеча. Народне прислів’я говорить «Міряє свій аршин». Тобто судить про все тільки по собі, адже довжина руки у всіх різна.  Про надзвичайно проникливу людину говорять «бачить на три аршини під землю». Дюйм – величина великого пальця. Дюймовочка – крихітна дівчинка з казки Андерсена. Знання мір і самі міри довжини використовуються в казках, прислів’ях, але найчастіше їх використовують в різних галузях народного господарства.

ІУ  Закріплення нового матеріалу.

1. Розв’язування задач.

• Яка найвища вершина Українських Карпат? (Говерла – 2061м)
• Яка найвища вершина Кримських гір? (Роман-Кош – 1545м).
• Яке поставимо запитання, щоб порівняти висоту цих гір?

 

• Визначити за картою відстань від Вінниці до Києва. Використовуючи масштаб. Масштаб: 1см = 7 км. Визначити відстань від Києва до Харкова.

 

 

•  

 

                 Глибина проникнення  в грунт корінців цибулі  50см. Корені картоплі на 15см глибше, а                       цукрового буряка на 26см глибше, а корені люцерни у 3 рази більше. Яка глибина проникнення коренів?

Слово вчителя.

Дві з половиною років тому грецький мудрець Фалес визначив висоту однієї з єгипетських пірамід. Тобто, він вибрав час, коли його власна тінь дорівнювала його росту, і виміряв довжину тіні піраміди. Зрозуміло. Що в цей час висота піраміди дорівнювала довжині своєї тіні.

У  Самостійна робота

                                                    І варіант

Волга має довжину 3530км. Дніпро 2200км, а  Іртиш на 1482км коротший, ніж Волга і Дніпро разом. Яка довжина Іртиша?

                                               ІІ варіант

Перший поїзд проїхав 1350 км, а другий – 875км. А третій поїзд подолав відстань у 5 разів менше, ніж перший і другий разом. Яку відстань подолав третій поїзд?

УІ Рефлексія. Гра «мікрофон».

• Над якою темою ми працювали на уроці?
• Що нового дізналися на уроці?

Сьогодні ми познайомилися з використанням мір довжини в різних галузях народного господарства, дізналися про одиниці вимірювання в давнину. Навчилися перетворювати одиниці вимірювання, розв’язували задачі, які містять одиниці вимірювання довжини.

•  Ще в багатьох галузях використовуються вони: в легкій промисловості – покрій та пошиття одягу.

 На 7 сорочок витратили 14м тканини. Скільки витратили тканини на 9 таких сорочок?

Будівництво – будують будинки,  дороги, метро, роблять вікна, двері.

Важка промисловість – виготовлення деталей до машин, верстатів, рейок для залізничної дороги.

  Знайомство з практичним використанням мір довжини ми продовжимо на наступних уроках.

УІІ  Це цікаво

    На якій висоті літають птахи (таблиця)

Шпак – 50 – 100м;

Дрібні птахи – до 100м;

Голуб – 90м;

Хижаки – 100м – 400м;

Великий лісовий голуб – 2400м;

Ворона – до 2500м;

Журавель – до 4500м.

УІІІ Підсумок. Домашнє завдання

• Для чого ми вивчаємо міри довжини?
• Де вони використовуються7
• Де ви користуєтеся знаннями про міри довжини?

 

 

 

ВИСНОВОК

Інноваційні технології навчання сприяють творчому засвоєнню знань. При цьому навчальний процес характеризується високою інтенсивністю, супроводжується підвищеним інтересом, одержані знання відрізняються глибиною та міцністю.

  Сучасний урок – це мистецтво поєднання методик та прийомів, які дають змогу Учителю відкрити Учню самого себе й само реалізуватися.

  Ми вважаємо себе щасливими людьми, бо бачимо в очах своїх учнів відблиск несподіваної думки і радість пізнання, здивування від власної імпровізації та творчості. Кожний урок для нас – це надія на маленьке відкриття в результаті щиросердного єднання з дітьми.

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

ВИСНОВОК

 

Дані розробки уроків показують взаємодію  роботи вчителя і учнів, під час якої реалізуються навчально-виховні можливості, викладені у змісті навчального матеріалу. Використані нами нетрадиційні форми  та методи організації роботи на різних етапах уроку показують організацію та практичне застосування побудови цих етапів. Вони є засобом підтримання інтересу учнів до вивчення математики; усвідомлення можливості розвивати свої розумові здібності та, взагалі, навчатися із задоволенням.

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

СПИСОК ВИКОРИСТАНИХ ДЖЕРЕЛ І ЛІТЕРАТУРИ

 

1.  Губа  Л.А. Нетрадиційні уроки. Харків: Вид.  Група „Основа”, 2005.

                     2.  Овечкіна О.І. Прийом активізації пізнавальної 

                          діяльності // Математика в школі.-1993.-№5.

3. Коваленко В.Г. Дидактичні ігри на уроках 

     математики. -  1990.

                      4. Пометун О.І., Пироженко Л.В. Сучасний урок.      

                          - 2004.

                      5.Карпінська  І.Й. Нестандартні уроки з  

                         математики. 9-11 клас. Тернопіль:

                         „Підручники і посібники”,2000.

                      6.Маркова І. С. Дидактичні ігри на уроках 

                          математики. 5-6 класи.. Харків: Вид. Група 

                       „Основа”, 2006  

                      7.Маркова І.С. Інтерактивні технології на уроках 

                         математики. Харків: Вид. Група „Основа”, 2009