Використання методу інтервалів при розв'язуванні ірраціональних, показникових та логарифмічних нерівностей

 

 

Автори:

 

Вчитель вищої кваліфікаційної категорії:

Морозюк Володимир Миколайович

 

Вчитель другої кваліфікаційної категорії:

Колісниченко Володимир Миколайович

У шкільному курсі математики розв’язуються досить складні (ірраціональні, показникові та логарифмічні) нерівності, але у підручниках підходи до їх розв’язування досить однобокі. Розглянемо кілька прикладів.

Наприклад, у підручнику [1] розглядаючи ірраціональні нерівності поділяють їх на типи:

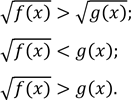1)

2)

3)

З одного боку це корисно, учням надається змога подумати над причинами виникнення кожної з наведених умов і чому, здавалося б необхідна умова, відсутня. Однак, розв’язувати вказаним методом ірраціональні нерівності дуже незручно, особливо нерівності третього типу [1, приклад 3, ст. 108].

Розв’яжіть нерівність   

Розв’язання: Дана нерівність рівносильна сукупності двох систем.

 

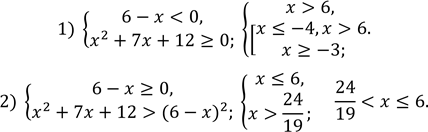
Відповідь: .

Виникає питання, а чому б не розв’язати цю нерівність методом інтервалів. Зробимо це

Розв’яжіть нерівність   

Розв’язання.

  

ОДЗ:  

Знайдемо нулі 

 

 

 

  

З цього слідує, що проміжок  взагалі розглядати не потрібно.

 

Знайдемо нулі

 

 

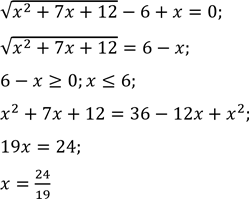
Встановивши знаки нерівності на проміжках, отримаємо   

Відповідь:  

Зауважимо, що точки  до відповіді включати не потрібно, оскільки вони не є нулями.

Хочемо звернути Вашу увагу на застосування методу інтервалів для розв’язування нерівностей у яких вводять заміну змінної. Всі автори підручників чомусь вводять заміну ще у самій нерівності, але чи варто це робити. Таке введення нової змінної призводить до того, що нулі знаходять для функції з новою змінною і, відповідно, розв’язки нерівності записують для функції нової змінної, а потім виникають складнощі з поверненням до попередньої змінної. А чому б не зробити заміну на етапі відшукання нулів функції, тоді, знайшовши нулі для нової змінної, ми відразу ж у рівняннях повертаємося до попередньої змінної і одержуємо нулі для функції зі змінною, заданою в умові.

Наведемо приклад розв’язаної задачі з підручника і покажемо як ми пропонуємо розв’язати її.   

Розглянемо приклад [2, ст. 176]

Розв’яжіть нерівність .

Розв’язання. Маємо:  Оскільки  при

будь якому , то поділивши обидві частини останньої нерівності на ,

отримуємо рівносильну нерівність .

Нехай . Тоді  Розв’язавши цю нерівність, отримуємо  Звідси: 

 

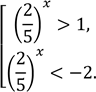
З нерівності . знаходимо, що  Нерівність . не має розв’язків. 

Відповідь:  

 Пропонуємо це завдання розв’язати так:

Розв’яжіть нерівність .

Розв’язання.

 

Знайдемо нулі

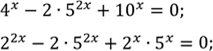
Очевидно, що  Поділивши, отримаємо

. 

Нехай .

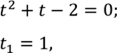
 не задовольняє обмеження.

Тобто .

 

Встановивши знаки нерівності на проміжках, отримаємо  

Відповідь:  

                Розглянемо приклад [2, ст. 218]       

Розв’яжіть нерівність 

 

Розв’язання. Оскільки областю визначення даної нерівності є проміжок

, то виконується рівність 

 

Тоді дану нерівність можна переписати так:

 

Нехай   Отримуємо:

 

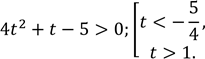
Маємо: 

 

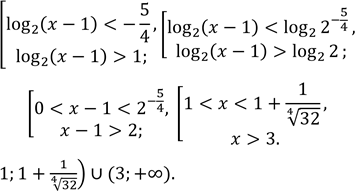
Відповідь: .

Пропонуємо такий спосіб розв’язання: 

Розв’яжіть нерівність 

 

Розв’язання.

ОДЗ:  

  .

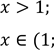
 Отже проміжок - взагалі розглядати не потрібно.

Знайдемо нулі

 

 

Нехай   

 

 

Тоді 

 

 

 

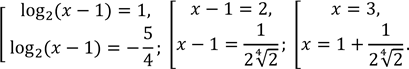
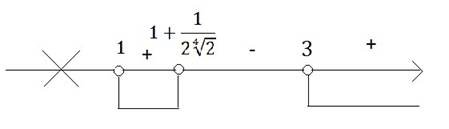
Встановивши знаки нерівності на проміжках, отримаємо 

 

Відповідь:   

Наведемо приклад ірраціональної нерівності, в якій зручно ввести заміну.

Розв’яжіть нерівність  

Розв’язання.   

 

 

ОДЗ: .

Знайдемо нулі

 

 

 

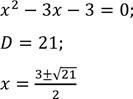
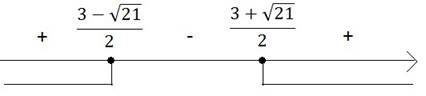
Знайдемо нулі

 

Зробимо заміну   тоді

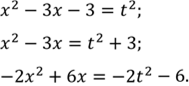
Отримаємо 

 

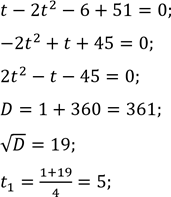
 не задовольняє обмеження.

 Повернемось до заміни

 

 

 

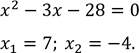
Встановивши знаки нерівності на проміжках, отримаємо 

  

Відповідь:    

Використаємо наведений метод для розв’язування [3, ст. 148]

 Знайдіть найбільший цілий розв’язок нерівності   

Розв’язання.

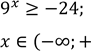
ОДЗ:  

Знайдемо нулі

 

Нехай  

 

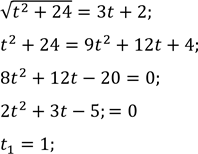
не задовольняє обмеження.

Повернувшись до заміни, отримаємо

 

Встановивши знаки нерівності на проміжках, отримаємо  Відповідь:  

                Розглянемо приклад [3, ст. 165]       

Знайдіть кількість цілих чисел, що не є розв’язкам   нерівності  

 

Розв’язання.

ОДЗ:  

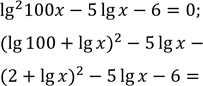
Знайдемо нулі

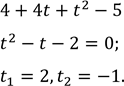
Нехай  

Повернувшись до заміни, отримаємо

 

 

 Встановивши знаки нерівності на проміжках, отримаємо

  

Відповідь: 100.

 

 

 

 

 

 

 

 

Список використаних джерел:

1.     Мерзляк А.Г., Алгебра і початки аналізу: проф. рівень: підручник для 10 кл. закладів загальної середньої освіти / А.Г. Мерзляк, Д.А.

Номіровський, В.Б. Полонський, М.С. Якір. – Х.: Гімназія, 2018. – 400 с. : іл.

2.     Мерзляк А.Г., Алгебра. 11 клас: підручник для загальноосвітніх навчальних закладів : академ. івень, проф. рівень/ А.Г. Мерзляк, Д.А.

Номіровський, В.Б. Полонський, М.С. Якір. – Х.: Гімназія, 2011. – 431 с. : іл.

3.     Математика. Комплексна підготовка до ЗНО і ДПА / Уклад.: А.М.

Капіносов [та ін.] – Тернопіль: Підручники і посібники, 2019. – 512с.