Зразки розв’язування завдань. Алгебраїчні рівняння та системи рівнянь.
Алгебраїчні рівняння та системи рівнянь.
-
Розв’язати рівняння
.
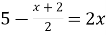Розв’язання:
Для розв’язання даного рівняння помножимо кожен із доданків на 2.
.
-
Розв’язати рівняння
.
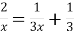Розв’язання:
Зведемо рівняння до спільного знаменника.
.
-
Розв’язати рівняння
.
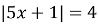Розв’язання:
Розкриємо модульні дужки.
-
Розв’язати рівняння
.
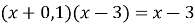Розв’язання:
Для розв’язання даного рівняння виконаємо множення у лівій частині рівняння і зведемо подібні доданки.
Відповідь: 0,9; 3.
-
Розв’язати рівняння
.
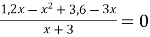Розв’язання:
Розкладемо чисельник на множники
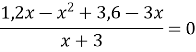
Скоротимо вираз на знаменник.
Відповідь; 1,2.
-
Розв’язати рівняння
.
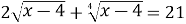Розв’язання:
Для розв’язання даного рівняння введемо заміну і розв’яжемо отримане квадратне рівняння.
Відповідь: 85.
-
Розв’язати рівняння
.
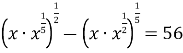Розв’язання:
Використаємо властивості степенів.
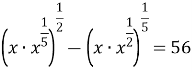
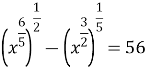
Введемо заміну
Повернемось до заміни
Відповідь: .
-
Розв’язати рівняння
.
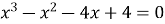Розв’язання:
По групуємо і винесемо спільні множники за дужки.
Розкладемо перший множник, як різницю квадратів
Відповідь: -2; 1; 2.
-
Розв’язати рівняння
.
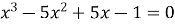Розв’язання:
Погрупуємо доданки.
Розкладемо вираз у перших дужках, як різницю кубів, а з других дужок винесемо спільний множник.
або
Відповідь: 
; 1; 
.
-
Розв’язати рівняння
.
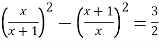Розв’язання:
Введемо заміну
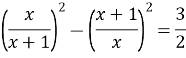
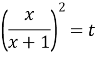
Повернемось до заміни
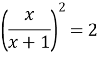
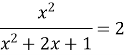
Відповідь: 
; 
.
- Знайти квадрат відстані між точками, що задовольняють систему рівнянь
.
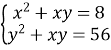Розв’язання:
Додамо перше рівняння системи до другого.
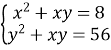
або
aбо
-
.
Відповідь: 200.
- Розв’язати систему рівнянь
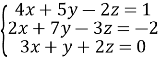
Розв’язання:
Для розв’язання даної системи рівнянь замінимо перше рівняння сумою першого і третього, а друге – сумою подвоєного другого і потроєного третього рівнянь.
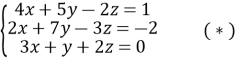
Помножимо перше рівняння на 13, а друге на 7 і знайдемо їх різницю.
1
З першого рівняння системи 
визначимо 
З першого рівняння системи 
визначимо 
1
Відповідь: (1; -1; -1)
-
Розв’язати рівняння
.
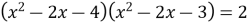Розв’язання:
Для того, щоб розв’язати дане рівняння, введемо заміну
Тоді рівняння набуде вигляду
За теоремою Вієта
Повернемось до заміни
;
або
.
-
Розв’язати рівняння:
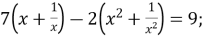
Розв’язання:
Для того, щоб розв’язати дане рівняння, введемо заміну
тоді 
Отримаємо рівняння
Повернемось до заміни
Ø
Відповідь: 0,5; 2.
-
Розв’язати рівняння
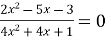
Розв’язання:
Розв’язання даного рівняння зводиться до розв’язання системи
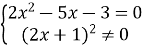
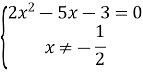
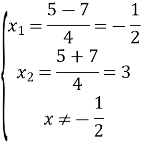
Відповідь: 
.
-
Розв’язати рівняння
.
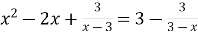Розв’язання:
-
Обчислити
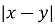, якщо 
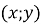розв’язки системи 
.
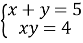Розв’язання:
.
- Визначити координати точки перетину прямих
і 
.
Розв’язання:
Знайдемо координати точки перетину заданих прямих розв’язавши систему рівнянь
Щоб розв’язати дану систему рівнянь скористаємось способом додавання
Відповідь: 
.
-
При якому значенні параметра а пряма
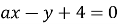проходить через точку 
.
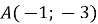Розв’язання:
Підставимо координати точки А у рівняння прямої, отримаємо
Відповідь: Пряма 
проходить через точку .
-
Обчислити
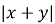, якщо 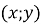розв’язки системи 
.
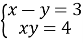Розв’язання:
-
Обчислити 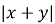, якщо 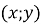розв’язки системи
.
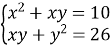Розв’язання:
Додамо рівняння системи
=6
-
Обчислити значення
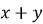, якщо 
.
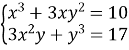Розв’язання:
Додамо рівняння системи
-
Обчислити добуток тих значень параметра а, при яких рівняння
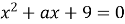має один корінь.
Розв’язання:
Рівняння має один корінь, коли його дискримінант рівний нулю.
-
Обчислити
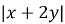, якщо 
.
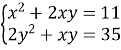Розв’язання:
-
Розв’язати рівняння
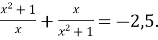
Розв’язання:
ОДЗ: 
.
Введемо заміну
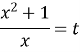
Повернемось до заміни
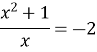
або
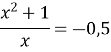
Ø
Відповідь: 
.
-
Знайти цілі розв’язки рівняння
.
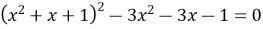Розв’язання:
Введемо заміну
Повернемось до заміни
або
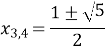
Відповідь: 
; 
-
Розв’язати у цілих числах систему рівнянь
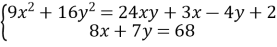
Розв’язання:
Для розв’язання даної системи, перенесемо у першому рівнянні усі доданки у ліву частину і по групуємо їх
Введемо заміну
Повернемось до заміни
Помножимо перше рівняння на 7, а друге на 4.
або
Помножимо перше рівняння на 8, а друге на 3
Відповідь: 
-
Обчислити
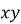, якщо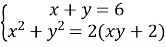 
Розв’язання:
Виконаємо множення у другому рівнянні , перенесемо вирази зі змінними у ліву частину та виділимо повний квадрат
або
Відповідь:
-
Знайти розв’язки рівняння
.
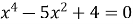Розв’язання:
Введемо заміну
За теоремою Вієта
.
Відповідь: -2; -1; 1; 2.
-
Обчислити 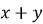, якщо
.
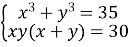Розв’язання:
Додамо до першого рівняння потроєне друге
Відповідь: .
про публікацію авторської розробки
Додати розробку