Зразки розв’язування завдань. Тотожні перетворення та обчислення значень арифметичних та алгебраїчних виразів.
Тотожні перетворення та обчислення значень
арифметичних та алгебраїчних виразів.
-
Обчислити
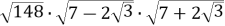 .
.
Розв’язання:
![]()
-
Обчислити
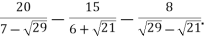
Розв’язання:
![]()
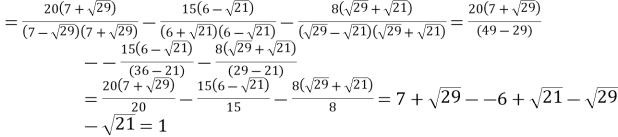 .
.
-
Обчислити
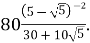
Розв’язання:
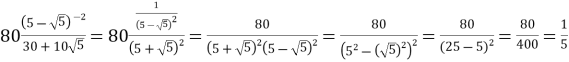 .
.
-
Обчислити
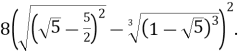
Розв’язання:
 .
.
-
Обчислити
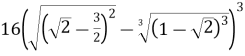 .
.
Розв’язання:
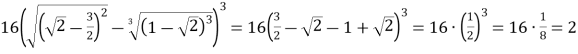 .
.
-
Обчислити
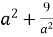 , якщо
, якщо 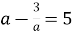 .
.
Розв’язання:
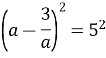
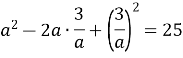
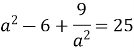
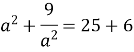
![]() .
.
- Знайти НСД та НСК чисел 75 і 125.
Розв’язання:
Розкладемо дані числа на прості множники
75=3·52 ;
125=53 ;
Щоб знайти НСД беремо спільні дільники чисел з найменшим показником степеня.
НСД(75, 125)=52=25
Щоб знайти НСК беремо всі дільники чисел, а спільні з найвищим показником степеня.
НСК(75,125)=3·53=375.
- Виконати дії:
![]() .
.
Розв’язання:
Спосіб 1:
Запишемо усі числа даного виразу у вигляді десяткових дробів і виконаємо дії.
![]() ;
;
Спосіб 2:
Запишемо усі числа даного виразу у вигляді звичайних дробів і виконаємо дії перетворюючи мішані числа у неправильні дроби і замінюючи ділення множенням на обернене число.
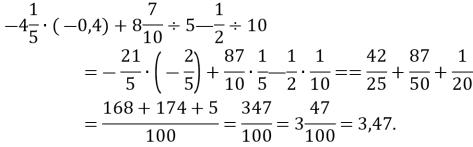
-
Знайти значення виразу
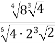 ;
;
Розв’язання:
Зведемо всі числа у чисельнику і знаменнику дробу під один знак кореня і виконаємо дії.
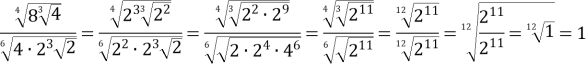
-
Знайти значення виразу:
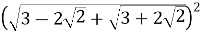 ;
;
Розв’язання:
Застосуємо до даного виразу формулу квадрату суми.![]()
![]()
![]() .
.
-
Знайти значення виразу:
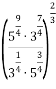 .
.
Розв’язання:
При розв’язуванні даного виразу застосуємо властивості степенів.
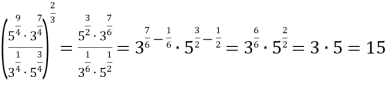 .
.
-
Знайти значення виразу
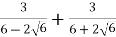 .
.
Розв’язання:
Зведемо даний вираз до спільного знаменника, це позбавить нас ірраціональності у знаменнику.
![]() .
.
-
Знайти значення виразу
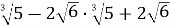 .
.
Розв’язання:
Перемножимо дані підкореневі вирази.
![]() .
.
- Довести, що дане число є натуральним.
![]() .
.
Розв’язання:
Щоб довести правильність даного твердження запишемо підкореневі вирази у вигляді повних квадратів і добудемо з них квадратні корені.
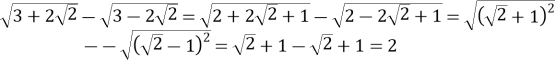 .
.
-
Обчислити
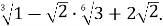
Розв’язання:
Для розв’язання даного виразу запишемо підкореневий вираз другого множника у вигляді квадрата двочлена.
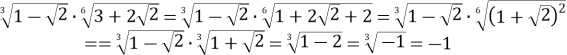 .
.
-
Обчислити
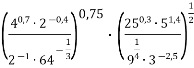 .
.
Розв’язання:
Запишемо усі числа з основою степеня у вигляді простих чисел.
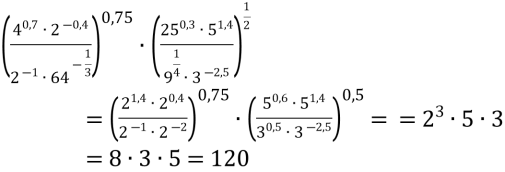 .
.
-
Спростити вираз
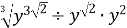 .
.
Розв’язання:
Для спрощення даного виразу застосуємо властивості степенів.
![]() .
.
-
Записати вираз у вигляді степеня
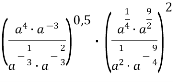 .
.
Розв’язання:
Для спрощення даного виразу застосуємо властивості степенів.
 .
.

про публікацію авторської розробки
Додати розробку
