Використання програми GEOGEBRA для розв’язання задач з параметрами
|
|
Міністерство освіти і науки України Рада директорів ВНЗ І-ІІ р. а. Херсонської області Херсонський політехнічний коледж Одеського національного політехнічного університету (базовий ВНЗ І-ІІ р. а. Херсонської області) |
|
|
|
Новокаховський приладобудівний технікум |
|
|
|
Методичне об’єднання викладачів математики
|
|
|
|
ВИКОРИСТАННЯ ПРОГРАМИ GEOGEBRA ДЛЯ РОЗВ’ЯЗАННЯ ЗАДАЧ З ПАРАМЕТРАМИ
для викладачів математики
|
|
|
|
Рекомендовано до друку методичною радою Новокаховського приладобудівного технікуму |
|
|
|
Протокол № 2 від 28.11. 2018 р.
|
|
|
|
Рекомендовано до друку методичним об'єднанням викладачів математики |
|
|
|
|
|
|
|
Херсон 2019
|
|
|
ВИКОРИСТАННЯ ПРОГРАМИ GEOGEBRA ДЛЯ РОЗВ’ЯЗАННЯ ЗАДАЧ З ПАРАМЕТРАМИ [Текст] / Уклад: І.В.Сушко — Нова Каховка: НКПТ, 2019. - 35 с. |
|
|
Навчальне видання
ВИКОРИСТАННЯ ПРОГРАМИ GEOGEBRA ДЛЯ РОЗВ’ЯЗАННЯ ЗАДАЧ З ПАРАМЕТРАМИ
|
|
|
Укладач |
І. В. Сушко, викладач вищої категорії, викладач-методист |
|
Відповідальний редактор:
|
І. В. Литвиненко, методист базового ВНЗ, методист вищої категорії Л. І. Опята, викладач вищої категорії, викладач-методист, Новокаховський політехнічний коледж ОНПУ |
|
Технічний редактор |
С.Ф.Башина, заступник директора з навчальної роботи НКПТ, викладач-методист
|
|
Рецензент |
Г.М.Біляєва завідувач денного відділення, викладач інформатики, викладач вищої категорії, викладач-методист |
|
|
За редакцією укладача Надруковано з оригінал-макета замовника
|
|
Підписано до друку 26.01.2018. Формат 600х840М1/16. Папір офсетний. Ум. друк. арк. 0,9. Гарнітура Times. Спосіб друку – ризографія. Тираж 4 прим. Зам. № __
73000, м. Херсон, вул. небесної сотні, 23 тел. (0552) 22-55-38, тел./факс (0552) 22-27-43 |
|
|
ЗМІСТ
|
||
|
Вступ ……………………………………………………………………. |
4 |
|
|
1. |
Інтерактивне геометричне середовище GeoGebra……………… |
6 |
|
2. |
Побудова динамічних об’єктів…………………………………… |
7 |
|
3. |
Приклади використання програми для розв’язування задач з параметрами………………………………………………………... 3.1. Задача №1……………………………………………………… 3.2. Задача №2……………………………………………………… 3.3. Задача №3……………………………………………………… 3.4. Задача №4……………………………………………………… 3.5. Задача №5 ……………………………………………………... |
9 12 18 21 24 27 |
|
4. |
Висновки…………………………………………………………… |
32 |
|
5. |
Список використаної літератури………………………………….. |
34 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Вступ
В сучасній освіті комп’ютерна техніка та Інтернет широко використовуються не тільки для вивчення інформатика, але і для вивчення інших предметів. Необхідність комп’ютерної підтримки освітнього процесу визначається сьогодні швидким розвитком інформаційних та комунікаційних технологій, проникненням їх у всі сфери життя, в тому числі і в сферу навчання, що обумовлює актуальність роботи.
Одним з напрямків роботи викладача математики є питання використання інформаційних технологій. На даний час розроблено достатньо багато програмних засобів для удосконалення освітнього процесу.
Кожному викладачу доводилося проводити підготовку своїх студентів до олімпіад різного рівня. В процесі розв'язування задач з параметрами, що містять графічний метод рішення, виникають дві проблеми: по-перше, правильно та доступно пояснити студенту суть даного методу, по-друге, потрібно вміти правильно відтворити математичну модель задачі за її умовними зображеннями для різних значень параметра.
На цьому етапі і випливає питання візуалізації розв'язування задачі. Це можливо зробити за допомогою олівця та лінійки. Для даного методу потрібно звичайно враховувати різні значення параметра, для яких задача має різні відповіді. На одному малюнку потрібно робити декілька графіків функцій, які відповідають різним значенням параметра, або навіть робити декілька малюнків. Специфіка рішення задач з параметрами вимагає використання програмних засобів.
Працюючи в необмежених просторах Інтернету, мою увагу привернула безкоштовна програма GeoGebra. Програма багатопрофільна. Вона може будувати графіки функцій та плоскі фігури на полотні 2D, об'ємні фігури та їх комбінації на полотні 3D та розв'язувати достатньо широкий клас задач. Програма допоможе при рішенні задач як шкільного курсу, так і задач з елементами вищої математики.
В даній навчально-методичній розробці розглянуто структуру програми GeoGebra, деякі аспекти роботи з нею та на прикладах розв’язку задач показано практичне її використання.
Навчально-методична розробка адресована:
- слухачам курсів підвищення кваліфікації викладачів математики;
- студентам та аспірантам, які цікавляться новими інноваційними технологіями та займаються самоосвітою;
- викладачам математики, які проводять підготовку студентів до олімпіад.
- Інтерактивне геометричне середовище GeoGebra.
Програма складається з головного меню, панелі інструментів, панелі об’єктів, графічного вікна та рядка введення.

Рис. 1
Головне меню – меню основних функціональних можливостей програми GeoGebra.
Панель інструментів – набір кнопок швидкого доступу до інструментів створення геометричних конструкцій в графічному вікні.
Графічне вікно – область для відображення геометричних конструкцій.
Панель об’єктів – область для відображення інформації про геометричні об’єкти, що входять до складу зображень в графічному вікні геометричної конструкції.
Рядок введення – поле для вводу алгебраїчних рівнянь, що задають геометричне місце точок. Після вводу алгебраїчного рівняння і натисканні клавіші Enter інформація про геометричний об’єкт відображається в панелі об’єктів, а сам геометричний об’єкт зображується в геометричному вікні.
- Побудова динамічних об’єктів.
Основною особливістю програми GeoGebra є можливість побудови динамічних об’єктів. Тобто, побудова геометричних конструкцій, які змінюються при зміні параметра ( параметрів ).
Інструментом, що дозволяє змінювати значення параметра в програмі GeoGebra є Повзунок ( Рис.2 )
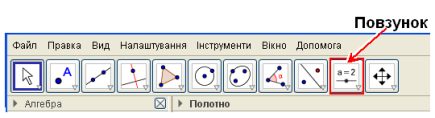
Рис. 2
Побудову динамічного об’єкта потрібно розпочати з натискання кнопки Повзунок на панелі інструментів. Після цього потрібно клацнути лівою кнопкою миші (в любому місці графічного вікна. В результаті з’явиться вікно діалогу Повзунок, в якому потрібно задати характеристики повзунка: тип параметра ( число, кут або ціле число ), ім’я параметра, мінімальне і максимальне значення параметра, величину шагу зміни параметра.
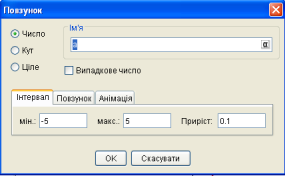
Рис. 3
Мінімальне і максимальне значення визначається областю дійсних значень параметра, визначених змістом поняття “довжина відрізка”, “величина кута”.
У випадку коли параметр буде визначатися значенням кута, то його область дійсних значень і крок зміни можуть бути задані як в градусах, так і в радіанах. По замовчуванню одиницею вимірювання є градус. Діалогове вікно дозволяє встановити деякі властивості повзунка. Для цього існують вкладки Повзунок та Анімація. ( Рис.4 )
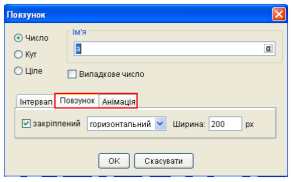
Рис. 4
На вкладці Повзунок можна вибирати варіант розміщення повзунка (горизонтальний або вертикальний) ( Рис.5 ).

Рис. 5
Дозволити чи заборонити його переміщення в графічному вікні за допомогою миші (прапорець закріплений), а також вибрати розміри повзунка (поле вводу Ширина).
Після визначення всіх характеристик повзунка потрібна нажати на Ок. В графічному вікні з’явиться зображення повзунка, а в панелі об’єктів символ та початкове його значення ( Рис.6 ).
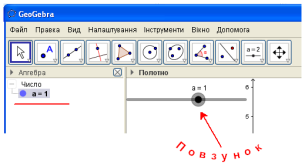
Рис. 6
Для зміни початкового значення параметра потрібно скористуватися інструментом Переміщення ![]() . Після вибору інструмента потрібно захватити точку на повзунку та змінювати відповідне значення параметра ( Рис.7 ).
. Після вибору інструмента потрібно захватити точку на повзунку та змінювати відповідне значення параметра ( Рис.7 ).

Рис. 7
Параметри, що задаються повзунком, можуть бути використані в описі геометричних фігур за допомогою рівнянь. Для цього в рядок введення достатньо записати рівняння, що містить цей параметр та нажати Enter. Крім цього, параметри можна використовувати для побудови геометричних фігур та конструкцій за допомогою елементів панелі інструментів.
Числові параметри використовуються наступними інструментами:
- Відрізок заданої довжини ( параметр – довжина )
- Коло за центром та радіусом ( параметр – радіус )
- Гомотетія відносно точки ( параметр – коефіцієнт гомотетії )
Параметри, що визначають величину кута, можна використовувати в наступних інструментах:
- Кут заданої величини (кутовий параметр – величина кута)
- Поворот навколо точки (кутовий параметр – кут повороту)
Продемонструємо використання повзунка для побудови динамічної фігури на прикладі кола з центром, абсциса і ордината якого можуть змінюватися в межах від -5 до 5, та із радіусом, діапазон якого можна змінювати в межах від 1 до 7.
Для реалізації даної побудови в програмі GeoGebra спочатку створимо повзунок, який відповідатиме за зміну радіуса (R) кола від 1 до 7 з кроком 0,1. Після цього вибираємо в панелі інструментів Коло за центром та радіусом, указуємо за допомогою миші в довільному місці графічного вікна точку, яка буде центром кола, а потім в діалоговому вікні Коло за центром та радіусом в полі для введення Радіус указуємо параметр R. ( Рис.8 )

Рис. 8
Тепер потрібно добавити ще два повзунка, які будуть відповідати за зміну абсциси ( параметр а ) і ординати ( параметр в ) центра кола. Після цього в панелі об’єктів нажати правою кнопкою миші на об’єкт Точка А і в контекстному меню вибрати Властивості… , що приведе до появи діалогового вікна. В рядку введення Визначення потрібно ввести найменування параметрів (a;b), що відповідають за абсцису і ординату точки А. ( Рис.9 )

Рис. 9
Таким чином, змінюючи значення повзунків, ми змінюємо три параметри a,b і R.
Те ж саме можна було отримати безпосереднім записом в рядок введення рівняння кола: (x-a)2+(y-b)2=R2
Тепер розглянемо використання програми для розв’язування задач, що містять параметри.
3. Приклади використання програми для розв’язування задач з параметрами.
ЗАДАЧА 1. Знайти всі значення параметра a, при яких функція ![]() зростає на R.
зростає на R.
1.Математичний розв’язок.
1) Розглянемо випадок коли ![]() , тобто
, тобто ![]() ,
, ![]() . Якщо
. Якщо ![]() , то функція має вигляд
, то функція має вигляд ![]() і є зростаючою функцією. Якщо
і є зростаючою функцією. Якщо ![]() , то функція має вигляд
, то функція має вигляд ![]() - парабола.
- парабола.
2) Нехай ![]() . Дослідимо функцію за допомогою похідної.
. Дослідимо функцію за допомогою похідної. ![]() .
.
![]() , коли
, коли ![]() ;
;

Дослідимо знак дискримінанта:

Якщо ![]() , то функція має дві екстремальні точки, тобто вона має проміжки зростання і спадання. Це дійсно для
, то функція має дві екстремальні точки, тобто вона має проміжки зростання і спадання. Це дійсно для ![]()
Якщо ![]() , то функція екстремальних точок не має. Це дійсно для
, то функція екстремальних точок не має. Це дійсно для ![]()
Нас цікавлять випадки коли ![]() для всіх значень
для всіх значень ![]() .
.
Графік функції ![]() є парабола, вітки якої направлені вверх.
є парабола, вітки якої направлені вверх. ![]() для
для ![]() Знайдемо координати вершини параболи
Знайдемо координати вершини параболи
![]()
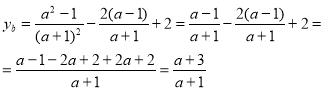
Нас цікавлять випадки коли ![]() . Тобто
. Тобто ![]() >0
>0
![]()
Це дійсно для ![]() Враховуючи початкові умови отримуємо для
Враховуючи початкові умови отримуємо для ![]()
3) У нас залишився випадок коли ![]() . Тоді
. Тоді ![]() і
і ![]() ,
, ![]()
Функція монотоно зростає.
2.Дослідження за допомогою програми GeoGebra.
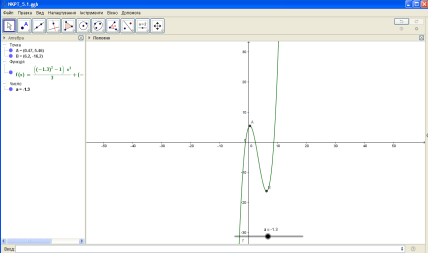
Рис. 1
а) на полотні розмістити повзунок ![]() ;
;
б) побудувати функцію з параметром ![]()
![]() та встановити екстремальні точки ( на графіку це точки А і В );
та встановити екстремальні точки ( на графіку це точки А і В );
в) дослідити розміщення функції для різних значень ![]() .
.
Висновки:
1) якщо ![]() - графік функції зростаюча квадратна гіпербола, екстремальних точок не має. ( Рис. 1.1)
- графік функції зростаюча квадратна гіпербола, екстремальних точок не має. ( Рис. 1.1)
2) якщо ![]() - монотонно-зростаюча квадратна гіпербола, одна екстремальна точка.
- монотонно-зростаюча квадратна гіпербола, одна екстремальна точка.
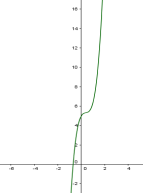
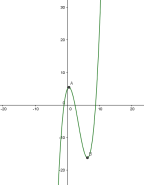
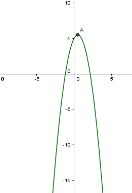
Рис. 1.1 Рис. 1.2 Рис. 1.3
3) якщо ![]() - графік функції має проміжки зростання і спадання, дві екстремальні точки. ( Рис. 1.2 )
- графік функції має проміжки зростання і спадання, дві екстремальні точки. ( Рис. 1.2 )
4) якщо ![]() - графік функції перетворюється в параболу. ( Рис. 1.3 )
- графік функції перетворюється в параболу. ( Рис. 1.3 )
5) якщо ![]() - квадратна гіпербола має проміжки зростання, спадання та дві екстремальні точки. ( Рис. 1.4 )
- квадратна гіпербола має проміжки зростання, спадання та дві екстремальні точки. ( Рис. 1.4 )
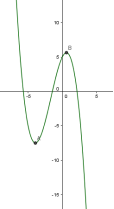
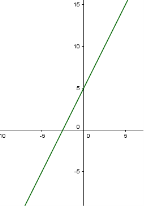
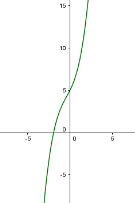
Рис. 1.4 Рис. 1.5 Рис. 1.6
6) якщо ![]() - функція перетворюється в зростаючу лінійну функцію. ( Рис. 1.5 )
- функція перетворюється в зростаючу лінійну функцію. ( Рис. 1.5 )
7) якщо ![]() - графік функції зростаюча квадратна гіпербола, екстремальних точок не має. ( Рис. 1.6 )
- графік функції зростаюча квадратна гіпербола, екстремальних точок не має. ( Рис. 1.6 )
Відповідь: функція зростає для ![]() та для
та для ![]() монотонно зростає.
монотонно зростає.
ЗАДАЧА 2. Знайти всі значення параметра a, при яких система рівнянь не має розв’язків. ![]()
1.Математичний розв’язок.
Система не матиме розв’язків, якщо ![]() . Тобто
. Тобто ![]() ;
; ![]() ;
; ![]() .
.
За теоремою Вієта ![]()
1) якщо ![]() , то
, то ![]() . Система має безліч розв’язків.
. Система має безліч розв’язків.
2) якщо ![]() , то
, то ![]() . Система не має розв’язків.
. Система не має розв’язків.
2.Дослідження за допомогою програми GeoGebra.
а) на полотні розмістити повзунок ![]() ;
;
б) побудувати графіки функцій з параметром ![]()
![]() та
та ![]() . Вибрати в меню точку перетину функцій;
. Вибрати в меню точку перетину функцій;
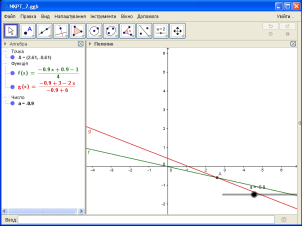
Рис. 2
в) змінюючи значення параметра ![]() за допомогою повзунка, розглянути різні випадки розміщення прямих.
за допомогою повзунка, розглянути різні випадки розміщення прямих.
Якщо ![]() обидва графіка співпадають. Тобто система має нескінчену кількість розв’язків.
обидва графіка співпадають. Тобто система має нескінчену кількість розв’язків.
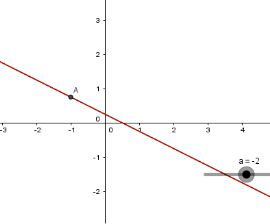
Рис. 2.1
Якщо ![]() графіки не перетинаються. Тобто система не має розв’язків.
графіки не перетинаються. Тобто система не має розв’язків.

Рис. 2.2
Для всіх інших значень параметра ![]() графіки лінійних функцій мають одну спільну точку.
графіки лінійних функцій мають одну спільну точку.
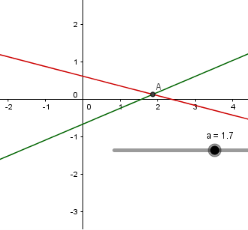
Рис. 2.3
Відповідь: система рівнянь не має розвязків для ![]() .
.
ЗАДАЧА 3. Знайти розв’язки рівняння  в залежності від параметра
в залежності від параметра ![]() .
.
1.Математичний розв’язок.
Побудуємо схематично графіки функцій  та
та ![]() для (
для ( ![]() ). Графік функції
). Графік функції ![]() є графіком спадної лінійної функції. Графік функції
є графіком спадної лінійної функції. Графік функції  є зростаюча крива, найменше значення якої є точка
є зростаюча крива, найменше значення якої є точка ![]() .
.

Рис. 3
Найменший розв’язок буде коли функція ![]() проходить через точку
проходить через точку![]() . Тобто
. Тобто ![]()
![]() . Значить для всіх
. Значить для всіх ![]() завжди буде єдиний розв’язок.
завжди буде єдиний розв’язок.
Знайдемо його.
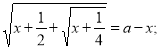

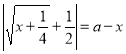 .
.
Так як ![]() , то
, то
![]()
![]()
Візьмемо праву і ліву частини рівняння в 2-у степінь.
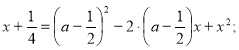
![]()
![]()
![]()
![]()
![]() .
.
Так як ![]()
![]() , то
, то ![]() - зайвий корінь.
- зайвий корінь.
2. Дослідження за допомогою програми GeoGebra.
а) на полотні розмістити повзунок ![]() ;
;
б) побудувати графік функції з параметром ![]()
![]() та
та ![]() . Вибрати в меню точку перетину функцій;
. Вибрати в меню точку перетину функцій;

Рис. 3.1
в) змінюючи значення параметра ![]() за допомогою повзунка, розглянути різні випадки розміщення графіків.
за допомогою повзунка, розглянути різні випадки розміщення графіків.
Програма не дає можливості знайти загальну формулу розв’язку рівняння, але вона допомагає проаналізувати для яких значень параметра ![]() графіки функцій перетинаються, тобто рівняння має єдиний розв’язок.
графіки функцій перетинаються, тобто рівняння має єдиний розв’язок.
Відповідь: ![]() для
для ![]() .
.
ЗАДАЧА 4. При якому значені параметра ![]() відстань між вершинами парабол
відстань між вершинами парабол ![]() і
і ![]() є найменшою.
є найменшою.
1. Математичний розв’язок.
Знайдемо координати вершини параболи ![]()
![]()
![]()
![]()
Знайдемо координати вершини параболи ![]()
![]()
![]()
![]()
Визначимо відстань між вершинами парабол
![]()
Проведемо дослідження функції ![]() та знайдемо її мінімальне значення.
та знайдемо її мінімальне значення.
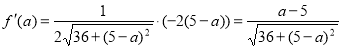

![]()
![]() - локальний мінімум. Якщо
- локальний мінімум. Якщо ![]() , то відстань між вершинами парабол
, то відстань між вершинами парабол ![]()
2. Дослідження за допомогою програми GeoGebra.
а) на полотні розмістити повзунок ![]() ;
;
б) побудувати графіки функцій
![]() та
та ![]() .
.
в) В меню програми вибрати Extremum для графіків функцій. На рисунку це відповідно точки ![]() і
і ![]() .
.

Рис. 4
г) В меню програми вибрати “Відрізок” і з’єднуємо точки ![]() і
і ![]() . На панелі об’єктів це відрізок
. На панелі об’єктів це відрізок ![]() .
.
д) В меню програми вибрати “Налаштування”- “округлення”-“5 десяткових розрядів”.
е) перемістивши повзунок, знаходимо найменше значення відстані між вершинами парабол ![]() при
при ![]() .
.
Відповідь: ![]() при
при ![]() .
.
ЗАДАЧА 5. В залежності від значення параметра ![]() розв’язати рівняння
розв’язати рівняння ![]() .
.
- Математичний розв’язок.
Областю дійсних значень змінної ![]() є множина, що задовольняє системі нерівностей.
є множина, що задовольняє системі нерівностей.
![]()
Візьмемо праву і ліву частину рівняння в квадрат.
![]()
![]()
![]()
Якщо ![]() , тобто
, тобто ![]()
![]()
![]() , то рівняння розв’язків не має.
, то рівняння розв’язків не має.
Якщо ![]() , тобто
, тобто ![]() , то рівняння має один розв’язок
, то рівняння має один розв’язок ![]() , що задовольняє ОДЗ.
, що задовольняє ОДЗ.
Якщо ![]() , тобто
, тобто ![]() , то рівняння має два корені
, то рівняння має два корені ![]()
![]() .
.
Перевіримо чи задовольняють наші корені першій умові ОДЗ. Для ![]()
![]()
![]()
![]()
![]() Даний вираз дійсний для любого значення
Даний вираз дійсний для любого значення ![]()
Для ![]()
![]()
![]()
![]()
![]() Даний вираз дійсний для любого значення
Даний вираз дійсний для любого значення ![]()
Значить перша умова ОДЗ ніяких обмежень на корені не дає.
Перевіримо другу умову ОДЗ. Для ![]()
![]()
![]() Даний вираз дійсний для любого значення
Даний вираз дійсний для любого значення ![]()
Для ![]()
![]()
![]()
![]()
![]()
![]()
Тобто для ![]() корінь
корінь![]() не існує.
не існує.
Проаналізувавши розв’язок отримуємо відповідь.
Якщо ![]() , то рівняння розв’язків не має.
, то рівняння розв’язків не має.
Якщо ![]() , рівняння має один розв’язок
, рівняння має один розв’язок ![]()
Якщо ![]() , рівняння має два розв’язки
, рівняння має два розв’язки ![]()
![]()
2. Дослідження за допомогою програми GeoGebra.
а) на полотні розмістити повзунок ![]() ;
;
б) побудувати графіки функцій
![]() та
та ![]() .
.
в) змінюючи значення параметра ![]() за допомогою повзунка, розглянути різні випадки розміщення графіків.
за допомогою повзунка, розглянути різні випадки розміщення графіків.
Якщо ![]() , то рівняння розв’язків не має.
, то рівняння розв’язків не має.
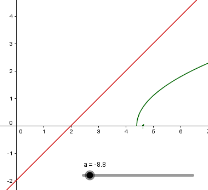
Рис. 5.1
Якщо ![]() , рівняння має один розв’язок
, рівняння має один розв’язок ![]()
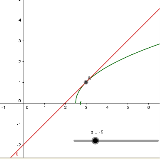
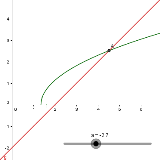
Рис. 5.2 Рис. 5.3
Якщо ![]() , рівняння має два розв’язки
, рівняння має два розв’язки ![]()
![]()

Рис. 5.4
Відповідь: 1) Якщо ![]() , то рівняння розв’язків не має.
, то рівняння розв’язків не має.
2) Якщо ![]() , рівняння має один розв’язок
, рівняння має один розв’язок ![]()
3) ![]() , рівняння має два розв’язки
, рівняння має два розв’язки ![]()
![]()
Висновки
Завдання з параметрами становлять хоч і невелику, але помітну частину математики. Матеріал, пов'язаний з рівняннями і нерівностями, що містять параметри, становить значну частину курсу. Це пояснюється тим, що рівняння і нерівності широко використовуються в різних розділах, при вирішенні важливих прикладних задач. Вивчення багатьох фізичних процесів і геометричних закономірностей часто призводить до вирішення завдань, що містять параметри. Сьогодні немає необхідності доводити актуальність теми «Завдання з параметрами» в рамках навчання математики. Також завдання з параметрами включені в завдання ЗНО. Вони часто бувають дуже складними і вимагають нестандартного підходу до вирішення.
На перших заняттях розв’язування завдань з параметрами, не потрібно примушувати студента розв'язувати задачі графічними методами. Необхідно дати йому можливість самостійного вибору методу вирішення тієї чи іншої задачі (функціонального або аналітичного). І тільки після цього, на прикладах в порівнянні з аналітичним або функціональним методами показати переваги графічного методу, того що використання цього методу в сукупності часто спрощує і скорочує час вирішення того чи іншого завдання з параметром.
GeoGebra це відмінний інструмент, який дозволить не просто урізноманітнити заняття з математики, а підвищити рівень якості розв’язування задач.
Використання програми GeoGebra на заняттях дозволяє:
- оптимізувати навчальний процес, більш раціонально використовуючи час;
- здійснювати диференційований підхід в навчанні;
- проводити індивідуальну роботу, використовуючи персональні комп'ютери;
- розширювати кругозір студентів;
- сприяє розвитку пізнавальної активності студентів.
Прогнозовані ефекти від застосування даної технології:
- можливе підвищення інтересу до досліджуваного предмета;
- підвищення рівня самооцінки;
- розвиток навички самоконтролю;
- спонукання до відкриття і вивчення нового в сфері інформаційних технологій.
Список використаних джерел
- Горошко Ю. В. Використання комп’ютерних програм для створення динамічних моделей при вивченні математики / Ю. В. Горошко, Є. Ф. Вінниченко // Науковий часопис НПУ імені М. П. Драгоманова. Серія №2. Комп’ютерно- орієнтовані системи навчання: зб. наук. праць / К. : НПУ імені М. П. Драгоманова, 2006. — № 4 (11). — С. 56–62.
- Горошко Ю. В. Розв’язування задач з параметрами за допомогою програми «GRAN-1». / Горошко Ю. В., Вінниченко Є. Ф. // Математика в школі. — 2008. — № 7–8(84).
- Грамбовська Л. В. Комп’ютерні динамічні моделі як засіб дидактичного забезпечення процесу навчання геометрії в сучасній школі. / Грамбовська Л. В., Яковчук О. М. // Комп'ютер у школі та сім'ї. — 2010. — № 7. — С. 14–17.
- Друшляк М. Г. Комп’ютерні інструменти програм динамічної математики і методичні проблеми їх використання / М. Г. Друшляк, О. В. Семенихіна/ / Інформаційні технології і засоби навчання, 2014, Том 42, №4.
- Жалдак М. І. Комп’ютер на уроках математики: посібник для вчителів. / Жалдак М. І. — Видання 2-е, перероблене та доповнене. — К. : РННЦ «ДІНІТ», 2003. — 324 с.
- Кушнір В. А. Розв’язування математичних задач інтегративного змісту засобами комп’ютерного моделювання. / Кушнір В. А., Ріжняк Р. Я. // Математика в школі. — 2009. — №10 (97).
- Ракута В. М. Бібліотека комп’ютерних моделей, як необхідна складова сучасного навчального середовища. / Ракута В. М. // Наукові записки. — Вип. 98. – Серія : Педагогічні науки. — Кіровоград: РВВ КДПУ ім. В. Винниченка, 2011. — С. 246–249.
- Ракута В. М. Програми для роботи з функціями та графіками. / Ракута В. М. // Комп'ютер у школі та сім'ї. — 2010. — № 7 (87). — С. 29–33.
- Ракута В.М. Система динамічної математики GEOGEBRA як інноваційний засіб вивчення математики / В.М.Ракута // Інформаційні технології і засоби навчання. 2012. №4 (30)
- Храповицкий И. С. Методические рекомендации по применению электронного учебного издания Geometer’s Sketchpad в учебном процессе общеобразовательных учреждений / Храповицкий И. С. – 2008. – 71 с.
- CABRILOG. Innovative Maths Tools [Електронний ресурс]. – Режим доступу: http://www.cabri.com.
- GeoGebra Wiki [Електронний ресурс]. – Режим доступу: http://www.geogebra.org.
Міністерство освіти і науки України
Рада директорів ВНЗ І-ІІ р. а. Херсонської області
Херсонський політехнічний коледж
Одеського національного політехнічного університету
(базовий ВНЗ І-ІІ р. а. Херсонської області)
Новокаховський приладобудівний технікум
Методичне об’єднання викладачів математики
ВИКОРИСТАННЯ ПРОГРАМИ GEOGEBRA ДЛЯ РОЗВ’ЯЗАННЯ ЗАДАЧ З ПАРАМЕТРАМИ
для викладачів математики
Рекомендовано до друку методичною радою Новокаховського приладобудівного технікуму
Протокол № 2 від 28.11. 2018 р.
Рекомендовано до друку методичним об'єднанням викладачів математики
Херсон 2019
ВИКОРИСТАННЯ ПРОГРАМИ GEOGEBRA ДЛЯ
РОЗВ’ЯЗАННЯ ЗАДАЧ З ПАРАМЕТРАМИ [Текст] / Уклад:
І.В.Сушко — Нова Каховка: НКПТ, 2019. - 35 с.
Навчальне видання
ВИКОРИСТАННЯ ПРОГРАМИ GEOGEBRA ДЛЯ РОЗВ’ЯЗАННЯ ЗАДАЧ З ПАРАМЕТРАМИ
|
Укладач |
І. В. Сушко, викладач вищої категорії, викладач-методист |
|
Відповідальний редактор:
|
І. В. Литвиненко, методист базового ВНЗ, методист вищої категорії Л. І. Опята, викладач вищої категорії, викладач-методист, Новокаховський політехнічний коледж ОНПУ |
|
Технічний редактор |
С.Ф.Башина, заступник директора з навчальної роботи НКПТ, викладачметодист |
Рецензент Г.М.Біляєва завідувач денного відділення, викладач інформатики, викладач вищої категорії, викладачметодист
За редакцією укладача
Надруковано з оригінал-макета замовника
Підписано до друку 26.01.2018. Формат 600х840М1/16.
Папір офсетний. Ум. друк. арк. 0,9. Гарнітура Times. Спосіб друку – ризографія. Тираж 4 прим. Зам. № __
![]()
Лабораторія організаційно-видавничої діяльності ХПТК ОНПУ
73000, м. Херсон, вул. небесної сотні, 23 тел. (0552) 22-55-38, тел./факс (0552) 22-27-43 ЗМІСТ
Вступ ……………………………………………………………………. 4
1. Інтерактивне геометричне середовище GeoGebra……………… 6
2. Побудова динамічних об’єктів…………………………………… 7
3. Приклади використання програми для розв’язування задач з
параметрами………………………………………………………... 9 3.1. Задача №1……………………………………………………… 12
3.2. Задача №2……………………………………………………… 18
3.3. Задача №3……………………………………………………… 21
3.4. Задача №4……………………………………………………… 24
3.5. Задача №5 ……………………………………………………... 27
4. Висновки…………………………………………………………… 32
5. Список використаної літератури………………………………….. 34
Вступ
В сучасній освіті комп’ютерна техніка та Інтернет широко використовуються не тільки для вивчення інформатика, але і для вивчення інших предметів. Необхідність комп’ютерної підтримки освітнього процесу визначається сьогодні швидким розвитком інформаційних та комунікаційних технологій, проникненням їх у всі сфери життя, в тому числі і в сферу навчання, що обумовлює актуальність роботи.
Одним з напрямків роботи викладача математики є питання використання інформаційних технологій. На даний час розроблено достатньо багато програмних засобів для удосконалення освітнього процесу.
Кожному викладачу доводилося проводити підготовку своїх студентів до олімпіад різного рівня. В процесі розв'язування задач з параметрами, що містять графічний метод рішення, виникають дві проблеми: по-перше, правильно та доступно пояснити студенту суть даного методу, по-друге, потрібно вміти правильно відтворити математичну модель задачі за її умовними зображеннями для різних значень параметра.
На цьому етапі і випливає питання візуалізації розв'язування задачі. Це можливо зробити за допомогою олівця та лінійки. Для даного методу потрібно звичайно враховувати різні значення параметра, для яких задача має різні відповіді. На одному малюнку потрібно робити декілька графіків функцій, які відповідають різним значенням параметра, або навіть робити декілька малюнків. Специфіка рішення задач з параметрами вимагає використання програмних засобів.
Працюючи в необмежених просторах Інтернету, мою увагу привернула безкоштовна програма GeoGebra. Програма багатопрофільна. Вона може будувати графіки функцій та плоскі фігури на полотні 2D, об'ємні фігури та їх комбінації на полотні 3D та розв'язувати достатньо широкий клас задач. Програма допоможе при рішенні задач як шкільного курсу, так і задач з елементами вищої математики.
В даній навчально-методичній розробці розглянуто структуру програми GeoGebra, деякі аспекти роботи з нею та на прикладах розв’язку задач показано практичне її використання.
Навчально-методична розробка адресована:
- слухачам курсів підвищення кваліфікації викладачів математики;
- студентам та аспірантам, які цікавляться новими інноваційними технологіями та займаються самоосвітою;
- викладачам математики, які проводять підготовку студентів до олімпіад.
1. Інтерактивне геометричне середовище GeoGebra.
Програма складається з головного меню, панелі інструментів, панелі об’єктів, графічного вікна та рядка введення.

Рис. 1 Головне меню – меню основних функціональних можливостей програми GeoGebra.
Панель інструментів – набір кнопок швидкого доступу до інструментів створення геометричних конструкцій в графічному вікні.
Графічне вікно – область для відображення геометричних конструкцій.
Панель об’єктів – область для відображення інформації про геометричні об’єкти, що входять до складу зображень в графічному вікні геометричної конструкції.
Рядок введення – поле для вводу алгебраїчних рівнянь, що задають геометричне місце точок. Після вводу алгебраїчного рівняння і натисканні клавіші Enter інформація про геометричний об’єкт відображається в панелі об’єктів, а сам геометричний об’єкт зображується в геометричному вікні.
2. Побудова динамічних об’єктів.
Основною особливістю програми GeoGebra є можливість побудови динамічних об’єктів. Тобто, побудова геометричних конструкцій, які змінюються при зміні параметра ( параметрів ).
Інструментом, що дозволяє змінювати значення параметра в програмі GeoGebra є Повзунок ( Рис.2 )

Рис. 2
Побудову динамічного об’єкта потрібно розпочати з натискання кнопки Повзунок на панелі інструментів. Після цього потрібно клацнути лівою кнопкою миші (в любому місці графічного вікна. В результаті з’явиться вікно діалогу Повзунок, в якому потрібно задати характеристики повзунка: тип параметра ( число, кут або ціле число ), ім’я параметра, мінімальне і максимальне значення параметра, величину шагу зміни параметра.
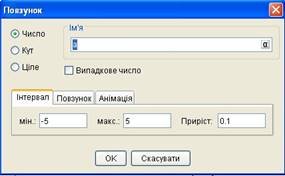
Рис. 3
Мінімальне і максимальне значення визначається областю дійсних значень параметра, визначених змістом поняття “довжина відрізка”, “величина кута”.
У випадку коли параметр буде визначатися значенням кута, то його область дійсних значень і крок зміни можуть бути задані як в градусах, так і в радіанах. По замовчуванню одиницею вимірювання є градус. Діалогове вікно дозволяє встановити деякі властивості повзунка. Для цього існують вкладки Повзунок та Анімація. ( Рис.4 )
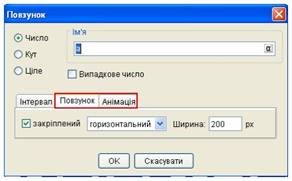
Рис. 4
На вкладці Повзунок можна вибирати варіант розміщення повзунка (горизонтальний або вертикальний) ( Рис.5 ).

Рис. 5
Дозволити чи заборонити його переміщення в графічному вікні за допомогою миші (прапорець закріплений), а також вибрати розміри повзунка (поле вводу Ширина).
Після визначення всіх характеристик повзунка потрібна нажати на Ок. В графічному вікні з’явиться зображення повзунка, а в панелі об’єктів символ та початкове його значення ( Рис.6 ).
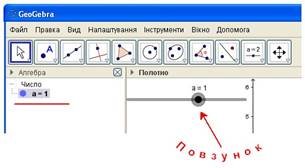
Рис. 6
Для зміни початкового значення
параметра потрібно скористуватися інструментом Переміщення ![]() .
Після вибору інструмента потрібно захватити точку на повзунку та змінювати
відповідне значення параметра ( Рис.7 ).
.
Після вибору інструмента потрібно захватити точку на повзунку та змінювати
відповідне значення параметра ( Рис.7 ).
Рис. 7
Параметри, що задаються повзунком, можуть бути використані в описі геометричних фігур за допомогою рівнянь. Для цього в рядок введення достатньо записати рівняння, що містить цей параметр та нажати Enter. Крім цього, параметри можна використовувати для побудови геометричних фігур та конструкцій за допомогою елементів панелі інструментів.
Числові параметри використовуються наступними інструментами:
• Відрізок заданої довжини ( параметр – довжина )
• Коло за центром та радіусом ( параметр – радіус )
• Гомотетія відносно точки ( параметр – коефіцієнт гомотетії )
Параметри, що визначають величину кута, можна використовувати в наступних інструментах:
• Кут заданої величини (кутовий параметр – величина кута)
• Поворот навколо точки (кутовий параметр – кут повороту)
Продемонструємо використання повзунка для побудови динамічної фігури на прикладі кола з центром, абсциса і ордината якого можуть змінюватися в межах від -5 до 5, та із радіусом, діапазон якого можна змінювати в межах від 1 до 7.
Для реалізації даної побудови в програмі GeoGebra спочатку створимо повзунок, який відповідатиме за зміну радіуса (R) кола від 1 до 7 з кроком 0,1. Після цього вибираємо в панелі інструментів Коло за центром та радіусом, указуємо за допомогою миші в довільному місці графічного вікна точку, яка буде центром кола, а потім в діалоговому вікні Коло за центром та радіусом в полі для введення Радіус указуємо параметр R. ( Рис.8 )
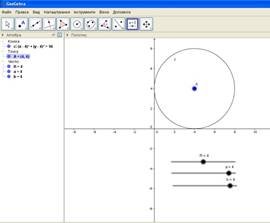
Рис. 8
Тепер потрібно добавити ще два повзунка, які будуть відповідати за зміну абсциси ( параметр а ) і ординати ( параметр в ) центра кола. Після цього в панелі об’єктів нажати правою кнопкою миші на об’єкт Точка А і в контекстному меню вибрати Властивості… , що приведе до появи діалогового вікна. В рядку введення Визначення потрібно ввести найменування параметрів
(a;b), що відповідають за абсцису і ординату точки А. ( Рис.9 )
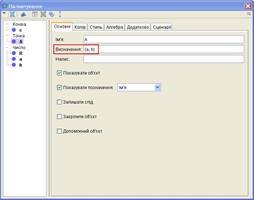
Рис. 9 Таким чином, змінюючи значення повзунків, ми змінюємо три параметри a,b і R.
Те ж саме можна було отримати безпосереднім записом в рядок введення рівняння кола: (x-a)2+(y-b)2=R2
Тепер розглянемо використання програми для розв’язування задач, що містять параметри.
3. Приклади використання програми для розв’язування задач з параметрами.
ЗАДАЧА 1. Знайти
всі значення параметра a, при яких функція f (x)= ![]() (a2 −1) x3 +(a−1)x2 +2x+5 зростає на R. 3
(a2 −1) x3 +(a−1)x2 +2x+5 зростає на R. 3
1.Математичний розв’язок.
1) Розглянемо випадок коли a2 −1= 0 , тобто a2 =1, a=1. Якщо a=1, то функція має вигляд f (x) = 2x + 5 і є зростаючою функцією. Якщо a=−1, то функція має вигляд f (x) = −2x2 + 2x +5- парабола.
2) Нехай a1. Дослідимо функцію за допомогою похідної.
f (x) = (a2 −1)x2 + 2(a −1)x + 2 .
f (x) = 0 , коли (a2 −1)x2 + 2(a −1)x + 2 = 0;
D = 4(a −1)2 − 4(a2 −1)*2 = 4(a −1)2 − 4(a −1)(a +1)*2 =
= 4(a −1)((a −1) − 2(a +1)) = 4(a −1)(a −1− 2a − 2) =
= 4(a −1)(−a −3) = −4(a −1)(a + 3)
Дослідимо знак дискримінанта:
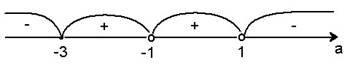
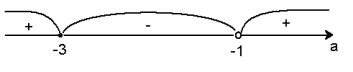
Якщо D 0, то функція має дві екстремальні точки, тобто вона має проміжки зростання і спадання. Це дійсно для a(−3;−1) (−1;1).
Якщо D0, то функція екстремальних точок не має. Це дійсно для a(−;−3) (1;+).
Нас цікавлять випадки коли f (x) 0 для всіх значень xR.
Графік функції f (x) є парабола, вітки якої направлені вверх.
![]() (a2 −1) 0 для a(−;−3) (1;+).Знайдемо координати
вершини параболи xb = −2(2a(2a−−11)) = − a1+1
(a2 −1) 0 для a(−;−3) (1;+).Знайдемо координати
вершини параболи xb = −2(2a(2a−−11)) = − a1+1
a2 −1 2(a−1) a−1 2(a−1)
![]()
![]() yb = (a+1)2 − a+1
+2= a+1− a+1
+2= a−1−2a+2+2a+2 a+3
yb = (a+1)2 − a+1
+2= a+1− a+1
+2= a−1−2a+2+2a+2 a+3
![]() = =
= =
a+1 a+1
a +3
Нас цікавлять
випадки коли yb 0 . Тобто ![]() >0
a +1
>0
a +1
(a + 3)(a +1) 0

Це дійсно для a(−;−3) (−1;+).Враховуючи початкові умови отримуємо для a(−;−3) (1;+).
3) У нас залишився випадок коли a=−3. Тоді
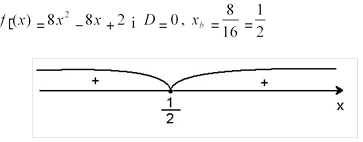
Функція монотоно зростає.
2.Дослідження за допомогою програми GeoGebra.
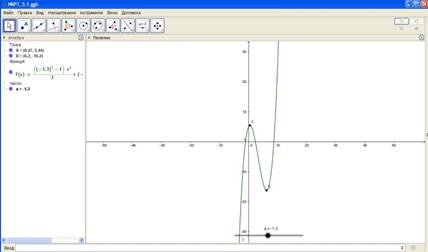
Рис. 1
а) на полотні розмістити повзунок a,a−50;50,h=0.1;
б) побудувати функцію з параметром a
![]() (a2 −1)
3 (a
−1)x2 + 2x+5 та встановити
екстремальні
(a2 −1)
3 (a
−1)x2 + 2x+5 та встановити
екстремальні
f (x) =x +
3
точки ( на графіку це точки А і В );
в) дослідити розміщення функції для різних значень a.
Висновки:
1) якщо a(−;−3) - графік функції зростаюча квадратна
гіпербола, екстремальних точок не має. ( Рис. 1.1)
2) якщо a=−3 - монотонно-зростаюча квадратна гіпербола, одна екстремальна точка.
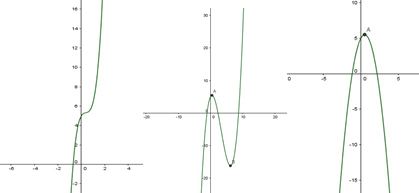
Рис. 1.1 Рис. 1.2 Рис. 1.3
3) якщо a(−3;−1) - графік функції має проміжки зростання і
спадання, дві екстремальні точки. ( Рис. 1.2 )
4) якщо a=−1 - графік функції перетворюється в параболу. ( Рис. 1.3 )
5) якщо a(−1;1) - квадратна гіпербола має проміжки зростання, спадання та дві екстремальні точки. ( Рис. 1.4 )

Рис. 1.4 Рис. 1.5 Рис. 1.6
6) якщо a=1 - функція перетворюється в зростаючу лінійну функцію. ( Рис. 1.5 )
7) якщо a(1;+) - графік функції зростаюча квадратна гіпербола, екстремальних точок не має. ( Рис. 1.6 )
Відповідь: функція зростає для a(−;−3) (1;+) та для a=−3 монотонно зростає.
ЗАДАЧА 2. Знайти всі значення параметра a, при яких
система рівнянь не має розв’язків. 2x+(a+6)y=a+3 ax−4y=a+1
1.Математичний розв’язок.
a1 b1 c1
Система не матиме розв’язків, якщо = . Тобто a2 b2 c2
![]() a = −4 a +1 2 6a = −8; a2 + 6a +
8 = 0. ; a
+
a = −4 a +1 2 6a = −8; a2 + 6a +
8 = 0. ; a
+
2 a +6 a +3
За теоремою Вієта a1 =−2,a2 =−4
a1 b1 c1
1) якщо
a1 =−2, то ![]() = = . Система має
безліч a2 b2 c2
= = . Система має
безліч a2 b2 c2
розв’язків.
a1 b1 c1
2) якщо a1 =−4, то = . Система не має розв’язків.
a2 b2 c2
2.Дослідження за допомогою програми GeoGebra.
а) на полотні розмістити повзунок a,a−5;5,h=0.1;
б) побудувати
графіки функцій з параметром a
f (x) = ![]() ax
−
a −1 та f (x)
=
ax
−
a −1 та f (x)
= ![]() −
2x + a +
3 . Вибрати в меню точку
−
2x + a +
3 . Вибрати в меню точку
4 a + 6
перетину функцій;
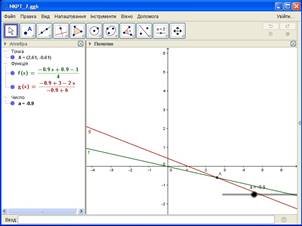
Рис. 2
в) змінюючи значення параметра a за допомогою повзунка,
розглянути різні випадки розміщення прямих.
Якщо a=−2 обидва графіка співпадають. Тобто система має нескінчену кількість розв’язків.

Рис. 2.1
Якщо a=−4 графіки не перетинаються. Тобто система не має розв’язків.
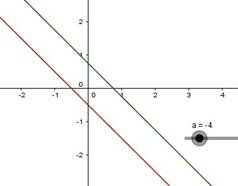
Рис. 2.2
Для всіх інших значень параметра a графіки лінійних функцій мають одну спільну точку.

Рис. 2.3
Відповідь: система рівнянь не має розвязків для a=−4.
ЗАДАЧА 3. Знайти розв’язки рівняння
![]() x+ + x+ =a−x в
залежності від параметра a.
x+ + x+ =a−x в
залежності від параметра a.
1.Математичний розв’язок.
 Побудуємо
схематично графіки функцій y=
x+ + x+ та y=a−x для ( a= 0). Графік функції y=a−x є графіком спадної
лінійної функції. Графік функції y=
x+ + x+ є
Побудуємо
схематично графіки функцій y=
x+ + x+ та y=a−x для ( a= 0). Графік функції y=a−x є графіком спадної
лінійної функції. Графік функції y=
x+ + x+ є
зростаюча крива, найменше значення якої є точка A(−![]() ;
;![]() ).
).

Рис. 3
Найменший розв’язок буде коли
функція y=a−x проходить через точку A(−![]() ;
;![]() ).
Тобто
).
Тобто ![]() = a +
= a + ![]() ;
a =
;
a = ![]() −
− ![]() =
= ![]() .
.
Значить для всіх a ![]() завжди
буде єдиний розв’язок.
завжди
буде єдиний розв’язок.
Знайдемо його.

Візьмемо праву і ліву частини рівняння в 2-у степінь.
![]()
![]()
![]() 1 a
− 1 2 − 2a
− 1 x + x2;
1 a
− 1 2 − 2a
− 1 x + x2;
x + =
4 2 2
x2 −2ax + x + a2 −a + ![]() − x −
− x − ![]() = 0; x2 − 2ax + a2 − a = 0;
= 0; x2 − 2ax + a2 − a = 0;
D = 4a2 −4(a2 −a) = 4a2 −4a2 +4a = 4a;
![]() 2a
+
2 a
2a
+
2 a
![]() x1 == a + a; x2 = a −
x1 == a + a; x2 = a −
2
![]() Так як a −
x 0;
xa , то x1 =a+ a - зайвий
корінь.
Так як a −
x 0;
xa , то x1 =a+ a - зайвий
корінь.
2. Дослідження за допомогою програми GeoGebra.
а) на полотні розмістити повзунок a,a−5;50,h=0.05;
б) побудувати графік функції з параметром a
f (x) = a − x та f (x) = sqrt(x +0.5+ sqrt(x +0.25)). Вибрати в меню точку перетину функцій;

Рис. 3.1
в) змінюючи значення параметра a за допомогою повзунка,
розглянути різні випадки розміщення графіків.
Програма не дає можливості знайти загальну формулу розв’язку рівняння, але вона допомагає проаналізувати для яких значень параметра a графіки функцій перетинаються, тобто рівняння має єдиний розв’язок.
![]() Відповідь:
x = a− a для a
Відповідь:
x = a− a для a ![]() .
.
ЗАДАЧА 4. При якому значені параметра a відстань між вершинами парабол y = x2 +8x+5 і y = 2x2 −8x + a + 2 є найменшою.
1. Математичний розв’язок.
Знайдемо координати вершини
параболи y = x2 +8x+5 xb = ![]() = −4; yb =16 −32 +15 = −1; A(−4;−1)
= −4; yb =16 −32 +15 = −1; A(−4;−1)
Знайдемо координати вершини параболи y = 2x2 −8x + a + 2
8
xb = ![]() = 2; yb =8−16+a+2 = a−6; B(2;a − 6) 4
= 2; yb =8−16+a+2 = a−6; B(2;a − 6) 4
Визначимо відстань між вершинами парабол
![]() AB
= (−4 − 2)2 + (−1− (a − 6))2 = 36 + (5 − a)2
AB
= (−4 − 2)2 + (−1− (a − 6))2 = 36 + (5 − a)2
![]() Проведемо
дослідження функції f (a) =
36 + (5 − a)2 та знайдемо її
мінімальне значення.
Проведемо
дослідження функції f (a) =
36 + (5 − a)2 та знайдемо її
мінімальне значення.
1 a −5
f (a) =(−2(5−a)) =
![]()
![]() 2
36+(5−a)2 36+(5−a)2
2
36+(5−a)2 36+(5−a)2

a= 5- локальний мінімум. Якщо a= 5, то відстань між
![]() вершинами
парабол AB = 36+(5−5)2 = 36 = 6.
вершинами
парабол AB = 36+(5−5)2 = 36 = 6.
2. Дослідження за допомогою програми GeoGebra.
а) на полотні розмістити повзунок a,a0;8,h=0.01;
б) побудувати графіки функцій
y = x^2 + 8 x + 5 та y = 2x^2−8x + a + 2.
в) В меню програми вибрати Extremum для графіків функцій.
На рисунку це відповідно точки A і B .
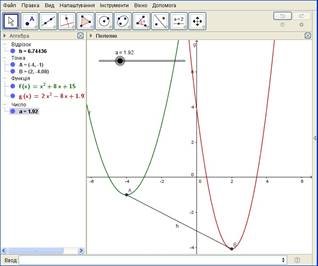
Рис. 4
г) В меню програми вибрати “Відрізок” і з’єднуємо точки A і B . На панелі об’єктів це відрізок h.
д) В меню програми вибрати “Налаштування”- “округлення”“5 десяткових розрядів”.
е) перемістивши повзунок, знаходимо найменше значення
відстані між вершинами парабол h=6 при a= 5.
Відповідь: h=6 при a= 5.
![]() ЗАДАЧА
5. В залежності від значення параметра a розв’язати рівняння 2x + a = x − 2.
ЗАДАЧА
5. В залежності від значення параметра a розв’язати рівняння 2x + a = x − 2.
1. Математичний розв’язок.
Областю дійсних значень змінної x є множина, що задовольняє системі нерівностей.
2x+a 0; x−2 0.
Візьмемо праву і ліву частину рівняння в квадрат.
2x + a = x2 − 4x + 4; x2 − 6x − a + 4 = 0; D=36−16+4a=20+4a.
Якщо D 0, тобто 20 + 4a 0; 4a −20; a−5, то рівняння розв’язків не має.
Якщо D= 0, тобто a=−5, то рівняння має
один розв’язок x =
![]() = 3, що задовольняє
ОДЗ.
= 3, що задовольняє
ОДЗ.
Якщо D0, тобто a−5, то рівняння має два корені
![]() x1 = 6+ 20+ 4a =
6+ 2
5+ a =
3+ 5+ a;
x1 = 6+ 20+ 4a =
6+ 2
5+ a =
3+ 5+ a;
2 2
![]() x2 = 3− 5+a .
x2 = 3− 5+a .
Перевіримо чи задовольняють наші корені першій умові ОДЗ.
![]() Для
x1 = 3+ 5+ a :
Для
x1 = 3+ 5+ a :

![]()
![]() 2(3+ 5+a) +a 0; 6+ 2 5+a +a 0; 5+a+ 2 5+a +1 0;
2(3+ 5+a) +a 0; 6+ 2 5+a +a 0; 5+a+ 2 5+a +1 0;
( 5+a +1)2 0.Даний вираз дійсний для любого значення a−5.
 Для
x2 = 3− 5 + a :
Для
x2 = 3− 5 + a :
![]()
![]() 2(3− 5+ a)+ a 0; 6−2 5+ a + a 0; 5+ a −2 5+ a +1 0;
2(3− 5+ a)+ a 0; 6−2 5+ a + a 0; 5+ a −2 5+ a +1 0;
( 5 + a −1)2 0.Даний вираз дійсний для любого значення a−5.
Значить перша умова ОДЗ ніяких обмежень на корені не дає.
![]() Перевіримо
другу умову ОДЗ. Для x1 = 3+ 5+a :
Перевіримо
другу умову ОДЗ. Для x1 = 3+ 5+a :
![]()
![]() 3+ 5+a −2 0; 1+ 5+a 0. Даний вираз
дійсний для любого значення a−5.
3+ 5+a −2 0; 1+ 5+a 0. Даний вираз
дійсний для любого значення a−5.
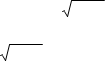 Для
x2 = 3− 5 + a :
Для
x2 = 3− 5 + a :
![]()
 3− 5 + a − 2 0; 1− 5+a 0; 1 5+ a; 1 5 + a; a−4.
3− 5 + a − 2 0; 1− 5+a 0; 1 5+ a; 1 5 + a; a−4.
Тобто для a(−4;+) корінь x2 = 3− 5+a не існує.
Проаналізувавши розв’язок отримуємо відповідь.
Якщо a(−;−5), то рівняння розв’язків не має.
![]() Якщо
a−5(−4;+), рівняння має
один розв’язок x =
3+ 5+ a.
Якщо
a−5(−4;+), рівняння має
один розв’язок x =
3+ 5+ a.
![]()
![]() Якщо
a(−5;−4,
рівняння має два розв’язки x1 =
3+ 5+ a; x2 = 3− 5+ a.
Якщо
a(−5;−4,
рівняння має два розв’язки x1 =
3+ 5+ a; x2 = 3− 5+ a.
2. Дослідження за допомогою програми GeoGebra.
а) на полотні розмістити повзунок a,a−10;10,h=0.05;
б) побудувати графіки функцій y = sqrt(2x + a) та y = x −2.
в) змінюючи значення параметра a за допомогою повзунка,
розглянути різні випадки розміщення графіків.
Якщо a(−;−5), то рівняння розв’язків не має.
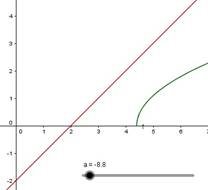
Рис. 5.1
![]() Якщо
a−5(−4;+), рівняння має один
розв’язок x = 3+ 5+ a.
Якщо
a−5(−4;+), рівняння має один
розв’язок x = 3+ 5+ a.

Рис. 5.2 Рис. 5.3
![]() Якщо
a(−5;−4,
рівняння має два розв’язки x1 =
3+ 5+ a; x2 =
Якщо
a(−5;−4,
рівняння має два розв’язки x1 =
3+ 5+ a; x2 = 3−
3−
Рис. 5.4
Відповідь: 1) Якщо a(−;−5), то рівняння розв’язків не має.
2)
![]() Якщо
a−5(−4;+), рівняння має один
розв’язок x = 3+ 5+ a.
Якщо
a−5(−4;+), рівняння має один
розв’язок x = 3+ 5+ a.
3)
![]()
![]() a(−5;−4,
рівняння має два розв’язки x1 =
3+ 5+a; x2 = 3− 5+a.
a(−5;−4,
рівняння має два розв’язки x1 =
3+ 5+a; x2 = 3− 5+a.
Висновки
Завдання з параметрами становлять хоч і невелику, але помітну частину математики. Матеріал, пов'язаний з рівняннями і нерівностями, що містять параметри, становить значну частину курсу. Це пояснюється тим, що рівняння і нерівності широко використовуються в різних розділах, при вирішенні важливих прикладних задач. Вивчення багатьох фізичних процесів і геометричних закономірностей часто призводить до вирішення завдань, що містять параметри. Сьогодні немає необхідності доводити актуальність теми «Завдання з параметрами» в рамках навчання математики. Також завдання з параметрами включені в завдання ЗНО. Вони часто бувають дуже складними і вимагають нестандартного підходу до вирішення.
На перших заняттях розв’язування завдань з параметрами, не потрібно примушувати студента розв'язувати задачі графічними методами. Необхідно дати йому можливість самостійного вибору методу вирішення тієї чи іншої задачі (функціонального або аналітичного). І тільки після цього, на прикладах в порівнянні з аналітичним або функціональним методами показати переваги графічного методу, того що використання цього методу в сукупності часто спрощує і скорочує час вирішення того чи іншого завдання з параметром.
GeoGebra це відмінний інструмент, який дозволить не просто урізноманітнити заняття з математики, а підвищити рівень якості розв’язування задач.
Використання програми GeoGebra на заняттях дозволяє: - оптимізувати навчальний процес, більш раціонально використовуючи час;
- здійснювати диференційований підхід в навчанні;
- проводити індивідуальну роботу, використовуючи персональні комп'ютери;
- розширювати кругозір студентів;
- сприяє розвитку пізнавальної активності студентів.
Прогнозовані ефекти від застосування даної технології:
- можливе підвищення інтересу до досліджуваного предмета;
- підвищення рівня самооцінки;
- розвиток навички самоконтролю;
- спонукання до відкриття і вивчення нового в сфері інформаційних технологій.
Список використаних джерел
1. Горошко Ю. В. Використання комп’ютерних програм для створення динамічних моделей при вивченні математики / Ю. В. Горошко, Є. Ф. Вінниченко // Науковий часопис НПУ імені М. П. Драгоманова. Серія №2. Комп’ютерно- орієнтовані системи навчання: зб. наук. праць / К. : НПУ імені М. П. Драгоманова, 2006. — № 4 (11). — С. 56–62.
2. Горошко Ю. В. Розв’язування задач з параметрами за допомогою програми «GRAN-1». / Горошко Ю. В., Вінниченко Є. Ф. // Математика в школі. — 2008. — № 7–
8(84).
3. Грамбовська Л. В. Комп’ютерні динамічні моделі як засіб дидактичного забезпечення процесу навчання геометрії в сучасній школі. / Грамбовська Л. В., Яковчук О. М. // Комп'ютер у школі та сім'ї. — 2010. — № 7. — С. 14–17.
4. Друшляк М. Г. Комп’ютерні інструменти програм динамічної математики і методичні проблеми їх використання / М. Г. Друшляк, О. В. Семенихіна/ / Інформаційні технології і засоби навчання, 2014, Том 42, №4.
5. Жалдак М. І. Комп’ютер на уроках математики: посібник для вчителів. / Жалдак М. І. — Видання 2-е, перероблене та доповнене. — К. : РННЦ «ДІНІТ», 2003. — 324 с.
6. Кушнір В. А. Розв’язування математичних задач інтегративного змісту засобами комп’ютерного моделювання. / Кушнір В. А., Ріжняк Р. Я. // Математика в школі. — 2009. — №10 (97).
7. Ракута В. М. Бібліотека комп’ютерних моделей, як необхідна складова сучасного навчального середовища. / Ракута В. М. // Наукові записки. — Вип. 98. – Серія : Педагогічні науки. — Кіровоград: РВВ КДПУ ім. В. Винниченка, 2011. — С. 246–249.
8. Ракута В. М. Програми для роботи з функціями та графіками. / Ракута В. М. // Комп'ютер у школі та сім'ї. — 2010. — № 7 (87). — С. 29–33.
9. Ракута В.М. Система динамічної математики GEOGEBRA як інноваційний засіб вивчення математики / В.М.Ракута // Інформаційні технології і засоби навчання. 2012. №4 (30)
10. Храповицкий И. С. Методические рекомендации по применению электронного учебного издания Geometer’s Sketchpad в учебном процессе общеобразовательных учреждений / Храповицкий И. С. – 2008. – 71 с.
11. CABRILOG. Innovative Maths Tools [Електронний ресурс]. – Режим доступу: http://www.cabri.com.
12. GeoGebra Wiki [Електронний ресурс]. – Режим доступу:
http://www.geogebra.org.
-
Гарно дякуємо, дуже гарний матеріл


про публікацію авторської розробки
Додати розробку
