«Використання технологій продуктивного навчання на уроках математики»

 

 

 

 

                              Зміст

І.Використання технологій продуктивного навчання на уроках математики

ІІ. Проектування сучасного уроку математики

1.Модуль  вивчення нового матеріалу

2.Модуль вступного контролю.

3.Модуль узагальнення та систематизації знань

4.Модуль контролю.

 

ІІІ .Система уроків з використанням технології продуктивного навчання.

    10 клас «Функції . їх властивості і графіки»

 Урок 1.Властивості функцій

 Урок 2. Побудова графіків функцій за допомогою геометричних 

                 перетворень.

 Урок 3. Обернена  функція

 Урок 4. Рівняння-наслідки та рівносильні перетворення рівнянь

Урок 5. Застосування властивостей функцій до розв’язування рівнянь

 Урок 6. Рівносильні перетворення нерівностей. Метод інтервалів

 Урок 7. Рівняння і нерівності, що містять знак модуля

 Урок 8. Контрольна робота  з теми «Функції, їх властивості і графіки»

 

ІV. Розробки уроків з геометрії. 10 клас.

Тема Паралельність у просторі

V. Література

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

ВИКОРИСТАННЯ ТЕХНОЛОГІЙ ПРОДУКТИВНОГО НАВЧАННЯ      НА УРОКАХ МАТЕМАТИКИ

   Середня освіта, яка сформувалась у середині XX сторіччя, передбачала трансляцію учням готової інформації з предмета, а не засвоєння реальної діяльності методами тієї чи іншої науки. Переважання репродуктивних методів в організації навчальної діяльності призводить до послаблення внутрішньої мотивації учнів, зниження їхнього творчого потенціалу.
На думку відомих російських учених В. Ледньова, Ю. Ді та А.Хуторського «вирішення даної проблеми можливе в переході від навчання «як передачі знань учню» до продуктивної освіти, коли накопичення знань учня відбувається в процесі створення ним власних освітніх продуктів-гіпотез, досліджень, творів, правил, живописних картин, комп’ютерних програм тощо. Особистісний освітній розвиток учня – його знань, почуттів, здібностей, досвіду в цьому разі відбувається одночасно із залученням його в наукові й культурно-історичні процеси, як їх повноправного учасника.
       Сьогодні в Україні йде активний процес станов­лення системи освіти, орієнтованої перш за все на особистість учня. Відбуваються зміни освіт­ньої парадигми. Педагогіка суб'єкт-суб'єктних відносин завойовує все більше прихильників, адже прогресивні освітні технології тією чи іншою мірою спрямовані на реалізацію цієї ідеї.   Концепція профільного навчання у старшій школі спрямована на виконання закону України «Про загальну середню освіту», постанову Кабі­нету Міністрів України від 16.11.2000 р. № 1717 «Про перехід загальноосвітніх навчальних закладів на новий зміст і структуру  навчання». Вона ґрунтується на основ­них положеннях Концепції загальної середньої освіти і спрямована на реалізацію Національ­ної доктрини розвитку освіти, затвердженої Указом Президента України від 17.04.2002 р. № 347/2000.

У названих документах закладено нові підходи до організації освіти в старшій школі, що має функціонувати як профільна. А для підвищення ефективності профільної освіти необхідно вико­ристовувати інтерактивні технології, зокрема технології продуктивного навчання. Позитив­ний результат досягається, якщо продуктивне навчання є системою, а не епізодом. До всього вищесказаного можна додати, що вчитель, як активна сторона у навчальному процесі, також повинен змінюватися, прогресувати.

                  Основні характеристики продуктивного навчання.

Актуалізація поняття продуктивного навчан­ня пов'язана з реформуванням освіти. Під­вищення ефективності профільного навчання можливе лише через впровадження інтерак­тивних технологій. У зв'язку з цим виник термін «продуктивне навчання», яке означає не новий вид навчання, а таке навчання, яке забезпечує найвищу продуктивність, найкра­щий результат, виконання учнями всіх вимог до інформаційної і практичної компетентності з предмета, що викладено в розділі навчаль­них програм: «Учень повинен мати...» і «Учень повинен уміти...».

Перехід до продуктивної освіти можливий тоді, коли нагромадження знань в учня відбувається в процесі створення ним власних освітніх про­дуктів — гіпотез, досліджень, творів, правил, живописних картин, комп'ютерних програм тощо. Особистий освітній розвиток учня — його знань, почуттів, здібностей, досвіду — у цьому разі відбувається одночасно із залученням його до наукового і культурно-історичного процесу як повноправного учасника.

Наукові дослідження показали, що навчання може не тільки сприяти просуванню вперед, але й уповільнювати розвиток особистості. Якщо навчання ґрунтується не на усвідомленні й осмисленні, а переважно на запам'ятовуванні, то воно може на певному етапі гальмувати розвиток учня. Саме тому сьогодні першочер­говим є не здобуття суми знань, а розвиток особистості.

Ось чому велику увагу приділено такому виду навчання, як продуктивне, що створює умови для розумової діяльності дитини.

У рамках модернізації освіти зростає потре­ба в збільшенні питомої ваги продуктивного навчання в навчально-виховному процесі.

Про­дуктивне навчання — це процес освіти, метою якого є розвиток особистості в співтоваристві, а також удосконалення самого співтовариства. Цей процес спрямований на успішність у діяль­ності, орієнтований на продукт та осмислен­ня цієї діяльності в групі учнів за підтримки педагогів. «Продуктивне навчання спрямоване на набуття життєвих умінь, що іні­ціюють особисте зростання та індивідуальний розвиток, міжособистісне спілкування та вза­ємодію, а також самовизначення його учасни­ків. Як освітній процес продуктивне навчання реалізується в рамках індивідуального шляху, що являє собою послідовність кроків, де кожен крок має певний результат, оскільки є продук­тивно орієнтованою діяльністю в реальній жит­тєвій ситуації».

І. Підласий (Продуктивна педагогіка. — М. : Народное образование, 2003) визначає продук­тивне навчання таким чином: «Продуктив­ні — це необхідні, дієві, міцні, постійно акту­альні, сформовані на належному рівні знання та вміння». Це означення певною мірою збіга­ється з вимогами компетентнісного підходу до навчання.

Термін «продуктивне навчання» відбиває прин­ципову ідею активної, самостійної навчальної діяльності учня.

Продуктивність передбачає забезпечення чіт­кої спрямованості на реальний, конкретний кінцевий продукт, створений учнем у рамках навчально-пізнавальної діяльності під час опа­нування предмета.

Досвід багатьох країн, що входять до мере­жі продуктивних шкіл, доводить, що освіту можна було б переорієнтувати з трансляції знань і контролю їх формального засвоєння на організацію мотивованого, самостійного прак­тично орієнтованого навчання, результати якого подаються в конкретному соціально значимому продукті.

Продуктивне навчання відрізняється від відо­мих методів і форм навчання тим, що до проце­су навчально-пізнавальної діяльності додаються завдання, що потребують від учнів створення власного значимого продукту на підставі знань, якими вони володіють.

Між питанням як методом перевірки знань у традиційній системі навчання і навчальним завданням продуктивного навчання існує знач­на відмінність. Суть її в тому, що питання припускає відповідь, яку можна знайти, звер­таючись до тексту вже відомого знання (хто? що? коли? навіщо?). Виконання завдання несе в собі алгоритм самостійного пошуку інформації на основі трансформації, перенесення засвоєних знань і вмінь для розв'язання певних проблем, ситуацій тощо.

Навчальне завдання може створювати навчаль­ну ситуацію тоді, коли необхідно знайти від­повідь, а засобів для цього не завжди достат­ньо. Ситуація припускає знаходження способу дії, а не зміну предмета, з яким діє суб'єкт навчання.

Таким чином, систематична, з уроку в урок, організація пізнавальної діяльності учнів на основі таких завдань формує в них активну позицію. Тим самим продуктивне навчання створює умови для діяльнісного підходу до навчання й формування в учнів умінь утвер­джувати себе через постійну продуктивну діяльність.

Методологія продуктивного навчання передбачає:

1. збільшення важливості кожного учасни­ка у формуванні, реалізації та оцінюванні її (його) навчальної ініціативи у співпраці з іншими учасниками;
2. тісні зв'язки «шкільного заходу», «шкіль­ного співтовариства» і «шкільного реаль­ного життя»", у яких можна простежити відкриту й гнучку систему продуктивного навчання;
3. зміну ролі педагога, який стає наставником-співробітником;
4. створення відповідного освітнього середови­ща, зокрема доступу до нових інформацій­них технологій.

Продуктивне навчання як педагогічний метод відрізняється від спрощеного навчання тим, що в його основі лежить системне досвідчене вироб­ництво та рефлексія. Таке навчання здійсню­ють у ситуаціях практичної участі школярів за допомогою педагогів, які послідовно формують продуктивне навчання з урахуванням його кри­теріїв (особистісного, діяльнісного, соціального, культурного, технічного).

Мета та форми продуктивного навчання

Продуктивне навчання спрямоване на організа­цію навчальних занять, які сприяють створен­ню під керівництвом учителя проблемних ситу­ацій, й активну самостійну діяльність учнів з їх розв'язання, у результаті чого відбувається роз­виток розумових здібностей особистості та твор­че оволодіння знаннями, навичками, уміннями. Пізнавальна самостійність учнів у навчанні визнається й визначається як готовність особис­тості до оволодіння знаннями власними силами. А пізнавальна активність полягає в тому, що учень, аналізуючи, порівнюючи, синтезуючи, узагальнюючи та конкретизуючи фактичний матеріал, сам шукає та одержує нову інфор­мацію. Розумовий процес — складний процес, який, як правило, починається з виникнення проблеми. Але не всякий пошук пов'язаний із виникненням проблеми. Якщо вчитель дає завдання, указавши, як його виконати, то навіть самостійний пошук не буде розв'язанням проблеми.

Постановка практичних завдань як практично орієнтованого змісту освіти докорінно змінює всю справу навчання. Самовизначення стиму­лює мотивацію.

Освітні цілі в продуктивному навчанні — отри­мання конкретного продукту в результаті само­стійної предметної діяльності учня згідно із загальними вимогами навчання.

Головні переваги продуктивного навчання:

У продуктивному навчанні важливу роль віді­грає групове навчання. Навчання в групі ефек­тивне тим, що відповідає високим педагогічним завданням продуктивного навчання: впевненості кожного у власних силах та засвоєнню «клю­чових характеристик», що надзвичайно важ­ливі в самовизначенні та відчутті успішності. З цієї причини комутативні якості дуже цінні: з'являється усвідомлення себе та інших, сприй­нятливість до нової інформації та нового досві­ду, здатність діяти відповідно до них, а також відповідно до навичок виражати свої почуття та думки і, нарешті, здатність співпрацювати з іншими.

   Технологія продуктивного навчання надає можливість навчати  на основі практичного життєвого досвіду, що допомагає молоді в їхньому професійному пошуку, розв’язанні їхніх соціальних, освітніх психологічних і культурних проблем.
   Продуктивне навчання – це процес освіти, метою якого є розвиток особистості в співтоваристві, також удосконалення самого товариства. Цей процес спрямований на успішність у діяльності, орієнтований на продукт, та осмислення цієї діяльності в групі учнів за підтримки педагогів.
    Продуктивне навчання спрямоване на набуття життєвих умінь, що ініціюють особистісне зростання та індивідуальний розвиток, міжособистісне спілкування та взаємодію, а також самовизначення його учасників.
    Продуктивне навчання – продуктивно орієнтована діяльність в реальній життєвій ситуації учнів.
    Продуктивне навчання – це навчання, що забезпечує реальний зв’язок освіти з життям, відкриває перспективу молодим людям за допомогою своїх знань і вмінь знайти роботу, домогтися успіху у житті.
     Продуктивне навчання – це процес створення учнями певного продукту, процес набуття життєвих навичок, які забезпечують самовизначення та особистісний розвиток кожного учня.
Продуктивне навчання – орієнтація педагогічної діяльності на одержання навчального і предметного продукту в самостійній діяльності.
 

Проектування  сучасного уроку математики

                                                                                Урок — це дзеркало загальної і

                                                                               педагогічної  культури вчителя,

                                                                             мірило його інтелектуального

                                                                           багатства, показник його

                                                                         світогляду, ерудиції.

В. Сухомлинський

Життя вимагає від особистості самостійного й відповідального пошуку його сенсу через індивідуальні способи існування, і освіта в цьому плані відіграє досить важливу роль. Яка  освіта сьогодні вважається якісною?

 Сьогодні ми все частіше визначаємо , що навчальний процес не є процесом підготовки школяра до життя, він не є «додатком» до нього -  теорія освітнього процесу повинна відбивати теорію життя, тільки за таких умов освіта стає якісною.

Продовжуючи працювати так , як працювали раніше, ми не  в змозі достатньо якісно виконувати головне завдання освіти - давати таку освіту, яка б дозволяла випускнику адекватно, природно сприймати дійсність, не виживати в суспільстві. А жити гідним життям, реалізовувати свої здібності. Сьогодні важливим стає не стільки  те, що випускник знає і навіть вміє застосовувати в лабораторних умовах, а те. Як він володіє прийомами пізнання світу. Здібностями і вміннями здобувати нові  знання та використовувати їх як засіб існування в суспільстві. 

   Однозначних поглядів на підготовку вчителя до уроку досі немає. Проте всі вважають , що підготовка сучасного уроку - складна і відповідальна справа.

В.О.Сухомлинський одним  із перших у новій педагогіці відчув необхідність перебудови підготовки уроку для успішного вирішення завдань, що постійно зростають. Він залишив цінні поради вчителям, у яких розкриваються важливі нюанси підготовчої діяльності.

 Основною формою організації навчально-виховного процесу  був і  залишається  урок.

Як учитель-практик розумію, що проведення якіс­ного, ефективного уроку (тобто такого, що досягає своєї мети) є провідним завданням педагога, основ­ною складовою його діяльності. Як же на практиці реалізувати це складне завдання?

 

Перш за все, це ефективне проектування уроку.

Під педагогічним проектуванням уроку розумію розробку системи взаємодії вчителя та учнів, що включає зміст, форми, методи та засоби навчання і виховання в процесі навчання, які дозволяють до­сягти певної чітко сформульованої мети навчаль­но-виховного процесу.

Переконана, що сучасний урок вимагає від учителя такого проектування, яке забезпечить за помірних витрат часу і зусиль педагога забезпечувалася найвища якість підготовки. Продуктивний урок –це урок добре підготовлений і майстерно проведений.

Так, під час підготовки до уроку треба враховувати сучасні вимоги:

•   загальнопедагогічні,
•   дидактичні,
•   психологічні,
•   валеологічні,

що дозволяють забезпечити ефективне проведення уроку.

У процесі практичної діяльності увесь навчальний матеріал  розподіляється  в модулі відповідно до типів, структури, вимог підготовки та організації сучасного уроку, змісту і техніки його проведення. Модуль це складова методики вчителя, у проектуванні уроку, організації всіх видів діяльності, яку необхідно забезпечити для по­вноцінного засвоєння матеріалу та його практично­го застосування, спрямовану на формування та роз­виток ключових (загальних і навчальних) компетен­тностей особистості.

Кожен модуль містить у собі мету, методи, прийо­ми, форми навчання, засоби, якими слід користуватися під час підготовки (проектування) уроку з конкретної теми.

 

 

		Створення умовної моделі уроку: • чітке визначення місця уроку і в змістовому, і в методичному аспекті в межах навчального курсу, розділу, теми; • формулювання загальної мети вивчення матеріалу; • відбір педагогічних методів, прийомів, технологій, використання яких забезпечить досягнення поставленої мети найбільш раціо­нальним шляхом
Моделювання

 

		Створення структури педагогічного процесу: • визначення виховних і розвивальних завдань; • прогнозування результатів; • опрацювання змістової частини матеріалу; • визначення методів, прийомів роботи; • прогнозування навчальних та загальних компетентностей, які фор­муватимуться на уроці
Проектування

 

		Створення конструктора (конспекту) уроку: • чітке формулювання мети, завдань, типу, форми проведення уроку; • конкретизація методів, прийомів; • запис дій учителя та передбачення дій учнів; • раціональний розподіл часу; • виділення структурних елементів навчальної діяльності
Конструювання

 

 

 

 

Проектування конкретного уроку здійснюється трьома послідовними етапами:

На уроках визначаю такі модулі: модуль психологіч­ного супроводу, модуль вступного повторення, мо­дуль вивчення нового матеріалу, модуль практики, модуль спостереження, діагностики, модуль домаш­ньої роботи, модуль узагальнення та систематизації вивчених знань, модуль контролю, модуль корекції.

Модуль психологічного супроводу

Мета:

1. Врахувати психофізіологічні особливості учнів.
2. Розвивати пізнавальні процеси (пам'ять, увагу, сприймання, мислення, мовлення, уяву тощо) та математичні здібності учнів.
3. Формувати якості особистості учня та пізнаваль­ний інтерес.
4. Створити позитивно-емоційний настрій і психо­логічно комфортні умови.
5. Сприяти позитивному відношенню учнів до на­вчання.

Методи: інтерактивні, ігрові, релаксаційні тощо.

 

Прийоми: «Світлофор настрою», «Навіювання», «Відстрочена відгадка», «Бліцопитування», «Снігова куля», «Релаксаційні вправи», «Зворотний зв'язок» тощо.

Форми навчання: індивідуальні, парні, групові, фронтальні, колективні.

Засоби: ТЗН, інформаційні таблички тощо.

Модуль вступного повторення

Мета:

1. Визначити рівень попередньої підготовленості учнів, що стосується теми.
2. Актуалізувати знання, що потрібні для введення нового матеріалу.
3. Активізувати мислення учнів.
4. Формувати групи компетентностей: ціннісно-смислові, загальнокультурні, навчально-пізна­вальні, комунікативні.

Методи: фронтальна бесіда, усне опитування, робо­та зі схемами, рисунками, метод прогнозування, ро­бота з текстом підручника, самоперевірка за зраз­ком тощо.

 

Прийоми: «Інтрига», «Дивуй!», «Фантастична добав­ка», «Відстрочена загадка», заповнення кросвордів, «Альтернатива», «Світлофор», «Мозковий штурм», «Асоціація», «Зайве слово», «Назви відповідність», «Пошук загального», «Групування слів», «Матема­тичне лото», «Зашифровки», «Незакінчені речення» тощо.

Форми навчання: групова, парна, індивідуальна, фронтальна тощо.

Засоби: диктанти, тести, ТЗН, навчальні та наочні посібники, підручник, таблиці, моделі тощо.

Модуль вивчення нового матеріалу (презентації)

Мета:

1. Збільшити дидактичні одиниці.
2. Допомогти учням засвоїти факти та основні ідеї.
3. Забезпечити якість вивчення нового матеріалу.

5. Забезпечити диференційований підхід.

6. Встановити зв'язки між засвоєними та новими знаннями.
7. Формувати групи компетентностей: соціальні, інформаційні, комунікативні, навчально-пізна­вальні, особистісного самовдосконалення.

Методи: пояснення, коментоване читання тексту підручника, лекція-інформація, лекція-консульта-1 ція, проблемна лекція, оглядова лекція, семінар-практикум, фронтальна бесіда, дискусія, робота з книгою, посібниками, схемами, таблицями, ри­сунками, моделями, демонстрація презентацій.

Прийоми: «Асоціації», «Мозкова атака», створення проблемної ситуації, використання яскравих афо­ризмів, порівнянь, образів, «Знаємо — бажаємо дізнатися — дізналися», «Моделі, що ожили», «Сні­гова грудка», «Ажурна пилка», «Акваріум», «Броунівський рух», «Два-чотири — всі разом», «Навчаючи — учусь», «Павучки», «Місткий кошик» тощо.

Форми навчання: парна, групова, індивідуальна, ко­лективна, фронтальна.

Засоби: ТЗН, підручники, посібники, довідники,інформаційні таблички, роздавальний ма­теріал, таблиці, моделі тощо.

Прийоми: «Інтрига», «Дивуй!», «Фантастична добав­ка», «Відстрочена загадка», заповнення кросвордів, «Альтернатива», «Світлофор», «Мозковий штурм», «Асоціація», «Зайве слово», «Назви відповідність», «Пошук загального», «Групування слів», «Матема­тичне лото», «Зашифровки», «Незакінчені речення» тощо.

Форми навчання: групова, парна, індивідуальна, фронтальна тощо.

Засоби: диктанти, тести, ТЗН, навчальні та наочні посібники, підручник, таблиці, моделі тощо.

Мета:

Модуль практичного застосування знань

1. Формувати вміння практичного застосування знань, умінь і навичок.
2. Формувати й удосконалювати вміння і навички у стандартах прямого й успішного руху до накре­сленої мети.
3. Забезпечити ситуацію вибору.
4. Формувати вміння розв'язувати типові задачі, формувати творчі вміння.
5. Переносити знання і способи діяльності, жит­тєвого досвіду в нову ситуацію.
6. Формувати групи компетентностей: комуніка­тивні, інформаційні, саморозвитку і самоосвіти, продуктивної творчості, вміння вчитися.

Методи: практичні роботи, розв'язування задач за зразком, метод коментування, робота з підручником та різними джерелами інформації.

Прийоми: «Класифікація», «Альтернатива», «Синтез думок», математичні змагання, «Коментування», «Навчаючи - учусь», «Асоціативний ряд», «Кару­сель», «Поєдинок», «Інтелектуальний тир» тощо.

Форми навчання: парна, групова, індивідуальна, ко­лективна, фронтальна.

Засоби: роздавальний матеріал, математичні дик­танти, тести, ТЗН, схеми, навчальні та наочні по­сібники.

Модуль спостереження, діагностики

Мета:

1. Організувати і підтримати безперервний зворот­ний зв'язок.
2. Одержати своєчасну інформацію про успішність просування у навчанні всіх учнів.
3. Спостерігати за процесом засвоєння та застосу­вання знань, умінь, навичок.
4. Здійснювати моніторинг навчальних досягнень учнів.
5. Формувати на кожного учня «досьє» (залучаючи комп'ютер), до якого тільки він та вчитель мають доступ.
6. Формувати групи компетентностей: соціальні, ціннісні, комунікативні, культурні.

 

Методи: спостереження, дискусія, створення про­блемної ситуації.

Прийоми: рефлексія, «Світлофор настрою», «Релак­саційні вправи», «Зворотний зв'язок» тощо.

Форми навчання: індивідуальна, парна, колективна, . фронтальна.

Засоби: завдання для моніторингу рівня знань, ком­п'ютер, навчальні та наочні посібники, ТЗН.

Модуль домашньої роботи

Мета:

1. Удосконалити, узагальнити, систематизувати знан­ня, вміння та навички.
2. Розвивати самостійність та творче мислення.
3. Формувати вміння самостійно засвоювати ок­ремі питання навчального матеріалу.
4. Формувати групи компетентностей: інформацій­ні, саморозвитку і самоосвіти, продуктивної творчості, вміння вчитися.

Методи: виконання вправ, письмових і графічних робіт, підготовка рефератів, доповідей, самопере­вірка, індивідуальне опитування, фронтальна бесі­да, робота з підручником, довідниками, додатковою літературою, використання Іпіегпеї.

Прийоми: «Інтелектуальна розминка», «Вірю — не вірю», «Так — ні»; бліцопитування ланцюжком, «Знайди помилку», «Світлофор», «Творче завдан­ня», «Заздалегідь», «Одне завдання на двох», «Вибе­ри сам», «Ярмарок-продаж» тощо.

Форми навчання: індивідуальна, парна, групова.

Засоби: навчальні та наочні посібники, довідкова література, інформаційні таблички, Іпіегпеї тощо.

Модуль узагальнення та систематизації набутих знань

Мета:

1. Узагальнити та систематизувати знання, вміння й навички.
2. Установити загальні зв'язки в матеріалі, що доз­воляє учням побачити тему (розділ) у цілому.
3. Формувати вміння застосувати набуті знання під час розв'язування задач різного рівня складності.
4. Формувати потреби до постійної самоосвіти.

Методи: порівняння, узагальнення, усна розповідь, бесіда, вступні, оглядові, самоорганізуючі, пошу­кові семінари, індивідуальні та групові семінари, семінари з розв'язування задач, дебати, конфе­ренції.

Прийоми: «Письмовий звіт», «Шпаргалка», «Пош­та», «Перепишу параграф по-своєму», «Я — вчи­тель», «Інтелектуальне лото», рефлексія, «Ділова гра», «Аукціон Ідей», «Творча робота», «Учені та їхні відкриття», «Фантастичні фі гури» тощо.

Форми навчання: індивідуальна, парна, групова, ко­лективна, індивідуально-колективна, фронтальна.

Засоби: тести, інформаційні картки, навчальні та наочні посібники, ТЗН тощо.

                              Модуль контролю

Мета:

1. Визначити рівень навчальних досягнень учнів відповідно до вмінь самостійно здобувати, аналі­зувати, систематизувати і творчо застосовувати отриману інформацію, приймати рішення та ар­гументувати власну думку.
2. Поєднати перевірку знань із повторенням і за­кріпленням навчального матеріалу та визначити рівень навчальних досягнень учнів.
3. Активізувати навчально-пізнавальну діяльність учнів усього класу.
4. Здійснити диференційований контроль.
5. Формувати групи компетентностей: саморозвит­ку та самоосвіти, продуктивної творчості, осо­бистого самовдосконалення, вміння вчитися.

Методи: усне опитування, контрольні та залікові семінари, письмові контрольні та самостійні робо­ти, контроль із використанням комп'ютера, пере­вірні-роботи, заліки, самоперевірка за зразком, за алгоритмом.

Прийоми: «Математичні змагання», «Інтелектуальна розминка», «Спринт-робота» тощо.

Форми навчання: індивідуальна, парна, групова.

Засоби: тести, різнорівневі завдання, математичні диктанти, ТЗН тощо.

                     Модуль корекції

Мета:

1. Формувати вміння аналізувати та осмислювати помилку, необхідність її усунення, шляхи досяг­нення позитивного результату.
2. Здійснити диференційований підхід, враховуючи індивідуальні особливості учнів.
3. Забезпечити індивідуальний набір завдань із ура­хуванням різних рівнів навченості учнів.
4. Формувати групи компетентностей: комуні­кативні, саморозвитку і самоосвіти, навчально-пізнавальні.   .

Методи: письмові роботи, тестування, робота зі схе­мами, таблицями, з конкретними завданнями, ро­бота з підручником, із завданнями для корекції знань, консультації, робота за зразком, коментована робота, робота за алгоритмом, схемою.

Прийоми: «М'яч зі словами», «Приваблива мета», «Спіймай помилку», «Шпаргалки» тощо.

Форми навчання: індивідуальна, групова, парна, фронтальна, колективна.

Засоби: навчальні та наочні посібники, завдання для корекції знань, ТЗН.

Під час проектування уроку використовуються різні модулі відповідно до поставленої мети, типу уроку та його структури.

Обов'язковим елементом роботи над проектуван­ням уроку є корекція після проведення уроку, визначення нових траєкторій руху вчителя і учня на уроці. Це дає можливість у майбутньому провести урок із цієї теми більш ефективно, сприяє набуттю досвіду в проектуванні інших уроків.

Саме тому проектування уроку є однією з найваж­ливіших функцій учителя, складає значну часову й змістовну частину педагогічної діяльності, потре­бує продуманої, спланованої, систематичної робо­ти. Педагогічне проектування в цілому сприяє по­стійному самоаналізу діяльності вчителя, його твор­чому й професійному зростанню

         

                МОДУЛЬ    ВИВЧЕННЯ  НОВОГО МАТЕРІАЛУ

                      Добірка схем, памяток, алгоритмів.

                         ЯК СКЛАСТИ КОНСПЕКТ

-Прочитайте текст підручника .

-Запишіть у зошиті тему конспекту.

-Визначте в тексті головний зміст, основні ідеї, поняття, закономірності, формули тощо.

-Основний  зміст кожного значеннєвого компонента законспектуйте у вигляді кодованої інформації після запису теми в зошиті.

-Прочитайте ще раз текст і перевірте повноту записаних ідей.

-Сформулюйте не менш ніж три запитання  різного рівня складності, запишіть їх у зошит.

-До кожного запитання знайдіть позначку ступеня складності та можливу відповідь.

-Уважно прочитайте матеріал.

-Визначте основні частини навчальної інформації за планом загальної схеми.

ЯК ПОТРІБНО КОНСПЕКТУВАТИ

-Перед конспектуванням необхідно ретельно вивчити параграф, який будете конспектувати.

-Конспектуванню передує складання плану.

-Виклад тексту подавайте стисло, але основні думки й аргументи слід записувати докладно.

-У конспекті можна використовувати цитати.

- На початку конспекту необхідно точно вказати прізвище та ініціали автора, повну назву роботи, місце й рік створення.

ЯК ПРАЦЮВАТИ З КНИГОЮ

- Читайте книгу з олівцем у руці. Якщо книга власна , тоді охайно робіть позначки на полях у тих місцях, які зацікавили або викликали запитання.

- Намагайтеся читати швидко , але уважно.

- Прочитавши книгу, поміркуйте над її основними ідеями, над описаними в ній подіями, фактами.

- Зробіть запис про те, що здалося особливо важливим у прочитаній книзі, про її основні переваги й недоліки.

ЯК ЗАПАМ’ЯТОВУВАТИ  ОЗНАЧЕННЯ ПОНЯТЬ , ТЕРМІНІВ, ЗАКОНОМІРНОСТЕЙ

Прочитайте означення в підручнику, а потім у робочому зошиті.

Визначте змістове значення поняття.

Підкресліть ключові слова.

Прочитайте записане й проговоріть уголос.

Зобразіть поняття умовними позначками, схемою тощо.

Прочитайте написане.  Повторіть двічі весь цикл.

ЯК РОЗВ’ЯЗАТИ ЗАДАЧУ

- Уважно прочитайте текст задачі, намагаючись  зрозуміти її суть.

- Проаналізуйте задачу.

- Запишіть умову задачі , використовуючи загальноприйняті позначення (скорочений запис)

- Підберіть найбільш раціональний спосіб розв’язування .

- Виконайте математичні обчислення.

- Запишіть відповідь.

- Виконайте перевірку (аналіз) розв’язання.

  СТРУКТУРА ПРОЦЕСУ РОЗВ’ЯЗАННЯ   ЗАДАЧІ

1.Аналіз задачі.

2.Схематичний запис умови задачі.

3.Пошук способу розв’язання задачі.

4.Здійснення розв’язання задачі.

5. Перевірка розв’язків задачі.

6.Дослідження задачі.

7.Формулювання відповіді задачі.

РЕКОМЕНДАЦІЇ ДЛЯ ПОШУКУ РОЗВ’ЯЗАННЯ         

                               ЗАДАЧІ

1.Прочитавши задачу, встановіть , до якого типу задач вона належить.

2. Якщо впізнали в ній стандартну задачу, то використайте для її розв’язування відоме вам правило.

3. Якщо задача не є  стандартною, то слід діяти наступним чином.

а)відокремте із задачі або поділіть її на під задачі стандартного виду;

б) уведіть в умову допоміжні елементи: допоміжні параметри, допоміжні умови;

в)переформулюйте її, замініть іншою рівносильною задачею.

3. Для того, щоб легше було розв’язати задачу виконайте її схематичний запис.

 

 

 

 

 

 

 

 

МОДУЛЬ ВСТУПНОГО КОНТРОЛЮ.

 

Тема. «Функції». 10 клас

Математичний диктант

 Закінчіть речення.

1. Область визначення функції – це…

2. Область значень функції –це…

3. Областю визначення функції f(x)= є…

4. Областю визначення функції f(x)=х³ +2х² +1 є…

 

5.Областю визначення функції у= є…

6. Знайдіть у(2), якщо у=

7.Чи належить графіку функції у= точка А(-3;0)?

8. У якій точці графік функції у=-х+8 перетинає вісь ординат?

9.Скільки точок перетину мають графіки у=|х| і у=-2?

10.Побудуйте графіки функції у=-х² -4, у=-3х-6.

 

Тема. Властивості функцій. 10 клас

Математичний диктант

 

1.Знайдіть нулі функції у=х²-7х +10.

2.Зростаючою чи спадною є функція у=7х+3?

3.Знайдіть проміжки знакосталості функції у=-х+1.

4.Функція у=f(x) зростає. Порівняйте f(4) і f(6).

5.Функція у=f(x) спадає. Порівняйте f(3) і f(7).

6. Знайдіть найбільше або найменше значення функції у=х²-6х +5.

7.Чи є дана функція оберненою на множині R?

                у=х³

8.Парною чи непарною є функція у= ?

 

9.Парною чи непарною є функція у=х² -6х +5?

10. Побудуйте графік функції у= (х+1)³.

11.Функція у =f(x) спадає. Порівняйте f(3) і f(7).

 

 

МОДУЛЬ УЗАГАЛЬНЕННЯ ТА СИСТЕМАТИЗАЦІЇ ЗНАНЬ

Добірка матеріалів за темою «Числові  функції, їх властивості та графіки»

                              10 клас

         КОНТРОЛЬНІ ЗАПИТАННЯ

 

1. Що називається функцією?

2.Як називають змінні х і у?

3.Як позначають функції?

4.Що називається значенням функції в точці х₀?

5.Що називається областю визначення функції?

6. Що називається областю значень функції?.

7.Способи задання функції.

8.Яка функція називається зростаючою ? Навести приклади.

9. Яка функція називається спадною ? Навести приклади.

10. Яка функція називається парною ? Навести приклади.

11. Яка функція називається непарною ? Навести приклади.

12.Як дослідити функцію на парність, непарність?

13.Які властивості графіків парної і непарної функцій  вам відомі?

14.Види функцій, їх графіки.

                ДОВІДКОВИЙ МАТЕРІАЛ

1.Залежність  змінної у від змінної х називається функцією. Якщо кожному значенню х відповідає єдине значення у.

2. Множина значень , які може приймати аргумент х, називається областю визначення функції.

3 Множина значень залежної змінної, які вона приймає при всіх значеннях області визначення функції.

4.Функція називається зростаючою, якщо більшому значенню аргументу відповідає більше значення функції.

5. Функція називається спадною, якщо більшому значенню аргументу відповідає менше значення функції.

6.Графік парної  функції симетричний відносно осі Оу.

7. Графік непарної функції симетричний відносно початку координат.

                 ЗАДАЧІ З РОЗВ’ЯЗАННЯМ

1.Знайти область визначення функції:

у=; D(y): ; х є (-

2.Знайдіть множину значень функції: у=х² -6х +5.

Найменшого значення дана функція набуває при х₀ =6\2=34 у₀ = 9-18 +5= -9 +5=-4.

Е(у)=[-4;+).

3. Дослідити на парність   та непарність функції

у= х⁵ -3х.

D(f)=R;  f(-x) = (-х)⁵ -3 (-х)= -х⁵ +3х=-(х⁵ -3х)=- f(х). Отже f(-x) =- f(х).Отже, ця функція є непарною.

4.Доведіть, що на області визначення функція у=2х-4 є зростаючою.

Доведення .

Нехай х₂ > х_1, тоді х₂ - х₁ >0.Розглянемо різницю:

у(х₂) –у(х₁)=2 х₂ -4-(2х₁ -4)=2 х₂ -4-2 х₁ +4 =2(х₂ - х₁₎ >0.

Таким чином, у(х₂)> у(х₁).Отже. функція у=2х-4 зростає на множині R.

 

 

                        

 

        ДИДАКТИЧНИЙ МАТЕРІАЛ

 

1.Накресліть ескіз графіка функції f, якщо:

а)функція зростає на проміжку (-;-2] і спадає на проміжку [-2;+);

б)функція спадає на проміжку (-;-1] і зростає на проміжку [-1;+).

2.Доведіть, що функція:

f(x)=х⁴  + 3х зростає на [0; +).

3.Знайдіть область визначення функції:

а) f(x)=; б) ) f(x)=;

4.Задайте формулою яку- небудь функцію, областю визначення якої є:

- множина дійсних чисел, крім чисел 1 і 2;

-множина всіх чисел не менших від 5.

5.Побудуйте графік функції

    f(x)=;   f(x)=|х² -4|;     f(x)=||х|-4|; у=

6.Знайдіть функцію обернену до даної:

       у=3х-1 ; у=;   у=4х-5;   у=.

7.При яких значеннях а точка Р(4;4) належить графіку функції у=а?

 

                        МОДУЛЬ КОНТРОЛЮ

Контрольна робота з теми «Числові функції їх властивості і графіки»

Варіант 1

 Початковий та середній рівні навчальних досягнень

У завданнях 1-6 виберіть правильну відповідь.

1. Функцію задано формулою f(x)=.Знайдіть f(4).

а) ; б) ; в) ; г); д).

2.Знайдіть область визначення  f(x)=.

а)[0,5; +) б) (-; 2];  в)(-;0,5); г)(-0,5;+); д) (-; 0,5].

 

3.Яке з наведених чисел не входить до області визначення функції

f(x)=?

а) 1; б) 0; в) -3; г) -7.

4.Множиною значень якої з наведених функцій є проміжок (-;5]?

А) f(x)=х+5; б) f(x)=;в) f(x)=х² -5; г) f(x)=-х² +5.

5.Графік якої з наведених функцій симетричний відносно осі Оу?

А) у=х+1; б) у=х² +1; в) у=;  г) у=х² –х.

6.Яке з наведених рівнянь рівносильне рівнянню -1=0?

А) ; б) 3-х=0; в) х-3=0 ; г)

Достатній рівень навчальних досягнень

7.Укажіть , які геометричні перетворення графіка функції f(x)= необхідно виконати , щоб одержати графік функції f(x)=.Побудуйте цей графік.

8.Застосовуючи властивості функцій, розв’яжіть рівняння .

Високий рівень навчальних досягнень.

9. Розв’яжіть рівняння |2х-3|=х

    10. Знайдіть суму натуральних чисел. Що входять до області визначення   

     функції у=.

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Урок 1.

Тема. Властивості функцій.

Мета:  повторити,узагальнити й розширити знання властивостей функцій ;      

             формувати вміння досліджувати властивості функцій та

              використовувати одержані результати для побудови графіків

              функцій;

              розвивати логічне мислення, вміння аналізувати,порівнювати.

             заохочувати учнів знаходити свій спосіб роботи;

              виховувати вміння самостійно працювати з підручником.

Тип уроку:  комбінований

                                                  Через математичні знання,одержанні в школі  ,

                                                     лежить шлях до великих відкриттів.

                                                                     Маркушевич Б.В.               

                                           План

1.Організаційний етап.

Модуль психологічного супроводу.

Прийом «Система малюнків»

Учні сигналізують про свій емоційний стан за допомогою спеціальних піктограм. Урок  розпочинається з того, що кожен учень показує один із малюнків, що відповідає його настрою. Вчитель  має можливість скорегувати настрій 2-3 реченнями, налаштувати учнів на роботу.

 

ІІ.  Пропедевтична практика

Бліцопитування.

1Що називається функцією?

2.Як називають змінні х і у?

3.Як позначають функції?

4.Що називається значенням функції в точці х₀?

5.Що називається областю визначення функції?

6. Що називається областю значень функції?

2. Математичний диктант

1.Запишіть область визначення функції:

а) f(x)=ахⁿ + вх^n-1 +…+m                         (R)

б) у=                                                   (g(x))

в) у=                                                  (f(x))

 

2. Знайдіть значення функції в зазначених точках:

а) f(x) =2х-6 у точках 3; -0,5; 0.

б) f(x)=2х² -4 у точках 0;-1;1.

3.Знайдіть значення аргумента, при якому значення функції f(x)=10-2х дорівнює 2.

4.Знайдіть область визначення функції:

 А) f(x)=3х² +6х-4;   б) у=; в) у=.

Відповідь: 4.а) R; б) х Є (-;-4) (-4;4) (4;+); в) х Є (-;-2) [3;+).

 

    ІІІ. Орієнтація.

 На цьому уроці ми   починаємо вивчення функцій – найважливішої теми курсу «Алгебра і початки аналізу», що спирається на знання, отримані  під час вивчення математики в 5-6  класах і курсу алгебри в основній школі. У 10 класі  ви поглибите і систематизуєте уже отримані знання, познайомитесь з новими функціями – тригонометричними й степеневими.

   Функція є однією з основних змістових ліній  курсу алгебри в школі. Багато відомостей про функції ви  вже знаєте із курсу алгебри 7-9 класів. Тож на цьому уроці  ми пригадаємо основні означення, щоб надалі розширювати й поглиблювати знання про функції.

 ІV. Презентація

План узагальнення і розширення знань

1.Властивості функцій:

- нулі функції;

- проміжки знакосталості;

- проміжки зростання, спадання, сталості;

- парність, непарність;

- найбільше та найменше значення

2. «Поведінка» графіка  функції:

1) на проміжках знакосталості;

2) на проміжках зростання, спадання, сталості.

3.Особливості графіків парної та непарної функцій.

Даний матеріал учні опрацьовують методом «ПОМІЧ» працюючи в групах

І група -§ 5

ІІ група-§ 6 ст.39- 41

ІІІ група -§ 6 ст.42- 43

ІV група --§ 7 ст.48-50

Після опрацювання матеріалу кожна група презентує свою роботу.

V. Керована практика

Усно  № 75,100

Рівень «С» № 76,78,102                    рівень «А» № 82, №89,№93,104

 

VІ. Незалежна практика

Рівень «С» №107.108                                рівень «А №117,146

 

VІІ. Підсумок уроку

За мал.30. визначити нулі функції, проміжки знакосталості функції,проміжки зростання і проміжки спадання, найбільше і найменше значення  функції.

 

VІІІ Домашнє завдання.

Мерзляк А.Г .»Алгебра і початки аналізу»

Вивчити -§ 5-7

Рівень «С» №77,101

Рівень «А» №95,109,147

 

Урок 2

Тема .  Побудова графіків функцій за допомогою геометричних 

                 перетворень.

Мета: узагальнити та систематизувати знання учнів щодо побудови графіків 

             функцій за допомогою геометричних перетворень;

              виховувати культуру виконання малюнка;

             розвивати логічне мислення,  толерантність під час групової        

             діяльності.

Тип уроку : узагальнення та систематизація знань

Обладнання: персональні комп’ютери , мультимедійний проектор

                                                          До знань ведуть  три шляхи:

                                                          Шлях міркувань-цей шлях благородний;

                                                           Шлях наслідувань -він найлегший;

                                                           Шлях досвіду - він найважчий.

                                                                                              Конфуцій

                                        План

1.Організаційний етап.

Модуль психологічного супроводу.

Учні привітавшись з учителем сідають за парти назвавши математичне поняття із теми « Функція».

ІІ.  Пропедевтична практика

1.Наявність  письмового завдання перевіряють чергові  учні.

2 .Виконання усних вправ

1. Яка функція задається рівнянням 2х +5у =3 ? Який її кутовий коефіцієнт? Опишіть властивості цієї функції.
2. Під яким кутом перетинаються  графіки функцій у = х і у = - х?
3. Який  вигляд має графік функції у = х заданої на множині від’ємних чисел?
4. Доведіть, що функція у=3х +в, графік якої проходить через точку (-2;6), непарна.
5. Зростає чи спадає функція у = -кх -7 , якщо її графік проходить  через точку (2;6)?
6. Знайдіть множину значень функції у=х² -2х+3
7. Назвіть проміжки спадання і зростання цієї функції.
8. Дослідіть на парність  і непарність функцію у=

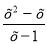
    Відповідь: ні парна ні непарна

ІІІ. Орієнтація.

Вчитель повідомляє тему і мету уроку. Звертає увагу учнів на те, що даний матеріал вивчався у 9 класі, і на цьому уроці учні систематизують і узагальнюють матеріал.

План вивчення теми

1.Перетворення графіків функцій

1) f(x) f(x +a) f(x – a);

2)  f(x) f(x )+b f(x ) -b;

3) f(x) k f(x );

4) f(x) f(nx ), n>0;

5) f(x) |f(x )|;

6) f(x) f( |x| ).

ІV. Презентація

 Учні об’єднуються в пари і готують презентацію  по побудові  графіків заданих функцій. Самостійна робота з підручником Мерзляк А.Г. «Алгебра і початки аналізу « 10 кл. §8  ст.53-58

І пара      f(x) f(x +a) f(x – a);

                f(x) f(x )+b f(x )-b;

ІІ пара    f(x) k f(x );

ІІІ пара    f(x) f(nx ),

ІV пара   f(x) |f(x )|;   V пара  f(x) f( |x| ).

Учні опрацьовуючи матеріал розглядають приклади, складають таблицю в  зошит.

Функція	Схематичне зображення графіка функції	Область визначення функції	Область значень функції

 

Вчитель може використати  мультимедійний проектор і показати учням заздалегідь підготовлену таблицю та графіки функцій.

V. Практика на прикладах.

Для побудови графіків функцій учні використовують персональні комп’ютери, програму GRAN 1 .

№168  рівень «С» 

№177 рівень «А»

Усно №170,№171 

Колективне виконання №173

VІ. Керована практика

№180.1,2, №185

Побудуйте графіки функцій:

 у=|x|;   у=|x-1|;   у=|x|-1;   у=|x-1|-1; рівень «С»

у= |x²-2х +3|;  у=х² -2|x| +3;    рівень «А»

  

VІІ. Підсумок уроку

Учитель відповідає на запитання учнів. Пов’язані з темою уроку, і пропонує скласти план побудови графіка функції у=-2(х+1)² -3.

Можлива відповідь

а) Будуємо графік функції у=х²;

б) розтягуємо його вдвічі від осі Ох;

в) відображаємо побудований графік симетрично відносно осі Ох;

г) переміщуємо отриманий графік уздовж осі Ох ліворуч на одну одиницю;

д) переміщуємо графік на три одиниці вниз уздовж осі Оу.

Домашнє завдання.

Мерзляк А.Г. §8  ст.53-58

Рівень «С» №175,174

Рівень «А» № 186,190

 

 

 

 

Урок 3

Тема. Обернена  функція

Мета: сформувати поняття оберненої функції, домогтися  розуміння того,

            яка функція може бути оборотною; сформувати вміння знаходити

             формулу функції, оберненої до даної;

              розвивати мислення , розумову активність, пізнавальну  

             самостійність.

Тип уроку:  засвоєння нових знань і вмінь

                                            

                                               У математичних питаннях не можна

                                              нехтувати    навіть найменшими помилками.

                                                                            І.Ньютон

 

 

                                       План

І.Організаційний момент

Модуль психологічного супроводу.

«Світлофор настрою»

У кожного учня сигнальна картка, один бік якої зелений, а другий – червоний.

Учитель просить учнів показати за допомогою світлофора , з яким настроєм вони прийшли сьогодні на урок.

    Я бажаю вам, щоб гарний настрій не залишав вас до кінця уроку. Якщо ж настрій не дуже вам подобається, намагайтеся працювати на уроці так, щоб він покращився.

  Видатний учений Ісаак Ньютон сказав: «У математичних питаннях не можна нехтувати  навіть найменшими помилками». Спробуйте знайти помилку у висловлюванні (запис на дошці).

Один громадянин писав про себе: «Пальців  у мене  двадцять п’ять на одній руці, стільки ж на другій, на ногах десять…» Чому він такий потворний?

(Після слова «двадцять» треба поставити дві крапки.)

 

ІІ. Пропедевтична практика.

(Перевірка домашнього завдання)

1.За заздалегідь виконаними на дошці  малюнками  учні перевіряють виконання домашнього завдання.

2.Індивідуальні завдання на картках

Побудувати графіки функцій:

Рівень «С»        у=х² +4

Рівень «А»       у=|х² -5х +6|

Коментар до побудови графіка»  у=|х² -5х +6|

а) Будуємо графік функції у= х² -5х +6;

б)частину графіка , що знаходиться під віссю Ох, симетрично відображаємо відносно осі абсцис4 дістанемо графік функції у=|х² -5х +6|

2.Тести

1) Які перетворення графіка функції у=х² необхідно виконати, щоб одержати графік функції у=х²-3?

А) перенести на 3 одиниці ліворуч ; б) перенести на 3 одиниці вгору;в) перенести на 3 одиниці праворуч; г) перенести на 3 одиниці вниз.

2) Які перетворення графіка функції у=х² необхідно виконати, щоб одержати графік функції у=х² + 8х +16?

А) перенести на 4 одиниці ліворуч ; б) перенести на 16 одиниць угору;в) перенести на 4 одиниці праворуч; г) перенести на 8 одиниць ліворуч і на 16 одиниць угору.

3) Графік якої з наведених функцій необхідно перенести на 2 одиниці вгору, щоб одержати графік функції у=?

а) у=2х; б) у= в) у=; г) у=.

3.Самостійна робота

1.Побудувати графіки функцій.

Рівень «А»:   а) у=|x+2|+1;    б) у==|x-2|-1;

 2.Накресліть ескіз графіка функцій у=f(х), яка спадає на проміжках

     (-; 1]; [4;+ ) і зростає на проміжках [1;4].

 

 1.Рівень  «С»  у=(х-2)²; у= х² +4; у=(х+ 3)² -1.

 2.Дослідіть функцію на парність у= х² -4х.

 

ІІІ. Орієнтація

 Відомо, що залежність шляху від часу руху тіла при його рівномірному русі з постійною швидкістю V₀ виражається формулою  S= V₀ t. Із цієї формули можна  знайти обернену залежність – часу від пройденого шляху t =. Функцію  t(s)= V₀ t.

Вчитель повідомляє тему і мету уроку.

План вивчення теми

1.Яка функція називається оборотною?

2.Означення функції . оберненої до поданої.

3.Властивості оберненої функції.

4.Графіки взаємно обернених функцій.

5.Знаходження формули функції. Оберненої до поданої

ІV. Презентація.

Завдання класу(по варіантах)

Із рівняння 2х-у-1=0 виразіть: 1) у через х; 2) х через у.

Отримали дві залежності:

1. у= 2х-1, де  у- залежна змінна, а х- аргумент;
2.  х=.

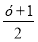Обидві залежності є лінійними. У наведеному прикладі функція х= є оберненою до функції у=2х-1, а у=2х-1-оберненою до функції х=.

Означення. Функція ,що приймає кожне своє значення в єдиній точці області визначення, називається оборотною.

Функція у=х² не є оборотною на всій області визначення. Проте на проміжку  [0;+ ) вона зростає і має  обернену у=.

 Завдання 1.Побудувати в одній системі координат графіки функцій у= 2х-1 та у = . Висновок роблять учні самостійно.

Алгоритм знаходження формули функції, оберненої до даної

1.Якщо функцію у=f(x) задано формулою. То для знаходження оберненої до неї функції треба розв’язати рівняння f(x)=у відносно х, а потім поміняти  місцями х і у.

2.Якщо рівняння f(x)=у має більше одного кореня, то функції. Оберненої до функції у=f(x), не існує.

3. Графіки даної та оберненої до неї функції симетричні відносно прямої у = х.                     (Робота з підручником. ст. 73)

4. Якщо функція у=f(x) зростає або спадає на певному проміжку , то вона оборотна.

5. Функція, обернена до  даної, визначена на області значень функції у=f(x) і також є зростаючою ( спадною)

V. Практика на прикладах.

1.Усно №217,

Робота в парах №220,

Колективно №222

VІ. Керована практика.

»С» - №224(1-4)

«А»-  226, 227(1-2)

VІІ. Незалежна практика

«С»

1.Знайдіть функцію, обернену до даної, і вкажіть її область визначення й множину значень.

у=х-5,     у=  ;       у=. х0

2.Побудуйте графіки даної та оберненої до неї функції в одній системі координат.

у=3х,    у=-2х +1

«А»

1.№229

VІІІ. Підсумок уроку

Закінчіть речення

1.Функцію називають оборотною, якщо…

2Якщо функція є зростаючою (спадною), то вона є …

3.Функція у=х² є …. на  множині [0;+ )  і ….на всій області визначення.

4.Графіки взаємно обернених функцій …

ІХ. Домашнє завдання.

Вивчити §10

«С»№ 221,223

«А» № 228,230

Додаткове завдання

Задайте  формулою функцію , обернену до функції у=, і побудуйте графіки поданої і оберненої до неї функцій.

 

 

 

Урок 4

Тема. Рівняння-наслідки та рівносильні перетворення рівнянь

Мета : сформувати поняття рівнянь-наслідків та рівносильних рівнянь;

            розвивати логічне мислення, вміння самостійно  працювати з            

             підручником; аналізувати виконану роботу та оцінювати її.

Тип уроку: узагальнення й систематизація знань.

 Девіз уроку:       Не кажи не вмію, а кажи навчусь.

                                       План

І.Організаційний етап

Модуль психологічного супроводу

Прийом «Система малюнків»

Учні сигналізують про свій емоційний стан за допомогою спеціальних піктограм. Урок  розпочинається з того, що кожен учень показує один із малюнків, що відповідає його настрою. Вчитель  має можливість скорегувати настрій 2-3 реченнями, налаштувати учнів на роботу.

ІІ. Пропедевтична практика.

(Перевірка домашнього завдання)

Бліцопитування

Встановіть відповідність між функцією f(x )і оберненою до неї функцією g(x)  .

Варіант 1                               

1	f(x)=2х +1	А	g(x)  =
2	f(x)=1 - 2х	Б	g(x)  =
3	f(x)=	В	g(x)  =
4	f(x)=	Г	g(x)  =

 

Варіант 2

1	f(x)=3х +1	А	g(x)  =
2	f(x)=-1 - 3х	Б	g(x) =
3	f(x)=	В	g(x)  =-
4	f(x)=	Г	g(x)  =

Відповіді: Варіант І  1-б. 2- в, 3-а. 4-г.

                  Варіант 2 1-г, 2-в, 3-б,4-г.

Вправа «Мікрофон»

1.Сформулюйте означення рівняння. Наведіть приклади лінійних, квадратних, дробово-раціональних рівнянь.

2.Що називається коренем рівняння?

3.Чи є число -2 розв’язком рівняння:

а) х² +4х +4=0; б) =0

4.Що означає розв’язати рівняння?

5. Чи можна  вважати розв’язаним рівняння х² –х-6=0, якщо вказано його корінь : х=3?

6. Що називається областю допустимих значень рівняння?

7.Знайдіть область допустимих значень рівняння:

а) =; б) =0; в) =.

8. Сформулюйте основні властивості рівнянь.

9.Чи є рівносильними такі рівняння?

а) 4х +5х=18 і 9х=18

б) х² +2х +2=0 і  х² +10х +26=0

в)( х+3) (х-3)=0 і |x|=3;  

 

ІІІ. Орієнтація

Вчитель повідомляє тему і мету уроку.

Оскільки учні уже знайомі з поняттям рівносильності  то можна даний матеріал вивчати використовуючи метод «ПОМІЧ».

План

1. Яке рівняння називається наслідком поданого рівняння?
2. Поява сторонніх коренів під час використання рівнянь –наслідків.
3. Означення рівносильних рівнянь.
4. Теорема про рівносильність рівнянь
5. Приклади рівнянь-наслідків і рівносильних рівнянь.

ІV. Презентація

 Оскільки учні уже знайомі з поняттям рівносильності  то можна даний матеріал вивчати використовуючи метод «ПОМІЧ».

Учні працюючи з підручником з’ясовують питання за планом .

Робота в парах.

1. На прикладах рівнянь показати  область їх визначення і знайти їх корені.
2.  Рівносильні рівняння. Приклади  таких рівнянь .
3. Перетворення які приводять до рівносильних рівнянь(Теореми 11.1-11.3)
4. Рівняння-наслідки. Приклади. Сторонні корені.

V. Практика на прикладах.

№237 (1-5)Усно

№239. Колективне розв’язання

VІ. Керована практика.

№240, №242 (1-4)

VІІ. Незалежна практика

«С» № 238 (1-4)

«А»  №242(5-8)

VІІІ . Підсумок уроку

 Запитання до класу

- Що таке ОДЗ рівняння?

- Дайте означення рівняння –наслідку даного рівняння.

- Дайте означення рівносильних на множині рівнянь

- Сформулюйте основні  твердження про рівносильність рівнянь

- Внаслідок яких перетворень даного рівняння можна одержати сторонні для даного рівняння корені?

Домашнє завдання

Вивч. §11

«А» № 243, 244

«С» № 238 (5-9),№ 239

 

 

Урок 5

Тема  уроку. Застосування властивостей функцій до розв’язування 

                                 рівнянь

Мета уроку: сформувати вміння застосовувати властивості функцій до 

                     розв’язування рівнянь; розвивати інтерес до математики,

                     пізнавальну активність; виховувати почуття колективізму.

Тип уроку: засвоєння нових знань і вмінь

                        

                                                              Розум полягає не тільки в знаннях , 

                                                              але й у вмінні застосовувати ці

                                                                знання.

                                                                                        Арістотель.

 

 ПЛАН

І.Організаційний етап.

Модуль психологічного супроводу.

Прийом «Барометр настрою»

Учитель  готує плакат із символами. Учні у відповідній колонці позначають точкою відповідь на запитання вчителя:

- Яким був твій настрій на початку  уроку?(і в кінці уроку)

ІІ. Пропедевтична практика

Рівень «С»

1.Чи рівносильні рівняння:

а) 7х-21=49 і х-3=7

б) =9 і 2х=27

в) х+5=х-1 і х(х-3)=х² +8-3х.

Рівень «А»

Розв’яжіть рівняння і виконайте перевірку.

1) + =;

2) + +=0

Відповідь : 1) х=4.    х=2-сторонній корінь

2) х=0,                         х=-2 сторонній корінь

2.Усні вправи

1.Розв’яжіть нерівність

а) 2х-18>0 ;  б) 3-2х0;  в) х² -16>0.

2)При яких значеннях змінної має зміст вираз:

А) ; б) в) ; г) .

3.Розв’яжіть систему нерівностей:

ІІІ.  Орієнтація.

 Під час розв’язування деяких рівнянь треба використовувати властивості функцій, оскільки стандартні методи або подовжують розв’язання, або взагалі не приводять до будь-якого результату.

Вчитель повідомляє тему і мету уроку, план вивчення теми.

- Яка функція називається зростаючою на даній множині?

- Що таке ОДЗ рівняння?

- За якої умови сума кількох невід’ємних чисел дорівнює нулю?

 

                                  План  вивчення теми

1.Способи розв’язання рівнянь із застосуванням властивостей функцій:

1) Використання скінченності області допустимих значень рівняння.

2) Оцінка правої та лівої частин рівняння.

3) Використання зростання та спадання функцій.

2.Приклади.

ІV. Презентація

- Яка функція називається зростаючою на даній множині?

- Що таке ОДЗ рівняння?

- За якої умови сума кількох невід’ємних чисел дорівнює нулю?

Вивчення нового матеріалу вчитель подає у формі опорного конспекту.

Орієнтир	Приклад
1.Скінченна ОДЗ
Якщо область  допустимих значень рівняння (нерівності або системи) складається із скінченного числа значень, то для розв’язування досить перевірити всі ці значення. Якщо ОДЗ- порожня множина (не містить жодного числа) –рівняння не має коренів. Приклад.=+5х	+х=1+ ОДЗ: х2=1,х=1,х=-1 Перевірка.+1=1+,  1=1 х=1-корінь х=-1 –не є коренем Відповідь: 1.
2.Оцінка лівої та правої частин	Рівняння
Якщо потрібно розв’язати рівняння виду f(x) =g(x) і з’ясувалося, що f(x)а, g(x), то рівність між лівою і правою частинами можлива лише у випадку , якщо одночасно f(x) і g(x 0 дорівнюють а. f(x)= g(x) f(x)= g(x) f(x)а, g(x),	1-х2 =.  f(x)=1-х2 1. g(x)= 1 ( бо 0. Отже , задане рівняння рівносильне системі х=0   Відповідь: 0.
f1(x)+f2(x) +…  + fn(x)=0 f1(x), f2(x)0,    fn(x) 0. Сума кількох невід’ємних функцій дорівнює нулю тоді і тільки тоді, коли всі функції одночасно дорівнюють нулю.	+ |х2 -2х| +(х2 -4)2=0. f1(x)= , f2(x)= |х2-2х| , f3(x)=(х2-4)2 0. Отже, задане рівняння рівносильне системі З першого рівняння одержуємо х=2, що задовольняє всій системі . Відповідь :   2
3. Використання зростання та спадання функцій	Теореми про корені рівняння
1.Підбираємо один або декілька коренів рівняння. 2.Доводимо , що інших коренів це рівняння не має(використовуючи теореми про корені рівняння або оцінку лівої та правої частин рівняння).	1.Якщо в рівнянні f(x)=а функція f(x) зростає (спадає) на деякому проміжку, то це рівняння може мати не більш ніж один корінь на цьому проміжку . Приклад. Рівняння +2х3 =3 має єдиний корінь х=1 ( +2 *1 =3, тобто  3=3). Оскільки функція f(x)=+2х3 зростає на всій області визначення х0. 2.Якщо  в рівнянні f(x)= g(x) функція f(x) зростає на деякому проміжку , а функція g(x) спадає на цьому самому проміжку(або навпаки), то це рівняння може мати не більш ніж один корінь на цьому проміжку . Приклад. Рівняння +х3 =3-х – має єдиний корінь х=1 , оскільки f(x)=+х3 зростає на всій області визначення х 0, а g(x)=3-х спадає (на множині R, а отже , і при х0).

V. Практика на прикладах.

1.Розв’язати рівняння

а)х³ +х=10       х=2

б)х³ +х=

ОДЗ: х0.Функція у= на всій області визначення не є ні спадною. Ні зростаючою, але вона  спадає на кожному з проміжків (-;0) і (0; +). Тому розглянемо кожен з цих проміжків окремо.

1. При х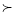0 задане рівняння має корінь х=1 ( 1+1=2, 2=2)
2.  При х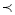0 задане рівняння має корінь х=-1(-2=-2)

      Функція у=х³ +х зростає при х0. а функція f(х)= спадає на цьому   

       проміжку.

Отже, задане рівняння   має тільки два корені: 1 і -1.

VІ . Керована практика.

1.Розв’яжіть рівняння х⁴ + =2-(х-1)².

Розв’язання.

ОДЗ:  х0.На ОДЗ х⁴ >0.Тоді функція f(x)= х⁴ + 2 (як сума  двох взаємно обернених додатних чисел), а функція  g(x)=2-(х-1)² 2.Отже, задане рівняння рівносильне системі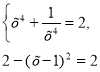

З другого рівняння  системи одержуємо х=1, що задовольняє і першому рівнянню. Отже ,  рівняння має єдиний розв’язок х =1.

2.Розв’яжіть рівняння використовуючи властивості відповідних функцій.

     +х² =+х+2.

Розв’язання.

 

ОДЗ:

ОДЗ складається з одного числа : х Є{2}.

Перевірка: правильно

Відповідь.х=2

VІІ .  Незалежна практика.

Розв’язати рівняння

Рівень “А»

а) 2х +;

Розв’язання.

 

 

ОДЗ: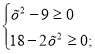

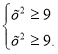
ОДЗ: х Є{-3;3}.

Перевіркою встановлюємо , що х=3 корінь рівняння

б) |х²-7х +12|+

Розв’язання.

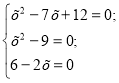х=3

Відповідь: х=3.

Рівень «С»

а) х² +х=0;

б)

в) х³ +х=2

VІІ. Підбиття підсумків уроку.

Користуючись складеною таблицею учитель разом з учнями повторює способи розв’язування рівнянь використовуючи властивості функцій

 Усно. Розв’язати рівняння

Відповідь: рівняння не має коренів

VІІІ. Домашнє завдання

Вивчити конспект уроку,

Розв’язати рівняння

Рівень «А»

1)  2) х+=3   3).

Рівень «С»

а) х² +2х=0 ;     б) +х³ =+у³.

 

 

 

Урок 6

Тема уроку: Рівносильні перетворення нерівностей. Метод інтервалів.

Мета уроку: узагальнити поняття рівносильних нерівностей та рівносильних 

                      перетворень нерівностей; сформувати вміння розв’язувати

                      нерівності  методом інтервалів; розвивати вміння  робити

                      висновки; вміння працювати з книгою.

Тип уроку: засвоєння нових знань і вмінь.

 Девіз уроку: «Знати, мислити, вміти, діяти».                               

                          ПЛАН

І.Організаційний етап.

Модуль психологічного супроводу

Прийом «Зразковий стіл»

Перед  початком уроку  оголошується конкурс серед учнів , які сидять за однією партою, на кращу підготовку навчального приладдя та навчальних посібників до уроку. На початку  уроку за результатами конкурсу оголошується «Зразковий стіл»

ІІ. Перевірка домашнього завдання

1.Завдання рівня стандарту учні коментують з місця, завдання академічного рівня  записують на дошці, пояснюючи хід їхнього розв’язування. Учні здійснюють самоперевірку.

2.Інтерактивна вправа «Мікрофон»

- Як записується  в загальному вигляді нерівність з однією змінною х?

(f(x)>g(x))

• Наведіть  приклади нерівностей , які ви вже вмієте розв’язувати.
• Що називається розв’язком нерівності з однією змінною?
• Що означає розв’язати нерівність ?
• Що таке ОДЗ нерівності?
• Які нерівності називаються рівносильними?
• Сформулюйте властивості нерівностей , які дозволяють здійснювати рівносильні переходи на будь-якій множині; на ОДЗ заданої нерівності.
• Які два методи розв’язування нерівностей вам уже відомі7

ІІІ. Пропедевтична практика

Розв’язати рівняння

|х +2| +|у-5| +|2х² -8|=0

Розв’язання

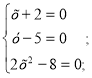
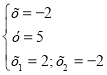  Відповідь (-2;5)

ІV.Орієнтація

 Вчитель повідомляє тему і мету уроку. План вивчення теми

1.Область визначення нерівності.

2.Узагальнення основних властивостей нерівностей.

3.Розв’язування нерівностей за допомогою методу інтервалів.

   Алгоритм розв’язування нерівностей методом інтервалів.

Вчитель  звертає увагу учнів на те, що розв’язувати нерівності  можна двома способами, які подано на схемі

                                 Розв’язування нерівностей

  Метод рівносильних перетворень                   Метод інтервалів

V. Презентація

 Вчитель   пояснює на прикладі розв’язування нерівностей як методом рівносильних перетворень , так і методом інтервалів .

Приклад 1. Розв’яжіть  нерівність .

Метод рівносильних перетворень      Метод інтервалів  

1.ОДЗ: х3.                                      1.ОДЗ: х3.                                     

                               2. f(x) =. Нулі функції:

                                                                       х=-5

 

                                                                                        +           -            +

                                  3.                              -5            3

                                                                                            

 Відповідь : х є  [-5;3)

Метод інтервалів можна застосовувати й для розв’язування  більш складних нерівностей, а також і не строгі нерівності

Приклад 2.Розв’яжіть нерівність (х² -6х +8)   

Розв’язання. Маємо (х-2) (х-4)  

Розглянемо функцію    f(x)= (х-2) (х-4). Область визначення (-;1] [3;+).

 

 

Множина коренів рівняння   f (x)= 0 має вигляд {1;3;4} .

Розв’яжемо    нерівність f(x)>0.Нулі функції  розбивають її область визначення на такі проміжки  знакосталості : (- ;1), (3;4),(4;+).

Установлюємо, що множина : (- ;1) (4;+) є множиною розв’язків  нерівності f(x)>0.Об’єднавши  множини розв’язків рівняння f (x)= 0 і нерівності f(x)>0, отримаємо відповідь.

Відповідь: (- ;1) (4;+){3}.

Алгоритм розв’язування  нерівностей методом інтервалів:

1.Знайти ОДЗ.

2.Знайти нулі функції: f(x)=0.

3.Позначити нулі на ОДЗ і знайти знак функції f(x) у кожному проміжку, на які розбивається ОДЗ.

4. Записати відповідь , враховуючи знак заданої нерівності.

Отже ,множиною розв’язків нестрогих нерівностей є об’єднання множини розв’язків нерівності і множини коренів рівняння.

Означення. Розв’язком  нерівності із змінною називається значення змінної , яке перетворює задану нерівність на правильну числову нерівність.

Розв’язати  нерівність –означає знайти всі її розв’язки або довести , що їх немає.

Областю допустимих значень  нерівності називається спільна область визначення для функцій, що стоять у лівій і правій частинах нерівності.

   VІ.Практика на прикладах

1. №250

1)-колективне розв’язання

2-3) – робота в парах

VІІ  . Керована практика.

Рівень «С»                Рівень «А»

№250 (4-6)                 №257

VІІІ. Незалежна практика

Рівень «С»                    Рівень «А»

№252 (1-2)                     №260 (1-5)

ІХ. Підсумок уроку

1.Сформулюйте план розв’язування нерівності методом інтервалів.

2. Визначте ОДЗ , нулі нерівності 

3.Розвяжіть нерівність:

(х-2)(х+3)

Х.Домашнє завдання

Вивчити §12.

Рівень «С» № 253

Рівень «А» №261(1-4). № 263 (1-2)

 

 

 

 

Урок 7

Тема .Рівняння і нерівності, що містять знак модуля.

Мета : розглянути способи розв’язування рівнянь і нерівностей , що             

            містять знак модуля;

             розвивати логічне мислення, вміння порівнювати, аналізувати;

             виховувати загальнолюдські духовні цінності.

 Тип уроку: засвоєння нових знань і вмінь

                                                             Хто з дитячих років вивчає

                                                              математику, той розвиває увагу,

                                                              тренерує свій розум, свою волю,

                                                             виховує в собі  наполегливість  в   

                                                               досягненні мети

                                                                                              Маркушевич А.І.

 

 

                                   ПЛАН

І.Організаційний етап.

Модуль психологічного супроводу

Прийом «Посмішка».

ІІ. Пропедевтична практика

1.Виконання тестових завдань

1. Розв’яжіть нерівність

А) (-(-5; +; б) [-11;-5]; в) [-11;-5); г) (5;11].

2.Знайдіть найбільший цілий від’ємний розв’язок нерівності х² +2х-3>0.

а) -3;б)-1; в)-5;г)-4.

3.Знайдіть найбільший цілий  розв’язок нерівності х² (х-1)(х+2)

А) 14 б)-1; в) 2; г)0.

4.Знайдіть найменший цілий розв’язок нерівності .

А) 3 ; б) 4; в) 1; г)2.

2.Робота в групах:

І група:

1.Позначте на числовій прямій числа, модуль яких  дорівнює 3.

2. Позначте на  числовій прямій точки. Відстань від яких до точки 1 дорівнює 3.

3.Розвяжіть рівняння

 |3- х|=9

ІІ група

 1.Дайте означення модуля числа а.

2. Запишіть за допомогою модуля речення:  «Відстань від точки х до 5 дорівнює 2».Знайдіть усі такі точки х.

3. Запишіть вираз  без знака модуля: а) |3-|; б)  |2³ -3²|; в)  |х-3|; г) |х+4|; д) |5-х|;

ІІІ. Орієнтація

 Повідомлення  теми і мети уроку.

           План  вивчення теми

1. Розв’язування рівнянь та нерівностей  з модулями:

1)за означенням  модуля;

2) за геометричним змістом;

3) за загальною схемою:

ІV. Презентація

Основний матеріал учні записують  у формі опорного конспекту Вчитель  на прикладах показує як розв’язуються рівняння і нерівності з модулями.

Розв’язування рівнянь та нерівностей з модулями

1.За означенням

 

 |а| =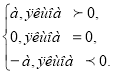

2.За геометричним змістом

|а|- відстань на числовій прямій від точки 0 до точки а.

1.| f(x)|=а.                         3. | f(x)| > а.                        

2.| f(x)|= | g(x)|                4. | f(x)| < а.                        

3. За загальною схемою

1. Знайти ОДЗ.

2.Знайти нулі  всіх під модульних функцій.

3.Позначити нулі на ОДЗ і  розбити ОДЗ на проміжки.

4 Знайти  розв’язок у кожному з проміжків ( і перевірити , чи входить  цей розв’язок у розглянутий проміжок) .

Приклад1. Розв’яжіть рівняння |х-1|=2 .

Розв’язання .

Використовуючи властивість, якщо  |а| = в , то а = в або а = -в    перейдемо до сукупності рівнянь

  звідси   Відповідь: -1; 3.

Приклад 2.  Розв’яжіть рівняння |2х-1|= 3х +1 .

Розв’язання .

Якщо замінити дане рівняння на сукупність рівнянь

то отримаємо два значення змінної х: -2 і 0. Але  -2 не є коренем даного рівняння . Це сторонній корінь.

Тому дане рівняння  рівносильне системі

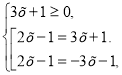  яка має єдиний розв’язок  х= 0.

Отже рівняння виду  | f(x)|=g(х) рівносильне  системі

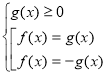                     або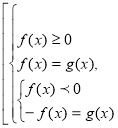

Нерівність  виду  |х| < а рівносильна системі

 Нерівність виду  |х| > а  рівносильна сукупності нерівностей

 

                                                                                      

 Нерівність  виду | f(x)| g(х) рівносильна системі

Нерівність  виду | f(x)| > g(х) рівносильна сукупності нерівностей

Приклад 3.Розв’яжіть нерівність |4х-3|>5 .

Розв’язання.

Дана  нерівність рівносильна сукупності нерівностей

   Звідси  

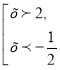
Відповідь: (-

V. Практика на прикладах .

Усно №292.

№301(1-2)

VІ. Керована практика.

 «С» №302(1-2)               «А» № 304

VІІ. Незалежна  практика

«С»  №298           «А» №307

VІІІ.   Підсумок уроку

 Алгоритм розв’язування рівнянь:

-  за означенням

- за геометричним змістом

-за загальною схемою

ІХ. Домашнє завдання

 Вивчити §14

Рівень «С» №299,302(3-4)

Рівень «А» №305, 308

 

 Урок 8.

Тема .Контрольна робота  з теми «Функції, їхні властивості і

                                                            графіки»

Мета уроку: перевірити рівень знань, умінь і навичок учнів з цієї теми.

Тип уроку: контроль і корекція знань, умінь і навичок.

                                                План

І Організаційний етап.

Учитель налаштовує учнів на роботу, видає їм текст з умовами завдань контрольної роботи.

ІІ. Виконання контрольної роботи

Варіант 1

Рівень «А»

1.Розв’язати нерівність

;

2.Знайдіть область визначення функції

у=.

3.Знайдіть проміжки зростання і спадання функції у=-х² -4х-3 та її найбільше значення

4.Побудуйте графік функції

 у=(х+1)² -3

 

 

Рівень «С»

1.Побудуйте графік функції

 у=|х-5|.

2.Знайдіть область допустимих значень  рівняння

=0

3.Дослідіть на парність функцію

у= х⁵ +2х ; у= 6х⁶ -7х⁵.

4.Знайдіть функцію обернену до даної. Побудуйте графіки цих  функцій.

       у=  -3х +4.

5.Знайдіть область значень функції у=х² -4.

 

Варіант 2

Початковий та середній рівні навчальних досягнень

У завданнях 1-6 виберіть правильну відповідь

1.f(x)=-x² +4. Яка з наведених рівностей неправильна?

А) f(1)=3; б) f(-1)=3; в) f(-2)=0; г) f(2)=8

2.Яке з наведених чисел не входить до області визначення функції

f(x)=?

а) 1; б) 0; в) -3; г) -7.

3.Множиною значень якої з наведених функцій є проміжок (-;5]?

А) f(x)=х+5; б) f(x)=;в) f(x)=х² -5; г) f(x)=-х² +5.

4.Графік якої з наведених функцій симетричний відносно осі Оу?

А) у=х+1; б) у=х² +1; в) у=;  г) у=х² –х.

5.Яке з наведених рівнянь рівносильне рівнянню -1=0?

А) ; б) 3-х=0; в) х-3=0 ; г)

Достатній рівень навчальних досягнень

7.Укажіть , які геометричні перетворення графіка функції f(x)= необхідно виконати , щоб одержати графік функції f(x)=.Побудуйте цей графік.

8.Застосовуючи властивості функцій, розв’яжіть рівняння .

Високий рівень навчальних досягнень.

9. Розв’яжіть рівняння |2х-3|=х

ІІІ. Підсумок уроку.

ІV.Домашнє завдання.

Виконати задачі (обмінятись варіантами)

 

 

Тема розділу стереометрії: Паралельність у просторі.

Клас:   10

 Тема уроку: Взаємне розміщення двох прямих у просторі

Мета: розглянути всі випадки взаємного розміщення прямих у просторі; сформувати поняття про мимобіжні прямі; вивчити ознаку мимобіжних прямих та сформу­вати вміння застосовувати цю ознаку під час роз­в'язування задач; формувати в учнів уміння критично оцінювати подану інформацію, прагнення до ділового співробітництва.

Тип уроку: засвоєння нових знань.

Обладнання: стереометричний набір тіл, кодоскоп, таблиця.

                                                  План

І. Пропедевтична практика

Оскільки на попередньому уроці учні виконували само­стійну роботу, а домашнім завданням було розв'язуван­ня задач іншого варіанта, то перевірка домашнього зав­дання одночасно є й аналізом самостійної роботи.

Правильність виконання тестових завдань (І рівень) учні перевіряють за готовою таблицею з правильними відповідями.

 

№ завдання	Варіант 1	Варіант 2
.1	г	б
2	г	в
3	в	в

Завдання II і III рівнів перевіряємо за готовими рисун­ками. Оскільки всі пропоновані завдання — задачі на доведення, то для економії часу можна не заслуховувати розв'язання всіх десяти задач. Достатньо шляхом фрон­тальної роботи, ставлячи учням запитання, перевірити рівень усвідомлення більш важливих моментів вивче­ного матеріалу.

Як приклад наведемо запитання до задачі 1 (Варіант 1, III рівень)

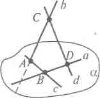
1. Яким способом можна до­вести, що прямі с і d не пе­ретинаються? (Способом від супротивного)                                                                                                                         
2. Якщо припустимо, що прямі с іd  перетинаються, то що можна сказати про їх розміщення? (Обов'язково належать одній площині, наприклад площині .)
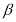3. Де будуть знаходиться точки А і В? (Оскільки с 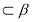, А є с, В є с, то А 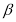є і В є .)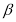

4.  Де будуть знаходитися точки С і D? (С є , D є )

IІ Запитання до класу

1. Чи можуть дві різні прямі мати дві спільні точки? А три? Відповідь обгрунтуйте.
2. Чи можуть дві різні прямі мати одну спільну точку? Як називаються такі прямі?
3. Чи можна провести площину через дві прямі, що пе­ретинаються? Скільки таких площин можна про­вести? Відповідь обгрунтуйте.
4. На рисунку зображено куб АВСВ А₁ В₁ С₁  D₁. Чи ма­ють спільну точку прямі АА₁   і ВВ_1; АА₁ і ВС?Як називаються прямі АА_{1 і} ВВ₁; АА₁ і ВС?

Виникає проблемна ситуація: прямі АА₁   і ВС, як і прямі

не перетинаються, але не є паралельними.

Отже, треба дати означення таким-прямим, як АА₁    і ВС, і переглянути означення паралельності прямих у просторі.

ІІІ. Орієнтація.

Повідомлення теми, мети уроку. Мотивація навчальної діяльності

 

IV. Презентація

1. Паралельні прямі

Учні порівнюють означення паралельних прямих на площині та в просторі, при цьому встановлюють, що в «просторовому означенні» необхідною умовою пара­лельності двох прямих є те, що вони лежать в одній пло­щині. Отже, існує спільне між паралельними прямими та прямими, що перетинаються, — такі прямі задають пло­щину й до того ж тільки одну. Таким чином, до вже відо­мих способів задання площини можна додати ще один: площину можна задати двома паралельними прямими.

2. Мимобіжні прямі

Означення. Дві прямі, які не лежать в одній площині, на­зиваються мимобіжними.

(Якщо учні вивчають геометрію за підручником Погорєлова О. В., то доцільно поставити перед ними про­блемне завдання: проаналізуйте означення мимобіж­них прямих (за підручником), знайдіть «зайве» в ньому, відповідь обґрунтуйте і дайте правильне, на ваш погляд, означення. Таку роботу можна організувати в парах.)

3. Взаємне розміщення двох прямих у просторі

На цьому етапі вивчення нового матеріалу обов'язко­вим є побудова схеми взаємного розміщення прямих. Залежно від підходу до класифікації взаємного роз­міщення прямих у просторі схеми можуть бути такими.

Схема 1

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

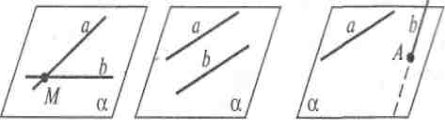
                                                   Дві прямі мають одну

                                                спільну точку –перетинаються.                                                                                                                    

                                                                                                                  Дві прямі не мають

                                                                                                                         спільних точок.

Дві прямі мають дві спільні

точки-співпадають.

 

 

 

 

 

 

 

 

 

 

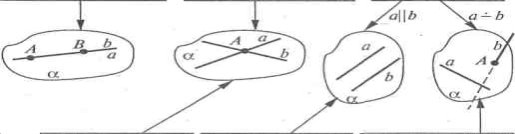
Прямі а і в задають єдину      площину.                          Прямі а і в не лежать в одній 

                                                                                                     площині

 

Схема 2.

 

4. Ознака мимобіжних прямих

Формулювання теореми про мимобіжні прямі немає в підручниках [2;3]. тому необхідно дати учням цю оз­наку та організувати роботу з її доведення таким чином: заздалегідь обирається творча група (з учнів з високим рівнем навчальних досягнень), яка отримує завдання: доведіть, що якщо пряма а лежить у площині , а пряма в перетинає площину в точці М, яка не належить а, то прямі а і в — мимобіжні.

Творча група отримує також картку-орієнтир з планом доведення і рисунком, за яким і доводить ознаку ми­мобіжних прямих. Звіт творчої групи проходить у ви­гляді презентації доведення ознаки за заздалегідь підго­товленими записами та рисунком. Учні класу запису­ють формулювання і доведення ознаки мимобіжних прямих у зошити.

V. Практика на прикладах

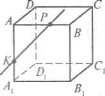
Задачі за готовими записа­ми розв'язуються фрон­тально.

Задача 1. Користуючись    рисунком 1, знайдіть по­милки в таблиці     

 

 

 

         

Прямі	АВ	ВВ,	А А
КР С1А1 С1В	Перетинаються Мимобіжні Перетинаються	Мимобіжні Мимобіжні Перетинаються	Перетинаються Перетинаються Мимобіжні

Визначте :

а) розміщення прямих  В₁С₁ і ВС; DD₁ і СС₁

б) розміщення прямих СС₁ і АВ; АD і ВВ₁.

 

Задача 2. Чи перетинаються прямі:

а) АС₁ і ВВ₁ {рис. 2); б) АD і ВМ (рис. 3)? Відповідь обгрунтуйте.

 

 

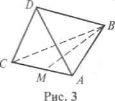
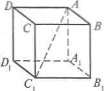
Рис 2.                                             

VI. Керована практика

Задача 1.Доведіть, що всі прямі, які перетинають кожну із двох паралельних прямих, лежать в одній площині.

План-підказка

1.Оскільки прямі  а і в  паралельні, то вони визначають….

2.Нехай с-довільна пряма, яка перетинає пряму а у точці А, а пряму в- у точці В. Точки А і В лежать у площині…

3.Оскільки дві точки прямої с лежать у площині…, то й пряма с…

4. Таким чином, усі прямі, які …дві дані паралельні прямі….

Задача 2.Прямі МN і КL перетинаються. Чи можуть  перетинатися прямі МК і NL? Чи можуть вони бути паралельними?

 

VIІ. Незалежна практика

Рівень «С» № 206,208,209

Рівень «А»№ 214, 216,218

 

  VIІІ. Підсумки уроку

Підсумки уроку підбиваються під час фронтальної бесіди.

Завдання 1. Укажіть зайві слова (якщо вони є) в таких твердженнях:

1. дві прямі називаються прямими, що перетинаються, якщо вони мають єдину спільну точку і лежать в одній площині;
2. паралельними прямими називаються прямі, які ле­жать в одній площині і не перетинаються;
3. мимобіжними називаються прямі, які лежать у різ­них площинах і не перетинаються.

 

  Завдання 2. Сформулюйте ознаку мимобіжних прямих та твердження, обернене до неї.

VII. Домашнє завдання

Вивчити §6.

Рівень «С» №211,212

Рівень «А» №221,224

 

 

УРОК №2

Тема: Ознаки паралельності прямих

Мета: засвоїти ознаку паралельності прямих ;

            сформувати навички її застосування до розв’язування задач;

           працювати над формуванням критичного мислення.

 Тип уроку: засвоєння нових знань.

 Обладнання: ПК

                                        План

 І. Пропедевтична практика

1.Графічний диктант

Чи правильні  такі твердження?

1.Якщо дві прямі в просторі не перетинаються, то вони паралельні.

2Якщо дві прямі на площині не перетинаються, то вони паралельні.

3. Якщо прямі а і в не лежать в одній площині, то вони можуть бути паралельними.

4. Якщо прямі а і в не лежать в одній площині, то вони можуть бути мимобіжними.

5.Якщо а і в –прямі, які лежать в одній площині, то існує пряма с, що перетинає як пряму а, так і пряму в.

6. Якщо прямі а і в не лежать в одній площині, то через пряму а обов’язково можна провести площину, що перетне пряму в.

Відповіді.

2. 4,5,6, так. 1.3-ні

1.Самостійна  робота.

Задача 1. Доведіть, що якщо прямі АВ і СД мимобіжні, то й прямі АС і ВД також мимобіжні.

Задача 2. Чи можна через точку С, що не належить мимобіжним прямим а і в, провести дві різні прямі, кожна з яких перетинає прямі а і в? Відповідь обґрунтуйте.

Перевірку задачі 1,2 здійснюємо за допомогою кодоскопа.

2. Теоретична розминка

1. Сформулюйте відомі твердження про паралельність прямих на площині.
2. Сформулюйте теорему про дві прямі, паралельні до третьої. Знайдіть на предметах, що вас оточують, її просторовий аналог.

3. Орієнтація

 Повідомлення  теми, мети уроку

Задача. Площина не перетинає паралелограм АВСВ. Через вершини паралелограма проведено паралельні прямі, які перетинають площину  у точках А₁,В₁,С₁, В_х (див. рис.)ЗнайдітьДД₁,

, ВВ₁  =в,СС₁=с.

Коментування умови задачі можна провести у формі міні-диспуту, в якому беруть участь «експерти». Експертна група організовується заздалегідь.

Учитель. Я не зовсім розумію умову задачі. Що озна­чає

«АА₁, ВВ₁, СС_І і ДД_] — паралельні прямі»? До цього моменту ми розглядали дві паралельні прямі, тут же їх — чотири!

1-й експерт. Можливо, всі ці прямі паралельні одна одній?  '

2-й експерт. Як це розуміти?

3-й е к с п е р т. Я розумію це так: якщо АА₁ \\ВВ_І, ВВ₁ \\СС₁, то А1_Х \\СС₁ і т. д. Адже це ми доводили в сьо­мому класі.

4-й експерт. Я не згоден. Ця теорема доведена для прямих, які розташовані в одній площині, а прямі АА₁, ВВ₁, СС₁ і ДД₁ знаходяться в різних площинах.

Учитель. Саме це і є проблемою. Давайте сформу­люємо й доведемо аналог планіметричної ознаки пара­лельності прямих для простору.

IV. Презентація

Доведення теореми проводиться у формі евристичної бесі­ди. Вчитель оцінює роботу учнів під час вивчення ознаки.

V. Практика на прикладах

Письмове розв'язування задач

№251. 252.

Усно.№244,245,246

    VІ.       Керована практика

 Рівень «А» №254,255

Рівень «С» № 249,250

VIІ. Підсумки уроку

Кожний учень отримує картку із завданням. Самостійна робота

Укажіть паралельні прямі на рисунках

 

Математичний диктант

Із наведених тверджень виберіть правильні:

1. якщо прямі а і е, перетинаються, то вони обов'яз­ково паралельні;
2. якщо пряма перетинає одну із двох паралельних прямих, то вона перетинає й іншу;
3. якщо прямі а і в не паралельні одній і тій самій прямій, то вони не паралельні між собою;
4. паралельні прямі можуть лежати відповідно у двох площинах, що перетинаються;
5. якщо пряма с перетинає дві паралельні прямі а і в,то прямі а,в і с обов'язково лежать в одній площині;

Примітка. У зошитах учні записують тільки номери правильних тверджень. Усі необхідні для розв'язання задач рисунки учні виконують на чернетках.

Відповідь. 4; 5.

Для неправильних тверджень учитель заздалегідь при­готував рисунки-контрприклади, за якими потім і здійснюється перевірка математичного диктанта.

 

 

        VII. Домашнє завдання

Вивчити §7

Рівень «А» №259,258

Рівень «С» №247,248

 

 

 

Література:

1.Журнал «Математика в школах України» 2010р.№14,28,8,31

Проектування уроку математики в умовах компетентнісно орієнтовааного навчання. Проєктування уроку .

2.Т.Л.Корнієнко,В.І.Фіготіна. Геометрія  10 клас. Академічний рівень. «Ранок» м.Харків 2010.

3. Г.П.Бевз, В.Г.Бевз.Геометрія.10 клас. К.: Генеза, 2010

4. А.Г.Мерзляк .Алгебра і початки аналізу. Профільний рівень. .: Гімназія,2010

5. Т.Л.Корнієнко,В.І.Фіготіна. Алгебра і початки аналізу. Академічний рівень. «Ранок» м.Харків 2010.