ВИМІРЮВАННЯ ТА ПОБУДОВИ НА МІСЦЕВОСТІ

МІНІСТЕРСТВО ОСВІТИ І НАУКИ УКРАЇНИ

ВІДОКРЕМЛЕНИЙ СТРУКТУРНИЙ ПІДРОЗДІЛ МОГИЛІВ-ПОДІЛЬСЬКИЙ ТЕХНОЛОГО-ЕКОНОМІЧНИЙ ФАХОВИЙ КОЛЕДЖ

ВІННИЦЬКОГО НАЦІОНАЛЬНОГО АГРАРНОГО УНІВЕРСИТЕТУ

 

 

 

 

 

 

 

 

 

 

 

 

 

МЕТОДИЧНА РОЗРОБКА ЗАСІДАННЯ

 ІНФОРМАЦІЙНО-ТЕХНІЧНОГО ГУРТКА

 

 

 

 

 

 

 

 

 

 

2020

ТЕМА. ВИМІРЮВАННЯ ТА ПОБУДОВИ НА МІСЦЕВОСТІ

МЕТА. Прищеплення інтересу до вивчення геометрії. Навчити студентів застосовувати властивості геометричних об’єктів  та вимірювальні вміння на практиці

Вступне слово викладача. Для практичних цілей часто виникає необхідність проводити геометричні побудови на місцевості. Такі побудови потрібні і при будівництві будівель, і при прокладанні доріг, і при різних вимірах об'єктів на місцевості. Можна подумати, що робота на рівній поверхні землі (а саме такою  ми і будемо її вважати у всіх завданнях цього параграфа) нічим, по суті, не відрізняється від роботи циркулем і лінійкою на звичайному аркуші паперу. Це не зовсім так. Адже на папері циркулем ми можемо проводити будь кола  або їх дуги, а лінійкою - будь-які прямі. На місцевості ж, де відстані між точками досить великі, для подібних дій знадобилася б довга мотузка або величезна лінійка, які не завжди є під руками. Та й взагалі креслити прямо на землі, які б то не було лінії - дуги або прямі - представляється досить складним. Таким чином, побудови на місцевості мають свою специфіку.

Проведення прямої, паралельної даній прямій. На місцевості є такі три дані точки А, В і С, що не лежать на одній прямій. Через точку А прокладемо пряму, паралельну прямій ВС.

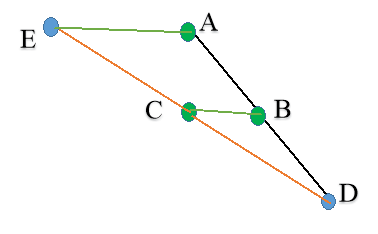Продовжимо пряму АВ за точку В і відкладемо на ній точку D на відстані АВ від точки В (рис. 1). Продовжимо пряму CD за точку С і відкладемо на ній точку Е на відстані CD від точки С. Тоді відрізок АЕ буде паралельний відрізку ВС, що є середньою лінією трикутника ADE. Запропонований спосіб вигідно відрізняється від безлічі інших способів, що спираються па вимірювання кутів чи розподіл відрізка навпіл.

 

 

 

                                      

 

 

                                                 Рисунок 1

 

 

Поділ відрізка навпіл.

       Знайти середину відрізка АВ, заданого на місцевості двома точками А і В. Візьмемо якусь точку С, що не лежить на прямій АВ. Продовжимо пряму ВС за точку С і відкладемо на ній точку D на відстані 2ВС від точки С (рис. 2). Продовжимо пряму AD за точку А і відкладемо на ній точку Е на відстані AD від точки А. Бажана середина F відрізка АВ лежить на його перетині з прямою ЄС. Дійсно, відрізок СЕ паралельний відрізку AG - середньої лінії трикутника CDE (тут G - середина відрізка CD). Так як, крім того, BC = CG, то CF - середня лінія трикутника ABG, звідки AF = FB.

Може здатись, що наведений спосіб знаходження середини відрізка  не є найпростішим. Однак його переваги добре проявляться, коли буде задача ділити відрізок не тільки на дві, але і на будь-яке число рівних частин.

 

 

 

 

 

 

 

 

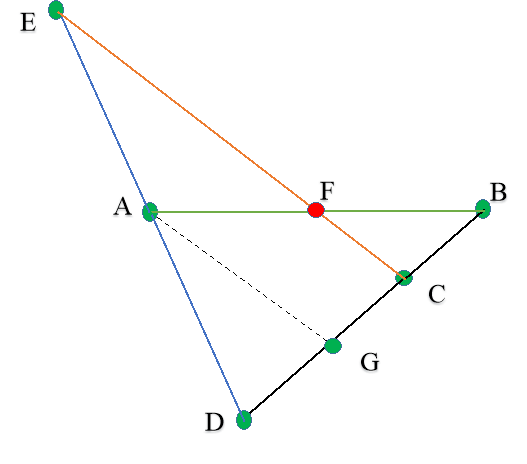
Рисунок 2

 

 

 

 

 

 

 

 Побудова бісектриси кута

На місцевості є такі три точки А, М і N, що не лежать на одній прямій. Прокласти бісектрису кута MAN?

Виберемо на одній стороні даного кута (рис. 3) точки В і С, а на іншій точки D і Е так, щоб виконувалися рівності    AB = ВС = АD = DE

Знайдемо точку  перетину прямих BE і CD. Тоді пряма АТ буде шуканої бісектрисою, оскільки в трикутник АСЕ бісектриса AT є одночасно і медіаною, а значить, проходить через точку  перетину медіан ЕВ та CD.

 

 

 

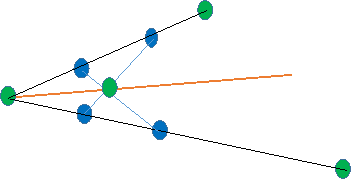
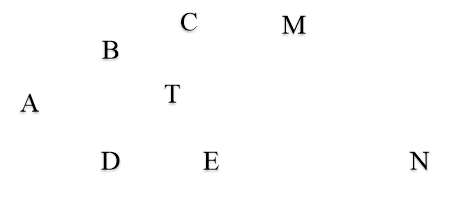
Рисунок 3

 

 

 

 

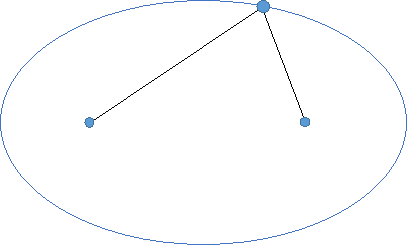
Зображення еліпса на місцевості.

Використовуючи основну властивість еліпса (сума відстаней від деякої його точки до двох фокусів є величина постійна і дорівнює 2а – великій осі еліпса) можна накреслити еліпс на будь-якій місцевості, поверхні. Для цього закріпимо два кілочки, до яких за кінці прив’яжемо мотузку такої довжини, якою хочемо бачити більшу вісь еліпса. Натягуємо закріплену мотузку за допомогою або третього кілка або за допомогою крейди і тримаючи весь час в натягнутому стані, викреслюємо овал по один бік відносно обох кілків, а потім по інший від них бік. Так можна накреслити клумбу або газон у формі еліпса.

 

 

 

 

                                                                            

 

 

Рисунок 4

 

 

Визначити довжину свого кроку, щоб згодом вимірювати відстані кроками досить легко. Найпростіший і, здавалося б, точний спосіб полягає в тому, щоб зробити один крок і виміряти відстань між крайніми (найбільш віддаленими) точками двох ступень. Такий спосіб явно не годиться з двох причин. По-перше, відстань між крайніми точками ступень не дорівнює довжині кроку, а перевершує її на довжину однієї ступні (правильніше було б виміряти відстань, наприклад, між носками двох ступень). По-друге, при всьому старанні навряд чи можна зробити один звичайний крок - для цього вам потрібно опинитися в стані звичайної ходьби.

Для визначення довжини кроку достатньо пройти якесь заздалегідь відоме і не надто коротку відстань, скажімо між сусідніми кілометровими або стометровими стовпчиками на шосе, і поділити цю відстань на кількість зроблених кроків.

Відзначимо, що середня довжина кроку дорослої людини приблизно дорівнює половині його зросту, рахуючи до рівня очей.

Вимірюючи будь-які довжини пальцями руки, краще не відривати руку від вимірюваної поверхні, а приставляти один палець до іншого, який потім знову витягати в заданому напрямку (описаний процес віддалено нагадує рух гусениці). Щоб знайти довжину такого розмаху своїх пальців, найпростіше відкласти уздовж якої-небудь прямої одні або кілька десятків розмахів пальців, а потім поділити на їх кількість відкладену в результаті довжину.

Цікавий факт.

 Всесвітньо відомий письменник Артур Конан Дойль був лікарем. Але він дуже добре, мабуть, знав геометрію. В оповіданні "Обряд родини Масгрейвів" він описав, як Шерлоку Холмсу потрібно було визначити, де будуть кінець тіні від в'яза, який зрубали. Він знав висоту цього дерева раніше. Шерлок Холмс так пояснив свої дії: "... я пов'язав разом два вудилища, що дало мені шість футів, і ми з моїм клієнтом відправилися до того місця, де колись ріс в'яз. Я встромив дану конструкцію  в землю, зазначив напрямок тіні і виміряв її. У ній було дев'ять футів. Подальші мої обчислення були вже зовсім нескладні. Якщо палиця заввишки в шість футів відкидає тінь у дев'ять футів, то дерево заввишки шістдесят чотири фути відкине тінь в дев'яносто шість футів, і напрямок тієї й іншої, зрозуміло, збігатиметься ".

Важливо знати, що в сонячний день можна користуватися будь-якою тінню, якою б довжини вона не була. Вимірявши свою тінь або тінь якогось жердини, обчислюють шукану висоту з пропорційності зросту до тіні об’єкту:  AB: ab = BC: bc

Тобто висота дерева у стільки разів більша вашої власної висоти (або висоти жердини), у скільки разів тінь дерева довше тіні людини (або тіні жердини). Це випливає з геометричного подібності трикутників ABC і abc (по двох кутах).

Визначення відстаней за лінійними розмірами   предметів полягає в наступному. Лінійкою, розташованою на відстані 50 см від очей, вимірюють у міліметрах висоту предмета, що спостерігається. Потім висоту предмета в сантиметрах ділять на виміряну лінійкою в міліметрах, результат множать на постійне число 5; отримують відстань до предмета в метрах.

Наприклад, телеграфний стовп висотою 6 м затуляє на лінійці відрізок 10 мм. Отже відстань до нього:

Визначення висоти дерева. Для цього використовуємо косинець у формі прямокутного рівнобедреного трикутника, або створюємо такий трикутник підручними способами з паперу. Катет один косинця тримаємо вздовж стовбура дерева і починаємо відходити від дерева до тих під поки цей катет не стане рівним із деревом. Тоді зафіксувати зором точку на місцевості, де закінчується інший катет. Відстань від даної точки до дерева і буде висотою цього дерева, якщо до неї додати зріст людини, яка здійснювала вимірювання,  до очей.

Визначення відстані за співвідношенням швидкості звуку і світла. Звук розповсюджується у просторі зі швидкістю 330 м/сек.., або 1 км за 3 сек., а світло - практично миттєво. Таким чином, відстань у кілометрах до місця, де пролунав постріл, дорівнює числу секунд, які пройшли від моменту спалаху до моменту, коли був почутий звук пострілу, поділеному на 3.

Наприклад, спостерігач почув звук пострілу через 11 сек. після спалаху. Відстань до місця спалаху: d = 11:3 = 3,7 км.