Властивості степеня (продовження). Частка степенів з однаковою основою

Тема. Властивості степеня (продовження). Частка степенів з однаковою основою

Мета: домогтися свідомого розуміння учнями властивостей степеня з натуральним показником (частка степенів) та виробити вміння застосо­вувати ці властивості для спрощення виразів разом з іншими властивостя­ми степеня, вивченими раніше.

Тип уроку: засвоєння знань, умінь та навичок.

Хід уроку

I. Перевірка домашнього завдання. Актуалізація опорних знань

Бліцконтроль

1. Яка з рівностей є правильною:

1) 2⁴ · 2³ = 2¹²; 2) 2⁴ · 2³ = 4¹²; 3) 2⁴ · 2³ = 4⁷; 4) 2⁴ · 2³ = 2⁷?

2. Запишіть у вигляді степеня з основою х:

1) х⁵ · x³; 2) х⁴ · x; 3) х⁴ · х⁵ · х; 4) хⁿ · х · х^m.

3. Запишіть у вигляді степеня з основою 2:  2²ⁿ · 4:

1) 8²ⁿ; 2) 2²ⁿ⁺¹; 3) 6²ⁿ; 4) 2²ⁿ⁺².

Після проведеного блщконтролю перевіряємо якість його виконання і пропонуємо учням пояснити виконані дії (повторюємо основну власти­вість степеня; означення степеня з натуральним показником).

II. Робота з випереджальним домашнім завданням

Завдання:

1. Відомо, що ab = с. Які правильні рівності випливають з даної рівності? При яких а і b це буде правильним?
2. Відомо, що а³ · a² = а⁵. Які правильні рівності випливають з неї? За яких умов ці рівності будуть правильними?

 Зрозуміло, що більшість учнів із завданням 1) впорається легко, бо якщо  ab = с, то , (а і b не дорівнюють 0).

Якщо ця частина завдання виконана, то завдання 2) за аналогією при­водить до висновків:

Якщо а³ · а² = а⁵, то а⁵ : а² = а³ (*); а⁵ : а³ = а² (**), якщо ні а³, ні а² не дорівнюють нулю.

III. Засвоєння знань

 Домогтися свідомого розуміння учнями наступної властивості мож­на, виконавши роботу з порівняння за алгоритмом (див. додаток) здобутих виразів: а³ · a² = a⁵; a⁵ : a² = а³; а⁵ : а³ = а².

Після    проведеного    порівняння    і    корекції    виконаної   учнями самостійної роботи доходимо висновків:

1. Під час ділення степенів з однією основою основа не змінюється, а від показника діленого віднімаємо показник дільника. (Якщо показ­ник діленого більший за показник дільника.)
2. Основа степеня при діленні повинна бути відмінною від 0.

Особливі випадки застосування цієї властивості виводимо з практич­них завдань.

Завдання. Спростіть вираз. 1) а⁵: а⁵; 2) а⁵ : а⁷.

Знову звертаємось до порівняння, а з цього виникає необхідність уточнення сформульованої властивості, а саме:

1) якщо а^m · аⁿ = а⁰ = 1, тобто а⁰ = 1 (а ≠ 0);

2) якщо m < n, то і ділимо .

Усі висновки учнів записують у зошити в стислому вигляді.

IV. Застосування знань

 На цьому уроці концентруємо увагу на розумінні учнями власти­вості степеня, що випливає з основної властивості степеня. Тому не вимагаємо від учнів відтворення алгоритмів, але пояснювати дії учні повинні.

Виконання усних вправ

1. Поясніть, чому дії виконані саме так:

1) а⁸ : а⁴ = а^{8 – 4} = а⁴; 2) ; 3) а⁸ : а⁸ = а^{8 – 8} = а⁰ = 1.

Яким є значення а (за змістом завдання)?

2. Яка з рівностей є неправильною:

1) 2⁷ : 2⁵ = 2² = 4; 2) 3⁷ : 3⁶ = 1; 3) ; 4) 5² : 25 = 1?

3. Подайте у вигляді степеня частку:

1) a⁸ : a²; 2) 3⁴ : 3; 3) x⁶ : x; 4) ; 5) -z⁶ : (-z)³.

4. Який вираз необхідно поставити замість *, щоб здобути правильну рівність: a¹⁵ : * = a⁵?

Виконання письмових вправ

1. Подайте у вигляді степеня частку:

1) a²¹ : a¹⁷; 2) b⁹ : b; 3) b¹¹ : b¹¹; 4) (a – b)¹⁵ : (a – b)¹¹.

2. Замініть * степенем з основою а, щоб рівність була правильною:

1) а¹⁴ : * = а⁶; 2) * : а¹¹ = а²¹; 3) * : а⁷ · а¹¹ = а¹⁸; 4) а⁹ : * : а = а³.

3. Обчисліть значення  виразів  (у разі  необхідності  звертаємось до довідкових таблиць).

1) 2^{2 ·} 2³; 2) 3¹⁵ : 3¹¹; 3) 5⁹ · 5³ : 5¹⁶; 4) 11¹¹ : 11¹⁰ · 11;

5) 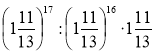; 6) ;  7) 3² : 81; 8) 256 : 2⁵ · 2².

4. Подайте у вигляді степеня вираз (n — натуральне число):

1) х²⁷ : х, п ≤ 17;  2) хⁿ : (х¹⁰ : х¹²), п ≥ 7;

3) x⁵ⁿ : x³ⁿ · х⁴ⁿ⁺²;  4) (х³ ·х³ⁿ)(х²ⁿ · х²ⁿ).

V. Підсумок уроку. Рефлексія

Закінчіть речення, щоб вони стали істинними:

1. Щоб поділити 2⁵ на 2³, треба...
2. Щоб поділити 3⁷ на 3¹⁰, треба...
3. Щоб поділити 7¹⁵ на 7¹⁵, треба...

VI. Домашнє завдання

№ 1. Подайте у вигляді степеня:

1) a^l2 : a⁴; 2) c⁸ : c; 3) b⁵ : b⁵; 4) (a+b)ⁿ : (a+b)⁷; 5) 3¹³ :3⁶; 6) 7⁵ · 7¹² : 7¹⁴;

7) 37⁸ : 37⁷ · 37; 8) 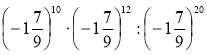; 9) х³ⁿ : х^2п · х^5n–1.

№ 2. Обчисліть значення виразу:

1) ; 2) ; 3) ; 4)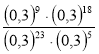

№ 3. Випереджальне домашнє завдання. Що називають степенем чис­ла з натуральним показником? Що називають основою степеня? показни­ком степеня? (Знайдіть у підручнику.)

Використовуючи знання, набуті раніше, назвіть основу й показник степе­ня, прочитайте вираз за допомогою слів та запишіть вираз у вигляді добутку:

а⁵

(а²)⁵

(аⁿ)⁵

(аⁿ)^m

Яку властивість множення можна використати, щоб спростити утво­рений добуток? Виконайте множення та порівняйте відповіді. Якого ви­сновку ви дійшли?