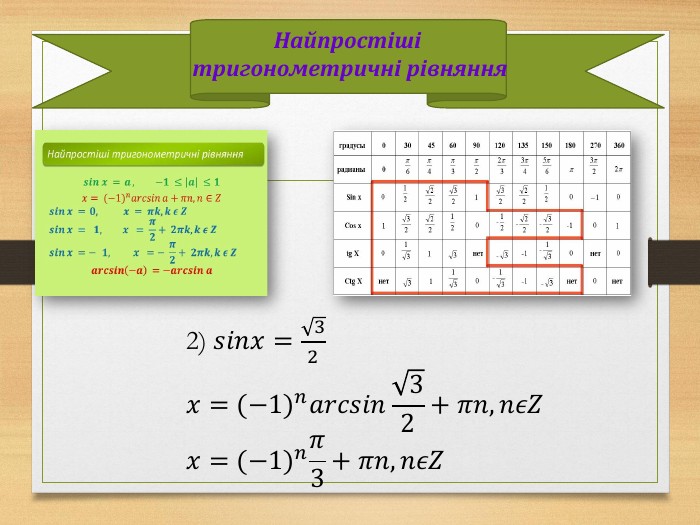
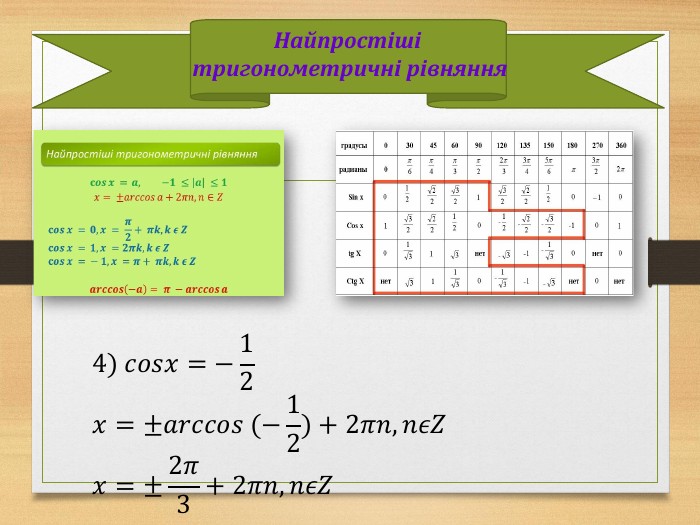
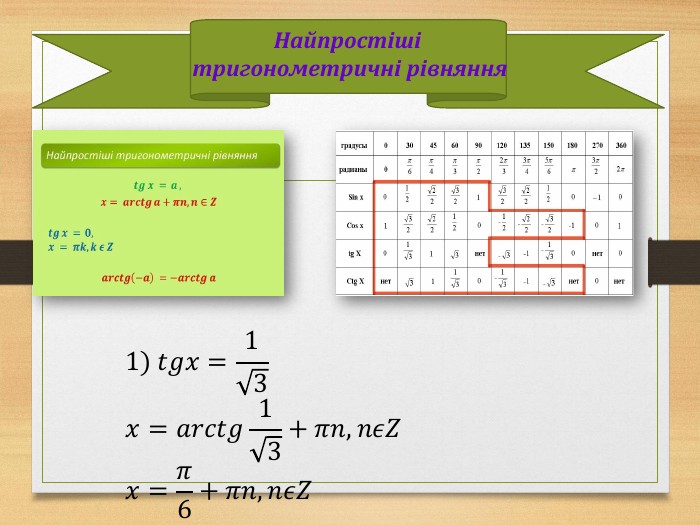
Виведення загальної формули коренів найпростішого рівняння

МІНІСТЕРСТВО ОСВІТИ І НАУКИ УКРАЇНИНАЦІОНАЛЬНИЙ ПЕДАГОГІЧНИЙ УНІВЕРСИТЕТ ІМЕНІ М. П. ДРАГОМАНОВАФАКУЛЬТЕТ МАТЕМАТИКИ, ІНФОРМАТИКИ ТА ФІЗИКИЗаочне відділення. Завдання 2 Тема «Виведення загальної формули коренів найпростішого рівняння»Виконала:студентка 1 курсу групи 1ммз. СО Мігульова Ольга. Викладач Лук»янова С. М

Найпростіші тригонометричні рівняння𝑠𝑖𝑛𝑥=𝑎 𝑐𝑜𝑠𝑥=𝑎 𝑡𝑔𝑥=𝑎 𝑠𝑖𝑛𝑥=𝑎 𝑐𝑡𝑔𝑥=𝑎 

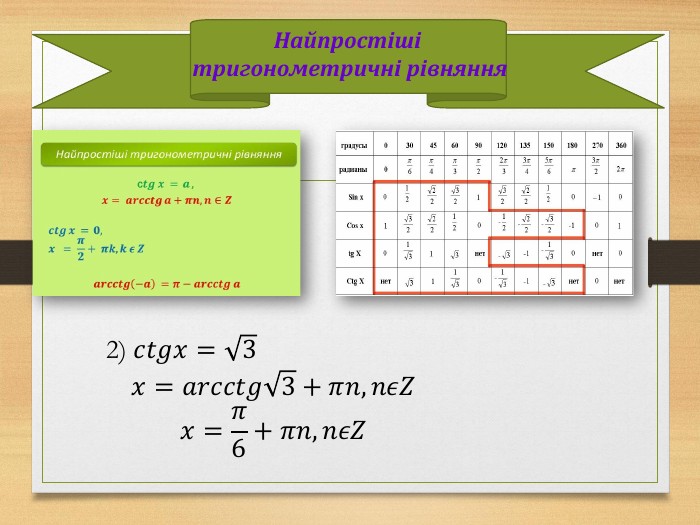
Курс алгебри і початків аналізу передбачає навчити учнів розв'язувати трансцендентні рівняння й нерівності (тригонометричні, показникові, логарифмічні) та ірраціональні рівняння й нерівності. Це пов'язується з розглядом властивостей відповідних функцій. Відомо, що не існує загального способу розв'язування трансцендентних рівнянь і нерівностей. Проте за умов середньої школи доцільно ознайомити учнів зі способами розв'язування найпростіших та окремих видів таких рів­нянь і нерівностей, до яких здебільшого зводиться розв'язування складніших. Практика свідчить, що доцільно звести в систему окремі види рівнянь і нерівностей за способами їх розв'язування. Відповідно до чинної програми учні мають уміти розв'язувати найпростіші тригонометричні рівняння (sin х = a, cos x = a, tg х = а) та деякі нескладні види тригонометричних рівнянь, які зводяться до найпростіших.

Тригонометрія традиційно є одним із найважливіших складових частин шкільного курсу математики. І цей курс передбачає завдання, вирішення яких, зазвичай, можна, пройшовши цілеспрямовану спеціальну підготовку. В давнину тригонометрія виникла у зв'язку з потребами астрономії, і будівельної справи, тобто носила чисто геометричний характер і представляла головним чином «вирахування хорд». З часом в неї почали вкрапляться деякі аналітичні моменти. У першій половині VXIII століття відбувся різкий перелом, після чого тригонометрія прийняла новий напрямок і змістилася у бік математичного аналізу. Саме в цей час тригонометричні залежності стали розглядатися як функції. Тригонометричні рівняння одна з найскладніших тем у курсі математики. Тригонометричні рівняння виникають при вирішенні завдань по планіметрії, стереометрії, астрономії, фізики і в інших областях.

Свого часу велася запекла дискусія з приводу означення поняття тригонометричне рівняння. Тригонометричним пропонували називати: рівняння, в якому змінна входить лише під знак тригонометричної функції (в такому разі рівняння виду sin х+х=0 не належить до тригонометричних; його пропонували називати трансцендентним); рівняння, в якому змінна входить під знак тригонометричної функції. З цього приводу слід погодитись з думкою С. І. Новосьолова, який вважав, що розходження в означеннях тригонометричного рівняння не є принциповими. Важливо одне – немає загального методу розв'язування тригонометричних рівнянь. Слід наголосити на принциповій відмінності тригонометричних рівнянь від алгеб­раїчних: тригонометричні рівняння, в яких змінна входить лише під знак тригонометричної функції, або зовсім не мають розв'язків, або мають їх безліч. Це пов'язано з властивістю періодичності тригонометричних функцій.

У курсі математики тригонометричні рівняння розглядаються на множині дійсних чисел. При розв’язанні тригонометричних рівнянь спочатку потрібно визначити область допустимих значень невідомого, враховуючи, що функції cos x i sin x визначені при всіх дійсних значеннях x, функція tg x визначена при х≠𝝅𝟐𝒌+𝟏𝟐, де k ∈ Z, і функція ctg x визначена при, х≠𝝅𝒌,  k∈Z. Загального методу розв’язання тригонометричних рівнянь не існує, і пошук розв’язання в кожному конкретному випадку потребує певної майстерності у виконанні тригонометричних перетворень, знання тригонометричних формул. Потрібно зазначити, що при розв’язанні найпростіших тригонометричних рівнянь запис розв’язків має однозначну форму. У більш складних прикладах форма запису множини розв’язків неоднозначна, але ідентичність різних форм запису завжди можна довести за допомогою тотожних перетворень. Різна форма запису пояснюється різними методами, за допомогою яких розв’язується дана задача. Розв’язування різних типів тригонометричних рівнянь в основному зводиться до розв’язання найпростіших тригонометричних рівнянь. Розв’язати найпростіше тригонометричне рівняння — означає знайти множину всіх кутів, що мають дане значення тригонометричної функції 

𝑎𝑟𝑐𝑠𝑖𝑛12=𝜋6 𝑎𝑟𝑐𝑠𝑖𝑛22=𝜋4 𝑎𝑟𝑐𝑠𝑖𝑛32=𝜋3 𝑎𝑟𝑐𝑐𝑜𝑠12=𝜋3 𝑎𝑟𝑐𝑐𝑜𝑠22=𝜋4 𝑎𝑟𝑐𝑐𝑜𝑠32=𝜋3 𝑎𝑟𝑐𝑡𝑔13=𝜋6 𝑎𝑟𝑐𝑡𝑔1=𝜋4 𝑎𝑟𝑐𝑡𝑔3=𝜋3 

Найпростіші тригонометричні рівняння1) 𝑠𝑖𝑛𝑥=12𝑥=(−1)𝑛𝑎𝑟𝑐𝑠𝑖𝑛12+𝜋𝑛, 𝑛𝜖𝑍𝑥=(−1)𝑛𝜋6+𝜋𝑛, 𝑛𝜖𝑍 

Найпростіші тригонометричні рівняння2) 𝑠𝑖𝑛𝑥=32𝑥=(−1)𝑛𝑎𝑟𝑐𝑠𝑖𝑛32+𝜋𝑛, 𝑛𝜖𝑍𝑥=(−1)𝑛𝜋3+𝜋𝑛, 𝑛𝜖𝑍 

Найпростіші тригонометричні рівняння3) 𝑠𝑖𝑛𝑥=22𝑥=(−1)𝑛𝑎𝑟𝑐𝑠𝑖𝑛22+𝜋𝑛, 𝑛𝜖𝑍𝑥=(−1)𝑛𝜋4+𝜋𝑛, 𝑛𝜖𝑍 

Найпростіші тригонометричні рівняння4) 𝑠𝑖𝑛𝑥=−12𝑥=(−1)𝑛arcsin(−12)+𝜋𝑛, 𝑛𝜖𝑍𝑥=−1𝑛(−𝜋6)+𝜋𝑛, 𝑛𝜖𝑍 𝑥=(−1)𝑛+1𝜋6+𝜋𝑛, 𝑛𝜖𝑍 

Найпростіші тригонометричні рівняння1) 𝑐𝑜𝑠𝑥=12𝑥=±𝑎𝑟𝑐𝑐𝑜𝑠12+2𝜋𝑛, 𝑛𝜖𝑍𝑥=±𝜋3+2𝜋𝑛, 𝑛𝜖𝑍 

Найпростіші тригонометричні рівняння2) 𝑐𝑜𝑠𝑥=32𝑥=±𝑎𝑟𝑐𝑐𝑜𝑠32+2𝜋𝑛, 𝑛𝜖𝑍𝑥=±𝜋6+2𝜋𝑛, 𝑛𝜖𝑍 

Найпростіші тригонометричні рівняння3) 𝑐𝑜𝑠𝑥=22𝑥=±𝑎𝑟𝑐𝑐𝑜𝑠22+2𝜋𝑛, 𝑛𝜖𝑍𝑥=±𝜋4+2𝜋𝑛, 𝑛𝜖𝑍 

Найпростіші тригонометричні рівняння4) 𝑐𝑜𝑠𝑥=−12𝑥=±𝑎𝑟𝑐𝑐𝑜𝑠 (−12)+2𝜋𝑛, 𝑛𝜖𝑍𝑥=±2𝜋3+2𝜋𝑛, 𝑛𝜖𝑍 

Найпростіші тригонометричні рівняння1) 𝑡𝑔𝑥=13𝑥=𝑎𝑟𝑐𝑡𝑔13+𝜋𝑛, 𝑛𝜖𝑍𝑥=𝜋6+𝜋𝑛, 𝑛𝜖𝑍 

Найпростіші тригонометричні рівняння2) 𝑡𝑔𝑥=3𝑥=𝑎𝑟𝑐𝑡𝑔3+𝜋𝑛, 𝑛𝜖𝑍𝑥=𝜋3+𝜋𝑛, 𝑛𝜖𝑍 

Найпростіші тригонометричні рівняння3) 𝑡𝑔𝑥=1𝑥=𝑎𝑟𝑐𝑡𝑔1+𝜋𝑛, 𝑛𝜖𝑍𝑥=𝜋4+𝜋𝑛, 𝑛𝜖𝑍 

Найпростіші тригонометричні рівняння4) 𝑡𝑔𝑥=−3𝑥=𝑎𝑟𝑐𝑡𝑔(−3)+𝜋𝑛, 𝑛𝜖𝑍𝑥=−𝜋3+𝜋𝑛, 𝑛𝜖𝑍 

Найпростіші тригонометричні рівняння1)𝑐𝑡𝑔𝑥=13𝑥=𝑎𝑟𝑐𝑐𝑡𝑔13+𝜋𝑛, 𝑛𝜖𝑍𝑥=𝜋3+𝜋𝑛, 𝑛𝜖𝑍 

Найпростіші тригонометричні рівняння2) 𝑐𝑡𝑔𝑥=3𝑥=𝑎𝑟𝑐𝑐𝑡𝑔3+𝜋𝑛, 𝑛𝜖𝑍𝑥=𝜋6+𝜋𝑛, 𝑛𝜖𝑍 

Найпростіші тригонометричні рівняння3) 𝑐𝑡𝑔𝑥=1𝑥=𝑎𝑟𝑐𝑐𝑡𝑔1+𝜋𝑛, 𝑛𝜖𝑍𝑥=𝜋4+𝜋𝑛, 𝑛𝜖𝑍 

Найпростіші тригонометричні рівняння4) 𝑐𝑡𝑔𝑥=−3𝑥=𝑎𝑟𝑐𝑡𝑔(−3)+𝜋𝑛, 𝑛𝜖𝑍𝑥=5𝜋6+𝜋𝑛, 𝑛𝜖𝑍 

Найпростіші тригонометричні рівняння1)  𝑐𝑜𝑠2𝑥=222𝑥=±𝑎𝑟𝑐𝑐𝑜𝑠22+2𝜋𝑛, 𝑛𝜖𝑍2𝑥=±𝜋4+2𝜋𝑛, 𝑛𝜖𝑍𝑥=±𝜋8+𝜋𝑛, 𝑛𝜖𝑍 

Найпростіші тригонометричні рівняння2) sin(𝑥+𝜋2)=12𝑥+𝜋2=(−1)𝑛𝑎𝑟𝑐𝑠𝑖𝑛12+𝜋𝑛, 𝑛𝜖𝑍𝑥=(−1)𝑛𝜋6−𝜋2+𝜋𝑛, 𝑛𝜖𝑍 

Найпростіші тригонометричні рівняння3)3𝑐𝑡𝑔𝑥=1𝑐𝑡𝑔𝑥=13𝑥=𝑎𝑟𝑐𝑐𝑡𝑔13+𝜋𝑛, 𝑛𝜖𝑍𝑥=𝜋3+𝜋𝑛, 𝑛𝜖𝑍 

Найпростіші тригонометричні рівняння4) 𝑡𝑔(2𝑥−𝜋4)=12𝑥−𝜋4=𝑎𝑟𝑐𝑡𝑔1+𝜋𝑛, 𝑛𝜖𝑍2𝑥−𝜋4=𝜋4+𝜋𝑛, 𝑛𝜖𝑍2𝑥=𝜋4+𝜋4+𝜋𝑛, 𝑛𝜖𝑍2𝑥=𝜋2+𝜋𝑛, 𝑛𝜖𝑍𝑥=𝜋4+𝜋𝑛2, 𝑛𝜖𝑍 

Математика 10 клас А. Г. Мерзляк, Д. А. Номіровський, В. Б. Полонський, М. С. Якір 2018. Алгебра і початки аналізу та геометрія. Математика 10 клас О. С. Істер 2018. Алгебра і початки аналізу та геометрія. Математика 10 клас Г. П. Бевз, В. Г. Бевз 2011. Рівень стандарту. Мірошин В. Відбір коренів у тригонометричних рівняннях // Математика. Список використаних джерел