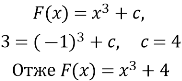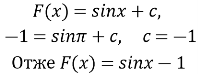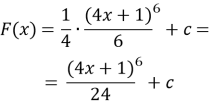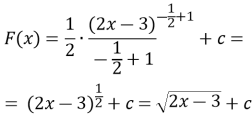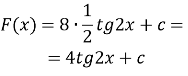Визначений інтеграл. Фізичний та геометричний зміст
Тема заняття: Визначений інтеграл. Його фізичний та геометричний зміст.
Методична мета заняття: застосування інноваційних технологій при вивченні математики з використанням елементів самостійної роботи; розвиток творчої складової в процесі формування вмінь та навичок студентів, застосування активних форм і методів виховання особистості компетентного студента та майбутнього спеціаліста.
Мета.
Навчальна: Поглибити й розширити знання студентів про визначений інтеграл; закріпити навички знаходити визначений інтеграл, показати його місце і значення при розв’язуванні задач фізичного, геометричного змісту; учити бачити єдину математичну модель у різних ситуаціях, складати її в нестандартних умовах.
Розвиваюча: Вчити студентів досліджувати й оцінювати соціальні явища засобами математики; бачити необхідність планування майбутнього; допомогти сформувати особисте ставлення до діяльності, яка вимагає математичних знань.
Виховна: Виховувати математичну культуру, вміння правильно застосовувати математичну символіку; виховувати інтерес до дисципліни розкриваючи її велике значення для розвитку різних галузей наук та повсякденного життя.
Міжпредметні зв’язки.
Забезпечувані. Фізика. Знаходження шляху, пройденим тілом.
Математика. Інтегральне числення (вища математика),
геометрія – обчислення площ фігур.
Функції:
Теоретична - Знати: поняття криволінійної трапеції, її площі; поняття
визначеного інтеграла, його геометричний та фізичний зміст.
Практична - Вміти: обчислювати визначені інтеграли, знаходити площі криволінійних трапецій, розв’язувати задачі фізичного змісту з використанням визначених інтегралів.
Вид заняття. Комбіноване заняття.
Забезпечення заняття.
1. Література. О. Істер. Математика 11 клас.
2. Наочні посібники. Таблиці “Основні формули інтегрування” та «Формули з алгебри та геометрії за курс повної загальної середньої освіти»
3. Роздаткові матеріали. Опорні конспекти “Основні формули інтегрування”. Варіанти завдань для самостійної роботи.
4. Комп’ютер, проектор.
Хід заняття
І. Перевірка відвідування і матеріальної готовності до заняття
(Метод: психолого – педагогічної підтримки роботи студентів на занятті, рефлексія 2 хв)
1.1 Встановлення психолого – педагогічного контакту з аудиторією студентів.
1.2 Викладач перевіряє готовність студентів до заняття, налаштовує їх на роботу.
ІІ. Перевірка домашнього завдання.
Викладач демонструє правильне виконання домашнього завдання на слайді, студенти звіряють власні виконані завдання.
п.9 № 9.14, 9.20, 9,24
![]()
|
|
|
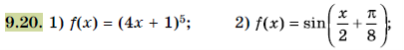
|
|
|
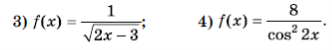
|
|
|

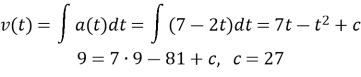
![]() шукане рівняння швидкості м.т.
шукане рівняння швидкості м.т.
ІІІ. Перевірка раніше засвоєних знань та елементів практичних навичок.
( методи – метод „ Мікрофон ", пояснювально – ілюстративний; форма роботи - презентація, діалог, тестування)
А зараз, відповідаючи на питання, ми налаштуємося на розгляд більш складних проблем.
1. Як називають знаходження функції за її похідною? (операцією інтегрування, що є оберненою до операції диференціювання).
2. Що таке первісна? (функція ![]() називають первісною для функції
називають первісною для функції ![]() на заданому проміжку, якщо для всіх х з цього проміжку виконується рівність
на заданому проміжку, якщо для всіх х з цього проміжку виконується рівність ![]() ).
).
3. Що таке інтеграл? (інтеграл це сукупність первісних)
4. Назвіть, будь ласка, три правила знаходження первісної (правила інтегрування).
(![]()
![]() .
.
5. Застосування первісних у фізиці. (можна відновити закон руху точки за даною в кожен момент швидкості, ![]() ).
).
6. Співставте рівнянням кривих відповідні графіки функцій за малюнком
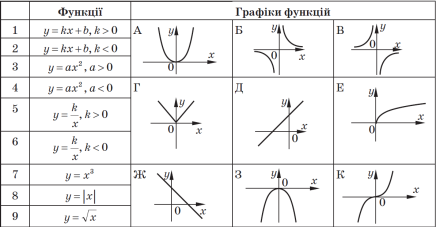
А зараз ми ще раз звернемося до інтегралів й перевіримо, як ви вмієте знаходити інтеграл степеневої функції.
Вставте пропущені символи, щоб рівність була правильною.

Після виконання самостійної роботи студенти обмінюються завданнями та перевіряють правильність виконання самостійної роботи, звіряючи написане в зошиті з правильними відповідями на слайді (кожне завдання 2б, виставляють оцінки).

IV. Мотивація навчання та актуалізація опорних знань студентів
(методи: бесіда, навіювання, переконання)
Наша мета сьогодні – не тільки закріпити вміння і навички знаходження невизначеного інтегралу але й застосування та властивості визначеного інтегралу.
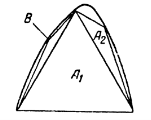
 Інтегральне числення і само поняття інтеграла виникли з потреб обчислення площ плоских фігур і об’ємів довільних тіл. Ідеї інтегрального числення беруть свій початок у роботах стародавніх математиків.
Інтегральне числення і само поняття інтеграла виникли з потреб обчислення площ плоских фігур і об’ємів довільних тіл. Ідеї інтегрального числення беруть свій початок у роботах стародавніх математиків.
Першим відомим методом для розрахунку інтегралів був метод вичерпування Евдокса Кнідського (приблизно 370 років до н.е.), який намагався знайти площі та об'єми різноманітних фігур і для цього розривав їх на величезну кількість частин, для яких площа і об'єм вже відомі (знаходження площі фігури В).
 Цей метод розвинув Архімед, який стверджував, що найпершим другом в його житті була математика, і використав метод Евдокса для розрахунку площ парабол і наближених обчислень площ частин круга. Одного разу Архімед повернувся з риболовлі і вирішив визначити найбільш точно площу поверхні риби. Архімед розбив поверхню риби на прямокутники і знайшов їх площі, причому чим більшою була кількість прямокутників, тим точнішим було значення площі.
Цей метод розвинув Архімед, який стверджував, що найпершим другом в його житті була математика, і використав метод Евдокса для розрахунку площ парабол і наближених обчислень площ частин круга. Одного разу Архімед повернувся з риболовлі і вирішив визначити найбільш точно площу поверхні риби. Архімед розбив поверхню риби на прямокутники і знайшов їх площі, причому чим більшою була кількість прямокутників, тим точнішим було значення площі.
Символ інтеграла ввів Г. Лейбніц 1675р. Слово інтеграл придумав Й.Бернуллі. Межі інтегрування вказав Л.Ейлер. Сьогодні на занятті ми введемо з вами формулу для обчислення визначеного інтегралу, яку називають формулою Ньютона –Лейбниця, до речі в тому вигляді, що ми будемо використовувати дану формулу, ні Ньютон ,ні Лейбниць її не використовували але це правило вони знали. Відкриття Ньютона і Лейбніца, які працювали незалежно один від одного, зробило переворот в математиці. Якщо раніше вона була доступна лише вузькому кругу фахівців, які розв’язували кожне окреме завдання придуманими ними методами, то після створення алгоритму диференціального і інтегрального числення, застосованого до широкого кола задач, математика стала інструментом в руках дослідників, які не володіють достатньо глибокими математичними знаннями.
Анрі Пуанкаре, французький математик, сказав: «Математика є спосіб називати різні речі одним ім’ям». Можливість розвивати ці уміння ви й матимете сьогодні, розв’язуючи задачі, пов’язані з геометрією та фізичними явищами. І ви матимете чудову нагоду розвинути і закріпити навички знаходити визначений інтеграл, застосовувати його при розв’язуванні практичних задач.
V. Вивчення нового матеріалу і його первинне осмислення
(розповідь з елементами бесіди, пояснення, тренувальні вправи, інструктування, ілюстрація)
Робота з підручником, стр. 91. Розглянемо геометричний та фізичний зміст визначеного інтегралу, для цього складемо невеличку таблицю
|
геометричний зміст визнач. інт. |
фізичний зміст визнач. інт. |
|
|
|

Кожна криволінійна трапеція моє певну площу, яка знаходиться за теоремою про площу криволінійної трапеції, доведення якої ви розглянете самостійно.
Площа криволінійної трапеції знаходиться за формулою S=F(a)-F(b), де F(x) це первісна від функції ![]()

Маємо геометричний зміст визначеного інтегралу (напишемо в таблицю):

Приклад: обчисліть площу фігури, зображену на малюнку
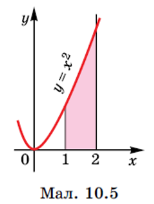 Розв’язання: так як криволінійну трапецію обмежує з одного боку крива
Розв’язання: так як криволінійну трапецію обмежує з одного боку крива ![]() , а з інших боків прямі х=1(a), х=2(b) та у=0 і S=F(b)-F(a), то знайдемо первісну функції і використаємо дану формулу
, а з інших боків прямі х=1(a), х=2(b) та у=0 і S=F(b)-F(a), то знайдемо первісну функції і використаємо дану формулу
F(x)=![]() ,
,
![]()
Розглянемо іншу задачу фізичного змісту, що приводить до поняття визначеного інтегралу стр 93. 
Маємо фізичний зміст визначеного інтегралу (напишемо в таблицю)::

Приклад: Автомобіль BMW рухається зі швидкістю, що описується законом ![]() (м/с) приймає участь у гонках. Сусідній автомобіль Audi за перші 2 секунди після початку руху проїде 15 м. Який з автомобілів буде попереду після старту?
(м/с) приймає участь у гонках. Сусідній автомобіль Audi за перші 2 секунди після початку руху проїде 15 м. Який з автомобілів буде попереду після старту?
Розв’язання: так як ![]() і
і ![]() є первісною для
є первісною для ![]() маємо
маємо
![]()
![]() проїде BMW за перші 2с, отже Audi буде попереду.
проїде BMW за перші 2с, отже Audi буде попереду.
Очікувані записи в таблиці:
|
геометричний зміст визнач. інт. |
фізичний зміст визнач. інт. |
|
рівна площа S=F(b)-F(a) Приклад:
F(x)=
|
S=F(b)-F(a) Приклад:
Автомобіль BMW рухається зі швидкістю, що описується законом
Розв’язання: так як
|
Отже для обчислення визначеного інтегралу використовується
формула Ньютона-Лейбниця
![]() ,
,
де b - верхня границя, a - нижня границя (a<b), ![]() - первісна для f(x),
- первісна для f(x), ![]() .
.
VІ. Узагальнення та систематизація знань (метод корекції знань, формування навичок, предметних компетенцій, розв’язування задач)
п. 10 стр 97 № 10.2, 10.3, 10.5, 10.7, 10.9
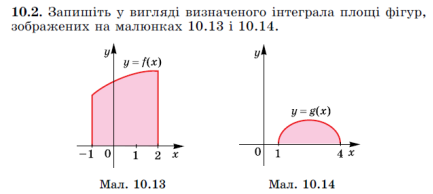
![]()
![]()
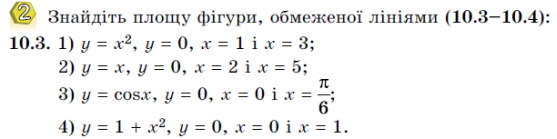
Розв’язання:
1) ![]()
![]()
![]()
![]()
![]()
функція первісна значення в точках
2) ![]()
3) ![]()
4) ![]()

Розв’язання:
1) Графіком є кубічна парабола, у=0 (це вісь ОХ) і чітко видно, що криволінійна трапеція починається в точці х=0 і закінчується х=2
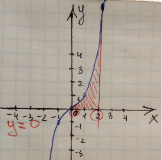
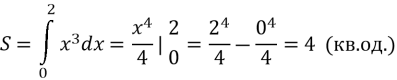
2) Графіком функції є парабола y=x2, вітки вниз, що переміщена по вісі OY вгору на 4 одиниці, у=0 (це вісь ОХ) і чітко видно, що криволінійна трапеція починається в точці х=-2 і закінчується х=2 (координати перетину параболи з віссю ОХ)
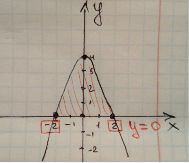
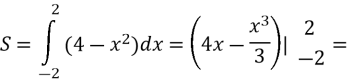
![]() =
=
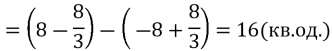
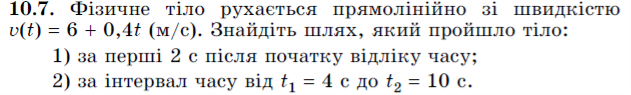
Розв’язання:
1) В даному випадку маємо дві точки: х=0 (початок руху) і х=2 (час руху точки)
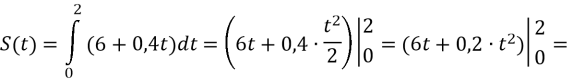
![]()
2) Знайдемо відстань, що пройде точка за заданий період
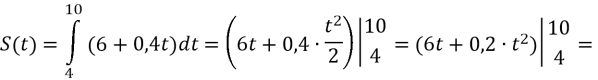
![]()
Розв’язання:
1) Графіком є парабола, y=x2, вітки вгору, що зміщена по вісі OY вниз на 1.
![]()
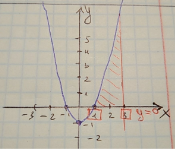
![]()
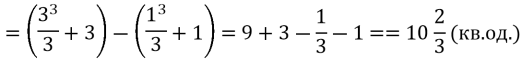
2) Для побудови цього графіку потрібно знайти вершину параболи, та точки перетину з осями координат.
Вершина: ![]()
![]()
![]()
![]()
![]()
VІІ. Підсумок заняття
(метод: виконання тестових завдань )
Розв’язування тестових завдань «Перевір себе»:
1. За якою з наведених формул визначається площа заданої фігури?
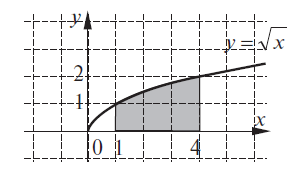
1. ![]()
2. ![]()
3. ![]()
4. ![]()
2. Визначте фігуру. Площа якої знаходиться за формулою ![]() ?
?
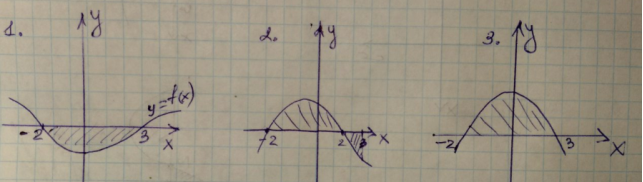
3. Знайдіть в яких записах є помилка.
1. 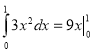 2.
2. 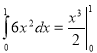
3. 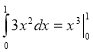 4.
4. 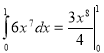 .
.
4. За якою з наведених формул обчислюється відстань, що проходить матеріальна точка з 2с по 5с, швидкість якої змінюється за законом
![]() ?
?
1. ![]() 2.
2. ![]()
3. ![]() 4.
4. ![]()
5. Обчисліть визначений інтеграл ![]()
1. =5 2. =-5 3. =15 4. =-15
Ми зійшли на вершину гори, долаючи труднощі, виявляючи нетерпіння, наполегливість. На шляху нам зустрічалися фігури, площі яких ще вчора ми не вміли знаходити та фізичні явища, для розуміння і пояснення яких необхідні математичні знання.
Прочитайте фразу, написану на слайді: „Забути не можна пам’ятати!”
Від того, у якому місці ви поставите кому, матимете два варіанти: «Забути, не можна пам’ятати!» або «Забути не можна, пам’ятати!»
На якому варіанті ви зупинитесь? Чи потрібні вам знання з математики в майбутньому?
VІІІ. Постановка роз’яснення домашнього завдання
Вивчити теорію, вміти використовувати формулу Ньютона-Лейбниця при розв’язування задач геометричного та фізичного змісту. Підготовитись до самостійної роботи.
П. 10 № 10.4, 10.6, 10.8, 10.10
1


про публікацію авторської розробки
Додати розробку