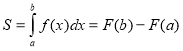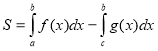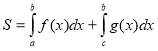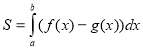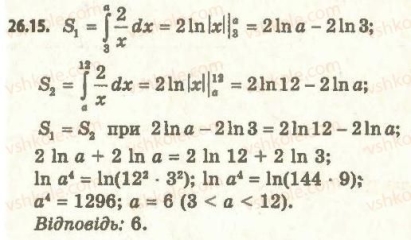Визначений інтеграл та його застосування

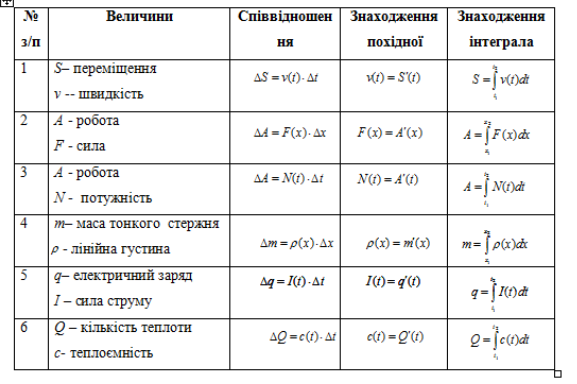
ЗЗСО І – ІІІ ступенів с. Погреби

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Вчитель математики Сергієнко Л.І.

 

 

 

2022р.
Тема уроку: Визначений інтеграл та його застосування.

 

Мета уроку

Освітня: узагальнити та систематизувати знання учнів про визначений інтеграл; вдосконалювати вміння і навички обчислення визначених інтегралів, формувати математичну грамотність: уміння застосовувати математичні (числові та геометричні) методи для розв’язання прикладних завдань у різних сферах діяльності, здатність до розуміння і використання простих математичних моделей при розв’язуванні задач фізичного, економічного, геометричного змісту.

Розвиваюча: розвивати навички самостійного мислення, інтелектуальні навики (аналіз, синтез, порівняння, співставлення), увагу, пам’ять.

Виховна: виховувати вміння раціонально використовувати робочий час, математичну культуру учнів, підвищувати інтерес до предмету.

Тип уроку: урок узагальнення та систематизації знань, умінь та навичок.

 

Той, хто серйозно прямує до пізнання істини,

не повинен займатися якоюсь однією наукою,

бо всі вони взаємозв’язані

Рене Декарт

Обладнання: мультимедійна дошка; картки-пам’ятки для учнів;

підручник: Алгебра. 11 клас: підручн. для загальноосвіт. навчальн. закладів: академ. Рівень, проф. рівень/ А. Г. Мерзляк, Д. А. Номіровський, В. Б. Полонський, М. С. Якір. – Х.: Гімназія, 2011. – 431 с.: іл.

І. Організаційний момент.

ІІІ. Перевірка домашнього завдання.

ІV. Узагальнення і систематизація знань учнів про визначений інтеграл та його застосування.

V. Підведення підсумків уроку

VІ. Домашнє завдання.

Хід уроку

 

І. Організаційний момент.

Привітання, повідомлення теми (Слайд 1).

ІІ. Перевірка домашнього завдання.

1. Наявність домашнього завдання перевіряється в усіх учнів. Вибірково – правильність.
2. Відповіді на питання, що виникли в учнів при виконанні домашнього завдання.
3. Інтерактивна гра «Знайди та виправ помилки».

Вправи

1)+ 4² – 4³ – (-4 + 1 – 1) =    = -1 + 16 - 64 +4 = - 45;

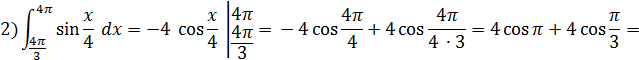
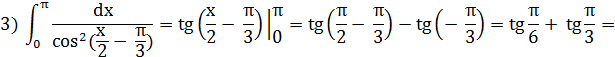
4) ;

5) ;

;

;

.

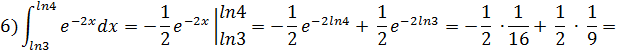
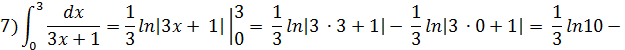
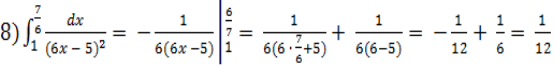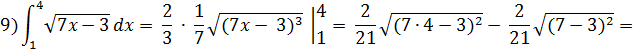
(Помилки в 3 та 5 завданні)

ІІІ. Актуалізація опорних знань.

І. Заповнити пропуски в тексті:

1. Функція __ називається первісною функції ______ на деякому проміжку, якщо для  всіх  х  із цього проміжку виконується рівність: ___________________________ .
2. Нехай функція f має на деякому проміжку первісну. Сукупність усіх первісних для функції f(x) на проміжку називається _________________ ___________ цієї функції і позначають _________. Функцію __________ називають __________________ .
3.  Нехай функція F(x) є первісною для f(x) на деякому проміжку. Тоді для довільної _____________ функція _____________ також є первісною для функції __________ .
4. Нехай функція __ є первісною для ___ на деякому проміжку. Тоді будь-яка первісна для функції f(x) цьому проміжку може бути записана у вигляді  F(x) + C, де С – деяка стала (число).
5. Дія обернена до диференціювання називається _____________________.

ІІ. Таблиця первісних.

 

Функція f	Загальний вигляд первісних функції f
k (стала)	kx + C
xn,, n ≠ -1	+ С
	ln + C
	+ С
	2 + С
sin x	-cos x + C
cos x	sin x + C
	tg x + C
	-ctg x + C
ax
ex	ex + C

 

ІІІ. Правила інтегрування.

 

ІV. Інтеграли в історії (Слайди 6-9)

 

ІV. Узагальнення і систематизація знань учнів про визначений інтеграл та його застосування.

 

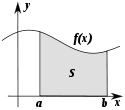
1.     Обчислення площ плоских фігур.

 

	Площа криволінійної трапеції
	Обчислення площ

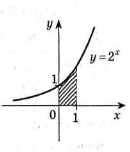
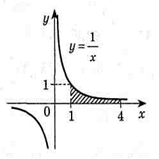
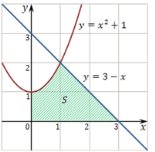
2.     Запишіть за допомогою інтеграла площу фігури зображеної на рисунку

 

 

3) Установити відповідність між визначеними інтегралами (1- 4) та їх значеннями (А –Д).

 

1)

2)

3)

4)

	А	Б	В	Г	Д			А	0,1
1								Б	2
2								В	3,75
3								Г	0
4								Д	4

 

4) Завдання 31 (ЗНО 2018)

Задано функції  f(x) = x³ і g(x) = 4|x|.

1. Побудувати графік функції f.

2. Побудувати графік функції g.

3. Визначте абсциси перетину графіків f і g.

4. Обчисліть площу фігури, обмеженої графіками функцій f і g.

 

Завдання 26.12. При якому додатному значенні а визначений інтеграл
набуває найбільшого значення?

Розв’язання:

 

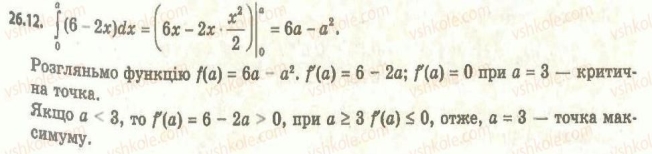
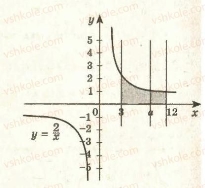
Завдання 26.15. При якому значені а пряма х = а розбиває фігуру, обмежену графіком функції y=  2/x і прямими у = 0, х = 3, х = 12, на дві рівновеликі фігури?

 

 

5.     Інтеграл у фізиці, механіці і економіці. (Слайди 16 – 32)

 Задача 1. Знайти кількість електрики, яка проходить через поперечний переріз провідника за 20 с, якщо сила струму змінюється за законом                                 І(t) = 2t + 1 (A).

Розв’язання: Кількість електрики може бути обчислена формулою:

Тоді: t₁ = 0c, t₂ = 20c

 

q =

Задача 2. Тіло рухається прямолінійно зі швидкістю v(t) = 18t – 3t²  (м/с).

 Обчисліть шлях, який пройшло тіло за інтервал часу від 2 с до 5 с.

Розв’язання: Відстань обчислюється за формулою:

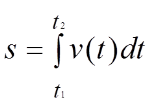
Підставимо дані з умови задачі:

S =

= 225 – 125 – 36 + 8 = 72 (м)

Знаходження капіталу за відомими інвестиціями.

Розглянемо задачу знаходження капіталу (основних фондів) за відомими частими інвестиціями. Чисті інвестиції (капіталовкладення) - це загальні інвестиції, які були зроблені за певний проміжок часу, за винятком інвестицій на відшкодування основних фондів (капіталу), які виходять з ладу. Таким чином, за одиницю часу капітал збільшується на суму чистих інвестицій.

Якщо капітал розглядати як функцію часу  K(t), а чисті інвестиції, відповідно, як  f(t), то викладене вище можна записати у вигляді:

.

Часто вимагається знайти приріст капіталу за період з моменту часу t₁ до t₂, тобто величину ∆K = K(t₂) – K(t₁).

Враховуючи, що K(t) - первісна для функції f(t), маємо:

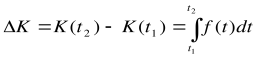
 Задача 3. Чисті інвестиції задано функцією f(t) = 7000√t. Визначити приріст капіталу за три роки.

Розв’язок. Скористаємося формулою для обчислення приросту капіталу ∆K, нехай t₁ = 0; t₂ = 3.

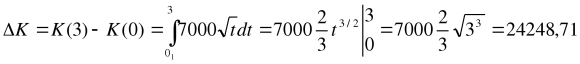
ІV. Підведення підсумків уроку.

Рефлексія (кросворд)

С

У

М

А

Н

Ь

Ю

Т

О

Н

Л

Е

Й

Б

Н

І

Ц

К

Р

И

В

О

Л

І

Н

І

Й

Н

А

П

І

Д

І

Н

Т

Е

Г

Р

А

Л

Ь

Н

А

Д

И

Ф

Е

Р

Е

Н

Ц

І

А

Л

І

Н

Т

Е

Г

Р

У

В

А

Н

Н

Я

 Питання:

1. Першу букву якого слова нагадує знак інтеграла? (Сума)

2. Хто з відомих математиків-фізиків дослідив фізичний зміст інтеграла? (Ньютон)

3. Хто з відомих математиків дослідив геометричний зміст інтеграла? (Лейбніц)

4. Як називається трапеція, площу якої  ми знаходимо за допомогою визначеного інтеграла? (Криволінійна)

5. Як називається функція, яка стоїть під знаком інтеграла?       (Підінтегральна)

6. Як називається множник dх у підінтегральному виразі? (Диференціал)

7. Як називається операція обернена до операції диференціювання? (Інтегрування)

VІ. Домашнє завдання.

Підручник §25, 26  – повторити,  виконати №26.14, 26.16, завдання № 31 (ЗНО 2017), додаткове завдання: пошукова робота «Прикладні задачі з використанням визначеного інтеграла».