Властивості арифметичного квадратного кореня

Урок № 39

Тема уроку: Властивості арифметичного квадратного коріня (із добутку, дробу та степеня.  Добуток і частка квадратних коренів

Мета уроку: сформувати в учнів знання про властивості арифметичного квадратного кореня, сформульовані у вигляді теорем , вміння застосовувати вивчені властивості для перетворення квадратного кореня з добутку або дробу на добуток чи відношення квадратних коренів і для перетворення добутку або відношення квадратних коренів на квадратний корінь із добутку або дробу; розвивати увагу, логічне мислення, пам’ять; виховувати акуратність, працелюбність, дисциплінованість.

Обладнання: підручник, роздавальний матеріал

Тип уроку: урок засвоєння нових знань.

 I. Організаційний етап

▪ Привітання

▪ Перевірка присутності учнів

▪ Перевірка готовності учнів та кабінету до уроку

II. Перевірка домашнього завдання

▪ Робота в парах

Знайдіть значення виразу: а) ; б) ; в) ; г) ;   Відповіді      а) 0,3;       б) 7;         в) 6,2;          г) .

1. Розв’яжіть рівняння .

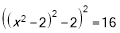Розв’язання

; ; або ; — отже, рівняння не має коренів.

або ;

або .

Відповідь: ; .

2. За яких значень a рівняння має один корінь?

Розв’язання

Рівняння має один корінь, якщо ; ; або ; ; .

Відповідь: якщо або , то рівняння має один корінь.

III. Формулювання мети й завдань уроку, мотивація навчальної діяльності

▪ Оголошення теми уроку

▪ Формулювання разом з учнями мети й завдань уроку

▪ Мотивація навчальної діяльності

Знайдемо значення виразу . Це нескладно зробити, і, як ви розумієте, отримаємо . Знайдіть значення виразів , , . Як бачимо, тут нас спіткають труднощі, і знання тільки означення арифметичного квадратного кореня недостатньо, тому треба поговорити про властивості арифметичного квадратного кореня, застосування яких дозволить нам обчислити значення виразів, що мають вигляд арифметичного квадратного кореня з добутку, частки, степеня, добутку коренів і частки коренів.

IV. Актуалізація опорних знань

▪ Бліц-опитування за технологією «Мікрофон»

1. Обчисліть:  а) ;     б) ;     в) ;     г) ;     д) .

2. Порівняйте значення виразів:

а) і ;    б) і .

3. За яких умов правильною є рівність ?

4. Піднесіть до квадрата:   

а) 5;      б) –3;      в) ;      г) 0,4.

V. Засвоєння нових знань

1. Квадратний корінь із добутку.

Теорема 1. Корінь із добутку двох невід’ємних множників дорівнює добутку коренів із цих множників: якщо а≥ 0   і b≥0, то .

Доведення

1) Вирази , і мають зміст, якщо а≥ 0 , b≥0. ≥0  , оскільки ≥0 і ≥0 .

2) за властивістю степеня.

Отже, вираз набуває невід’ємного значення, і квадрат цього виразу дорівнює ab. Тому рівність правильна і є тотожністю.

Наприклад, .

Доведена теорема поширюється на випадок, коли кількість множників під знаком кореня більша за два.

Наприклад, , якщо , , .

2. Квадратний корінь із дробу.

Теорема 2. Корінь із дробу з невід’ємним чисельником і додатним знаменником дорівнює кореню з чисельника, який поділений на корінь зі знаменника: якщо а≥ 0  і , то .

Доведення

1) Якщо а≥ 0  і , то кожен із виразів і має зміст і ≥ 0.

2) 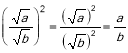за властивістю степеня.

Отже, за означенням арифметичного квадратного кореня, якщо а≥ 0 і , то . Ця рівність є тотожністю, оскільки вона справджується для всіх допустимих значень змінних a і b.

Наприклад, ; .

Помінявши в тотожностях і місцями їхні ліві та праві частини, маємо: і . Цими тотожностями користуються в процесі множення й ділення арифметичних квадратних коренів.

Наприклад, ; .

3. Квадратний корінь зі степеня.

Теорема. Корінь зі степеня , де а≥ 0, n — натуральне число, дорівнює :      

Доведення

1) Оскільки а ≥ 0, то  ≥ 0.

      2) , тому за означенням арифметичного квадратного кореня, якщо а≥ 0,  

          то .

Наприклад, ; .

4. Тотожність .

Доведемо, що за будь-якого значення a виконується рівність .

Доведення

1) За будь-якого значення a вираз має зміст і | а |≥ 0.

2) , оскільки якщо а ≥ 0, то і , а якщо , то

і . Отже, рівність є правильною.

Наприклад, ; .

Розглянемо приклад.

Приклад. Спростіть вираз , якщо , .

Розв’язання

.

VI. Первинне закріплення знань

▪ Виконання усних вправ

Знайдіть значення виразу:

а) ; б) ; в) ; г) ; д) ; е) ; є) ; ж) ;

з) ; і) ; ї) ; к) ; л) ; м) ; н) .

2. Спростіть вираз:

а) , якщо x < 0;

б) , якщо c <  0;

в) , якщо а <  0;

г) , якщо ;

д) , якщо а < 0 і  b< 0 ;

е) , якщо  b< 0

VII. Підбиття підсумків уроку

▪ Завдання класу 

Знайдіть і виправте помилки в записі:

а) ;

б) ;

в) ;

г) ;

д) .

    VIII. Домашнє завдання