Властивості арифметичного квадратного кореня

Урок № 8-А_____________________8-Б_______________

Дата      8-А_____________________8-Б_______________

Властивості арифметичного квадратного кореня

Мета:  Вивчити властивості квадратних коренів, навчитися застосовувати дані властивості в обчисленнях, сприяти розвитку усного мовлення учнів (вміння володіти предметною мовою), сприяти формуванню толерантного ставлення до себе, однокласникам, учителю, підтримувати інтерес до досліджуваного предмета.

Обладнання: приклади на дошці (на А4)

Тип уроку: урок вивчення нової теми

Ход урока

I етап. Організаційний.

II етап. Актуалізація опорних знань.

- Дайте визначення арифметичного квадратного кореня.

-Зараз вам потрібно буде вирішити приклади, які написані на дошці. Ваше завдання мовчки вийти і вибрати собі приклад, відповідь до якого ви знаєте. Після чого, передаєте естафету наступному учневі класу на вибір. Тільки головна умова: НІХТО НЕ ГОВОРИТЬ !!!

А.

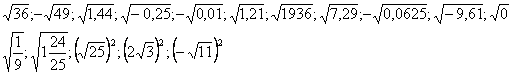
В.

III етап. Вивчення нової теми. Метод проблемного навчання

- Зараз вам потрібно самостійно вирішити два приклади різними способами і з них вибрати оптимальний варіант рішень, обґрунтувати свій вибір. (Один учень біля дошки)

1) Розрахуйте:

Вибір оптимального варіанту

    1 варіант обчислення:

2 варіант обчислення:

- Який спосіб зручніше і швидше?

- Таким чином, ми з вами вивели і довели 1 властивість квадратних коренів, який називається властивість квадратного кореня з добутку

.

В конспект

- Для розуміння, засвоєння і закріплення даного властивості усно виконаємо наступну вправу.

Первинне закріплення. Обчисліть:

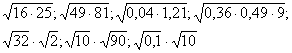
- Зверніть увагу, що ця властивість можна застосовувати як зліва направо, так і справа наліво.

2) Обчисліть

1 варіант обчислення:

2 варіант обчислення:

• Какой способ удобней и быстрее?

- Это второе свойство квадратных корней и называется оно свойство квадратного корня из дроби.

В конспект

- За допомогою даного властивості обчисліть:

Первинне закріплення. Обчисліть

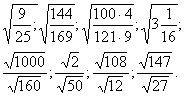
- Також зверніть увагу на те, що дану властивість можна застосовувати як зліва направо, так і справа наліво

- Як винести множник з-під кореня?

- Розкласти подкоренное вираз на множники і витягти коріння, які витягуються. дивимося:

= = 6

- Як бачимо, все вийшло. Це, до речі, не найшвидший, але самий надійний спосіб. Розкладати число на найменші множники, а потім збирати в купки однакові. Спосіб успішно застосовується і при перемножуванні незручних коренів.

- Наприклад, треба обчислити:

**= = =2*3*3*6 = 108

- От і все. Звичайно, розкладати до упору не обов'язково. Все визначається вашими особистими здібностями. Довели приклад до стану, коли вам все ясно, значить, можна так і залишити. Головне - не помилятися. Не людина для математики, а математика для людини!

- Як внести число під корінь, як ви думаєте?

Припустимо, що у нас є ось такий вираз:

 2

- Чи можна заховати двійку всередину кореня?

- Добре! Якщо з двійки зробити корінь, спрацює формула множення коренів. А як з двійки корінь зробити?

- Правильно! Двійка - це корінь квадратний з чотирьох!

Ось і пишемо:

2= *=

- Який висновок можна зробити?

-Будь-яке  невід'ємне число, помножене на корінь, можна внести під корінь. Але - не забувайте! - під коренем це число стане квадратом самого себе. Цю дія - внесення числа під корінь - можна ще назвати множенням числа на корінь.

В конспект

IV етап. Закріплення вивченого матеріалу.

1) Обчисліть

- Чи можна в даному випадку застосувати властивість квадратного кореня з добутку. Перевірити практично.

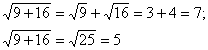
Висновок про те, що властивості квадратних коренів існують тільки для твору і ділення квадратних коренів (піднесення до степеню квадратних коренів), повинні сформулювати учні

Робота з підручником

Самостійна робота

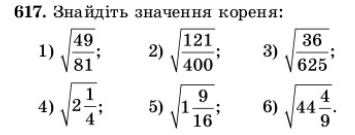
Робота в парах

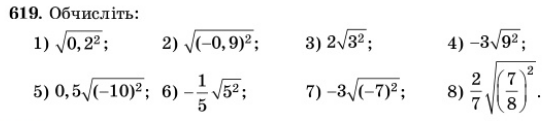
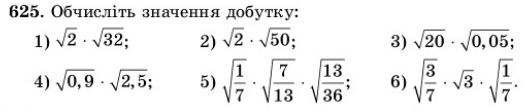
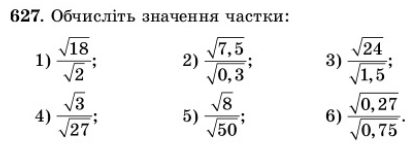
Колективна робота

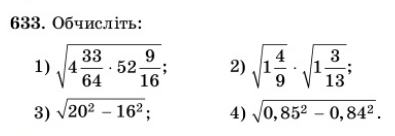
V етап. Домашнє завдання: