Властивості кутів трикутника. Урок 2.

Геометрія 7-клас. УРОК №4.

Тема. Властивості кутів трикутника.

Формування  компетентностей:

Математична компетентність : удосконалити вміння  застосовувати теорему про суму кутів трикутника, а також про висновки з цієї теореми до розв’язування задач; засвоїти поняття зовнішнього кута трикутника та зміст теореми про градусну міру зовнішнього кута трикутника; сформувати вміння знаходити на рисунку і виконувати зображення зовнішнього кута трикутника при даній вершині трикутника; записувати теорему про градусну міру зовнішнього кута трикутника відповідно до умови задачі; використовувати властивість зовнішнього кута трикутника разом з теоремою про суму кутів трикутника для розв'язання задач, передбачених програмою.

 Ключові компетентності: Спілкування державною мовою – уміння розуміти, пояснювати і перетворювати тексти математичних задач (усно і письмово), грамотно висловлюватися рідною мовою;

Інформаційно-цифрова компетентність – уміння доводити істинність тверджень;

Уміння вчитися впродовж життя ­­­– організовувати та планувати свою навчальну діяльність; 

Тип уроку: засвоєння і застосування знань, вироблення вмінь

Обладнання: підручник, набір демонстраційного креслярського приладдя,  комп’ютер,презентація.

Хід уроку

І. Організаційний етап   

ІІ. Перевірка домашнього завдання   

Перевірка  засвоєння знань  і вмінь попереднього уроку .

Математичний  диктант

Варіант 1

1. Закінчіть речення «Сума кутів будь-якого трикутника дорівнює ...».
2. Чи існує трикутник з двома прямими кутами?
3. Чи існує трикутник, два кути якого дорівнюють від­повідно 120° і  80°?
4. Один із кутів трикутника тупий. Які два інших кути?
5. Чому дорівнює кут М трикутника МКО,  якщо кут К має градусну міру  70° , кут О — 30°?
6. У трикутнику ABC кут А у два рази більший за кут С, кут В в три рази більший за кут С. Якого виду трикут­ник ABC?

Варіант 2

1. Чи існує трикутник, два кути якого дорівнюють від­повідно 130° та 70°?
2. Чи існує трикутник з двома тупими кутами?

Закінчіть речення «Сума кутів будь-якого

3. трикутника дорівнює ...».
4. Один із кутів трикутника прямий. Якими є два інші кути?
5. Чому дорівнює кут М трикутника МКО, якщо кут М дорівнює 110°, кут О дорівнює 30°?
6. У трикутнику ABC кут А на 20° менший від кута В, а кут С на 20° більший за кут В. Якого виду трикутник ABC?

Після диктанту обов'язково робимо корекцію — аналізує­мо помилки учнів, спираючись на відповідний навчальний матеріал.

III. Мотивація навчальної діяльності учнів. Формулювання мети і завдань уроку

Практична робота.

1. Накресліть:

а) гострокутний трикутник ABC;

б) прямокутний трикутник ABC;

в) тупокутний трикутник ABC.

2. Проведіть промінь BD, доповняльний до променя ВА. Якими є кути ABC і DBC.
3. Виміряйте кути трикутника ABC і кут DBC. Порівняйте градусні міри кутів: DBC і ABC, DBC і суми А і С в ABC. Що ви помітили?

 Фронтальна бесіда. 

1. Чи завжди можна побудувати кут DBC способом, опи­саним в умові задачі, і скільки таких кутів можна по­будувати при кожній вершині?
2. Чи буде співвідношення між кутом DBC і сумою кутів А і С, отримане при виконанні завдання «експерименталь­ним шляхом» загальною властивістю в будь-якому три­кутнику?
3. Пошук відповідей на поставлені запитання і становить ос­новну дидактичну мету уроку.

IV. Актуалізація опорних знань і вмінь учнів

Усні   вправи

1. Знайдіть градусну міру кута х (рис. 56).

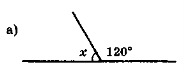
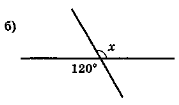
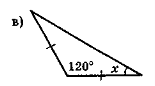
Рис. 56

2. Чи існує трикутник з двома:

а) тупими кутами;

б) прямими кутами?

3. Чи існує трикутник, усі кути якого:

а) гострі, менші від  60°;

б) гострі, більші за  60° ?

V. Засвоєння нових знань

План вивчення нового матеріалу

1. Означення зовнішнього кута трикутника.(підготовлене практичною роботою)
2. Властивість зовнішнього кута трикутника.
3. Наслідок із властивості зовнішнього кута трикутника.

VI. Удосконалення знань і вмінь.

Усні   вправи

1. Для трикутника ABC побудуйте зовнішні кути при вер­шині С.
2. Кут В трикутника ABC дорівнює 140°. Чому дорівнює зовнішній кут при вершині В?
3. Назвіть зовнішні кути:

а) при вершинах D і Е трикутника DKE (рис. 57, а);

б) при вершині Е трикутника KEN (рис. 57, а);

в) при вершинах D і Е трикутника DBE (рис. 57, б);

г) при вершині О трикутника AOD (рис. 57, в).

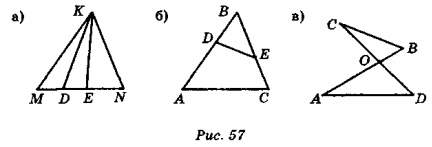
4. Обчисліть кут х (рис. 58) найраціональнішим спосо­бом.

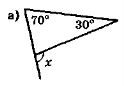
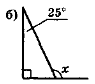
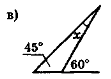
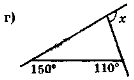
Рис. 58

 Робота з підручником№ 

Додатково:1) зовнішні кути трикутника відносяться як 3 : 4 : 5. Знайти внутрішні кути трикутника.

2) Один із внутрішніх кутів трикутника дорівнює 40°, а один із зовнішніх кутів — 125°. Знайдіть решту внутрішніх та зовнішніх кутів трикутника.

3) Знайдіть внутрішні кути трикутника, якщо сума двох із них дорівнює 150°, а один із зовнішніх кутів дорівнює  80° .

VII. Підсумки уроку

Для кутів трикутника MNK (рис. 59) записати якомога більше правильних рівностей.

VIII. Домашнє завдання

1. § 10 (конспект уроку, с. 81, 82) — вивчити теорію.
2. Письмово: № 298, 306 (б, г).
3. Додаткові задачі.