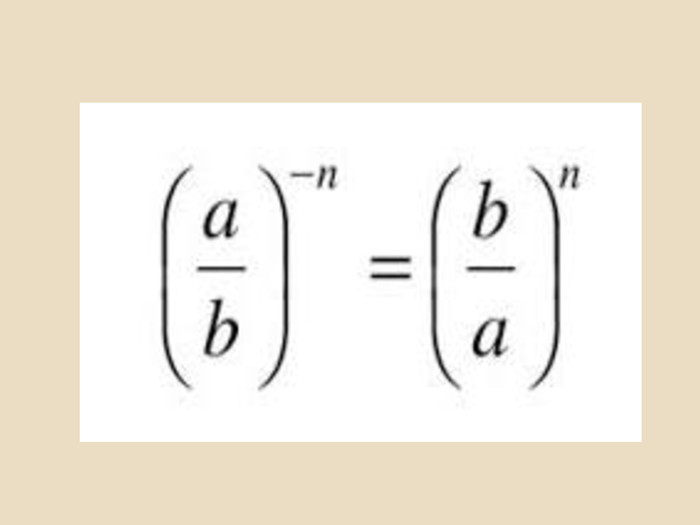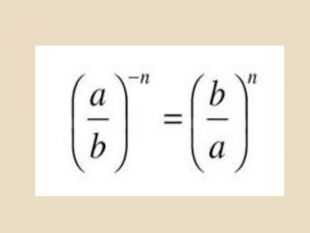Властивості степеня з цілим показником

Тема: Степінь з цілим показником. Мета уроку : Ø Освітня:Познайомити учнів з поняттям степеня з цілим показником і його властивостями. Навчити застосовувати вивчені поняття і властивості при обчисленнях і перетвореннях. Ø Розвивальна:Розвивати уміння застосовувати теоретичні знання на практиці. Розвивати пізнавальну активність, мислення, увагу і пам'ять, уміння слухати товариша, математичну мову. Ø Виховна:Виховувати інтерес до математики через міжпредметні зв'язки з літературою, астрономією, хімією, історією. Виховання цілеспрямованості, здобуття системи цінностей через сприйняття афоризмів і крилатих виразів. Тип уроку :засвоєння знань, умінь і навичок. Обладнання: Презентація, роздатковий матеріал, підручник. Хід уроку I. Організаційний етап. ІI. Актуалізація опорних знань та вмінь Що називається степенем числа? Що означає а^5, в^3, 7^10… Виконання усних вправ 1. Прочитайте вираз, назвавши основу і показник степеня: 1) 54; 2) (6,1)9; 3) 101; 4) (-8)5; 5) 017; 6) -(〖1/7)〗^5. 2. Піднесіть до квадрата: 1) 4; 2) -3; 3) 1/5; 4) 2/3; 5)-3/7 6) 0,9. 3. Піднесіть до куба: 1) 3; 2) -2; 3) 1/3; 4)-2/5; 5)-1/2; 6) -0,1. 4. Визначте знак виразу, не виконуючи піднесення до степеня: 1)〖 (1/4)〗^3; 2) 〖-(1/4)〗^7; 3) 〖(-1/4)〗^2; 4) 〖-(1/4)〗^2; 5) (-2)9 6) -210 7) (-2)10; 8) -29; 5.Укажіть порядок дій в обчисленні значення виразів: 152 – 34; ; (32 – 23)20. III. Формулювання мети і завдань уроку ІV. Засвоєння знань Нагадаємо, що в 7 класі ми вивчали степінь з натуральним показником. За означенням степеня , якщо п > 1, п — натуральне число і а1=а. У математиці, а також під час розв'язування задач прак¬тичного змісту, наприклад з фізики або хімії, трапляються степені, показник яких нуль або ціле від'ємне число. Степінь з від'ємним показником можна знайти в науковій та довідко¬вій літературі. Наприклад, масу атома гелію, записують так: 6,64∙10-27 кг. Як розуміти зміст запису 10-27? Розглянемо степені числа 3 з показниками 1, 2, 3, 4...: У цьому рядку кожне наступне число у 3 рази більше за попереднє. Продовжимо рядок вліво, зменшуючи кожного разу показник степеня на 1. 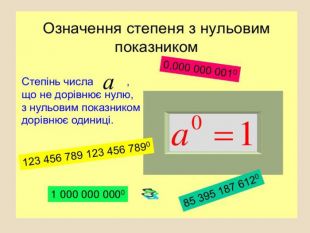Дістанемо: Число 3° повинно бути в 3 рази менше за 31=3. Але в 3 рази меншим за число 3 є число 1, отже, 30 = 1. Така сама рівність а0 = 1 буде виконуватися для будь-якої основи а, відмінної від нуля. 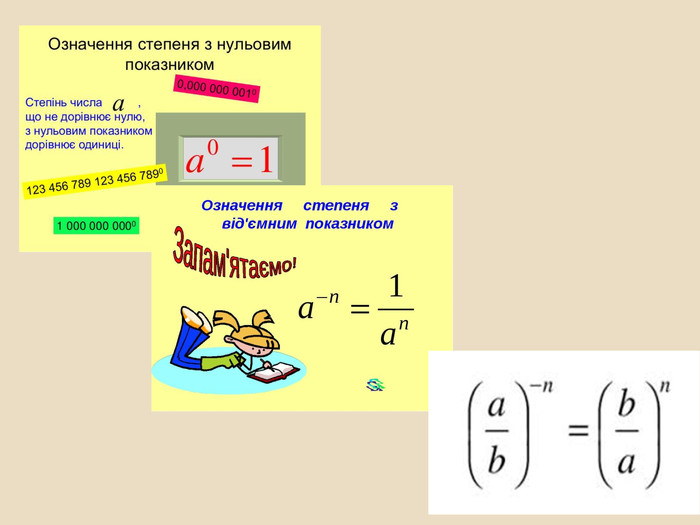Степінь числа а, яке не дорівнює нулю, з нульовим показником дорівнює одиниці: Зліва у рядку від числа 30 = 1 стоїть число 3-1. Це число у 3 рази менше за 1, тобто дорівнює 1/3. Отже, 3^(-1)=1/3=1/3^1 . Міркуючи далі аналогічно, дістанемо і т.д. Доцільно прийняти наступне означення степеня з цілим від'ємним показником (-n): an={█(⏟(aaa…a,)┬(n-раз ) якщо натуральне число n>1;@a, якщо n=1;@1, якщо n=0 і a≠0;@1/a^(-n) , якщо n-ціле від'ємне і a≠0.)┤ Приклад 1. Замінити степінь з цілим від’ємним показником дробом: Розв’язання: Приклад 2. Замінити дріб степенем з цілим від’ємним показником: Розв’язання: Приклад 3. Виконати піднесення до степеня: Розв’язання: Розглянемо піднесення до від’ємного цілого степеня дробу a/b. Якщо n - натуральне число і a≠0, маємо: Отже, Приклад 4. Обчислити: Розв’язання: Відповідь: Означення степеня з цілим від’ємним показником 1.Якщо: a≠0, n — натуральне число, то 〖 a〗^(-n)=1/a^n Приклад. 1) 3^(-2)=1/3^2 =1/9; 2. Якщо: a ≠0, n=0; то a 0=1 Приклади.1) (-2,6)0=1; 2) 〖(2/3)〗^0=1 3. Записи 0 0, 0 -п не мають змісту 4. Якщо: a/b≠0; n — натуральне число, то 〖(a/b)〗^(-n)=〖(b/a)〗^n. Приклад. 〖(2/3)〗^(-2)=〖(2/3)〗^2=9/4=2 1/4 5.Обчисліть значення виразу: 〖(3/8)〗^(-1)+9-2-(-2,6)0= Крок1. Замінити степені з від'ємними показниками на степені з натуральними показниками: =8/3 + 1/9^2 - (-2,6)0 = Крок 2. Виконати піднесення до степеня: =8/3 + 1/81 - 1= Крок 3. Виконати дії з дробами: 22/3 – 1 + 1/81 = 155/81 V. Формування вмінь Виконання усних вправ Обчисліть: 24; (-3)2; (0,1)3; (-1)8; ; ; (-15)9; 0,30; ; 00. Замініть дробом степінь із цілим від'ємним показником. Заповніть пропуски. ; ; ; . Замініть дріб степенем із цілим від'ємним показником: ; ; ; Вчитель: Діти, вам необхідно було самостійно попрацювати з додатковою літературою, відшукати історичні відомості про степінь з цілим від’ємним показником . Метод «Мікрофон» Учень 1. Від’ємні показники степеня першим систематично почав вживати І. Ньютон, хоч вони були відомі раніше. У 1667 році він зазначив «як алгебраїсти замість аа, ааа і т.д. пишуть а2, а3, і т.д. так я замість 1/a^2 , 1/a^3 пишу, а-2, а -3 » Учень 2. До нашого часу збереглися глиняні плитки з таблицями квадратів і кубів натуральних чисел, зроблені стародавніми вавилонянами. Згодом учені стали розглядати четвертий, п’ятий та вищі степені, називаючи їх спочатку квадрато – квадратом, кубо – квадратом і т.д. Учень 3. Степінь з нульовим показником запровадили в V столітті незалежно один від одного самаркандець Аль – Каші і француз Н. Шюке. Учень 4. Француз Н. Шюке також використовував степені з від’ємними показниками. Учень 5. Теорію степенів з від’ємними показниками розробив у XVІІ столітті англійський математик Джорж Валліс. Виконання письмових вправ №263, 264 , 266 усно №268, 270, 272 письмово самостійно (робота в парах) VI. Підсумки уроку Тестові завдання 1. Тотожно рівним виразу 7-3 є вираз: а) -73; б) 1/7^3 ; в) 1/(7∙3) г) 1/7^(-3) . 2. Тотожно рівним дробу 1/8 є вираз: а) 23 ; б) 24; в) 4-2; г) 2-3 3. Значення виразу 2-3 + 2-2 дорівнює: а) -10; б) 3/8; в) 5/12; г) 12. 4. Тотожним до степеня (3/4)-2 є вираз: а) (4/3)-2 ; б) (4/3)∙2 ; в)(4/3)2 г) (3 )/4 ∙(-2) VII. Домашнє завдання Опрацювати § 9 №265, 267, 269, 271.