Урок-подорож країною “Тригонометрія” в 10 класі. “Властивості та графіки тригонометричних функцій”

Структура уроку-подорожі

Тема: “Властивості та графіки тригонометричних функцій”

Мета: засвоїти властивості тригонометричних функцій, навчитися будувати графіки; формувати вміння застосовувати знання на практиці; розвивати пізнавальну активність; виховувати наполегливість, старанність, вміння працювати в колективі.

Хід проведення

1. Організаційний момент 1 хв
2. Повідомлення теми і мети 2 хв

 

3. Актуалізація опорних знань

 Перша зупинка “Теоретична” 10-15 хв

(показ відео, відповіді на запитання, “Лайфхак “Тригонометрія на пальцях”)

 

4. Пояснення нового матеріалу

Друга зупинка “Дослідницька” 20 хв

(будуємо графіки синуса і косинуса,

формулюємо властивості, заповнюємо таблицю,

оглядово знайомимося із графіками тангенса і котангенса)

Виступ  студентів “Тригонометрія в природі і біології” 3-5 хв

_________________________________________________________

5.               Застосування знань і вмінь

Третя зупинка “Творча лабораторія”

(будуємо графік функції за допомогою геометричних перетворень, перевіряємо за допомогою програмного засобу) 15 хв

Виступ студентів “Тригонометрія в фізиці” (демонстрація експерименту) 5-7 хв

 

6. Формування вмінь та навичок

Четверта зупинка “Пригодницька” 10 хв

(розв’язуємо вправи усно, біля дошки, у форматі ЗНО)

Виступ студента “Тригонометрія в архітектурі” 3 хв

 

7. Підсумки Вірш-побажання 2 хв
8. Рефлексія Зупинка “Сувенірне містечко”
9. Оцінювання 1 хв
10. Домашнє завдання 1 хв

 

Тема: Графіки та властивості тригонометричних функцій

Мета:

Познайомити з тригонометричними функціями y=sin x, y=cos x, y = tg x, y = ctg x; сформувати вміння будувати графіки функцій; домогтися засвоєння властивостей тригонометричних функцій; створити умови для формування вмінь та навичок студентів самостійно поглиблювати знання, застосовувати їх у практичній діяльності.

Розвивати пізнавальну активність студентів; логічне та аналітичне мислення, інтерес до вивчення теми.

Виховувати увагу, старанність, культуру математичної мови та запису, впевненість у своїх силах.

Тип уроку: Засвоєння знань, умінь та навичок

Форма проведення: урок-екскурсія

Місце проведення: навчальна аудиторія

Обладнання: глобус, кепки, проектор, туристичний маршрут (карта), тригонометричне коло, таблиця “Геометричні перетворення графіків функцій”.

Література: Бевз Г. П. Математика: Алгебра і початки аналізу та геометрія. Рівень стандарту: підруч. для 10 кл. загальної середньої освіти/Г. П. Бевз, В. Г. Бевз. – К.: Видавничий дім “Освіта”, 2018. – 288 с. : іл.

Хід уроку

1. Організаційний момент

Доброго дня! Рада вітати усіх на занятті з математики. Сподіваюся, усі присутні  студенти та гості проведуть свій час із користю у нашому товаристві.

 Зараз куди не подивися, усі люблять подорожувати! (звертаю увагу на глобус). А куди б нам помандрувати? Може в Китай? Але китайської ми не знаємо. Можна було б в США. Але англійську теж не дуже добре знаємо, хоча… ми ж знаємо універсальну мову – мову математики! Навіть якщо ми не знаємо англійської, ми з легкістю зуміємо розібратися із завданням з математики, бо в усіх країнах вона однакова!

І сьогодні ми станемо учасниками цікавої подорожі в країну під назвою “Тригонометрія”. Туристами будете ви, а екскурсоводом я. На допомогу нашому товариству прийдуть – карта, що слугує маршрутом екскурсії!

Бачимо у вас на партах кепки, – головний атрибут туристів! Звичайно, вони для того, щоб ніякі перешкоди і погода за вікном не зіпсували нам сонячного настрою, який, сподіваюся, буде панувати на за під час подорожі.

 

2. Повідомлення теми і мети

Отож, давайте знайомитися. Мене звати Пасічник Ольга Валентинівна. Ось уже восьмий рік я працюю екскурсоводом по математиці. І сьогодні запрошую вас в надзвичайну країну “Тригонометрія”.

Давайте розпочинати.

Тригонометрія! Як багато говорять про цю країну. Але, що ми про неї знаємо? Яка ж історія її виникнення? Які вона має кордони? Як зображають її на картах? Якими історичними пам’ятками володіє? І головне – це те, де саме ми можемо її зустріти у повсякденному житті? Думаю, на усі ці питання ми дамо відповідь в ході нашої з вами екскурсії.

Перед нами карта подорожі.

Сьогодні ми пройдемся новим туристичним маршрутом, де на вас чекають зупинки із дослідження, майстер-клас, творча лабораторія, пригоди, а в кінці, як завжди, – багато фотоматеріалів з подорожі та сувенірне містечко.

А ще ми побуваємо ми в місті, де дізнаємося які головні артерії країни –  графіки тригонометричних функцій, відвідаємо майстер-клас, на якому навчимося їх будувати і сформулюємо властивості, а також використаємо набуті знання під час проходження інтелектуальних вправ.

Знаю, що серед учасників екскурсії є присутні біологи, фізики, архітектори. Думаю, що кожен з вас зможе подивитися на цю країну з своєї точки зору.  І думки кожного ми вислухаємо в ході екскурсії.

Перша наша зупинка “ТЕОРЕТИЧНА”

3. Актуалізація опорних знань (Старт) 

 

Пропоную переглянути короткий відеосюжет.

(показ відео про Індію)

Отже, цим коротеньким відео ми доторкнулися до історії створення тригонометрії і побачили, що вона сягає більше двох тисячоліть. Усе, як ми бачили, почалося з астрономії. Розділ математики, що лежить на перетині алгебри та геометрії і вивчає співвідношення між сторонами й кутами трикутників, дозволяючи проводити кутові обчислення через спеціально визначені функції кутів.

Тепер же тригонометрія має широкий спектр застосування в різних науках. І в цьому ми сьогодні переконаємось.

Говорять хто володіє інформацією, той володіє світом. Тож кожен, хто вирушає у подорож старається озброїтись головними характеристиками країни. А що відомо вам про неї та її пам’ятки?

Давайте дізнаємося як ви орієнтуєтесь в теоретичному просторі теми?

 

Вправа “Скринька пам’яті”

1. Що таке одиничне коло?
2. Що таке радіанна міра кута?
3. Що таке кут повороту?
4.  Що називають одиничним колом?
5. Що таке кут повороту?
6. Назвіть в радіанах кути: 90°, 180°, 270°, 360°.
7. Виразіть в градусах кути:
8.  Визначте в якій чверті закінчується кут:  110°, 290°, - 30°, -235°?
9.  Що називається синусом числа α? Косинусом числа α?
10. Де розміщені числові значення  sin α, cos α?
11.  Що називається тангенсом, котангенсом числа α?
12.  Які знаки мають тригонометричні функції в кожній з координатних чвертей?
13. Знайдіть значення виразу:

2 sin30°+cos30°, 3tg – 2sin.

14. Визначте знак виразу: 

sin67°cos265°tg376°;

sin(-268°)cos18°sin 2.

15. Чому sinα, cosα, tgα, ctgα є тригонометричними функціями числового аргументу?
16. За якою схемою описують властивості функцій?

• Область визначення?
• Множина значень?
• Яка функція називається парною (непарною) Що відомо про їх графіки?

• Яка функція називається періодичною?
• Нулі функції?
• Який основний період функцій y = sin x, y = cos x , y = tg x, y = ctg x.

 

Дуже часто потрібно знати напам’ять значення тригонометричних функцій основних кутів. Може комусь із вас відомо цікавий метод, як з легкістю запам’ятати значення головних кутів?

Виступ червоної кепки

(Лайфхак “Тригонометрію на пальцях”)

Висновки … Бачу серед вас дуже допитливих туристів! Молодці! Гарно впоралися із завданням. Найактивнішими туристами можна назвати…..

Пора рухатися далі.

І  наша Друга зупинка “Дослідницька”.

 

4. Пояснення нового матеріалу.

Ну що ж, ви довели, що можете вирушати у подорож, багато головних характеристик країни Тригонометрія ми вже знаємо.

На цій зупинці ми дізнаємося чим приваблива наша Тригонометрія, як зображають її на картах. Ми побудуємо графіки тригонометричних функцій.

Отже, до вашої уваги майстер-клас із побудови графіків тригонометричних функцій. Я виконую на дошці, а ви повторюєте за мною, будуєте  їх у ваші туристичні довідники – зошити.

Пояснення і побудова графіків на дошці.

За графіком зручно досліджувати властивості тригонометричних функцій. Тому побудуємо графік функції .

Для цього будемо використовувати знаннями властивостей, які ми знаємо.

Відкладемо від початку координат на осі абсцис відрізок  довжиною , взявши за одиницю довжини радіус одиничного кола. Поділимо цей відрізок на 6 рівних частин.

Оскільки функція періодична, то побудуємо графік на проміжку , а решту утворимо шляхом паралельного перенесення вздовж осі ох вліво і вправо на 2π.

Скористаємося даними таблиці значень тригонометричних функцій деяких кутів. Знайдемо кілька опорних точок:

x	0		π		2π
y	0	1	0	-1	0

Утворена крива називається синусоїдою. Від лат. вигин, кривизна.

Графік функції  y = сos х легко побудувати, скориставшись формулою зведення:= соs х, паралельним перенесенням графіка функції вздовж осі Ох на одиниць вліво.

Графік функції y = сos х називають косинусоїдою.

Перед нами таблиця з властивостями. Давайте її заповнимо y = sin x, а для  y = cos x самостійно:

Властивості	y = sin x	y = cos x
Область визначення D(y)	xR
Область значень E(y)
Парність	Непарна    sin (–x) = – sin x
Періодичність	Періодична,    T = 2π
Нулі функції	sin x = 0, при
Проміжки знакосталості
Проміжки зростання і спадання	Зростає ,n
	Спадає ,n
Найбільше і найменше значення	у=1, при х =
	у= –1, при х =

 

! Оглядово знайомимось із графіком тангенса і котангенса.

Висновки

Отже з цієї зупинки ми дізналися, що головними артеріями країни Тригонометрія є графіки, що мають свої назви, – синусоїда, косинусоїда.

Надзвичайно багато природних явищ описуються за допомогою цих функцій! Думаю, що приклади можете навести ви, учасники туристичної групи. Пора нам дізнатися таємницю кожної кепки, що є на партах. Давайте послухаємо точку зору туристів-біологів та медиків стосовно пройденого маршруту. Думаю, що інформація, яку ви щойно прослухали стосується в деякій мірі вас.

Виступ студентів “Тригонометрія в природі та біології”

Висновки…дійсно зв'язок природи з тригонометрією вражаючий!

Ми з легкістю пройшли майстер-клас і тепер переходимо но наступної зупинки “Творча лабораторія”.

Третя зупинка “Творча лабораторія”

5. Застосування знань, умінь і навичок

Ще 2000 років тому китайський педагог Конфуцій сказав те, що я чую -  я забуваю. Те, що я чую і бачу, - я трохи пам’ятаю. Те, що я чую, бачу обговорюю і роблю – я починаю розуміти. Тож закликаю вас до співпраці! Ми наблизилися до різних пригод та розваг, що трапляються в подорожах.

На цій зупинці побачимо як видозмінюються графіки тригонометричних функції за допомогою геометричних перетворень. А які геометричні перетворення ми знаємо?

Вчитель звертає увагу на таблицю “Геометричні перетворення графіків функцій”

Робота з дошкою:

у =  – sin (x + )

1. Побудуємо графік функції y = sin x
2.  Будуємо графік  y = - sin x
3. Побудуємо у = –sin (x + )

Давайте з метою економії часу за допомогою математичного пакету GeoGebra розглянемо інші перетворення.

Студент-асистент вводить дані в  програму.

А) y = 3cos x (розтягнути від ох в 3 рази)

Б) y = cos 2x, (стиснути до Оу вдвічі)  

В) у = cos (x + ) (перенести вліво на 2 одиниці)

Г) y = cos x–2

Д)

Бачимо різні варіації графіків в залежності від формули задання функції.

Знаю, що учасники екскурсії з блакитними кепками занурилися в Тригонометрію з точки зору фізики. Отже, прошу висловити свою думку туристів-фізиків.

Виступ студентів “Тригонометрія в фізиці”

(Розповідь про коливальні рухи у фізиці.

 Демонстрація експерименту)

Висновки… як бачимо, тригонометрія має широкий спектр застосування у фізиці.

А ще безмежний простір для розвитку інтелекту.

 

6. Узагальнення і систематизація знань.

Четверта зупинка “Пригодницька”

Ми потихеньку наблизилися до останньої зупинки “Пригодницька”. Тут на вас чекають різні пригоди та розваги, що трапляються в подорожах.

Вам потрібно буде проявити усі свої знання і здібності, взяти участь в різних розвагах, які пропонує наша Тригонометрія.

 Після проходження завдань ми потрапимо в сувенірне містечко, де кожен обере собі сувенір на згадку про нашу подорож.

1. Знайти область визначення функції:

;

2. Парною чи непарною є функція?

; ;

3. Визначте найменший додатний період функції:

y = sin 5x; y = cos 1,5 x;

4. Яке з чисел 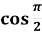, cos 2, cos 5, cos 6π, cos 1– є найбільшим?

Завдання ЗНО:

1. Установити відповідність між функціями (1-4) та їх парністю (А-Д)

                               В) Непарна   

                                 Г) Ні парна, ні непарна

                                                                   Д)Парна і непарна

 

2. Установити відповідність між функціями (1-4) та їх найменшими додатними періодами (А-Д).

 

Висновок. Усі гарно попрацювали. Залишилася ще точка зору архітектора. 

Давайте послухаємо.

Виступ помаранчевої кепки

 (Розповідь про творіння архітектури)

Висновки. Ми можемо доповнити фотозвіт екскурсії вашими цікавими матеріалами.

 

7. Підсумки

Давайте підсумуємо нашу подорож. Під час екскурсії ми дізналися про періодичні функції, навчилися будувати їх графіки, побачили застосування тригонометрії в різних сферах діяльності людини, заповнили фотоальбом подорожі! Сподіваюся наша екскурсія була пізнавальною та цікавою! І хочу завершити її словами:

Життя таке: то плюс, то мінус,

Не знаю вам як, а мені

На функцію це схоже «синус»,

На графік лиш поглянь її.

Вершина, спад і знов підйоми –

Закономірності прості.

І майже все, як нам відомо,

Періодично у житті.

Я б вам хотіла побажати

Свій графік по життю знайти

Але дозволити пораду?

По тангенсу йдіть до мети.

Як ви гадаєте, чому я вам порадила йти до мети саме по тангенсу?

(Тому що графік цієї функції зростає на всій області визначення)

 

8. Рефлексія “Сувенірне містечко”

Пропоную обрати для себе смайлик-сувенір, що відповідає вашому настрою на згадку про нашу подорож.

 

9. Домашнє завдання

Домашнім завданням буде опрацювати туристичний довідник по тригонометрії – ваш конспект. Заповнити властивості функцціїї Побудувати графік