Внесок вивчення математики у формування інформаційно-цифрової компетентності учнів

Внесок вивчення математики у формування інформаційно-цифрової компетентності учнів

Анотація

У роботі розглянуто приклади форми і змісту роботи на уроці математики, спрямовані на формування інформаційно-цифрової компетентності учнів, не з точки зору використання ІКТ у процесі викладання, а з точки зору підготовки мисленнєвих процесів і способів дій.

Розвиток науки і техніки, засобів комунікації привів до вибухового зростання маси знань, необхідних для успішної професійної, соціальної та особистісної самореалізації людини, та до їх швидкого оновлення. Тому перед сучасною освітою постає завдання не скільки допомогти учню засвоїти певну інформацію, скільки озброїти його вміннями і рисами, необхідними для пошуку і отримання знань і, що найголовніше, їх вдалого застосування. Цю задачу освіта України вирішує шляхом реалізації компетентністного підходу до навчання.

Законом України «Про освіту» компетентність визначена як «динамічна комбінація знань, умінь, навичок, способів мислення, поглядів, цінностей, інших особистих якостей, що визначає здатність особи успішно соціалізуватися, провадити професійну та/або подальшу навчальну діяльність» [3]. Більше того, викладацька діяльність визначається як «діяльність, спрямована на формування знань, інших компетентностей..» [3].

Сьогодні важко уявити сферу діяльності людини, у якій не були б задіяні інформаційно-комунікаційні технології. То ж однією із ключових освітніх компетентностей визначено інформаційно-комунікаційну компетентність.

На фоні динамічних змін у суспільстві, науці, технологіях, математика здається символом консервативності. Проте оновлення змісту предмета не обмежується застосуванням задач прикладного чи професійного спрямування. Математика має потужний потенціал не лише у формуванні ключових компетентностей, а й у розвитку мислення учня, підготовки його до діяльності в епоху цифрових технологій.

Навчальна програма з математики у пояснювальній записці вичерпно визначає внесок вивчення математики у формування ключових компетентностей. Зокрема, у процесі вивчення математики формуються такі компоненти інформаційно-цифрової компетентності:

-уміння: структурувати дані; діяти за алгоритмом та складати алгоритми; визначати достатність даних для розв’язання задачі; використовувати різні знакові системи; знаходити інформацію та оцінювати її достовірність; доводити істинність тверджень [5].

Розглянемо окремі приклади форми і змісту роботи на уроці математики з точки зору формування ключових компетентностей.

Уміння структурувати дані.

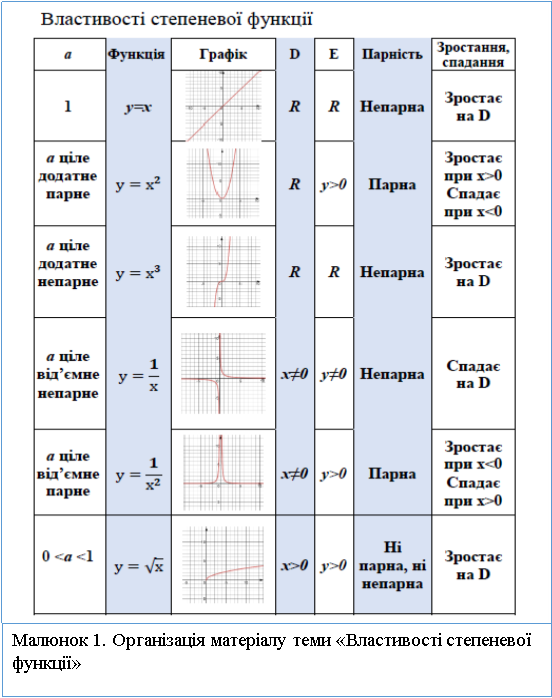Для структурування матеріалу уроку використовуються таблиці різного змісту і призначення. Один із видів – концептуальні таблиці. Складання таких таблиць доцільно застосовувати при порівнянні кількох властивостей об’єктів. По вертикалі розташовуємо список об’єктів, по горизонталі – перелік властивостей, що підлягають порівнянню. Наприклад, при вивченні теми «Степеневі функції, їх властивості і графіки» учні мають засвоїти знання про цілий перелік властивостей степеневих функцій відповідно до показника степеня. Матеріал такого уроку систематизуємо у таблицю (мал. 1), у верхньому рядку якої перелічено властивості функції, у першому стовпчику поміщено список функцій. Ця таблиця може бути заповнена в ході вивчення нового матеріалу колективно, в якості домашньої роботи, на етапі закріплення та систематизації знань, з метою перевірки засвоєння знань.

Використання у ході вивчення нового матеріалу методу аналогій також може бути підкріплено складанням таблиці. Найпростіший приклад – вивчення теми «Координати і вектори у просторі». У першому стовпчику таблиці викладач пропонує записати основні факти теми. Другий стовпчик учні можуть заповнити самостійно (за умови достатньої підготовленості групи), використовуючи знання зі шкільного курсу геометрії про координати і вектори на площині. Третій стовпчик, який містить матеріал теми, що вивчається, учні можуть заповнювати самостійно чи в ході евристичної бесіди з допомогою викладача.

До цього ж розділу можна віднести складання схем класифікації об’єктів. Прикладом може слугувати класифікація геометричних тіл. Використання такої схеми у ході уроку забезпечує логічність вивчення матеріалу, систематизацію знань та можливість швидкого пошуку і повторення властивостей тіл.

Уміння діяти за алгоритмом та складати алгоритми.

Алгоритм - це послідовність точно визначених дій, що однозначно приводять до вирішення поставленого завдання. Переважна більшість математичних задач, що відповідають репродуктивному рівню засвоєння знань, передбачають розв’язування за алгоритмом.

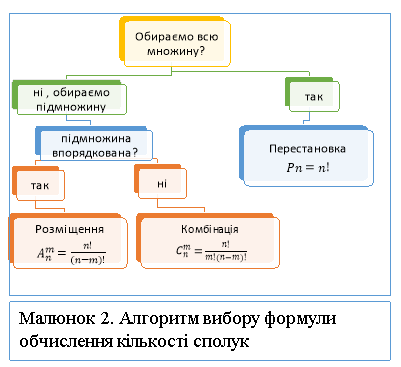На початковому етапі розв’язування нового типу задач алгоритм дій візуалізуємо за допомогою плакатів, схем, опорних конспектів. З метою поглиблення запам’ятовування і усвідомлення порядку дій застосовуємо гру «Ланцюжок»: окремі учні чи команди по черзі виконують кроки алгоритму для розв’язування певної задачі. Така форма роботи сприяє не лише засвоєнню матеріалу, а й дозволяє утримати увагу учнів, внести змагальницький компонент до уроку як додатковий засіб активізації пізнавальної діяльності учнів. Наприклад, алгоритм вибору формули для обчислення кількості сполук (мал.2), тема «Елементи комбінаторики, теорії ймовірності та математичної статистики»

Іншим видом діяльності є створення алгоритму. Таке завдання можна ставити перед учнями за умови достатнього розуміння ними навчального матеріалу. Формально, складання плану розв’язування задачі на основі аналізу її умови також є алгоритмом. Після розв’язування кількох однотипних задач використовуємо складання алгоритму з метою узагальнення знань і вмінь. Наприклад, розв’язування задачі на знаходження первісної, що задовольняє певні умови, може мати евристичний характер, а у підсумку учні формулюють алгоритм для розв’язування цілого типу задач: знайти загальний вигляд первісної; підставити координати точки; розв’язати рівняння відносно С; записати відповідь.

За умови достатнього рівня знань учнів групи, можливе складання алгоритму для розв’язування певного типу задач на основі раніше засвоєної інформації, без попереднього виконання вправ. У цьому випадку можливе застосування технології «Мозковий штурм». Приклад: алгоритм дослідження функції за допомогою похідної. При складанні такого алгоритму учні використовують раніше набуті знання з тем «Функції, їхні властивості і графіки» та «Похідна та її застосування». В ході роботи треба визначити логічну послідовність кроків, врахувати можливості і переваги дослідження функції за допомогою похідної, визначити спосіб виконання окремих кроків.

Уміння визначати достатність даних для розв’язання задачі.

До вказаного пункту звертаємося щоразу при розв’язуванні геометричної задачі на обчислення, що передбачає два і більше логічних кроки. При аналізі умови задачі визначаємо формулу для обчислення шуканої величини і встановлюємо, чи маємо всі дані для її використання. Наступним кроком є складання плану пошуку даних, яких не вистачає: додаткові побудови, обчислення величин із використанням даних елементів фігури, виведення величини із додаткових формул.

Уміння використовувати різні знакові системи

Природною, і звичною для кожної людини, знаковою системою є мова. Математика має свою «мову», яка є штучною знаковою системою, тісно переплітається з мовою, але має власні особливості. Ця знакова система є апріорною, логічною, загальноприйнятою, значно формалізованою.

В ході уроку окремо приділяється увага умінню читати математичні вирази та записувати твердження за допомогою математичних символів (таке уміння відповідає обов’язковому рівню знань). Слід відмітити важливість таких вимог. Якщо учень читає про себе число «1,2» як «одна друга», що є типовою помилкою, то при записі дробу «одна ціла дві десятих» у режимі диктування, найімовірніше, запише «1/2».

Перехід між знаковими системами в межах предмета здійснюється при переході від градусної до радіанної міри кута, при перетворенні дробів (звичайних і десяткових, що використовується і у межах матеріалу математики старшої школи) тощо. 

Уміння знаходити інформацію та оцінювати її достовірність

Дуже суперечливим є питання використання учнями телефону на уроці. З одного боку це привід для списування, з іншого – потужне джерело додаткової інформації. Урок математики є чудовою нагодою показати учням, що будь-яка інформація потребує ретельного відбору.

Часто в ході уроку виникає потреба пригадати математичні факти, вивчені у середній школі і вже призабуті. У такому випадку використовуємо інтернет. Але неточне формулювання запиту та використання першої сторінки результатів пошуку приводить до зачитування складних формулювань із Вікіпедії. Тому формулюємо головне правило використання інтернет-підказок: «Кожне слово у знайденій відповіді має бути відомим і зрозумілим». Слідування цьому правилу формує потребу у критичному аналізі інформації та може ініціювати цілий ланцюг запитів і грунтовне повторення матеріалу.

Доводити істинність тверджень

Способи формування даного компоненту очевидні: згідно логічної структури предмета, кожне нове твердження доводиться на основі аксіом чи вже доведених раніше тверджень. У процесі доведення теорем чи задач учні формують навички пошуку і відбору інформації також, навчаються враховувати вихідні положення та обирати способи дій, сприймають основи формальної логіки.

Висновок

На уроці математики сформованість інформаційно-комунікаційної компетентності учнів відкриває можливості застосування комп’ютерних технологій, використання електронних джерел інформації. Але і вивчення математики у формування компетентності здійснює значний внесок саме у галузі формування світогляду та способів мислення учня.

Використані джерела

1.               https://mon.gov.ua/ua/osvita/zagalna-serednya-osvita/navchalni-programi/navchalni-programi-dlya-10-11-klasiv - Навчальна програма з математики (алгебра і початки аналізу та геометрія) для учнів 10-11 класів загальноосвітніх навчальних закладів. Рівень стандарту, затверджена Наказом Міністерства освіти і науки № 1407 від 23 жовтня 2017 року
2.               Бібік Н. М. Переваги і ризики запровадження компетентнісного підходу в шкільній освіті / Н. М. Бібік // Український педагогічний журнал. - 2015. - № 1. - С. 47-58.
3.               Дмитренко К.А. Звичайні форми роботи – новий підхід: розвиваємо ключові компетентності: метод. посіб. / К.А. Дмитренко, М.В. 221 Коновалова, О.П. Семиволос, С.В. Бекетова. – Х.: ВГ «Основа», 2018. – 119 [1] с.:табл, схеми, рис. – (серія «Нові формати освіти»)
4.               Компетентнісно орієнтована методика навчання математики в основній школі: Метод. посібник  / О.І.Глобін, М.І. Бурда, Д.В. Васильєва, В.В. Волошена, О.П. Вашуленко, Н.Д. Мацько, Т.М. Хмара. — К.: Педагогічна думка,  2015. – 245с.
5.               Про освіту : Закон України від 05.09.2017 р. № 2145-VIII. Відомості Верховної Ради. 2017. 27 верес. (№ 38-39-380). C. 380