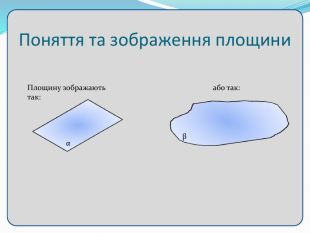
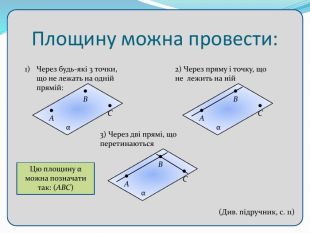
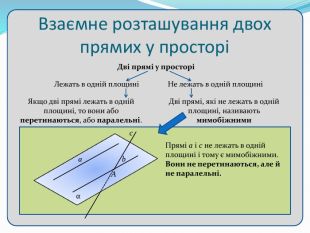
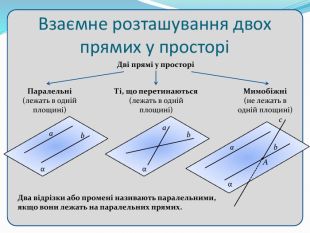
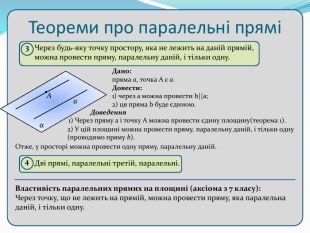
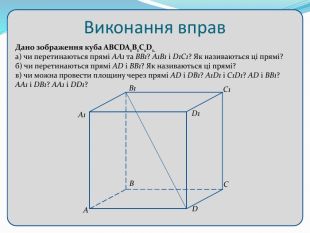
Взаємне розташування прямих у просторі
Про матеріал
презентація до уроку 10 клас, математика
МІстить матеріал для посторення основних понять стереометрії;
Схеми та малюнки щодо розташування прямих у просторі Перегляд файлу
Зміст слайдів


Безкоштовний сертифікат
про публікацію авторської розробки
про публікацію авторської розробки
Щоб отримати, додайте розробку
Додати розробку