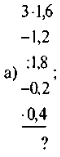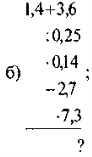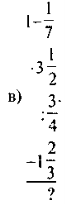Ймовірність випадкової події. Графічне порівняння шансів

Тема.  Ймовірність випадкової події. Графічне порівняння шансів

Мета: сформувати уявлення учнів про ймовірність випадкової події, як про кількісну оцінку можливості появи тієї чи іншої акції, шансу її появи; опанувати спосіб визначення ймовірності випадкових подій, що спирається на ці уявлення.

Тип уроку: застосування знань, умінь, навичок

Хід уроку

I. Перевірка домашнього завдання

Учні заповнюють і здають бланки відповідей завдань домашньої роботи:

№ 2. а) ні; б) так. № 3. г) № 4. в)

Після цього вчитель називає правильні відповіді і з учнями обгово­рює можливі запитання, також приклади достовірних, неможливих та випадкових подій, що їх придумали учні (з. 1).

II. Актуалізація опорних знань

Усні вправи

1. Які з наведених подій є випадковими; достовірними; неможливими:

а) У Харкові 23 липня 2010 року піде сніг;

б) взимку падає сніг;

в) з торбинки, в якій дві сині і дві жовті кульки, витягуємо зелену кульку;

г) після осені настає зима?

2. У скриньці 5 білих і 10 чорних куль. З неї вийняли 5 куль. Чи правда, що серед них:

а) обов'язково є біла куля;

б) обов'язково є чорна куля;

в) може бути біла куля;

г) не може бути чорної кулі?

4. Порівняйте: а) 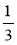; 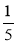і .
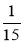5. Зобразіть на координатному промені числа: 0; 1; 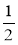; ; 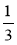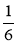. Яке з останніх
   трьох найближче до 1?

III. Засвоєння нових знань

 Оскільки ми не даємо учням строгого означення ймовірності, а вертаємось до їхньої інтуїції, то даємо це поняття як кількісну можливість (шанс) появи події на конкретних зрозумілих прикла­дах, супроводжуючи їх рисунками.

Задача 1. У скриньці дві білі, дві чорні і дві червоні кульки. Витя­гуємо навмання п'ять з них.

1) Чи будуть серед них білі?

Відповідь. Так — зобразимо на координатному промені точкою з ко­ординатою 1 (див. рис).

2) Чи можуть серед них бути три білі?

Відповідь. Ні, в жодному разі — зображаємо числом 0.

3) Чи можуть серед них бути дві білі?

Відповідь. Можливо, так, а може, й ні — позначаємо числом 0 і 1 (ближче до 0 чи до 1 — ми не знаємо).

Отже, будемо вважати, що:

а) достовірним подіям відповідає число 1;

б) неможливим подіям відповідає число 0;

в) випадковим подіям відповідає число р, що задовольняє умову 0 < р < 1.

Задача 2. Є три торбинки з кулями: у першій — 3 кулі; другій — 5 куль; третій — 15 куль. У кожній з них по одній червоній кулі. Потрібно вийняти червону кулю. З якої торбини доцільно вийняти кулю, щоб шанси вийняти червону кулю були найбільшими?

Розв'язання. Зрозуміло, що тут усі події є випадковими, але шанси різні й у першому випадку — він один з 3-х; у другому один з 5-ти; у третьому — один з 15-ти. Тому зобразимо на координатному промені ; і . (див. рис).

Бачимо, що найменші шанси — точка, найближча до 0 — вийняти червону кульку з третього мішечка, а найбільші — точка, найближча до 1 — вийняти червону кульку із першого мішечка.

Отже, можливість відбутися тій чи іншій випадковій події може ха­рактеризуватися числом р, що 0 < р < 1, і чим більше р, тим ймовірність події більша.

Порівнювати шанси (ймовірність) можна, порівнюючи відповідні числа.

IV. Засвоєння вмінь

1. Є три мішечки, що містять відповідно 500, 100 , 1 000 ґудзиків. У кожному мішечку по одному синьому ґудзику. З якого мішечка доцільно
   вийняти ґудзик (не підглядаючи), щоб було більше шансів вийняти
   синій? Ваші уявлення про шанси вийняти синій ґудзик із трьох
   мішечків зобразіть графічно. На координатному промені поставте під
   точками номер відповідного мішечка.
2. Є три мішечки зі 100 ґудзиками в кожному. В цих мішечках 10,1,5 ґуд­зиків відповідно. Треба, не заглядаючи в мішечок, вийняти один
   синій ґудзик. З якого мішечка треба виймати ґудзики, щоб мож­ливість дістати синій ґудзик була найбільшою? Ваші уявлення зобразіть графічно у вигляді точок на координатному промені, про­ставивши під точками номер мішечка.
3. У скриньці білих куль у 5 разів більше, ніж чорних. Із скриньки нав­мання виймається одна куля. Кулю якого кольору більше можливості дістати— білого чи чорного?
4. * У коробці 15 кульок: білих, червоних і чорних. Білих кульок у 7 разів більше, ніж червоних. Навмання з коробки виймаємо одну кульку. Порівняйте шанси появи білої, чорної та червоної кульки. Зобразіть відповідь графічно.

V. Підсумки уроку

Тестові запитання

Перед вами три скриньки: у першій — 10 монет, у другій — 50 монет, у третій — 100 монет. У якій зі скриньок найлегше знайти золоту монету?

а) У першій; б) у другій; в) у третій; г) однаково важко в кожній скриньці.

VI. Домашнє завдання

Задача 1. Три скриньки місять по 100 монет. У першій — одна золота монета, у другій — дві золоті монети, у третій — п'ять. У якій зі скриньок найлегше знайти золоту монету?

Проілюструйте свої міркування рисунком.

Задача 2. У коробці лежать 17 цукерок: шоколадні, карамелі та іриски. Шоколадних у 8 разів менше, ніж ірисок. Навмання виймаємо одну цукерку. Яку цукерку більше шансів дістати: карамельку чи іриску?

Задача 3. Підкинули два гральних кубики (гральні кістки). Яка сума балів має більше шансів з'явитися: 2 чи 5?

Завдання на повторення.

Порівняйте значення виразів:

а) 22,592 : 32 – 0,248  і  1,25 · 541 – 675,802;

б) (162 – 38) · 2,5 – 68,8 : 16   і   58 · 5,3 – 110,4.