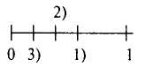Ймовірність випадкової події. Обчислення ймовірності

Тема.  Ймовірність випадкової події. Обчислення ймовірності

Мета: спираючись на сформовані уявлення про зміст поняття «ви­падкова подія» та про порівняння шансів випадкових подій, сформувати уявлення про ймовірність випадкової події як про число, яке показує, в якій з випадкових подій більше шансів для настання; спираючись на означення, навчити учнів обчислювати ймовірність випадкових подій за класичним означенням у найпростіших задачах.

Тип уроку: засвоєння нових знань.

Хід уроку

І. Перевірка домашнього завдання

Задача 1. Можливі варіанти: ГГ, ГН, НГ, НН.

Одарка запропонувала несправедливий варіант.

Задача 2. Кількість можливих варіантів — 36.

II. Актуалізація опорних знань

Усні вправи

1. Які з названих подій є достовірними? неможливими? випадковими?

а) Вода (замерзає) перетворюється на кригу при 0°С;

б) після літа настає зима;

в) цього року на Харківщині одержать гарний врожай пшениці.

Наведіть свої приклади неможливих, достовірних, випадкових подій.

2. Перед вами три скриньки з ґудзиками: в першій — 20 ґудзиків, у другій — 30, у третій — 40 ґудзиків, серед яких один — червоний. Із якої скриньки найлегше все вийняти, не дивлячись, червоний ґудзик?

а) першої; б) другої; в) третьої; г) однаково складно з будь-якої.

3. Вам запропонували придбати електронний годинник за 1 грн з додатковою умовою: ви сплачуєте 1 грн, а потім підкидаєте тричі гральний кубик. Якщо всі три рази випаде 6 балів, то годинник ваш, в іншому випадку годинник залишається продавцю. На вашу думку, якими сло­вами можна охарактеризувати подію «Годинник дістанеться вам»?

а) Практично вірогідно; б) практично неможливо;

в) рівноможливо з подією «Годинник залишається вам»;

г) утруднюся з відповіддю.

4. Запишіть у відсотках числа: 0,52; 0,05; 2; 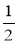; ; 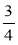; 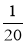1.

III. Засвоєння знань

1. Мотивація навчальної діяльності

 Проводимо бесіду, в якій попри того, що ми зробили під час розв'язування усних вправ, ще раз повторюємо основні поняття, які було розглянуто на попередніх уроках теми. Але наприкінці підводимо до підсумку, що досі ми тільки говорили про види подій та порівнювали шанси настання кількох подій. Виникає за­питання:

А чи можна «виміряти» шанс настання події і якщо можна, то як?

2. Формування знань

 Шестикласники ще не готові для сприйняття строгого означення класичної ймовірності (яке дається в 11 класі), але на інтуїтив­ному рівні поняття про ймовірність як числову характеристику частоти настання тієї чи іншої події вони сприймають. Тому план бесіди, яку проводимо далі може бути таким:

1.   Ймовірність як числова характеристика частоти появи подій або число, що є відношенням кількості наслідків, що ведуть до настання даної події, до кількості всіх можливих наслідків.
2.   Ймовірність достовірної та неможливої подій.
3.   Приклади задач на обчислення імовірностей подій.

Бесіда

1) Під імовірністю випадкової події ми розуміємо число, яке харак­теризує частоту появи даної події.

Наприклад

Якщо за умови 100 підкидань монети герб випав 52 рази, то ймовірність випадання герба дорівнює = 0,52 = 52%.

Якщо ж ми не в змозі провести багато однакових експериментів, щоб таким чином знайти ймовірність події, можна ймовірність обчис­лювати за такою схемою:

а) Знайдемо кількість усіх можливих варіантів, які мають однакові
шанси для появи (або перебираємо всі варіанти, або обчисленням).

б) Знайдемо кількість варіантів, які ведуть до появи даної події.

в) Знайдемо ймовірність р за формулою: р = .

2) Наприклад

Задача 1. Яка ймовірність того, що навмання вирваний з нового ка­лендаря аркуш відповідає 30-му числу, якщо в році 365 днів?

Розв'язання. Оскільки в році 365 днів, у календарі 365 аркушів, вири­ваємо один навмання, то рівні шанси є вирвати будь-який з цих 365 аркушів; тому я = 365. У році 12 місяців, але тільки в 11 є 30-е число (виняток — лютий), тому аркушів, що задовольняють умову всього 11, отже, т = 11. Маємо: р ==.

IV. Засвоєння вмінь

Усні вправи

1. В ящику лежить 10 кульок, три з яких білі. Яка ймовірність того, що вибрана навмання одна кулька — біла?
2. З букв розрізної абетки складене слово «три». Потім букви перемішу­ють і навмання беруть одну за одною. Знайдіть ймовірність, що буде складене початкове слово.
3. З ящика, в якому 4 білих, 3 чорних і 7 червоних кульок, вийміть одну
   кульку. Яка ймовірність того, що вона: а) біла; б) чорна; в) червона?

Письмові вправи

Задача 1. Усі літери української абетки написані на 32 однакових картках. Яка ймовірність того, що написана на картці літера буде на по­значення голосного, якщо картка витягується навмання?

Задача 2. Яка ймовірність того, що навмання вибране натуральне число від одного до 30 включно є дільником числа 30?

Задача 3. З 25 екзаменаційних білетів, що пронумеровані числами від 1 до 25, навмання обирають один. Яка ймовірність того, що номер витягнутого білета є число, що кратне трьом?

Задача 4. Двоє повинні поділити між собою 5 однакових горіхів. Один з них ховає горіхи у дві коробки будь-яким можливим способом, а інший обирає будь-яку коробку. Яка ймовірність того, що той, хто відгадує, дістане 3 горіхи. Що більш ймовірно: дістане він горіхи чи ні?

V. Підсумки уроку
Бліцтест

В ящику лежать 10 кульок: 3 чорні, а інші білі. Яка ймовірність того, що з ящика навмання виймуть:

а) одну білу; б) одну чорну; в)* дві білих кульки.

VI. Домашнє завдання

Повторити: означення достовірних, неможливих та випадкових подій; порівняння шансів подій графічним способом та за допомогою варіантів.

Задача 1. На тарілці лежать 8 однакових на вигляд пиріжків: три — з м'ясом, решта — з повидлом. Який пиріжок більш ймовірно взяти, якщо брати пиріжки навмання: з повидлом чи з м'ясом?

Задача 2. На 5 окремих картках написані літери слова «шторм». Картки перемішують і навмання беруть одну за одною. Яка ймовірність того, що ми складемо дане слово?

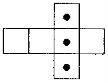
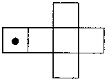Задача 3. Одночасно кидають дві гральні кістки, розгортки яких зображені на рис.

Якщо зверху з'явиться грань з намальованим кружечком, то це означає, що випав один бал; якщо ж на верхній грані нічого не зображено — нуль балів. Порівняйте шанси появи суми 0, 1, 2 бали (сума балів береться на обох кістках). Зобразіть шанси графічно.