Прийоми та методи самостійної роботи

на уроках математики

Зміст

1. Вступ
2. Організація та види самостійної роботи
3. Прийоми та методи самостійної роботи на уроках математики
4. Розробки уроків з елементами самостійної роботи
5. Висновки
6. Список використаних джерел

1. Вступ

Серед методів, які спрямовані на активізацію пізнавальної діяльності учнів, важлива роль належить самостійній роботі.

Термін  самостійна   робота   вживають у різних значеннях. Часто так називають окремі уроки, присвячені самостійному розв'язуванню задач, які дуже схожі на контрольні роботи. Але це тільки один з видів самостій­ної роботи, причому не основний.

У термін «самостійна робота» ми вкладаємо значно ширший зміст, відноситимемо сюди і самостійне вивчення теорії за підруч­ником, і самостійне доведення теорем, і самостійне розв'язування задач, виконання різних завдань: тестів, математичних диктантів, лабораторних робіт, практикумів, семінарів, розгадування вікторин, участь в КВК, математичних олімпіадах, конкурсах, турнірах, круглих столах, дискусіях, проектах, МАН, ЗНО і ДПА. Самостійну роботу учнів слід розглядати як метод навчання, як освітню технологію.

Навчатись можна не тільки з слів учителя, не тільки під час ко­лективного розв'язування задач і вправ, а й самостійно. В умовах звичайної загальноосвітньої школи корисно час від часу пропонувати учням різні види самостійної роботи.

Працюючи самостійно, учні, як правило, глибше вдумуються в зміст опрацьованого матеріалу, краще зосереджують свою увагу, ніж це звичайно буває при поясненнях учителя або розповідях учнів. Тому знання, уміння і навички, набуті учнями в ре­зультаті добре організованої самостійної роботи, бувають  міцнішими і ґрунтовнішими. Крім   того, у процесі самостійної роботи в   учнів виховується  наполегливість,   увага,  витримка та  інші корисні якості.

2. Організація та види самостійної роботи

Серед методів, які спрямовані на активізацію пізнавальної діяльності учнів, важлива роль належить самостійній роботі.

Термін  самостійна   робота   вживають у різних значеннях. Часто так називають окремі уроки, присвячені самостійному розв'язуванню задач, які дуже схожі на контрольні роботи. Але це тільки один з видів самостій­ної роботи, причому не основний.

У термін «самостійна робота» ми вкладаємо значно ширший зміст, відноситимемо сюди і самостійне вивчення теорії за підруч­ником, і самостійне доведення теорем, і самостійне розв'язування задач, виконання різних завдань: тестів, математичних диктантів, лабораторних робіт, практикумів, семінарів, розгадування вікторин, участь в КВК, математичних олімпіадах, конкурсах, турнірах, круглих столах, дискусіях, проектах, МАН, ЗНО і ДПА. Самостійну роботу учнів слід розглядати як метод навчання, як освітню технологію.

Навчатись можна не тільки з слів учителя, не тільки під час ко­лективного розв'язування задач і вправ, а й самостійно. В умовах звичайної загальноосвітньої школи корисно час від часу пропонувати учням різні види самостійної роботи.

Працюючи самостійно, учні, як правило, глибше вдумуються в зміст опрацьованого матеріалу, краще зосереджують свою увагу, ніж це звичайно буває при поясненнях учителя або розповідях учнів. Тому знання, уміння і навички, набуті учнями в ре­зультаті добре організованої самостійної роботи, бувають  міцнішими і ґрунтовнішими. Крім   того, у процесі самостійної роботи в   учнів виховується  наполегливість,   увага,  витримка та  інші корисні якості.

Самостійне вивчення теорії за підручником

Одним з видів самостійної роботи  учнів з математики в класі є самостійне вивчення теорії за підручником.

Пропонувати учням самостійно опрацьовувати за підручником теоретичний матеріал треба хоча б три-чотири рази за семестр (залеж­но від того, як вони вміють працювати з книгою). Основна мета таких завдань — навчити учнів читати математичний текст, інакше кажучи, навчити їх учитися.

Які особливості математичного тексту? Чим відрізняється він, наприклад, від тексту художніх, історичних книг?

По-перше, наявністю багатьох математичних понять, термінів, формул, символів. Коли учень не знає хоч якого-небудь терміна чи символу, що є в тексті, він не зможе його зрозуміти.

По-друге, наявністю різних схематичних рисунків, тісно пов'язаних з текстом. На них треба дивитися паралельно з читанням тексту; читати доводиться не абзацами і навіть не реченнями, а частинами речень.

 По-третє, наявністю багатьох   шрифтів:   курсив,   розрядка,   петит,   якими виділяють означення, теореми, правила,   примітки. 

По-четверте, стилем викладу, чіткістю, лаконічністю, строгістю. Читання мате­матичної  книги потребує максимальної уваги,   міцного   знання всього попереднього матеріалу. У математичному тексті на кожно­му кроці доводиться зустрічатися з різними посиланнями на на­ведені раніше теореми, означення, задачі, аксіоми. Читати мате­матичну книгу треба з олівцем у руках. Уміння  читати математичний   текст   виробляється поступово. Щоб навчити учнів працювати над математичним підручником, треба відвести кілька спеціальних уроків у V і VІ класах (а якщо  потрібно, то й у старших). Можна запропонувати учням такі правила роботи над матема­тичною книгою:

1. Математична книга — не роман; читай її з олівцем у руках.
2. Читаючи, не поспішай, намагайся зрозуміти кожну фразу і кожен абзац.
3. Особливу увагу зверни на означення і теореми, зрозумій роль кожного слова в їх формулюваннях.
4. Читаючи доведення теореми, з'ясуй, що дано і що треба до­вести. Спочатку спробуй довести її самостійно.
5. Якщо читаєш про властивості геометричних фігур, уяви їх, намалюй, використай предмети, що тебе оточують.
6. Ти закінчив читати параграф. Не поспішай братись за іншу роботу. Продумай, про що йшлося в цьому параграфі, найважли­віше намагайся запам'ятати.

Самостійну роботу обов'язково треба перевіряти. Бажано зауважити учням, що відповідати можна не завжди у такій самій послідовності, як у підручнику. Коли учень змінює послідовність, змінює приклади,— це навіть   краще,   ніж   він   розповідатиме точно   за підручником.

У  процесі самостійної роботи учнів з підручником часто відбувається процес злиття навчання з вивченням.

Завдання вчителя полягає в такій організації самостійної роботи учнів, при якій на основі засвоєної з підручників інформації  учні могли б на практиці застосовувати набуті знання, тобто дати свої формулювання означень, теорем, запропонувати інші способи доведення теорем і розв’язування задач. З цією метою доцільно майже на кожному уроці практикувати виконання самостійних завдань тренувального характеру, враховуючи рівень знань кожного учня.

Самостійне розв’язування задач

Самостійне розв'язування задач у школі можна організовувати по-різному. У деяких випадках на   це   корисно   відводити   цілі   уроки,   особливо в старших класах при розв'язуванні громіздких задач і перед конт­рольними  роботами,  щоб  з'ясувати,   чи  можуть  учні  впоратися  з наміченими для контрольної роботи завданнями. їх можна оцінювати (всі або деякі). Під час такої самостійної роботи бажано бути серед учнів, допомагати деяким, робити зауваження для всіх. Цим і відрізняється така самостійна робота від контрольної.

Проте для самостійних робіт зручніше відводити тільки частини уроків — 15—20 хв. Учитель на  уроці  може  пояснити  матеріал, дати  завдання, розв'язати  кілька прикладів колективно,  а потім запропонувати кілька вправ до кінця уроку розв'язати самостійно. Такі роботи можна оцінювати.

Відшукання учнем своїх доведень і способів розв’язання

Добре,  коли  учень  уміє самостійно читати  математичну   книгу,   розв'язувати   задачі   відомих  типів. Але ще краще, коли він намагається знаходити свої доведення,  свої  способи   розв’язування задач, пропонує свої формулювання означень, тео­рем і т. д. Завдання вчителя — заохочувати і підтримувати такі прагнення. Це один з видів самостійної роботи; можна навіть ска­зати, що це найвища форма самостійної роботи учнів. Спостережен­ня показують, що такі учні, які намагаються давати свої доведен­ня і розв'язання задач, є в кожному класі, і тільки від учителя залежить, як культивується в класі така форма самостійної роботи.

Позакласне читання з математики

Великим резервом розширення математичних знань учнів, навичок роботи з книгою і, що не менш важливо, вироблення навичок самоосвіти, може стати бібліотека науково – популярної літератури з математики і її позакласне читання.

При організації позакласного читання вчитель повинен звернути особливу увагу на те, що математична книга, навіть науково - популярна, надзвичайно вимоглива. Робота з нею – це справжня праця розуму, розвиток уявлення, фантазії, пам’яті. Учням доцільно пропонувати і підготувати проект, доповідь, анотацію статті, ознайомитись з новим методом розв’язування задачі .

3. Прийоми та методи самостійної роботи на уроках математики

Урок-лабораторна робота

Лабораторні роботи дають, можливість учням більш повно і свідомо з'ясувати математичні залежності між величинами, знаходити певні закономірності, удосконалити навички вимірювань і обчислень, ро­боти з таблицями, графіками, діаграмами тощо.

Основним етапам лабораторних робіт є: Самостійне виконання учнями (кожним, парами, по варіантах, групами) роботи. Можна провести лабораторні роботи при вивченні тем: „Пряма призма”, „Піраміда”, „Довжина кола”, „Геометричні побудови”,  „Наближені обчислення”.

Урок – практикум

Так називають уроки розв'язування задач із однією чи кількох логічно пов'язаних тем. Основний час на практикумах відводиться на кероване самостійне розв'язування задач. Керівництво роботою може здійснюва­тись як вчителем, так і за допомогою дидактичних матеріалів.

Урок-залік

Найчастіше використовують семінари, на яких узагальнюють та систематизують знання, уміння й навички учнів з великої теми чи кількох тем. План підготовки до семінару вчителю слід  повідомити  на початку вивчен­ня теми.

У планах підготовки більшості семінарів доцільно передбачити такі завдання: знати (означення, теореми, алгоритми); вміти (доводити теореми, розв'язувати конкретні задачі); підготувати реферати; виготови­ти таблиці, моделі; підібрати і розв 'язати задачі практичного характе­ру тощо.

Семінарське заняття з математики має передбачати обов'язкову самоосвітню діяльність кожного учня і колективне обговорення й оцінку її результатів.

Урок-гра

До уроку-заліку учні готуються протягом вивчення всієї теми. На по­чатку вивчення теми вчитель може помістити на стенді "Вивчаємо тему" список запитань, типових вправ обов'язкового рівня, що відповідають початковому та середньому рівням навчальних досягнень учнів, та задач підвищеної складності, що відповідають достатньому та високому рівням засвоєння матеріалу.

Математичний диктант

Математичний диктант – одна з ефективних форм організації самостійної роботи учнів. Це короткочасні письмові контрольні роботи, під час яких учні, сприймаючи завдання на слух (повністю чи частково), виконують його письмово або записують лише результат.

Математичні диктанти бувають навчаючі і контролюючі.

Систематичне використання математичних диктантів дає надійну інформацію про рівень засвоєння нового матеріалу підвищує математичну культуру учнів сприяє розвитку їх мови.

Тести для самостійної роботи та контролю знань

Тести призначаються для організації самостійної роботи учнів, спрямованої на повторення курсу математики і підготовку до навчання у відповідних класах. Тести можуть використовуватися для моніторингового дослідження рівня математичної підготовки учнів, а також для вивчення їхнього математичного розвитку. Проведення вимірювань наприкінці і на початку навчального року є ефективним засобом контролю за динамікою стану математичної підготовки колективу в цілому і кожного учня зокрема. Ефективна організація самостійної роботи учня – одна з головних умов досягнення учнем успіхів у навчанні.

Тести  використовуються під час ЗНО, ДПА.

Специфікою тестової форми перевірки якості знань є досить великий обсяг завдань, що потрібно ви­конати за обмежений проміжок часу самостійно учневі.

Контрольні роботи

Контрольні роботи проводяться для виявлення рівня знань учнів в письмовій формі, яку учні самостійно виконують цілий урок, або 15-20 хв. приблизно два рази на місяць, у старших класах – раз на місяць.

На контрольних роботах учням пропонують розв’язувати задачі або приклади і включають теоретичні питання, доведення теорем, виведення формул тощо. Контрольні роботи дають  у кількох варіантах, або кожному індивідуальну контрольну роботу. Крім обов’язкової частини, можна включати у контрольну роботу і необов’язкову, щоб учень, який виконав завдання не залишився без роботи.

Форми проведення позакласної самостійної роботи

Проектна технологія

Проектна робота - вид роботи (переважно в групах), метою якої є підготовка кінцевого продукту. Мета цього виду роботи - дати учню можливість виконати незалежну(самостійну роботу) роботу, побудовану на знанні матеріалу та уміннях і навичках, здобутих упродовж певного періоду вивчення теми. Проектні роботи ідеальні для різнорівневих груп, оскільки кожне завдання може бути виконане учнями, що мають різний рівень підготовки. У процесі проектної діяльності учні реально спілкуються між собою і з навколишнім світом.

Метод проекту – це метод пошуку, тобто така організація навчання, при якій учні набувають знань в процесі планування та виконання практичних завдань – проектів. Проект дає можливість тісно поєднати теорію з практикою.

Метод проектів дозволяє вчителю надати пріоритет різним видам самостійної діяльності учнів.

Участь школярів в МАН

Підготовка науково-дослідницьких робіт учнів — членів та кандидатів у члени МАН України має на меті якісне оновлення змісту позашкільної освіти учнів, створення системи пошуку і підтримки об­дарованої молоді для формування наукової еліти.

Написання і подальший захист науково - дослідницьких робіт спрямовані на     реалізацію внутрішніх потреб дітей і підлітків у професій­ному самовизначенні, задоволення їхніх запитів у розкритті здібнос­тей та інтересів.

Математичні олімпіади

Метою популяризації математичних ідей та підтримки талановитих школярів, розвиток їх інтелектуальних здібностей є проведення математичних олімпіад, конкурсів „Кенгуру”,  турнірів (ТЮМів), на яких проявляються творчі здібності школярів і які вимагають від учня самостійного розв’язання різних завдань, тестів, і т.д. Для учнів олімпіада є способом перевірки і утвердження свого покликання і одним з видів самостійної роботи.

Домашня робота

Домашня робота - це  теж самостійна робота учня. У домашній (самостійній) роботі учень має навчитись виконувати всі операції, які він спочатку виконував під керівництвом учителя, а тепер має повторити їх стосовно себе (ставити мету, планувати, контролювати, оцінювати).

Вико­нання домашніх завдань сприяє закріпленню і поглибленню поданого на уроці нового матеріалу, допомагає виробити  навички, дисци­плінує  учнів,  привчає їх працювати систематично і самостійно, функція домашньої роботи – навчити дітей вчитися.

   Окремим учням можна давати індивідуальні   домашні завдання; сильнішим доцільно запропонувати кілька важчих за­дач, а слабкішим — легші вправи. Іноді домашні роботи можуть бути і достроковими і виконуватися на заліковий урок. Учитель повинен стежити і за тим, чи справді самостійно   виконують учні домашні завдання.

Дидактичні вимоги до системи самостійних робіт

Під системою самостійних робіт розуміють сукупність взаємопов’язаних і взаємообумовлених видів робіт, які логічно випливають одна з одної та підкоряються загальним завданням освітнього процесу.

Кожна система повинна відповідати визначеним вимогам або принципам. Під час побудови системи самостійних робіт необхідно також дотримуватись певних дидактичних вимог.

1. Система самостійних робіт має сприяти розв’язанню основних дидактичних задач – набуттю учнями глибоких і міцних знань, розвитку в них пізнавальних здібностей, формуванню вмінь самостійно набувати знання, використанню їх на практиці.

2. Система має відповідати основним принципам дидактики, і перш за все принципам доступності та систематичності, зв’язку теорії з практикою, свідомості й творчої активності, принципу навчання на високому науковому рівні.

3. Роботи, які належать до системи, мають бути різноманітними за метою навчання та змістом, щоб забезпечувати формування в учнів запланованого переліку навчальних умінь і навичок.

4. Послідовність виконання домашніх і класних самостійних робіт повинна бути такою, щоби виконання одних видів робіт було логічно пов’язане з іншими, а також готувало учнів до виконання наступних. Успіх розв’язання цієї задачі залежить не тільки від педагогічної майстерності вчителя, а й від того, як він розуміє значення й місце кожної окремої роботи в системі робіт, у розвитку пізнавальних здібностей учнів, їх мислення.

Розробка системи самостійних робіт є необхідною умовою для систематичної, цілеспрямованої організації самостійної діяльності на уроках. Але наявність лише одного системного підходу не визначає успіху роботи вчителя з формування в учнів знань, умінь і навичок. Для цього ще треба знати основні принципи, керуючись якими, можна забезпечити ефективність самостійних робіт, а також методику керівництва їх різними видами.

Принципи керівництва  і особливості самостійної  роботи

Принципи до керівництва самостійною роботою має певні особливості.

1. Самостійна робота повинна мати цілеспрямований характер. Це досягається чітким формулюванням мети роботи. Завдання вчителя полягає в тому, щоб знайти таку форму завдання, яка викликала б у школярів інтерес до роботи та бажання виконувати її якомога краще. Учні повинні усвідомлювати, у чому полягає їх завдання та яким чином буде перевірятись його виконання. Недооцінка вимог веде до того, що учні, не розуміючи мети роботи, роблять не те, що потрібно, і змушені в ході її виконання багато разів звертатись до вчителя
2. Самостійна робота повинна бути справді самостійною та змушувати учня при її виконанні працювати з напруженням. Але не треба перебільшувати зміст і обсяг самостійної роботи, що пропонується учню на кожному етапі навчання. Вона має бути посильною, а самі учні – підготовленими до виконання самостійної роботи теоретично та практично.
3. Спочатку треба сформувати найпростіші навички самостійної роботи. У цьому випадку вчитель має демонструвати на прикладах прийоми виконання самостійної роботи, супроводжувати їх чіткими поясненнями та записами на дошці.
4. Самостійна робота, яка виконується учнями після демонстрації прийомів учителем, носить характер наслідування. Вона не розвиває самостійності в цілому, але має важливе значення для формування найбільш важливих навичок і вмінь, більш високої форми самостійності, при якій учні здатні розробляти та застосовувати свої методи розв’язування задач навчального чи виробничого характеру.
5. Для самостійної роботи треба пропонувати такі завдання, виконання яких не буде шаблонним, вимагатиме застосування знань у новій ситуації. Тільки в цьому випадку самостійна робота сприятиме формуванню ініціативи та пізнавальних здібностей учнів. 
6. При організації самостійної роботи необхідно враховувати й те, що для набуття навчальних компетентностей різним учням потрібен різний проміжок часу. Зробити це можна шляхом диференційованого підходу. Спостерігаючи за роботою класу в цілому та окремих учнів, учитель повинен залучати тих, які добре та швидко впоралися з завданням, до виконання більш важких.
7. Завдання, які пропонують учням для самостійної роботи, повинні зацікавлювати їх. Це досягається завдяки новизні матеріалу, незвичній формі, змісту через розкриття практичного значення запропонованої задачі або методу, яким треба оволодіти.
8. Самостійні роботи учнів необхідно планувати та систематично проводити.
9. При організації самостійної роботи необхідно поєднувати викладання матеріалу вчителем із самостійною роботою учнів. Але треба бути дуже обережним, бо захоплення самостійною роботою може загальмувати швидкість вивчення програмного матеріалу.
10.                    При виконанні самостійних робіт різного виду управління діяльністю учнів має належати вчителю.

Труднощі при проведенні самостійної роботи

Учні закінчують роботу не одночасно. Для цього потрібно дати додаткові завдання, для тих  учнів, що працюють швидше. Тяжко підібрати завдання, однаково посильні всім учням.  Ще важче підібрати геометричні завдання, однаково посильні для всіх. Трудно організувати перевірку самостійної роботи. Інколи вчитель збирає зошити всіх учнів. Це добра форма перевірки, але її не завжди можна зробити. Тому слід використовувати інші методи перевірки самостійної роботи.  Наприклад, спочатку виконують самостійну роботу, а в кінці її виконання один з учнів записує розв’язок задачі на дошці для перевірки. Це приводить до лишньої трати часу. Значно краще, коли один-два учні виконують самостійну роботу на відкидних дошках. 

В залежності від тієї педагогічної мети, яка переслідується при проведенні самостійних робіт, вони можуть бути розділені на дві основні групи: роботи навчальні й перевірочні роботи.

Навчальні роботи поділяються на:

•    роботи, спрямовані на підготовкн дітей до сприйняття нового навчального матеріалу;
•    роботи, спрямовані на отримання нових знань;
•    роботи, спрямовані на розширення й поглиблення набутих знань;
•    роботи тренувального характеру, метою яких є закріплення набутих раніше знань, умінь і навичок.

Перевірочні роботи поділяються на: класні (математичний диктант, тести, контрольні роботи) і домашні.

4. Розробки уроків з елементами самостійної роботи

Тема уроку:  Перерізи конуса площинами. Зрізаний конус.

Мета уроку:  розглянути основні види перерізів конуса – переріз,

перпендикулярний до осі; переріз, що проходить через дві твірні; формування поняття зрізаного конуса.

Обладнання:  моделі конусів, зрізаних конусів, слайди презентацій.

І. Перевірка домашнього завдання

1. Перевірити наявність домашнього завдання та відповісти на запитання, які виникли в учнів при виконанні домашнього завдання.
2. Презентації учнів на теми «Циліндр», «Конус».

ІІ. Сприйняття й усвідомлення нового матеріалу

Перерізи конуса площинами (слайд №1, 2)

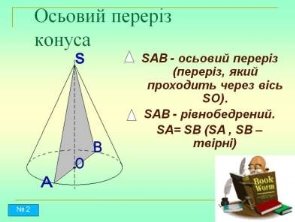
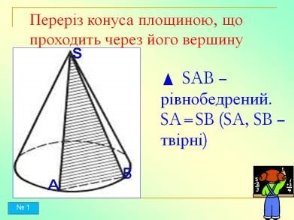
Проведемо в конусі переріз площиною, яка проходить через дві твірні  SA і SB, площина перетне основу конуса по хорді AB, отже, переріз конуса площиною, яка проходить через вершину, - трикутник.

Розв’язування  задач

1. Твірна конуса L. Знайти площу перерізу, проведеного через дві твірні, кут між якими дорівнює a.(Відповідь.)
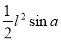2. Твірна конуса L, а радіус основи r. Знайти площу перерізу, проведеного через вершину конуса і хорду основи, що стягує дугу, кутова величина якого дорівнює a. (Відповідь. )
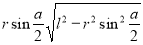3. Висота конуса дорівнює H. Знайдіть площу перерізу, що проходить через вершину конуса і хорду основи, яка стягує дугу, кутова величина якої a, якщо площина перерізу утворює з площиною основи кут 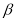. (Відповідь. )
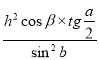4. Задача. Радіус основи конуса R, а твірна нахилена до площини основи під кутом a. Через вершину конуса проведено площину під кутом φ до його висоти. Знайдіть площу утвореного перерізу.

5.Задача. Висота конуса 20,радіус його основи 25. Знайдіть площу перерізу, проведеного через вершину, якщо відстань від нього до центра основи конуса дорівнює 12.

Слайд № 3

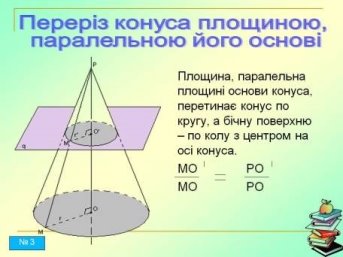
Теорема. Площина, паралельна площині основи конуса, перетинає конус по кругу, а бічну поверхню – по колу з центром на осі конуса

Д о в е д е н н я: Розглянемо перетворення гомотетії з центром у вершині конуса S, яке суміщає січну площину (слайд № 3) з площиною основи. При цьому переріз конуса суміститься з основою конуса. Отже, переріз конуса площиною є круг, а переріз бічної поверхні – коло з центром на осі конуса.

Розв’язування  задач

Задача. Конус перетнуто площиною, паралельною основі, на відстані d від вершини. Знайдіть площу перерізу, якщо радіус основи конуса R, а висота H.

Зрізаний конус  (Слайд № 4, 5)

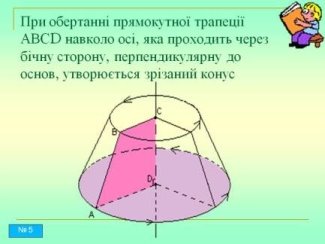
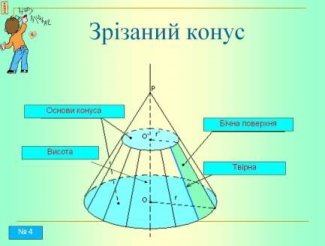
Площина, яка паралельна основі конуса і перетинає конус, відтинає від нього менший конус. Частина, що залишилася, називається зрізаним конусом.

Зрізаним конусом  називається частина конуса, що лежить між основою і площиною, паралельною основі

Розв’язування  задач

Задача.  Радіуси основ зрізаног конуса R і  r, твірна нахилена до основи під кутом 45⁰. Знайдіть висоту.

Задача . Радіуси основ зрізаного конуса 3 дм і 7 дм, твірна 5 дм. Знайдіть площу осьового перерізу.

ІІІ Домашнє завдання

§ 6, п. 56 задачі № 12,13,19,22 (ст.. 96 – 97)

IV Підведення підсумку уроку

Запитання до класу

1. Що є перерізом конуса площиною, яка паралельна основі?
2. Що є перерізом конуса площиною, яка проходить через дві твірні?
3. Що таке зрізаний конус?

Урок – карусель «Квадратні рівняння»

Мета:

● систематизувати знання, уміння і навички учнів про види і методи  розв’язування квадратних рівнянь, перевірити ці знання  та  вміння   застосовувати  їх  при  розв’язуванні  вправ і творчих завдань;

● формувати  вміння  узагальнювати, робити  висновки,  проводити  міркування  по  аналогії, розвивати  логічне  мислення  та  мову  учнів;

● виховувати  розуміння  значимості  алгебри, як  науки  серед  інших  наук, розвивати  комунікативні якості учнів.

Девіз уроку:

Хіба  ти  не  помітив, що  здібний  до  математики  успішний  у  всіх  науках  про  природу? ( Платон )

Обладнання:

Портрети  вчених (Мухаммеда  аль-Хорезмі, Евкліда, Франсуа Вієта, Омара Хайяма), реферати учнів про цих вчених, збірники на кожну парту (1.Дидактичні матеріали для різнорівневого навчання з  алгебри в  8 класі М.А. Капіносова,

2.Алгебра  в  таблицях  для  7-9  класів Т.Г. Роєвої), картки-консультації, картки з записаними на  них  різними  видами  рівнянь, вислови про математику, аркуші ватману, кольорові фломастери.

І. Орг. момент.

 Повідомлення  теми, мети, та девізу  уроку.

ІІ. Активізація опорних знань учнів.

Фронтальне опитування.

1. Яку  тему  ми  зараз  вивчаємо?
2. Що  називається  рівнянням?
3. Що  називається  коренями  або  розв’язками  рівняння?
4. Що  значить  розв’язати  рівняння?
5. Які властивості  рівнянь  ви  знаєте?
6. Які  види  рівнянь  в  залежності  від  степеня  змінної  ви  вже  вмієте  розв’язувати?
7. Що називається  лінійним  рівнянням?
8. Що  називається  квадратним  рівнянням?
9. Які є види квадратних  рівнянь?

ІІІ. Історична  сторінка.

Першим  описав  способи  розв’язування лінійних  рівнянь, схожі  на  ті, якими  ми  користуємося  зараз, Мухаммед аль-Хорезмі

 У  трактаті „Кітаб ал- джебр ал-Мукабала” в ІХ столітті.

(Повідомлення  учнів на  цю  тему).

Способи  розв’язування  квадратних  рівнянь  зустрічаються  ще  в ІІІ ст.. до  н.е. в праці  старогрецького математика  Евкліда „Начала”.

(Повідомлення  учнів на  цю  тему).

Але  праці  давньогрецьких  математиків  були  дуже  громіздкими  і  незручними, тому  що  всі  математичні  перетворення  подавалися  не за  допомогою  символів, а за допомогою  слів.

Велика  заслуга  в  створенні  алгебраїчної  символіки і  вдосконалення  теорії  розв’язування  квадратних рівнянь французького математика Франсуа Вієта.

(Повідомлення  учнів на  цю  тему).

ІV. Систематизація  та  узагальнення  знань  учнів.

1. Метод  „Карусель”.

              Учнів  об’єднуємо  в  гетерогенні (різнорідні  за  рівнем  знань)            групи  по  5 – 6 осіб за  кольором  розданих  вчителем  карток.

В  кожній  групі  розподіляються  обов’язки:

  Спікер – зачитує  завдання  групі, організовує  порядок  виконання  завдання, визначає доповідача, в  кінці  уроку  дає  оцінку  роботи в  класі  а  також  якості  підготовки  до  уроку  кожного члена  групи .

Секретар – веде  записи  результатів  роботи  групи.

Посередник – стежить  за  часом.

Доповідач – чітко  висловлює  думку  групи, доповідає  про  результати  роботи  групи.

Кожній  групі  дається  аркуш  ватману  і  фломастер  такого ж кольору, як  і  їх  картки.

Завдання:

І група – неповні  квадратні  рівняння,

ІІ група – повні  квадратні  рівняння,

ІІІ група – зведені  квадратні  рівняння.

за 1-2 хвилини треба обговорити і записати  схематично  на  аркуші  ватману  означення  даного  рівняння;

1. передати  аркуш  наступній  групі  за  годинниковою  стрілкою  і  на  отриманому  аркуші написати  схематично  першу  частину  формул для  розв’язування  того  типу  рівнянь, який записаний на  тому аркуші, який група отримала  зараз;
2. через установлений час аркуші  знову  передають  за  годинниковою  стрілкою і  кожна  група  повинна  закінчити  записи  формул;
3. коли  до  кожної  групи  повернеться  аркуш  з  її  початковим  завданням, учні  групи  повинні  переглянути  всі  записи,  можливо  доповнити  і  підготуватись  до  виступу;
4. потім  дається  слово  по  черзі  доповідачу  з  кожної  групи і він  розповідає  перед  усім  класом  про  способи  розв’язування  даного  виду  рівнянь, вказує  на  можливі  неточності в  записах, які  зробили  учні  інших  груп. Решта  учнів  слухають, задають  питання.

2)Розв’язування  вправ.

1. Усні  вправи.

На  дошці  прикріплюються  картки  з  записаними  на  них  рівняннями:

1. 2Х² + 3Х + 8 = 0
2. 2Х² + 3Х³  +Х = 0
3. 2Х² + 3 = 0
4. 2Х + 3 = 0
5. 2Х²  = 0
6. Х² + 2Х + 3 = 0
7. 2Х + 3Х² + 8 = 0
8. 2Х² + 3Х = 0

Завдання:

• Серед  записаних  на  дошці  рівнянь  вказати  номери  повних  квадратних  рівнянь.
• Неповних  квадратних  рівнянь.
• Зведених  квадратних  рівнянь.
• Лінійних  рівнянь.
• Рівнянь ІІІ степеня.
• Вказати  значення  коефіцієнтів  в  квадратних  рівняннях.
• Порахувати  квадратами  чисел: 1², 2², 3,²… до 15².

Б. Робота  в  групах – метод „Карусель”.

Учні  виконують завдання  на  великих  аркушах:

І група:

1. 16Х² = 0
2. 4Х² - 8Х = 0
3. 2Х² – 50 = 0

ІІ група:

1. 4Х² + 5Х + 1 = 0
2. 25Х² - 10Х + 1 = 0
3. 5Х² + 2Х + 4 = 0

                ІІІ група:

1. Х² - 7Х + 12 = 0
2. Х² + 7Х - 18 = 0
3. Х² + 2Х - 35 = 0

Після  повного  оберту „каруселі”  учень-доповідач з  кожної  команди розповідає  перед  класом  про  хід  розв’язку  рівнянь.

В. Усний рахунок.

За  збірником  М.А. Капіносова  „Дидактичні  матеріали  для різнорівневого  навчання  з  алгебри  в  8  класі”. (ст.. 28)

Неповні  квадратні  рівняння: вказати  розв’язки:

№100

№101              (вибірково).

№102 

№103

Обчислити  дискримінант  і  вказати  кількість  коренів  рівняння:

№104 (6 рядок). Зведені  квадратні  рівняння: №105 (вибірково).

Г. Творчі завдання. Робота  в  парах.  

1. Скласти  квадратне  рівняння  за  його  коренями: 2 і 7.
2. Скласти  квадратне  рівняння  за  його  коренями: 3 і 5.
3. Рівняння Х² + рХ + 24 = 0 має  корінь Х₁ = 8. Знайти  р і  другий  корінь.
4. Рівняння Х² - 7Х + q = 0 має  корінь Х₁ = 5. Знайти  q і  другий  корінь.
5. При  яких  значеннях  в  рівняння 3Х² + вХ + 12 = 0 має  один  корінь?
6. Визначте підбором  при  яких  цілих  додатних  значеннях  с  рівняння 2Х² + 3Х + с = 0  не  має  розв’язків.
7.  

V. Самостійна  робота  учнів.

За  збірником  Роєвої Т.Г. „Алгебра  у  таблицях”  для  7 – 9 класів. (ст..72)

С – 3 – 1.

Диференційовані  завдання  на  6  варіантів.

Учні  індивідуально  обирають складність  завдання.

Учні, які  самостійно  не  можуть  виконати  завдання, отримують  картку-консультацію з прикладами  розв’язаних  рівнянь. При  цьому  оцінка  за  роботу  знижується.

VI. Підсумок  уроку.

Ми  узагальнили  знання  про  квадратні  рівняння  і  ще  раз  переконалися, що  математика, як  і  будь-яка  інша  наука,  не  розвивається  сама, всі  відкриття  в  ній  роблять  люди.  Так, свій  внесок  в  розвиток  вчення  про  рівняння  зробили  вчені:

• Мухаммед аль-Хорезмі – про способи  розв’язування  лінійних  рівнянь;
• Евклід  і  Франсуа  Вієт  -  про  розв’язування  квадратних  рівнянь.

Але  для  математиків  важливо  було  навчитися  розв’язувати  кубічні  рівняння – адже  куби  -  це  об’єми, а  їх  потрібно  вміти  обчислювати.

Першим, хто  поставив  це  запитання  і  дав  відповідь  на  нього, був  видатний  перський  поет Омар  Хайям.(Повідомлення  учнів на  цю  тему).

Рядками  своїх  віршів  Омар  Хайям  дає  мудрі  поради  на  різні  життєві  ситуації.

Ці  вчені,  про  яких  ми  сьогодні  говорили, не  обмежувалися  лише  математикою, вони  були  високо  освіченими  і  всебічно  розвинутими  в  різних  галузях  науки. До  цього ж  повинні  прагнути  і  ви.

VIІ. Домашнє  завдання.

Для  всіх: №329, №418

Для учнів, які  розв’язували 5-6 варіант - додатково:

Придумати  і  розв’язати  творчі  завдання,  аналогічні  до  тих, які  розв’язували  на  уроці.

Урок – гра «Що? Де? Коли?»

 Додавання і віднімання раціональних чисел

Мета: Узагальнення й систематизація знань про від’ємні числа та дії над ними. Розвивати навички розв’язування вправ і задач, способи і прийоми мислення, індивідуальні здібності учнів, їх пізнавальні інтереси. Виховувати культуру математичних записів, культуру усного і письмового мовлення та міжособистісного спілкування.

Тип уроку: урок узагальнення та систематизації знань учнів.

Хід уроку

Девіз:  “Думати – колективно,

                                                                                                Діяти – оперативно,

                                                    Сперечатись – доказово

                                                                                       Це для всіх обов’язково.”

Вчитель.                

Усі мерщій сідайте, діти,

Домовляймось не шуміти,

На уроці не дрімати,

Руки вчасно піднімати

І щоб не було мороки

Всі готові до уроку

Тож гаразд часу не гаєм

І урок розпочинаємо.

Урок сьогодні - не простий,

Усім відомий, звичний,

Я пропоную провести

Що? Де? Коли? Математичний.

Отож, озбройтеся знаннями

Я сподіваюсь, вдасться вам

Здолати всі перепони

Вперед – в країну чисел раціональних,

Сміливо вирушаємо,

І все, що вивчили раніше,

Давайте, пригадаємо.

     На столі лежать конверти із завданнями для учнів. Пояснюю умови нашої гри. Вибираємо капітана команди. Розпочинаємо гру.

Перший конверт. Усний рахунок. ( Перед кожним учнем знаходиться таблиця “Дії з десятковими та звичайними дробами, додатними та від’ємними числами”).

Отже, ми помітили, що відповідями є від’ємні числа.

Повідомлення учня. Від’ємні числа виникли в Китаї в І ст. до нашої ери. В зв’язку з розв’язанням рівнянь. Додатними числами позначено майно, наявні гроші, прибуток. Їм раділи і зображали їх червоним кольором

( китайці їх називали “чен”), від’ємними числами позначали борг, збиток і зображали їх чорним кольором (їх називали “фу”). В Європі від’ємні числа почали використовувати, починаючи з 12 ст. Однак, ставились до від’ємних чисел з недовірою, називаючи їх “фіктивними”, “абсурдними”, “хибними”. Тільки в 12 ст. коли видатний французький математик Рене Декарт (1596-1650 р) запропонував від’ємні і додатні числа зображати точками координатної прямої, від’ємні числа були повністю визнані і стали повноправними атрибутами математики.

Другий конверт. Математичний диктант

1. Чому дорівнює сума чисел –7 і –5?
2. Знайти суму чисел –2,5 і 14,5.
3. Чому дорівнює сума модулів чисел –9 і –3?
4. Закінчити речення : “ Щоб від числа х відняти число 12, потрібно до числа х додати число …?
5. Знайти різницю – 4 відняти 8.

 (Вчитель зачитує правильні відповіді, а учні олівцями відмічають правильні і неправильні відповіді. Проводиться самооцінювання).

Третій конверт. Закінчити речення.

- (-2) =                                                                                      - (+5) =

- (- ) =                                                                                       - (+ ) =

Ворог мого ворога - мій… ( товариш)  Ворог мого товариша – мій ..(ворог)

+(-7) =                                                                                       +(+11) =

+(- ) =                                                                                        +(+ ) =

Товариш мого ворога-мій(ворог)   Товариш мого товариша – мій (товариш)

Вчитель. Такі речення ми використовуємо сьогодні у своїй мові. Але правила дій знали ще й раніше. Індійські математики Брахмагупта

 (7 ст.н.е) і Бхаскара (12 ст.н.е) склали правила дій для від’ємних і додатних чисел:

“Сума майна і майна є майно”.

“Сума боргів є борг”.

“Сума майна і боргу дорівнює їх різниці”.

“Сума майна і такого самого боргу дорівнює нулю”.

“Добуток боргу на борг є майно”.

Четвертий конверт. Розв’язати задачу.

“Мале підприємство заборгувало  банку 17 000 грн., через деякий час ще заборгувало 5 000 грн. Потім  поклало на рахунок 34 000 грн. Чи має підприємство на рахунку в банку гроші? Якщо має, то скільки?”

Учень. Історична довідка про гривню.

У наших пращурів від середини 11 ст. побутували злитки зі срібла певної ваги та форми, так звані гривні. Гривня – зливок срібла, маса якої приблизно дорівнює фунту (0,4095 кг). Гривні не були однакові в різних містах. В Києві – плоскі, шестикутні, у Чернігові – плоскі й півкруглі з розплющеними кінцями. Вартість гривень визначалась їхньою вагою. Це була срібна гривня(вагова). Певне число срібних монет складало гривню кун. Найпоширенішими були гривні трьох типів: київська, чернігівська, новгородська. Іноді зустрічались литовські й татарські. Вони відрізнялись своєю формою і вагою. Для господарств Південне –Західної Русі були характерними золоті гривні (злитки). Вони служили засобом накопичення і використовувалися  лише у великих торговельних операціях купецькими корпораціями. У другій половині XIII cт. гривню почали рубати навпіл і назвали рублем.

 П’ятий конверт. Розв’язати рівняння.( Групова робота).

-7+ х= -19;                  ( х + 7) – 19 = - 24;             І х – 3 І + 6 = 15.

Вчитель.  Зверніть увагу на корені рівнянь.

Учень. Певну інформацію про грошовий обіг на території Київської Русі містить унікальний звід законів стародавніх часів – “ Руська правда” ( ХІ- ХІІ ст.).

     Якщо холоп ударив вільного чоловіка, а пан почне ховати його, то мусить заплатити за холопа 12 гривень. А якщо забере чужого холопа чи раба, платити йому за образу 12 гривень.

Шостий конверт. Самостійна робота. ( Учням роздаються диференційовані завдання. Перевірка здійснюється шляхом передачі завдань по номерах).

Сьомий конверт. Домашнє завдання.( Пишеться на дошці.)

Восьмий конверт. Підсумок уроку.

Вчитель. Підсумок уроку підведе капітан команди, розповівши правила додавання і віднімання раціональних чисел. Якщо відповідь правильна, то хлопають в долоні. Зверніть увагу на відповіді задачі і рівнянь. Число 12.Чому? Бо в світі по 12 є всього доволі: 12 місяців, 12 сузір’їв, 12 учнів у Христа, 12 цифр на циферблаті, сервіз на 12 персон, 12 пісних страв на Святвечір, 12 років  в школі треба відходити з оцінкою 12.

   Виставлення і коментування оцінок. Вручення приза капітану команди -дерев’яна сова.

Дев’ятий конверт.

Музикальна пауза.

Розв’язав Петрусь задачу,

Тільки мінуса не бачив,

От і сталось, що лимон

Важить майже 8 тон.

На контрольній ловив гав,

Одиницю упіймав,

Підглядав у всі книжки,

Переплутав сторінки.

Хоч сідай та гірко плач:

Не люблю отих задач!

Через них одні невдачі

Ох! Замучили задачі!

Вчитель.   Бажаю математику

                    Вам вчити добре й далі,

                   Так, щоб усі могли отримати

                    Срібні й золоті медалі.

5. Висновки

Система класних і позакласних самостійних робіт повинна:

• бути єдиною для самостійних робіт як у класі, так і вдома;
• забезпечувати активну пізнавальну діяльність на всіх етапах навчання та сприяти розв’язанню тих конкретних задач, які ставляться на даному етапі;
• задовольняти основним принципам дидактики;
• навчальні завдання, які входять у самостійну роботу, повинні забезпечувати формування в учнів не тільки основ науки яка вивчається , але й навичок самоосвіти;
• характер навчальної діяльності повинен визначитися системою навчальних завдань, які входять до системи самостійних робіт та відповідати відповідному методу навчання: репродуктивному, частково пошуковому, дослідницькому;
• система навчальних завдань повинна задовольняти вимозі послідовного наростання труднощів.

Система самостійних робіт повинна бути розроблена на основі:

• змісту навчального курсу, розділу або теми предмету, який вивчається;
• загальних засобів та методів активізації навчального процесу (методів навчання, прийомів навчальної роботи, видів навчально-пізнавальної діяльності, засобів навчання);
• характеристик, залежних від завдань, які складають самостійну роботу (склад їх компонентів, ступінь складності, послідовність розміщення).

В своїй роботі користуюсь перш за все методом проблемного навчання і формування творчих здібностей учнів. Невід'ємною частиною цього методу є евристична бесіда, під час якої, під керівництвом вчителя, учні проходять весь шлях пошуку нового знання аж до його відкриття, а саме: створювали умови для виникнення проблемної ситуації, спонукали учнів сформулювати проблему, керувалися самим процесом пошуку (ставили допоміжні запитання, стимулювали учнів до спостережень, порівняння, застосування раніше здобутих знань у новій ситуації, контрприклади), спонукали до формування висновку, (а якщо є потреба, коректували висновок). Таку бесіду з учнями проводили за наперед заготовленим і записаним на дошці планом, в якому вказано сторінку у підручнику, абзац, тощо. Отже, учні вчаться самостійно здобувати знання. А всілякі запитання вчителя дають змогу добитися усвідомлення учнями вивченого.

Доведено, що дитина розвиватиметься, вдумливо працюватиме, збагачуватиме свої пам'ять і фантазію, якщо завдання, які вона виконує на уроках будуть цікавими. Тому пропонували учням вправи, які не потребують додаткових знань, але, маючи пошуково-проблемний характер, вчать порівнювати, аналізувати, співставляти з протиставленням, встановлювати деякі математичні закономірності.

6. Список використаних джерел

1. Г.П. Бевз. Методика викладання  математики . – К., „Вища школа” 1989 – 367с.
2. Методика викладання математики : Практикум/під редакцією Г.П.Бевза/. -К.: „Вища школа” , 1981-198с.
3. Г.П.Бевз. Методика викладання математики. Загальні питання,-К.: „Радянська школа”, 1968-195с.
4. Освітні технології: Навчально – методичний посібник, О.М.Пєхота та ін., -К.:А. С. К, 2004 -256с.
5. О. Пометун. Сучасний урок. Інтерактивні технології навчання.- К.: Видавництво А.С. К., 2004,-192с.
6. Урок математики в сучасних технологіях: теорія і практика. (Уклад І.С. Маркова. – Х.: „Основа” 2007.-144с- (Б-ка тури. „Математика в школах України”., Випуск 9(57)
7. В.М. Козира. Технологія уроку з математики. – Т.: Астон, 2002-52с.
8. Я.С. Бродський. Математика: Тести для самостійної роботи та контролю знань. – Т.: Навчальна книга- Богдан, 2007-160с.
9. В.Ф. Чучуков. Математичні диктанти . – К.: Радянська школа, 1985-64с.