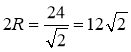ЗАБЕЗПЕЧЕННЯ БЕЗПЕРЕРВНОГО НАВЧАННЯ МАТЕМАТИКИ ШЛЯХОМ ВПРОВАДЖЕННЯ ЕЛЕМЕНТІВ ДИСТАНЦІЙНОГО НАВЧАННЯ

ЗАБЕЗПЕЧЕННЯ БЕЗПЕРЕРВНОГО НАВЧАННЯ МАТЕМАТИКИ
ШЛЯХОМ ВПРОВАДЖЕННЯ ЕЛЕМЕНТІВ ДИСТАНЦІЙНОГО НАВЧАННЯ
Пістинь,
2021 рік

ЛАВРУК
Василь Миколайович,
директор
Пістинського ліцею
Косівської міської ради Івано-Франківської області,
вчитель математики
Стаж – 30 років;
Освіта – вища (Прикарпатський університет ім..В.Стефаника, 1996 рік;
Тернопільський національний педагогічний університет ім..В.Гнатюка, 2010 рік);
Категорія – вища;
Звання «Старший вчитель».
«Освіта — це та сфера людської діяльності, яка є фундаментом або розвитку суспільства, або його деградації».
Є. С. Полат
 ПРОБЛЕМНА СИТУАЦІЯ 1
ПРОБЛЕМНА СИТУАЦІЯ 1
Дитина захворіла. З ким не буває? Пропускає школу. Поступово їй стає краще, але відвідувати школу лікарі ще не дозволяють. Можна дізнатися, що проходили в класі, але не завжди учень може сам розібратися з новим матеріалом. Як бути?
 ПРОБЛЕМНА СИТУАЦІЯ 2
ПРОБЛЕМНА СИТУАЦІЯ 2
У школі, селі, регіоні тощо — епідемія. Лікарі оголошують карантин. Відвідувати школу небезпечно для здоров'я. Оголошують позачергові канікули.
 ПРОБЛЕМНА СИТУАЦІЯ 3
ПРОБЛЕМНА СИТУАЦІЯ 3
У школі немає вчителя математики тощо. Просити вчителя фізкультури узяти на себе викладання предмета? Можливо, не атестувати учнів із предмета, тобто визнати пропуск в їхній освіті?
 ПРОБЛЕМНА СИТУАЦІЯ 4
ПРОБЛЕМНА СИТУАЦІЯ 4
У сім'ї є дитина-інвалід. Вона за станом здоров'я не може відвідувати школу, але здобути освіту дитині необхідно. Як це зробити?
 ПРОБЛЕМНА СИТУАЦІЯ 5
ПРОБЛЕМНА СИТУАЦІЯ 5
Екстернат. Профільне навчання. Дистанційне навчання (ДН) — це одна із форм організації освітнього процесу, за якої всі або частина занять здійснюється з використанням сучасних інформаційних і телекомунікаційних технологій під час територіальної віддаленості вчителя й учнів. Навчання в старших класах з окремими предметами профільної спрямованості робить акцент на самостійній діяльності учнів. Як?
 ПРОБЛЕМНА СИТУАЦІЯ 6
ПРОБЛЕМНА СИТУАЦІЯ 6
У класі, школі є особливо обдаровані діти або діти, які просто виділяються в розвитку серед інших учнів. їм буває нудно на уроках. Хотілося б заглибитися в детальне вивчення предметів, що цікавлять. Але як?
Таких ситуацій, що призводять до істотних проблем соціального, а потім і державного масштабу, можна перерахувати багато. Наприклад робота з тими, хто відстає, або, навпаки, з обдарованими дітьми, додаткова освіта. Дистанційне навчання у школі дає можливість вивести на новий рівень допрофільну й профільну підготовку учнів, забезпечити гнучкість та багатоваріантність у навчанні, сприяє розкриттю учнівського потенціалу.
 Саме дистанційна форма навчання відкриває можливості для учнів, які пропускають школу з поважних причин (через змагання, конкурси, хвороби, перебування за кордоном тощо), та особливо для тих, хто за станом здоров'я навчається індивідуально, якісно задовольнити власні потреби в здобутті освіти.
Саме дистанційна форма навчання відкриває можливості для учнів, які пропускають школу з поважних причин (через змагання, конкурси, хвороби, перебування за кордоном тощо), та особливо для тих, хто за станом здоров'я навчається індивідуально, якісно задовольнити власні потреби в здобутті освіти.
![0001ah81[1].jpg](/uploads/files/1985556/228964/244934_html/images/228964.005.png) Дистанційні технології навчання можна розглядати як природний етап еволюції традиційної системи освіти від дошки з крейдою до електронної дошки й комп'ютерних навчальних систем, від книжкової, бібліотеки до електронної, від звичайної аудиторії до віртуальної.
Дистанційні технології навчання можна розглядати як природний етап еволюції традиційної системи освіти від дошки з крейдою до електронної дошки й комп'ютерних навчальних систем, від книжкової, бібліотеки до електронної, від звичайної аудиторії до віртуальної.
 Дистанційне навчання — нова форма освітнього процесу, що передбачає самостійне навчання учня як основний спосіб здобуття знань, а також і сукупність інформаційних технологій, що забезпечують учня доступом до основного обсягу навчального матеріалу, інтерактивну взаємодію учнів та вчителів у процесі навчання. Дистанційне навчання учнів стане ефективним за умови забезпечення відповідних організаційно-педагогічних умов, а саме: теоретичного обґрунтування і дотримання дидактичних принципів дистанційного навчання; спрямованості процесу навчання учнів на формування їхніх життєвих компетентностей; забезпечення можливостей для вдосконалення комунікативних умінь учнів; створення та практичного впровадження моделі педагогічної взаємодії учасників освітнього процесу шляхом інтеграції традиційної і дистанційної форм навчання.
Дистанційне навчання — нова форма освітнього процесу, що передбачає самостійне навчання учня як основний спосіб здобуття знань, а також і сукупність інформаційних технологій, що забезпечують учня доступом до основного обсягу навчального матеріалу, інтерактивну взаємодію учнів та вчителів у процесі навчання. Дистанційне навчання учнів стане ефективним за умови забезпечення відповідних організаційно-педагогічних умов, а саме: теоретичного обґрунтування і дотримання дидактичних принципів дистанційного навчання; спрямованості процесу навчання учнів на формування їхніх життєвих компетентностей; забезпечення можливостей для вдосконалення комунікативних умінь учнів; створення та практичного впровадження моделі педагогічної взаємодії учасників освітнього процесу шляхом інтеграції традиційної і дистанційної форм навчання.
 Основні завдання:
Основні завдання:
• вивчити та узагальнити досвід із теми;
• створити організаційно-педагогічні умови впровадження дистанційного навчання;
• розробити й теоретично обґрунтувати модель інформаційного паспорта навчальної теми;
• розробити методичні рекомендації щодо впровадження дистанційного навчання школярів;
• узагальнити отримані результати.
Інноваційні підходи до викладання у школі вимагають від сучасного вчителя нових форм організації безперервного навчання. Однією з таких форм є дистанційне навчання, що змінює уявлення про просторово-часові функції організації процесу учіння. Впровадження дистанційного навчання стало одним із основних у системі безперервної освіти, бо є природним етапом еволюції традиційної системи освіти від дошки з крейдою до комп'ютерних навчальних систем, від книжкової бібліотеки до електронної, від звичайної аудиторії до віртуальної.
![0001ah81[1].jpg](/uploads/files/1985556/228964/244934_html/images/228964.008.jpg) Головним завданням дистанційного навчання є розвиток творчих та інтелектуальних здібностей людини за допомогою відкритого і вільного використання всіх освітніх ресурсів і програм, у тому числі, доступних в Інтернеті. А оскільки Інтернет – це світова інформаційна мережа, то вона може бути одним із засобів дистанційного навчання, тому що її дані допоможуть учням (і вчителям) створити повну інформаційну картину з питань, що їх цікавлять.
Головним завданням дистанційного навчання є розвиток творчих та інтелектуальних здібностей людини за допомогою відкритого і вільного використання всіх освітніх ресурсів і програм, у тому числі, доступних в Інтернеті. А оскільки Інтернет – це світова інформаційна мережа, то вона може бути одним із засобів дистанційного навчання, тому що її дані допоможуть учням (і вчителям) створити повну інформаційну картину з питань, що їх цікавлять.
Принципи дистанційного навчання:
- доступність навчання, а саме подолання фізичних обмежень людини, розширення аудиторії учнів;
- індивідуальна спрямованість навчання, створення комфортних умов для школярів і вчителів, урахування індивідуальних психологічних особливостей (сприйняття, пам’яті, мислення), індивідуальний темп навчання;
- розвиток інформаційної культури, навичок роботи із сучасними засобами інформатизації і телекомунікації;
- соціалізація навчання, урахування особистісно-комунікативних особливостей учнів.
-
 На мою думку, реалізація дистанційного навчання є корисним, оскільки воно дозволить розв’язати низку завдань, які можна сформулювати так:
На мою думку, реалізація дистанційного навчання є корисним, оскільки воно дозволить розв’язати низку завдань, які можна сформулювати так:
- забезпечення доступності різноманітних навчальних ресурсів;
- здобування повної загальної середньої освіти в зручній, адекватній і відповідній формі для того, хто навчається;
- важливість для психологічного розвитку дитини – його залучення в систематичну освітню діяльність під безпосереднім керівництвом дорослого, процес володіння культурою і соціалізація проходять за допомогою вчителя;
- розвиток творчих та інтелектуальних здібностей дитини за допомогою відкритого і вільного використання всіх освітніх ресурсів і програм, у тому числі, доступних в Інтернеті;
- обмін даними, комунікативна діяльність на базі спільних інтересів, перш за все освітніх;
- сприяння розвитку профільної освіти у школі;
- організація дозвілля, відпочинку і розвитку.
Основними перевагами дистанційного навчання є: екстериторіальність, синхронний і асинхронний режими взаємодії учасників навчального процесу: викладач – учень, учень – учень, учень – навчальна група; можливість залучення до навчання спеціалістів із певних галузей; одночасне з вивченням інших предметів практичне засвоєння інструментів ІКТ – створення додаткових умов для впровадження ІКТ в освітні системи тощо.
 Розуміючи дистанційне навчання не тільки як педагогічну технологію, але і як соціальну практику, треба підкреслити, що воно сприяє здійсненню модернізаційної трансформації комунікативних процесів у школі. До загальноосвітніх навчальних закладів, елементи дистанційного навчання прийшли з вищої школи. Прикладом є роботи П.Глотцом і Д.Зимоном про ефективність вищої освіти, заснованої на дистанційному навчанні. Специфіка праць вищезазначених практиків розкриває шляхи трансформації комунікативних процесів у західноєвропейських університетах. П.Глотц пише: "15-20% навчального плану справді може здійснюватися інтерактивно й за допомогою сучасних засобів, як online, так і offline. Це сприяло б оптимізації й раціоналізації процесів навчання і викладання. Я не підтримую ідеї, що в цих процесах можна цілком виключити особисті контакти. Разом з тим частину занять можна провадити за допомогою електронної пошти. Д.Зимон вважає, що дистанційне навчання – це прообраз нової організації системи освіти за принципом екстериторіальності й деінституалізаці .
Розуміючи дистанційне навчання не тільки як педагогічну технологію, але і як соціальну практику, треба підкреслити, що воно сприяє здійсненню модернізаційної трансформації комунікативних процесів у школі. До загальноосвітніх навчальних закладів, елементи дистанційного навчання прийшли з вищої школи. Прикладом є роботи П.Глотцом і Д.Зимоном про ефективність вищої освіти, заснованої на дистанційному навчанні. Специфіка праць вищезазначених практиків розкриває шляхи трансформації комунікативних процесів у західноєвропейських університетах. П.Глотц пише: "15-20% навчального плану справді може здійснюватися інтерактивно й за допомогою сучасних засобів, як online, так і offline. Це сприяло б оптимізації й раціоналізації процесів навчання і викладання. Я не підтримую ідеї, що в цих процесах можна цілком виключити особисті контакти. Разом з тим частину занять можна провадити за допомогою електронної пошти. Д.Зимон вважає, що дистанційне навчання – це прообраз нової організації системи освіти за принципом екстериторіальності й деінституалізаці .
Актуальною є думка Г.Гізеке про соціальну зумовленість освіти, яку, незважаючи на її очевидність, часто ігнорують. Дослідник зазначає, що освіта, – інституалізується суспільством передусім у своїх власних цілях, а не в цілях тих, хто навчається, якими б вони не були. Те, що сьогодні учень з його інтересами і потребами особливо наполегливо висувається в центр педагогічного мислення, є просто-напросто варіацією споконвічного й насправді незмінного суспільного договору. Суспільству потрібна індивідуалізація, здатність до безперервного навчання, а також уміння справлятися з перспективами, здатним викликати ризик, і суперечливими очікуваннями .
 Система дистанційного навчання є програмно-апаратним комплексом, призначеним для управління освітнім процесом із застосуванням мережних комунікаційних технологій з метою надання освітніх послуг широкому колу населення. Найбільш важливими компонентами дистанційного навчання є: створення практичних ситуацій під час навчального процесу, можливість проявити себе, самореалізуватися, чіткість організації навчального процесу, індивідуального підходу.
Система дистанційного навчання є програмно-апаратним комплексом, призначеним для управління освітнім процесом із застосуванням мережних комунікаційних технологій з метою надання освітніх послуг широкому колу населення. Найбільш важливими компонентами дистанційного навчання є: створення практичних ситуацій під час навчального процесу, можливість проявити себе, самореалізуватися, чіткість організації навчального процесу, індивідуального підходу.
В ході дистанційного навчання слід враховувати і психологічні процеси особистості. Вчителю необхідно звернути увагу на психологічні закономірності сприйняття, пам'яті, мислення, уваги, а також вікові особливості учнів. Врахування цих особливостей сприяє підвищенню рівня сприйняття інформації й засвоєння навчального матеріалу школярами. Учасники дистанційного навчання повинні розуміти призначення запропонованих курсів, планувати роботу, яка базується на інтерактивності освітнього процесу.
Другий атрибут психологічного комфорту в процесі навчання досягається зворотним зв'язком між учнем і вчителем, що полягає в міжособистісному спілкуванні. Крім важливого чинника – культури спілкування, важливим є подача інформації. Інформація повинна бути точно-підібраною та розкривати зміст теми у повному обсязі, спонукати учнів до здобуття нових знань та забезпечувати інтерактивність .
Для успішної організації дистанційного навчання, важливим є вміння працювати в навчальному сервері, знати різноманітні ресурси, користуватися електронною поштою, мати телефонний і факсимільний зв'язок, долучатися до відеоконференцій та інше.
Інформаційний паспорт навчальної теми з геометрії,
10 клас
«Перпендикулярність прямих і площин у просторі»






За Програмою для загальноосвітніх навчальних закладів, яка затверджена наказом Міністерства освіти і науки України № 408 від 20.04.2018 року «Про затвердження типової освітньої програми закладів загальної середньої освіти ІІІ ступеня, 10 класи».
Джерело:https://www.pedrada.com.ua/news/4612-zatverdjeno-tipov-osvtn-programi-novo-ukransko-shkoli
Тема №2, геометрія 10 клас.
Частина 1.
У частині 1 (таблиця 1.1) наведено джерела інформації, за якими учень може самостійно вивчати тему. Для їх вивчення використано перелік підручників, навчальних посібників, які рекомендовані Міністерством освіти і науки України на 2018/2019 навчальний рік. Крім цього до частини включено джерела, рекомендовані для розширення та поглиблення знань з відповідної теми.
Перелік джерел навчальної інформації
Таблиця 1.1
|
№ з/п |
Вид |
Назва |
Автори |
Видав-ництво |
Рік ви-дан-ня |
|||
Міністерством освіти і науки України |
||||||||
|
1 |
Підручник |
Математика, 10 клас (алгебра і початки аналізу та геометрія, рівень стандарту) |
Бурда М.І., Колесник Т.В, Тарасенкова Н.А |
К., Оріон |
2018 |
|||
|
2 |
Підручник |
Математика (алгебра і початки аналізу та геометрія), 10 клас |
Мерзляк А.Г., Номіровський Д.А., Полонський В.Б. |
Х., Гімназія |
2018 |
|||
|
2. Додаткові підручники та навчальні посібники, рекомендовані Міністерством освіти і науки України |
||||||||
|
3 |
Підручник |
Математика, 10 клас (алгебра і початки аналізу та геометрія, рівень стандарту) |
Нелін Є.П. |
Х., Ранок |
2018 |
|||
|
4 |
Підручник |
Математика, 10 клас (алгебра і початки аналізу та геометрія, рівень стандарту) |
Істер О.С. |
К,. Генеза |
2018 |
|||
|
5 |
Підручник |
Геометрія, 10 клас (Профільний рівень) |
Істер О.С., Єргіна О.В. |
К., Генеза |
2018 |
|||
|
6 |
Підручник |
Геометрія, 10 клас (Профільний рівень) |
Мерзляк А.Г., Номіров-ський Д.А., Полонський В.Б. |
Х., Гімназія |
2018 |
|||
|
7 |
Збірник |
Математика. 10 клас. Збірник самостійних та контрольних робіт. |
Корнес А.І., Бабенко С.П. |
Ранок |
2018 |
|||
|
3. Додаткові джерела інформації в пошуковій системі |
|||
|
https://bila.km.ua/uchnyam-v.../10-klas/.../menu-id-763.html |
https://www.youtube.com/watch?v=C_D40UwH1Gw
|
https://www.youtube.com/watch?v=VQXuTjxK8jw
|
|
Поради, щодо опрацювання деяких джерел з таблиці 1.1:
- Для початкового ознайомлення з теоретичним матеріалом скористайся підручниками, зазначеними в пунктах 1 та 2.
- Для узагальнення та перевірки знань із теми перегляньте посібники, зазначені в пунктах 5-6, та збірник, зазначений у пункті 7.
Частина 2
Рекомендації для вивчення теми
- 1 Загальна характеристика теми
Під час вивчення теми відбувається узагальнення та систематизація знань учнів з планіметрії – розділу, що вивчає взаємне розташування прямих і площин в просторі (розглядається перпендикулярність прямих та площини, двох площин тощо).
Окрім того, учні вивчають теореми про взаємозв’язок паралельності та перпендикулярності прямих та площин у просторі, а також опановують знання про перпендикуляр та похилі тощо.
Тема є практичною (під час вивчення істотно підвищується роль задач на обчислення) та пропедевтичною (для опанування понять кутів у просторі та багатогранників), а також відіграє помітну роль у формуванні просторових уявлень учнів і розвитку конструктивності їхнього мислення.
У таблиці 2.1 подано витяг з навчальної програми щодо змісту
навчального матеріалу з теми та вимог до навчальних досягнень учнів із
їх засвоєння.
Таблиця 2.1
|
Зміст навчального матеріалу |
Навчальні досягнення учнів |
|
Тема №4 «Перпендикулярність прямих і площин у просторі» Перпендикулярність прямих у просторі. Перпендикулярність прямої і площини. Ознака перпендикулярності прямої і площини. Перпендикуляр і похила. Теорема про три перпендикуляри. Перпендикулярність площин. Ознака перпендикулярності площин. Залежність між паралельністю та перпендикулярністю прямих і площин. Кути у просторі: між прямими , між прямою і площиною, між площинами. Відстані у просторі: від точки до прямої, від точки до площини, від прямої до паралельної їй площини (від точки до фігури), між паралельними площинами, між мимобіжними площинами, (між двома фігурами). Ортогональне проектування. (Площа ортогональної проекції многокутника). Практичне застосування властивостей паралельності та перпендикулярності прямих і площин. |
Учень (учениця):
|
- Поради щодо вивчення теми
Зверніть особливу увагу на ознаки перпендикулярності прямої та площини, теорему про три перпендикуляри та ознаку перпендикулярності площин. Доведення ознаки перпендикулярності прямої та площини спирається на логічні й геометричні зв язки та відношення між планіметричними фігурами, розташованими у тривимірному просторі.
Не забувайте , що під час вивчення теореми про три перпендикуляри необхідно довести і першу, і другу частини теореми, а також розібрати її на малюнках, якщо в основі лежить прямокутний, рівнобедрений та довільний трикутники.
Зверніть увагу на використання теореми Піфагора і насідків з неї в ході розв язування задач на похилу.
- Словник до теми
Визначення основних понять, які зустрічаються в процесі вивчення теми, подано за виданням:
Пряма називається перпендикулярною до площини, якщо вона перетинає цю площину і перпендикулярна до будь-якої прямої, яка лежить у площині і проходить через точку перетину.
Теорема (ознака перпендикулярності прямої і площини).
Якщо пряма, яка перетинає площину, перпендикулярна до двох прямих цієї площини, що проходять через точку перетину, то вона перпендикулярна до площини.
Перпендикуляром, проведеним з даної точки до даної площини, називається відрізок, що сполучає дану точку з точкою площини і лежить на прямій, перпендикулярній до площини.
Теорема (властивості перпендикуляра і похилої).
Якщо з точки, взятої поза площиною, проведені до площини перпендикуляр і похилі, то:
- перпендикуляр коротший за будь-яку похилу;
- проекції рівних похилих рівні і, навпаки, похилі, що мають рівні проекції, рівні;
- з двох похилих більша та, проекція якої більша.
Теорема (про три перпендикуляри).
Якщо пряма, проведена на площині через основу похилої, перпендикулярна до її проекції, то вона перпендикулярна і до самої похилої.
Теорема (обернена до теореми про три перпендикуляри).
Якщо пряма, проведена на площині через основу похилої, перпендикулярна до похилої, то вона перпендикулярна і до проекції похилої.
Теорема (про паралельні прямі та перпендикулярну площину).
Якщо площина перпендикулярна до однієї з двох паралельних прямих, то вона перпендикулярна і до другої.
Теорема (про паралельні площини та перпендикулярну пряму).
Якщо пряма перпендикулярна до однієї з паралельних площин, то вона перпендикулярна і до другої.
Кутом між площинами , які перетинаються, називається кут між прямими, проведеними в цих площинах зі спільної точки перпендикулярно до лінії їх перетину.
- Інформація для запам`ятовування.
Дві прямі називаються перпендикулярними, якщо вони перетинаються під прямим кутом.
Якщо дві прямі, які перетинаються, паралельні відповідно двом іншим перпендикулярним прямим, то інші прямі теж перпендикулярні.
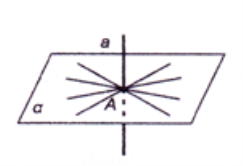 Через будь-яку точку прямої в просторі можна провести безліч перпендикулярних до неї прямих. (Усі прямі лежать у площині, яка перпендикулярна до даної прямої та перетинає її у даній точці.)
Через будь-яку точку прямої в просторі можна провести безліч перпендикулярних до неї прямих. (Усі прямі лежать у площині, яка перпендикулярна до даної прямої та перетинає її у даній точці.)
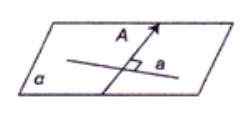 Через будь-яку точку в просторі, що не належить даній прямій, можна провести пряму, перпендикулярну до даної, і тільки одну. Це буде та перпендикулярна до даної прямої пряма, яка лежить у площині, визначеній даними прямою й точкою.
Через будь-яку точку в просторі, що не належить даній прямій, можна провести пряму, перпендикулярну до даної, і тільки одну. Це буде та перпендикулярна до даної прямої пряма, яка лежить у площині, визначеній даними прямою й точкою.
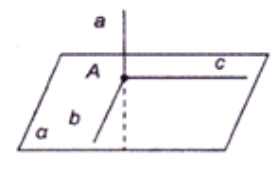 Зверніть увагу, що в просторі дві прямі, перпендикулярні до однієї і тієї самої прямої, необов язково паралельні між собою.
Зверніть увагу, що в просторі дві прямі, перпендикулярні до однієї і тієї самої прямої, необов язково паралельні між собою.
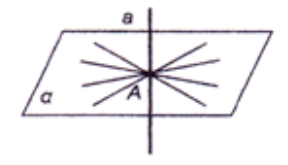 Пряма, яка перетинає площину, називається перпендикулярною до цієї площини, якщо вона перпендикулярна до будь-якої прямої, що лежить у цій площині й проходить через точку перетину.
Пряма, яка перетинає площину, називається перпендикулярною до цієї площини, якщо вона перпендикулярна до будь-якої прямої, що лежить у цій площині й проходить через точку перетину.
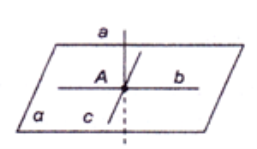 Пряма, яка перетинає площину, називається перпендику-лярною до цієї площини, якщо вона перпендикулярна до будь-якої прямої, що лежить у цій площині й проходить через точку перетину.
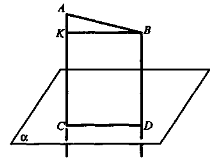
Пряма, яка перетинає площину, називається перпендику-лярною до цієї площини, якщо вона перпендикулярна до будь-якої прямої, що лежить у цій площині й проходить через точку перетину. 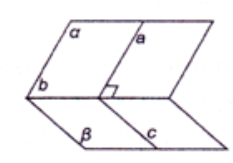 На рисунку a перпендикулярна до площини, але a не перпендикулярна до d , зокрема не перпендикулярна до c .
На рисунку a перпендикулярна до площини, але a не перпендикулярна до d , зокрема не перпендикулярна до c .
Через дану точку площини можна провести одну, й тільки одну, перпендикулярну до неї пряму.
Через дану точку прямої можна провести одну, й тільки одну, перпендикулярну до неї площину.
Через точку, яка не лежить на прямій, можна провести одну, й тільки одну, площину, перпендикулярну до даної прямої.
Якщо площина перпендикулярна до однієї з двох паралельних прямих, то вона перпендикулярна й до другої.
 Дві прямі, перпендикулярні до однієї й тієї ж площини, паралельні.
Дві прямі, перпендикулярні до однієї й тієї ж площини, паралельні.
Частина 3
Додаткові навчальні матеріали
Для вивчення теми рекомендовано використати додаткові навчальні матеріали. Їх подано, як додатки, перелічено в таблиці 3.1 і розміщено на ком пакт-диску.
|
Номер додатка |
Назва додатка |
|
Додаток 3.1 |
Двогранний кут (презентація у форматі Mikrosoft Office Power Point) www.10minclass.com/video/885 |
|
Додаток 3.2 |
Опорний конспект з теми (презентація у форматі Mikrosoft Office Power Point) |
|
Додаток 3.3 |
Опорний конспект уроку узагальнення та систематизації знань з теми (презентація у форматі Mikrosoft Office Power Point), тести онлайн https://videouroki.net/tests/pierpiendikuliarnost-priamykh-i-ploskostiei.html |
|
Додаток 3.4 |
Відеопрезентація з теми (у форматі Movie Maker) https://videouroki.net/tests/geometria/?uc=679&uct=43748 |
Частина 4
Самоперевірка знань
Для самоперевірки набутих учнем знань наведено контрольну роботу. (Додаток 4.1)
Частина 5
Творчі роботи
Для поглибленого вивчення теми пропонується підготувати такі реферати:
- Перпендикулярність прямих і площин у архітектурі.
- Застосування прямих і площин у народній творчості (ковані вироби, дерев яне начиння та прикраси).
- Застосування перпендикулярних прямих та площин у ювелірному виробництві та медицині (оброблення ювелірних виробів, напівдорогоцінних та дорогоцінних каменів).
- Застосування перпендикулярності прямих та площин у техніці.
- Застосування перпендикулярності прямих та площин у деревообробній та металургійній промисловості.
Частина 6
Джерела методичної інформації
У таблиці 6.1 наведено джерела інформації методичного характеру, визначені та рекомендовані для використання вчителем у висвітленні теми.
(Таблиця 6.1)
|
№з/п |
Вид |
Назва |
Автори |
Видав-ництво |
Рік видан-ня |
|||
|
|
||||||||
|
1. Джерела інформації, рекомендовані автором |
||||||||
|
1 |
Посібник |
Майстер-клас. Геометрія. 10 клас (академічний рівень) |
Корнієн-ко Т.А., Фіготіна В.І. |
Ранок |
2010 |
|||
|
2 |
Посібник |
Тести зі стереометрії онлайн |
Брод-ський Я.С. |
ТМ «Розум-ники» |
2017 |
|||
|
3 |
Комплект |
Математика. Довідник +Тести, підготовка доДПА, ЗНО |
Істер О.С. |
К,. Генеза |
2018 |
|||
Частина 7
Додаткові методичні матеріали У таблиці 7.1 запропоновано додаткові методичні матеріали, які можуть бути використані у навчальній роботі. Їх розміщено у формі додатків до частини 7.
|
Номер додатку |
Назва додатку |
|
Додаток 7.1 |
Методичні картки уроків |
(Додаток 2.1).
Пряма називається перпендикулярною до площини, якщо вона перетинає цю площину і перпендикулярна до будь-якої прямої, яка лежить у площині і проходить через точку перетину.
Теорема (ознака перпендикулярності прямої і площини).
Якщо пряма, яка перетинає площину, перпендикулярна до двох прямих цієї площини, що проходять через точку перетину, то вона перпендикулярна до площини.
Перпендикуляром, проведеним з даної точки до даної площини, називається відрізок, що сполучає дану точку з точкою площини і лежить на прямій, перпендикулярній до площини.
Теорема (властивості перпендикуляра і похилої).
Якщо з точки, взятої поза площиною, проведені до площини перпендикуляр і похилі, то:
- перпендикуляр коротший за будь-яку похилу;
- проекції рівних похилих рівні і, навпаки, похилі, що мають рівні проекції, рівні;
- з двох похилих більша та, проекція якої більша.
Теорема (про три перпендикуляри).
Якщо пряма, проведена на площині через основу похилої, перпендикулярна до її проекції, то вона перпендикулярна і до самої похилої.
Теорема (обернена до теореми про три перпендикуляри). Якщо пряма, проведена на площині через основу похилої, перпендикулярна до похилої, то вона перпендикулярна і до проекції похилої.
Теорема (про паралельні прямі та перпендикулярну площину).
Якщо площина перпендикулярна до однієї з двох паралельних прямих, то вона перпендикулярна і до другої.
Теорема (про паралельні площини та перпендикулярну пряму).
Якщо пряма перпендикулярна до однієї з паралельних площин, то вона перпендикулярна і до другої.
Кутом між площинами , які перетинаються, називається кут між прямими, проведеними в цих площинах зі спільної точки перпендикулярно до лінії їх перетину.
Дві площини називаються перпендикулярними , якщо кут між ними дорівнює 90о.
Теорема (ознака перпендикулярності площин).
Якщо площина проходить через пряму, перпендикулярну до другої площини, то ці площини перпендикулярні.
Теорема (властивість перпендикулярних площин).
Якщо дві площини перпендикулярні, то будь-яка пряма, що лежить в одній з них і перпендикулярна до прямої їх перетину, перпендикулярна до другої площини.
Відстанню між мимобіжними прямими називається довжина їх спільного перпендикуляра.
Якщо пряма l перпендикулярна до площини a , то таке проектування називають ортогональним або прямокутним.
Теорема (про площу ортогональної проекції многокутника).
Площа ортогональної проекції многокутника на площину дорівнює добутку його площі на косинус кута між площиною многокутника і площиною проекції.

(Додаток )
Навчально-методична картка
УРОК 1
Тема. Перпендикулярність прямих у просторі. Ознака перпендикулярності прямої і площини.
Мета: формувати в учнів уміння і навички доведення теорем про перпендикулярність прямих, прямої і площини; сприяти розвитку просторової уяви, продовжувати розвивати навички самостійної роботи; виховувати культуру математичного мовлення.
Обладнання. Саморобні моделі, переносна дошка, стереометричний ящик.
ХІД УРОКУ
I. Організаційний момент.
II. Повідомлення теми, мети уроку.
ПІ. Вивчення нового матеріалу.
Запитання до класу
- Які дві прямі називаються перпендикулярними?
-
Що можна сказати про взаємне розміщення прямих а і b, якщо а1 || а, b1
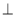 b, а1
b, а1 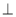 b1?
b1?
- Скільки площин можна провести через дві перпендикулярні прямі?
План доведення теореми
- Ознайомитись з формулюванням теореми (підручник), побудувати в зошиті малюнок до теореми і записати умову і висновок.
-
 Довести що а1
Довести що а1  b1.
b1.
1-й випадок
Якщо прямі а, b, а1, b1 лежать в одній площині, доведення виконується усно за малюнком на кодоплівці.
Дано: а ![]() b, а || а1, b || b1.
b, а || а1, b || b1.
Довести: а1 ![]() b1.
b1.
Доведення
Чотирикутник — паралелограм, у якого один кут прямий, тому протилежний йому кут теж прямий.
Тоді а1 ![]() b1.
b1.
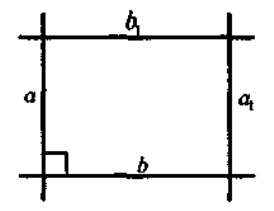
 2-й випадок
2-й випадок
Прямі а, b, а1, b1 не лежать в одній площині. Тоді прямі а і b лежать у деякій площині α, а прямі а1 і b1 — у площині α1.
Учні самостійно доводять теорему, відповідаючи на запитання.
- Чому а || α1, b || α1 і α || α1 ?
-
Що означає: прямі а і а1 паралельні, прямі b
і b1 паралельні? -
Як довести, що чотирикутники СС1А1A,
ВСС1В1 і АА1В1В — паралелограми? -
Рівність яких фігур слід довести, щоб вивести, що а1
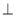 b1 ?
b1 ?
Потім за моделлю один-два учні усно повторюють доведення теореми.
Запитання до класу
-
Чи правильні твердження:
-
якщо пряма а
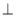 b, b
b, b 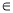 α, то а
α, то а 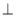 α;
α;
-
якщо пряма а перпендикулярна до b і с, які належать одній площині, і три прямі перетинаються в одній точці, то a
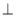 α?
α?
-
якщо пряма а
-
Як розміщені прямі а1 і b1, якщо a1 || а , b1 || b, b
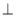 а (а і b перетинаються)?
а (а і b перетинаються)?
-
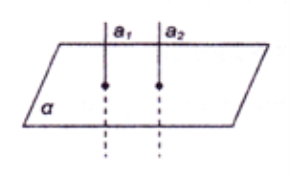
Як розміщені прямі а1, а2 і площина α, якщо а1 || а2, а1
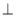 α?
α?
- Який трикутник називається рівнобедреним?
- Що називається медіаною трикутника?
- Яка властивість медіани, проведеної до основи рівнобедреного трикутника?
План доведення теореми .
- Дати означення перпендикулярності прямої і площини.
- Ознайомитись з теоремою, записати в зошит умову теореми і висновок.
- Довести рівність: ∆А1ВС = ∆А2ВС.
- Довести, що ∆А1ХА2 — рівнобедрений.
- Назвати властивість прямої АХ у ∆А1ХА2.
За малюнком на дошці або за моделлю один-два учні повторюють доведення теореми.
IV. Підсумок уроку.
V. Домашнє завдання
Навчально-методична картка
УРОК 2
Тема. Перпендикулярність прямих у просторі. Розв’язування вправ.
Мета: формувати в учнів уміння й навички застосовувати вивчені теореми під час розв'язування задач; розвивати просторову уяву, логічне мислення, виховувати інтерес до математики.
Обладнання. Стереометричний ящик, картки.
ХІД УРОКУ
I. Організаційний момент.
II. Актуалізація опорних знань.
Перевірка домашнього завдання (Задача №348, 354, 361).
- Робота двох сильних учнів біля дошки за картками.
Картка № 1. Дано прямокутну трапецію АВСD: АВ ![]() АВ і АВ
АВ і АВ ![]() ВС. Через вершину В проведено пряму ВЕ, яка не лежить у площині трапеції і перпендикулярна до ВС. Довести, що ВС перпендикулярна до площини АВЕ.
ВС. Через вершину В проведено пряму ВЕ, яка не лежить у площині трапеції і перпендикулярна до ВС. Довести, що ВС перпендикулярна до площини АВЕ.
Картка № 2. Дано рівнобедрений ∆АВС (АВ = ВС), М — середина сторони АС. Через точку D, що не лежить у площині ∆АВС, і точку М проведено пряму МD ![]() МВ. Довести, що ВМ перпендикулярна до площини АВС.
МВ. Довести, що ВМ перпендикулярна до площини АВС.
Запитання до учнів
- Які дві прямі називаються перпендикулярними?
- Сформулювати теорему про перпендикулярність прямих у просторі.
- Яка пряма називається перпендикулярною до площини?
- Сформулювати теорему про перпендикулярність прямої і площини.
- Довести теореми 3.1 і 3.2.
(Учні доводять теореми на аркушах).
III. Розв'язування задач.
Задача 4
|
Дано: ∆АВС, Знайти: ВD, ВС.
|
|
Розв'язання
З ∆ АВС (![]() С = 90°) знайдемо АВ:
С = 90°) знайдемо АВ:![]() ,
, ![]() .
.
DА ![]() пл. ∆ АВС, тому DА
пл. ∆ АВС, тому DА ![]() АВ і DА
АВ і DА ![]() АС.
АС.
З ∆DBA (![]() DAB = 90°) знайдемо ВD:
DAB = 90°) знайдемо ВD: ![]() ,
, ![]() .
.
З ∆ DСА (![]() ВАС = 90°) знайдемо DС:
ВАС = 90°) знайдемо DС: ![]() ,
, ![]() .
.
Відповідь. ![]() ,
, ![]() .
.
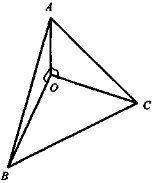
Задача 5. Промені ОА, ОВ, ОС попарно перпендикулярні. Знайти периметр ∆АВС, якщо ОА = ОВ = 3 дм, ОС = 4 дм.
|
Дано: OA OA = ОВ = 3 дм, ОС = 4 дм.
Знайти: Розв'язання
З ∆АВО (
З ∆AСО ( |
|
∆AОС = ∆BОС (прямокутні, АО = ОВ, ОС — спільна), тому ВС = АС,
ВС = 5 дм. Тоді Р= 2АС + АВ = 10 + 3![]() (дм).
(дм).
Відповідь. 10 + ![]() дм.
дм.
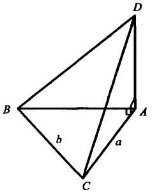
Задача 6. Відрізки АВ, АС, АD попарно перпендикулярні. АВ = а, ВС = b, ВD = с, (с > а, b > а). Знайти довжину відрізка СD.
|
Дано: АВ Знайти: СD. Розв'язання
З ∆ АВС (
З ∆ ВDА (
|
|
З ∆ СDA (![]() САD = 90°) знайдемо СD:
САD = 90°) знайдемо СD:
![]() .
.
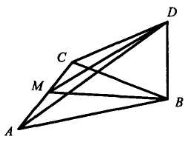
Задача 7. Пряма ВD утворює прямі кути зі сторонами АВ і ВС рівностороннього трикутника АВС, у якому ВМ — висота. Знайти DМ, якщо АС = 2 дм, ВD = 1 дм.
Дано: ∆ АВС - рівносторонній,
![]() DВА =
DВА = ![]() DВС = 90°, ВМ
DВС = 90°, ВМ ![]() AС.
AС.
АС = 2 дм, BD = 1 дм.
Знайти: DМ.
Розв'язання
Якщо BD ![]() AB, ВD
AB, ВD ![]() BС (за умовою), то ВD
BС (за умовою), то ВD ![]() ВМ і
ВМ і ![]() DВМ = 90°.
DВМ = 90°.
AB = BС = AС = 2 дм (за умовою).
З ∆ АВС знайдемо висоту ВМ за формулою: ВМ = ВС ∙ ![]() =
= ![]() (дм).
(дм).
З ∆ DВМ (![]() DВM = 90°) знайдемо DМ:
DВM = 90°) знайдемо DМ:
![]() (дм).
(дм).
Відповідь. DM = 2 дм.
IV. Підсумок уроку.
V. Домашнє завдання.
Навчально-методична картка
УРОК 3
Тема. Побудова перпендикулярних прямої і площини.
Мета: формувати в учнів уміння будувати перпендикулярні пряму і площину в просторі; розвивати просторову уяву; прищеплювати інтерес до предмета.
Обладнання. Картки.
ХІД УРОКУ
I. Організаційний момент.
II. Актуалізація опорних знань.
Перевірка домашнього завдання (Задачі № 354, 366, 370* (стор.113).
- Робота двох учнів біля дошки за картками.
Картка № 1. А, В, С — точки на попарно перпендикулярних променях ОА, ОВ, ОС. Знайти кути трикутника АВС, якщо ОА = ОВ = ОС.
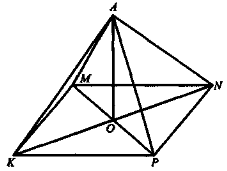
Картка № 2. Точки К i М — середини ребер АВ і СD правильного тетраедра АВСD. Довести, що КМ ![]() АВ і КМ
АВ і КМ ![]() СD Знайти КМ, якщо АВ = а.
СD Знайти КМ, якщо АВ = а.
- За моделями повторити доведення теорем 3.1 і 3.2.
- Розв'язування задачі з коментуванням.
Задача
|
Дано: ∆АВС ( АС = а, ВС = b, АD = с. Знайти: ВD, СD. Розв'язання
Якщо АD
З ∆ DСА (
З ∆АВС ( |
|
З ∆ DВА (![]() DАВ = 90°) знайдемо ВD:
DАВ = 90°) знайдемо ВD: ![]() .
.
Відповідь. ![]() ,
,![]() .
.
III. Вивчення нового матеріалу.
-
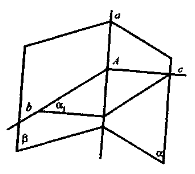 Колективне розв'язування задачі .
Колективне розв'язування задачі .
Дано: Пряма а, А ![]() а .
а .
Побудувати: α ![]() а .
а .
Розв'язання
Проведемо через пряму а і точку А дві площини: α і β. У площині α проведемо с ![]() а, у площині β b
а, у площині β b ![]() а. Через прямі b і с проведемо площину α1, α1
а. Через прямі b і с проведемо площину α1, α1 ![]() а.
а.
Доведемо, що площина α1 — єдина.
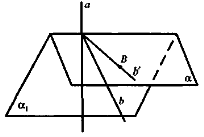 Припустимо, що існує α' і α'
Припустимо, що існує α' і α' ![]() а. Проведемо через пряму а і точку В площину, яка перетинає α1 і α' по прямих b і b'.
а. Проведемо через пряму а і точку В площину, яка перетинає α1 і α' по прямих b і b'.
b' ![]() а , b
а , b ![]() а, що неможливо. Отже, площина α1 — єдина.
а, що неможливо. Отже, площина α1 — єдина.
- Закріплення матеріалу.
Учні за підручником розв'язують задачу №369 § 9.
Після цього один учень за готовим малюнком на дошці записує її розв'язання.
IV. Підсумок уроку.
V. Домашнє завдання.
Навчально-методична картка
УРОК 4
Тема. Властивості прямої і площини, перпендикулярних між собою.
Мета: довести теореми та застосовувати їх до розв'язування задач, розвивати вміння учнів аналізувати, робити висновки, виховувати ціннісне ставлення особистості до праці
ХІД УРОКУ
I. Організаційний момент.
II. Актуалізація опорних знань.
- Перевірка домашнього завдання.
- Відповіді на запитання.
- Які прямі називаються перпендикулярними?
- Сформулювати ознаку перпендикулярності прямої і площини.
- Усно за готовим малюнком розв'язати задачу 1 (стор 109).
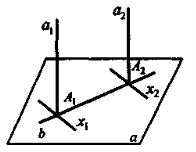
III. Вивчення нового матеріалу.
Дано: a1 || a2, α || а1.
Довести: α ![]() a2.
a2.
Доведення
Прямі a1 і а2 перетинають площину α: а2 ![]() α = А2, а1
α = А2, а1 ![]() α = А1.
α = А1.
Проведемо через точку А2 довільну пряму х2, а через точку A1 пряму х1 || х2.
Пряма a1 ![]() α, тому a1
α, тому a1 ![]() x1; a1 || а2, х1 || х2, тому а2
x1; a1 || а2, х1 || х2, тому а2 ![]() х2, що означає а2
х2, що означає а2 ![]() α.
α.
Теорему 3.4 учні опрацьовують самостійно. Після цього 1—2 учні біля дошки за готовим малюнком відтворюють її доведення.
IV. Розв'язування задач.
Задача 1
|
Дано: АС СD = 2,4 м. Знайти: АВ. Розв'язання
Якщо АС
∆ ABK - прямокутний ( |
|
AK = AС – СК, АК = 1 м. ![]() ,
, ![]() (м).
(м).
Відповідь. 2,6 м.
Задача 2
|
Дано: ∆ DВС — рівносторонній, СD = а, АВ = АС = АD = а. Знайти: АО. Розв'язання
Якщо точка А рівновіддалена від вершин трикутника, то пряма ОА |
|
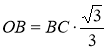 ,
, 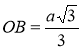 .
.
З ∆ АВО (![]() АОВ = 90°) знайдемо АО.
АОВ = 90°) знайдемо АО. ![]() ,
, 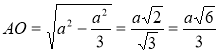 .
.
Відповідь. ![]() .
.
Задача 3
|
Дано: МNРК – квадрат, NM = b, АК = АМ =AN = AP = a. Знайти: АО. Розв'язання
Якщо точка А рівновіддалена від вершин квадрата, то АО |
|
З ∆ KNP (![]() КРN = 90°) знайдемо KN: КN =
КРN = 90°) знайдемо KN: КN = ![]() .
.
ON = ![]() КN, ON =
КN, ON = ![]() .
.
З ∆ AON (![]() AON = 90°) знайдемо ОА:
AON = 90°) знайдемо ОА:
![]() ,
, 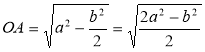 .
.
Відповідь. 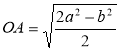 .
.
V. Підсумок уроку.
VI. Домашнє завдання.
Навчально-методична картка
УРОК 5
Тема. Властивості перпендикулярних прямої і площини. Розв'язування задач.
Мета: формувати навички застосування вивчених теорем, розвивати навички самостійної розумової діяльності, виховувати культури математичного мислення.
Обладнання. Стереометричний ящик, картки.
ХІД УРОКУ
І. Організаційний момент.
II. Актуалізація опорних знань.
- Сформулювати і довести теорему про властивість площини, перпендикулярної до однієї з двох паралельних прямих.
- Довести теорему про властивість двох прямих, перпендикулярних до однієї площини.
- Робота трьох учнів за картками (за партами).
Картка № 1. Точка М однаково віддалена від усіх вершин правильного трикутника АВС зі стороною 8![]() см і віддалена від його площини на 6 см. Знайти відстань від точки M до вершин трикутника.
см і віддалена від його площини на 6 см. Знайти відстань від точки M до вершин трикутника.
Картка № 2. Точка рівновіддалена від усіх вершин прямокутника і знаходиться на відстані 8 см від його площини. Знайти відстань від цієї точки до вершин прямокутника, якщо його менша сторона дорівнює 8 см, а діагональ утворює з більшою стороною кут 30°.
Картка № 3. Точка М віддалена від кожної вершини трикутника АВС на 10 м. У ∆ АВС: АВ = АС = 12 м, висота АЕ = 9 м. Знайти відстань від точки М до площини трикутника АВС.
III. Розв'язування задач.
Задача (колективне розв'язування біля дошки з коментуванням). У ∆ АВС кут А дорівнює 45°, ВС = 12 см. Точка М, віддалена від площини трикутника на 6 см, знаходиться на однаковій відстані від усіх вершин трикутника. Знайти довжини МА, МВ і МС.
|
Дано: ∆АВС,
МО Знайти: МА, МВ, МС. Розв'язання Якщо МА = МВ = МС, то О — центр кола, описаного навколо ∆АВС, ОВ — радіус описаного кола.
|
|
R = 6![]() см.
см.
Якщо МО ![]() (АВС), то MO
(АВС), то MO ![]() ОВ.
ОВ.
З ∆ МОВ (![]() МОВ = 90°) знайдемо МВ:
МОВ = 90°) знайдемо МВ: ![]() ,
, ![]()
Відповідь. МА = МВ = МС = ![]() см.
см.
IV. Підсумок уроку.
V. Домашнє завдання.
Задача
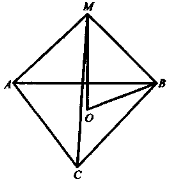
|
Дано: АВСD — квадрат, ВМ
Довести: АО Доведення
1) ВС
Отже, ВС
АD || ВС, тому за теоремою 3.3 АD |
|
2) АВ ![]() ВМ і АВ
ВМ і АВ ![]() ВС.
ВС.
Отже, АВ ![]() (ВСМ).
(ВСМ).
СD || АВ, тому СD ![]() (BСM).
(BСM).
Навчально-методична картка
УРОК 6
Тема. Перпендикуляр і похила. Кут між прямою і площиною.
Мета: формувати знання учнів про перпендикуляр і похилу, кут між похилою та площиною; показати взаємозв'язок між планіметрією та стереометрією. Виховувати моральні якості.
Обладнання. Таблиця, екліметр, кодоскоп, відкидна дошка з планом уроку.
ХІД УРОКУ
I. Організаційний момент.
II. Актуалізація опорних знань.
Фронтальне опитування
- Що називається перпендикуляром до даної прямої?
- Як називається точка перетину перпендикуляра і прямої?
- Які прилади використовуються для побудови перпендикуляра?
-
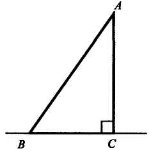 Скільки перпендикулярів можна провести з даної точки до даної прямої?
Скільки перпендикулярів можна провести з даної точки до даної прямої?
- Як називаються відрізки, відмінні від перпендикуляра АС, на малюнку?
- 3 якої теореми випливають властивості похилої?
III. Вивчення нового матеріалу.
- Робота з підручником.
План
- Що називається перпендикуляром до площини?
- Що називається похилою до площини?
- Що таке основа похилої і основа перпендикуляра?
- Що таке проекція похилої?
- Що називається відстанню від точки до площини?
(За цим планом один учень будує малюнок і відповідає на запитання).
Запитання до класу
- Які ви можете назвати випадки взаємного розміщення прямої і площини у просторі?
- Назвіть ознаки паралельності прямої і площини, перпендикулярності прямої і площини.
- Пояснення вчителя.
Якщо пряма паралельна площині або належить їй, то кут між ними дорівнює 0°.
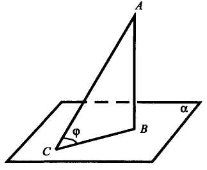 Якщо пряма перпендикулярна до площини, то кут між прямою і площиною дорівнює 90°.
Якщо пряма перпендикулярна до площини, то кут між прямою і площиною дорівнює 90°.
Кут між прямою і площиною — це кут між прямою та її проекцією на площину. Отже, 0° ≤ φ ≤ 90°.
Запитання до класу
-
Наведіть життєвий приклад перпендикуляра
до площини. - Наведіть приклад похилої до площини з навколишнього середовища.
- Якими приладами вимірюють кут між похилою і горизонтальною площиною геодезисти, будівельники доріг?
IV. Розв'язування задач.
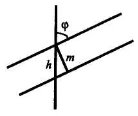 Задача 1. Знайти товщину т вугільного пласта, якщо вертикальна свердловина нахилена до нього під кутом φ = 72° і проходить по вугіллю відстань h = 2,50 м.
Задача 1. Знайти товщину т вугільного пласта, якщо вертикальна свердловина нахилена до нього під кутом φ = 72° і проходить по вугіллю відстань h = 2,50 м.
Дано: h = 2,50 м, φ = 72°.
Знайти: т.
Розв'язання
т = h sіn φ, т = 2,50 ∙ sіn 72° ![]() 2,50 ∙ 0,90 = 2,375
2,50 ∙ 0,90 = 2,375 ![]() 2,4 (м).
2,4 (м).
Відповідь. т ![]() 2,4 м.
2,4 м.
Задача 2 (колективне розв'язування біля дошки з коментуванням). З точки М до площини α проведено похилі АМ і МВ та перпендикуляр МС, який дорівнює а. Кут між кожною похилою та перпендикуляром 45°. Знайти:
1) площу ∆АВС, якщо проекції похилих перпендикулярні;
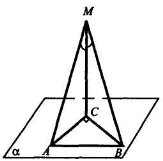 2) кут між похилими.
2) кут між похилими.
Дано: АМ і МВ — похилі, МС ![]() α, МС = а,
α, МС = а,
![]() АМС =
АМС = ![]() ВМС = 45°; АС
ВМС = 45°; АС ![]() ВС.
ВС.
Знайти: SАВС, ![]() АМВ.
АМВ.
Розв'язання
Якщо МС ![]() α, то МС
α, то МС ![]() АС і МС
АС і МС ![]() ВС.
ВС.
∆АМС = ∆ВМС (прямокутні, ![]() АМС =
АМС = ![]() ВМС). Тоді МА = МВ, АС = ВС,
ВМС). Тоді МА = МВ, АС = ВС, ![]() МАС =
МАС = ![]() МВС = 45°, АС = СМ, АС = а, ВС = а.
МВС = 45°, АС = СМ, АС = а, ВС = а.
З ∆АМС: ![]() . SABC =
. SABC = ![]() AC ∙ВС,
AC ∙ВС, 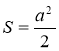 .
.
З ∆АВС: АВ = ![]() , АМ = МВ = АВ =
, АМ = МВ = АВ = ![]() .
.
Отже, ∆АМВ — рівносторонній, тоді ![]() АМВ = 60°.
АМВ = 60°.
Відповідь. ![]() ,
, ![]() АМВ = 60°.
АМВ = 60°.
V. Підсумок уроку.
VI. Домашнє завдання.
Задача. На якій глибині знаходиться станція метро, якщо її ескалатор має довжину 35 м і нахилений до площини горизонту під кутом 42°?
Навчально-методична картка
УРОК 7
Тема. Перпендикуляр і похила. Розв'язування задач.
Мета: формувати в учнів уміння й навички застосовувати означення перпендикуляра і похилої до розв'язування задач, розвивати просторову уяву. Виховувати культуру математичного запису.
Обладнання. Стереометричний ящик, кольорова крейда, мультимедійна дошка.
ХІД УРОКУ
I. Організаційний момент.
II. Актуалізація опорних знань.
- Перевірка домашнього завдання.
- Фронтальне опитування.
- Що називається перпендикуляром, опущеним з даної точки на площину?
- Що таке відстань від даної точки до площини?
- Що називається похилою, проведеною з даної точки до площини?
- Що таке проекція похилої на площину?
- Що називається кутом між прямою і площиною?
- Чому дорівнює кут між перпендикулярними прямою і площиною? паралельними прямою і площиною?
- Що називається відстанню від прямої до паралельної їй площини?
- Що називається відстанню між паралельними площинами?
-
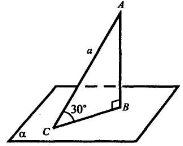 Усне розв'язування задач з використанням мультимедійної дошки.
Усне розв'язування задач з використанням мультимедійної дошки.
Задача 1. Довжина похилої 10 см, довжина перпендикуляра 8 см. Знайти довжину проекції похилої.
Задача 2. Довжина похилої а, ![]() С = 30°. Знайти довжину перпендикуляра.
С = 30°. Знайти довжину перпендикуляра.
Задача 3. Довжина перпендикуляра b, ![]() А = 45°. Знайти довжину похилої.
А = 45°. Знайти довжину похилої.
III. Розв'язування задач.
Задача № 387 (§ 10 підручника).
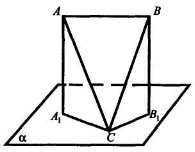 Дано: ∆АВС,
Дано: ∆АВС, ![]() АСВ = 90°, АВ || α, АА1
АСВ = 90°, АВ || α, АА1 ![]() α, ВВ1
α, ВВ1 ![]() α, АА1 = ВВ1 = 1 м,
α, АА1 = ВВ1 = 1 м,
А1С = 3 м, СВ1 = 5 м.
Знайти: АВ.
Розв'язання
АA1 ![]() α, тоді АA1
α, тоді АA1 ![]() СА1 і
СА1 і ![]() АА1С = 90°.
АА1С = 90°.
З ∆ АА1С знайдемо AС: ![]() ,
, ![]() (м).
(м).
BB1 ![]() α, тоді ВB1
α, тоді ВB1 ![]() СB1,
СB1, ![]() BB1С = 90°.
BB1С = 90°.
З ∆ BB1С знайдемо BC: ![]() ,
, ![]() (м).
(м).
З ∆АВС знайдемо АB: ![]() ,
, ![]() (м).
(м).
Відповідь. АВ = 6 м.
Задача
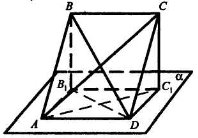 Дано: АВСD — ромб, BC || α, BВ1
Дано: АВСD — ромб, BC || α, BВ1 ![]() α, СС1
α, СС1 ![]() α,
α,
ВВ1 = СС1 = 4 м, В1D = 2 м, AС1 = 8 м.
Знайти: АВ1 = DС1, B1C1.
Розв'язання
З ∆BB1D (![]() BB1D = 90°) знайдемо BD:
BB1D = 90°) знайдемо BD:
![]() ,
, ![]() (м).
(м).
З ∆AСС1 (![]() AС1C = 90°) знайдемо АС:
AС1C = 90°) знайдемо АС:
![]() ,
, ![]() (м).
(м).
У ромбі АВСD: АС2 + BD2 = 4АВ2, (![]() )2 + (
)2 + (![]() )2 = 4АB2, 4АB2 = 100, АВ2 = 25 , AB = 5 м.
)2 = 4АB2, 4АB2 = 100, АВ2 = 25 , AB = 5 м.
З ∆ DC1C знайдемо DС1: ![]() ,
, ![]() (м).
(м).
 Відповідь. АВ1 = DС1 = 3 м, B1C1 = 5 м.
Відповідь. АВ1 = DС1 = 3 м, B1C1 = 5 м.
Задача № 389 (§ 10 підручника).
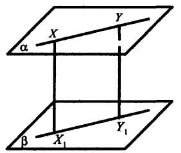
Дано: α || β, ХХ1 ![]() β, YY1
β, YY1 ![]() β.
β.
Довести: ХХ1 = YY1.
Доведення
Нехай X і Y дві довільні точки площини α. Їх відстані до площини β — це XX1 і YY1 , де ХХ1 ![]() β і YY1
β і YY1 ![]() β.
β.
ХХ1 || YY1 (за теоремою 3.4).
(ХХ1Y) ![]() α = ХY, (ХХ1Y)
α = ХY, (ХХ1Y) ![]() β = Х1Y1. ХY || X1Y1.
β = Х1Y1. ХY || X1Y1.
Отже, XYY1X1 — паралелограм і ХХ1 = YY1.
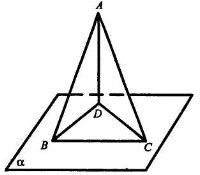 Задача № 395 (§ 10 підручника).
Задача № 395 (§ 10 підручника).
Дано: АD ![]() α, АB і AC – похилі,
α, АB і AC – похилі,
АВ = АС = 2 м, ![]() ВАС = 60°, ВD
ВАС = 60°, ВD ![]() DС.
DС.
Знайти: АD.
Розв'язання
∆ ВАС — рівнобедрений, оскільки АВ = АС, тоді ![]() ABC =
ABC = ![]() ACB = (180° – 60°) : 2 = 60°.
ACB = (180° – 60°) : 2 = 60°.
Отже, АВ = АС = BС = 2 м. Якщо похилі рівні, то їх проекції також рівні: DВ = DС, тому прямокутний трикутник ВDС — рівнобедрений.
З ∆ ВDС знайдемо BD = DС: ВС2 = 2ВD2, ВD2 = 2, ВD = DС = ![]() (м).
(м).
АD ![]() α, тому АD
α, тому АD ![]() DВ, АD
DВ, АD ![]() DC.
DC.
З ∆ADB знайдемо АD: ![]() (м).
(м).
Відповідь. АD = ![]() м.
м.
IV. Підсумок уроку.
V. Домашнє завдання.
Навчально-методична картка
УРОК 8
Тема. Розв'язування задач. Самостійна робота.
Мета: формувати в учнів навички і вміння обчислювати довжини перпендикуляра і похилої до площини, знаходити кут між похилою і площиною, розвивати навички самостійної діяльності на уроці. Виховувати самостійність.
Обладнання. Ноутбук.
ХІД УРОКУ
I. Організаційний момент.
II. Актуалізація опорних знань.
- Перевірка домашнього завдання.
III. Самостійна робота.
1-й варіант
- Пряма АВ утворює з площиною α кут 60°. Знайти довжину проекції похилої АВ на площину α, якщо АВ = 48 см.
- Сторона квадрата АВСD дорівнює 6 см, точка М знаходиться на відстані 6 см від кожної з його вершин. Знайти кут між прямою МА і площиною квадрата.
- До площини квадрата АВСD проведено перпендикуляр DМ довжиною 12 см. Сторона квадрата 5 см. Знайти довжини похилих МА, МВ, МС.
2-й варіант
- Довжина похилої АВ дорівнює 50 см, точка А віддалена від площини на 25 см. Знайти кут між похилою і площиною.
-
Сторона рівностороннього трикутника дорівнює 3a, точка М віддалена від кожної з його вершин на 2а. Під якими кутами нахилені прямі МА,
МВ, МС до площини цього трикутника? -
Точка М віддалена від кожної вершини квадранта на 13 дм. Знайти відстань від точки M до площини квадрата, якщо його сторона дорівнює 6
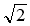 дм.
дм.
IV. Підсумок уроку.
V. Домашнє завдання.
3-й варіант
- Довжини перпендикуляра і проекції похилої дорівнюють по 15 см. Знайти кут між похилою і площиною.
-
Точка М знаходиться на відстані 10 см від вершини рівностороннього трикутника зі стороною 6
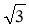 см. Знайти відстань від точки М до площини трикутника.
см. Знайти відстань від точки М до площини трикутника.
-
Через точку О перетину діагоналей квадрата зі стороною 4 см проведено перпендикуляр ОМ = 2
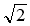 см до площини квадрата. Знайти відстань від точки M до вершин квадрата.
см до площини квадрата. Знайти відстань від точки M до вершин квадрата.
Навчально-методична картка
УРОК 9
Тема. Теорема про три перпендикуляри.
Мета: сформулювати і довести теорему про три перпендикуляри, показати її практичне застосування, сприяти розвитку просторової уяви, самостійного мислення; прищеплювати інтерес до математики.
Обладнання. Модель до теореми про три перпендикуляри, стереометричний ящик.
ХІД УРОКУ
I. Організаційний момент.
II. Актуалізація опорних знань учнів.
Фронтальне опитування
- Що називається перпендикуляром, опущеним з даної точки на площину?
- Що називається похилою?
- Що називається проекцією похилої?
- Назвіть залежність між довжинами:
а) перпендикуляра і похилої,
б) рівних похилих,
в) різних похилих.
III. Вивчення нового матеріалу.
Доведення теореми можна здійснювати за малюнком на дошці або за моделлю.
Дано: AB ![]() α, AC – похила, ВС – проекція похилої АС на площині α.
α, AC – похила, ВС – проекція похилої АС на площині α.
-
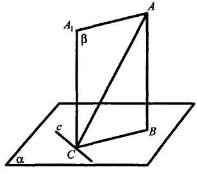 с
с 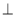 ВС,
ВС,
-
с
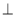 АС.
АС.
Довести:
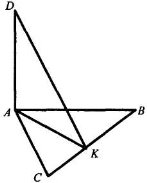
-
с
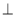 ВС,
ВС,
-
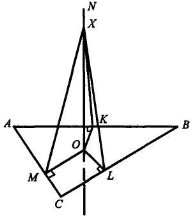
с
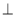 АС.
АС.
Доведення
Проведемо пряму СА1 || АВ, тоді СА ![]() α. Проведемо площину β через прямі АВ і А1С. Пряма с
α. Проведемо площину β через прямі АВ і А1С. Пряма с ![]() СА1 і с
СА1 і с ![]() СВ , тому пряма с
СВ , тому пряма с ![]() β, а отже, с
β, а отже, с ![]() АС.
АС.
Якщо пряма с ![]() АС і с
АС і с ![]() СА1, то с
СА1, то с ![]() β. ВС лежить у площині β, тому с
β. ВС лежить у площині β, тому с ![]() ВС. Теорему доведено.
ВС. Теорему доведено.
IV. Розв'язування задач.
 Учні виконують малюнки самостійно на окремому аркуші, а потім перевіряють правильність побудови за готовим малюнком, що проектується з кодоскопа.
Учні виконують малюнки самостійно на окремому аркуші, а потім перевіряють правильність побудови за готовим малюнком, що проектується з кодоскопа.
Задача 1. З вершини А рівнобедреного ∆ АВС проведено перпендикуляр АО до його площини. Побудувати відрізок, який визначає відстань від точки D до сторони ВС.
Розв'язання
∆АВС — рівнобедрений (АС = АВ), АD ![]() (АВС).
(АВС).
У ∆АВС проведемо медіану АК до основи ВС, АК ![]() ВС. Сполучимо точки D і К, АD
ВС. Сполучимо точки D і К, АD ![]() (АВС), АК — проекція похилої ОК на площину АВС. ВС
(АВС), АК — проекція похилої ОК на площину АВС. ВС ![]() АК, то ВС
АК, то ВС ![]() ОК (за теоремою про три перпендикуляри). Отже, DК — шукана відстань.
ОК (за теоремою про три перпендикуляри). Отже, DК — шукана відстань.
Відповідь. Шукана відстань ОК.
 Задача 2. Знайти DК з попередньої задачі, якщо основа ВС рівнобедреного трикутника АВС дорівнює 12 см, бічна сторона 10 см, довжина перпендикуляра АО дорівнює 6 см.
Задача 2. Знайти DК з попередньої задачі, якщо основа ВС рівнобедреного трикутника АВС дорівнює 12 см, бічна сторона 10 см, довжина перпендикуляра АО дорівнює 6 см.
Відповідь. DК = 10 см.
Задача
Дано: ∆ АВС, точка О — центр вписаного кола, ОN ![]() (АВС).
(АВС).
Довести: кожна точка ON рівновіддалена від сторін ∆ АВС.
Доведення
Нехай X — довільна точка прямої ОN і X ≠ O.
Опустимо з точки О перпендикуляри на сторони ∆АВС: ОК ![]() АВ, ОL
АВ, ОL ![]() СВ, ОМ
СВ, ОМ ![]() АС. ОК = ОL = ОМ (за умовою). Сполучимо ці точки з точкою X. ХК — похила, ОК — її проекція. За теоремою про три перпендикуляри ХК
АС. ОК = ОL = ОМ (за умовою). Сполучимо ці точки з точкою X. ХК — похила, ОК — її проекція. За теоремою про три перпендикуляри ХК ![]() АВ. Аналогічно доводимо, що ХL
АВ. Аналогічно доводимо, що ХL ![]() СВ і ХМ
СВ і ХМ ![]() АС.
АС.
∆ ОХК = ∆ ОХL = ∆ ОХМ (за двома катетами).
Отже, ХК = ХL = ХМ.
V. Підсумок уроку.
VI. Домашнє завдання.
Бібліографія
- Закон України «Про освіту», 2018р.
- Антонов Г. Дистанційне навчання: мода чи потреба? // Освіта України. – 4 квітня (№25). – с. 10
- Биков В. Ю., Кухаренко В. М., Сиротинко Н. Г., Рибалко О. В. Технологія розробки дистанційного курсу: Навчальний посібник / За ред. В. Ю. Бикова та В. М. Кухаренка. – К.: Міленіум, 2008. – 324 с.
- Варзар Т. Дстанційна освіта в сучасній освітній діяльності //Українознавство. – 2005. –№ 1. – С. 116–119.
- Дистанційне навчання: Тренінг з організації дистанц. навчання на платформі WebСТ. – Режим доступу: httр://www. users. kharkіv. com. - Заголовок з екрана.
- Сисоєва С. О. Методологічні проблеми дистанційного навчання // Вісн. Акад. дистанц. освіти. – 2004. –№ 2. – С. 21– 28.
- Система дистанційної освіти та перевірки знань: Сервер інформ. технологій каф. Фундамент. дисциплін АПБУ. – Режим доступу: httр://www. fdapbu. narod. rи. – Заголовок з екрана.
- Створення дидактичних матеріалів з дистанційної форми навчання: Інформ. - метод. зб. / П. М. Таланчук, А. Г. Шевцов, В. Т. Бажан, В. М. Ген-ба. – К.: Ун-т "Україна", 2001. – 48 с.
- Шукевич Б. Шляхи поповнення терміносистеми з дистанційного навчання// Українська термінологія і сучасність: Зб. наук. праць. Вип VІ / Відп. ред. Л. О. Симоненко. – Київ.: КНЕУ, 2005. – С. 437 – 440.
1


про публікацію авторської розробки
Додати розробку