Міністерство освіти і науки України

Державний навчальний заклад

«Полтавське вище міжрегіональне професійне училище»

 

 36007 м. Полтава 

                                                       вул. М.Бірюзова, 64-А тел. (0532)67-70-98

                                                                                                      poltava.vmpu@ukr.net

 

Задачі професійного змісту

на уроках математики

          Заєць Валентина Михайлівна викладач математики і фізики   

Полтава

 2017

 

В сучасних умовах, одна із задач навчального закладу – забезпечення реального зв’язку з життям. На уроках математики цю проблему допомагає вирішити професійна спрямованість навчання. Викладач повинен навчити учнів використовувати знання під час вивчення, як самої математики, так й інших навчальних дисциплін, а в подальшому творчо застосовувати ці знання у своїй роботі.

Даний посібник містить рекомендації, задачі із розв’язками розраховані на зв'язок теорії з практикою та завдання, які можуть бути використані викладачами математики професійно-технічних навчальних закладів при підготовці до занять, а також учнями при виконанні завдань до захисту дипломних робіт. Задачі, підібрані із урахуванням особливостей підготовки робітників різних спеціальностей і дають можливість наглядно показати використання математичних знань в житті та обраній професії.

 

 

Розглянуто та затверджено  на засіданні методичної комісії                                      Протокол № 3 від «17»жовтня 2017року

 

 

 

 

 

 

Заєць В.М.

Задачі професійного змісту на уроках математики.

Посібник для викладачів. Полтава, 2017 34 с.

Зміст

1.   Професійна спрямованість вивчення математики

2.   Використання математичних розрахунків при підготовці до захисту дипломних робіт

3.   Задачі професійного змісту з геометрії

4.   Задачі професійного змісту з алгебри

5.   Задачі з використанням регіонального компоненту

6.   Література

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

«Не в кількості знань полягає освіта, а в                  повному розумінні й майстерному застосуванні в житті

всього того,  що знаєш»

Дістеверг

Професійна спрямованість вивчення математики – це засіб формування ключових компетентностей  майбутніх робітників. Глибокі якісні зміни на виробництві в цілому і в окремих його галузях та в структурі виробничих сил, приводять до зміни характеру праці кваліфікованого робітника та складу його професії. Зникає потреба в працівниках однієї спеціальності, з'являється необхідність у працівниках іншої спеціальності, викликана новими технологіями на виробництві та новою технікою. Тому робітнику високої кваліфікації потрібні знання, уміння і навики, які дозволяють за короткий час освоїти нову техніку і нові технологічні процеси.

Важливою умовою підвищення якості підготовки робітників в училищах є взаємозв'язок між предметами загальноосвітнього, загальнотехнічного і спеціального циклів. В зв'язку з підвищенням вимог сучасного виробництва до загальноосвітньої підготовки робітників, особливу увагу треба приділяти вивченню математики. Пояснюється це тим , що значно зросла роль математичних методів і теорій в інших науках. Можна стверджувати , що в сучасних умовах не існує науки, яка б могла обійтися без математичних методів, без застосування швидкодіючих електронно-обчислювальних машин.

Перед вивченням математики ставляться такі практичні завдання:

а) Вміння застосувати математичні знання для розв'язування

важливих практичних задач;

                                      б) Вміння          користуватися         математичними         методами,

інструментами і моделями;

в) Вміння самостійно здобувати знання.

Ці задачі обумовлені сучасним рівнем розвитку техніки, а також динамікою розвитку соціально-економічних факторів.

 Для підготовки кваліфікованих робітників по спеціальності електромонтажник велике значення має знання учнями основних законів електротехніки, будови і принципу дії електровимірювальних приладів, трансформаторів, основних даних із промислової електроніки. Для досягнення цієї мети учням необхідно розуміти фізичний зміст електричних і магнітних явищ та їх взаємозв'язок в кількісному співвідношенні, оволодіти необхідним математичним апаратом для розрахунків характеристик пристроїв і знаходження їх параметрів.

Наприклад, задача з електротехніки, яка розв'язується математичним методом ( система рівнянь).

Задача 1. При збільшенні довжини провідника на 100 м опір його зріс в 3 рази. Знайти попередню довжину провідника .

Для розв'язання задачі необхідно скористатися виразом для

l

знаходження опору: ^{R }S

 Позначимо у = R, x = L,  і одержимо таку систему рівняннь:

                                   yS x;

                                             ^                 

3y (x100).

                                         S

Поділимо почленно друге рівняння на перше і одержимо:

3  xx100  x 50 .м

                           

Можна розв'язати простіше. Так як довжина провідника і опір прямо пропорційні, то збільшення довжини провідника на 100 м відповідає її збільшенню в 3 рази, тобто:

 х + 100 = Зх  =>  х =50 (м)

При викладанні математики треба виділити ті знання учнів професійно-технічного циклу, на які можна опиратися при формуванні нових математичних понять. Так, при вивченні тем геометрії "Паралельна проекція фігури", "Властивості паралельного проектування",  "Зображення фігур в стереометрії" - успішно реалізуються знання учнів з креслення: "Основні поняття про аксонометричні проекції" , "Правила виконання технічних рисунків", "Побудова аксонометричних проекцій ".

При формуванні понять важливе значення має їх узгодження.

Наприклад, майбутні робітники говорять:

•        _МУЛЯРИ: бічна грань многогранника - поперечик, ложок; основа многогранника – постіль;

•        _{СЛЮСАРІ}: висота конуса - довжина конуса; тангенс половини кута при вершині конуса – нахил

При поясненні теми "Паралельність в просторі", в групі машиністів автомобільного крану можна запропонувати такі завдання : в конструкції автомобільного крану навести приклади паралельних прямих, мимобіжних, прямих паралельних площині, паралельних площин.

 Викладач математики училища повинен проводити роботу з учнями з метою орієнтації їх одержаних знаннях на уроках математики, які потрібні для професіональних навичок. Відомо, що така форма навчальної роботи, як складання і розв'язування задач, підказаних проблемами будівництва, викликає інтерес учнів до їх розв'язання. Задачі, які відображають особливості знайомих учням професій, доцільно складати із врахуванням місцевих умов, поступово залучаючи до цієї справи самих учнів. Цікаві дані для складання задач дають екскурсії до майстерень та на будівельні обє'кти, довідки і публікації із періодичної преси. Ось перелік деяких задач, складених із урахуванням особливостей майбутніх професій :

СЛЮСАР – САНТЕХНІК,  ГАЗОЗВАРНИК 

 Задача. При прокладанні труб для парового отоплення один слюсар - газопровідник установив 22 трійники і виконав норму на 155% . Скільки таких же трійників установить другий слюсар за цей же час, якщо у нього норма виробітку на 7 % більше ніж у першого?

МОНТАЖНИК ЗАЛІЗОБЕТОННИХ ВИРОБІВ 

 Задача. Скільки панелей установить за зміну бригада монтажників із чотирьох чоловік, якщо одному монтажнику на установку однієї панелі за нормою відводиться 2,9 години ?

СТОЛЯР БУДІВЕЛЬНИЙ, ПАРКЕТНИК 

 Задача1. Яка кількість дощок необхідна для покриття підлоги майстерні розміром 16 х 5м, якщо довжина дошки 5,1 м , а ширина 30см?

Задача2. При виготовленні короба дверей розміром 210 х 90см використовують брус із перерізом 10 х 5см. Розмір четверні 4 х 1см який % пиломатеріалу піде у відходи ?

МАШИНІСТ ОДНОКІВШОВОГО ЕКСКАВАТОРА.

 Задача. 3а який час екскаватор, що має потужність      150 м³ /год  викопає котлован під будинок, довжиною 120 м, шириною 12м, глибиною 2,5 м ?

СЛЮСАР З РЕМОНТУ АВТОМОБІЛІВ

 Задача. Стальна болванка, довжина якої 10см, а в перерізі квадрат із стороною 60 см виготовляється з відхиленням по стороні квадрата ±1,0 см. Визначити відхилення заготовки у вазі ( густина сталі = 8г/см³ ).

В курсі геометрії учні знайомляться з формами геометричних тіл, формулами для обчислення їх площ поверхні та об'ємів. Часто учні почувають себе зовсім безпорадними при розв'язуванні задач, де геометричні факти не головні, а тільки допоміжні для відповіді на чисто виробниче запитання. Виникають труднощі також при розв'язуванні задач на комбінації геометричних тіл, або такі в яких елементам геометричних фігур і самим фігурам даються технічні назви. Підкреслити треба важливість їх на виробництві в столярній, слюсарній, мулярній справі. 

Задача №1. Паровий котел має довжину 8000 мм і зовнішній діаметр 4000 мм. Яку кількість листів сталі марки Ст. З КТ необхідно для його виготовлення, якщо відомо, що лист сталі такої марки має розміри 6 х 1,5м ? В середині котла проходять чотири жарові труби діаметром  400мм. Обчислити їх загальний обє'м.

Задача №2. Воронка має форму зрізаного конуса, у якого діаметри основи 600мм і 300мм, а висота 500мм. Скільки жерсті піде на її виготовлення, якщо на припуск додають 5% площі поверхні воронки.

В харчовій, хімічній промисловості у великих масштабах використовують металеві посудини, що мають форму прямокутного паралелепіпеда (така форма дозволяє раціонально використовувати виробничі і складські приміщення ). З метою економії при виготовленні посуду заданного об'єму витрати металу, а також емалей, красок, лаку, якими його покривають повинен бути найменшим. Отже виникає така задача:

 Які повинні бути розміри прямокутної посудини данного обє'му V із заданим значенням k, щоб витрати металу на виготовлення були найменшими ?

                    Розв'язання.

Якщо витрати металу на шви не враховувати, а товщину стінок,  дна і кришки вважати однаковою, то за параметр, що визначає витрати металу на виготовлення посуду, можна взяти площу S -  його  поверхні. Нехай розміри посудини x, y, z і взявши z/y = k, одержимо

                      S ay  

2 by ,деa 2k ,  b  2kk1V .

Легко показати, що функція S має найменше значення при b

                      ^{y y }0    ³ 2a і розв'язання задачі подається формулами:  

x0  y zV  3 (k4kV1), y0  3 (k2k1)2V ,z0  3 k k( 21)V .    

0 0

Якщо врахувати, що такий посуд різного об'єму випускається у великій кількості, очевидно, що відхилення від оптимальних розмірів

викличе значні втрати матеріалу.                                

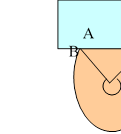
В системах зрошення та каналізаційних мережах і деяких інших спорудах часто використовуються пружні труби, що працюють на частковому заповненні перерізу. На вході такої труби (а деколи і на інших частинах ) установлюють рухомий щит S , який закриває собою окремий сегмент переріз труби, регулює її пропускні можливості і швидкість протікання. Часто при використанні труби виникає потреба знайти найбільші значення цих величин.

Знайти, при яких значеннях щита S пропускні можливості труби і швидкість протікання найбільша.

2 w ³

Використаємо співвідношення:      v C ^{( )}u                (1)

v – швидкість течії, w – площа заповненого сегмента, u – довжина відповідної дуги, С – константа, що залежить від діаметра труби, її нахилу і шорсткості стінок ( Чугуєв Р.Р., Гідравліка, 1975р., ст.219 ).

Якщо R – радіус круга,  - центральний кут, що відповідає дузі, то застосувавши формулу довжини кола, площі кругового сегмента і співвідношення (1) , одержимо: v 1 sin 23

2CR(1  ) (2)

Таким чином, ця задача зводиться до математичної задачі – дослідження на максимум функції. sin

                                     f ( )  1 ,0   2 (3)



оскільки екстремуми функцій (2) і (3) досягається при одних і тих же значеннях . Функція (3) набуває найбільшого значення при , рівному кореню рівняння tg = , його краще розв`язати графічно. Одержимо  = 5,3 (304⁰ ). Це встановлюється на основі залежності 

Q vw^{ } 12CR(asin₂3 ^₎5³ , проводячи дослідження на максимум

функції.

Задачі на обчислення визначеного інтегралу.

  

Задача 1

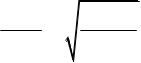
Знайти об’єм          двигуна автомобіля ,  якщо висота його поршня   80 мм,  а діаметр основи 7,8 мм. 

Розв’язання .

 

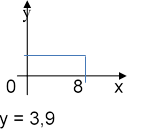3,9

V =  

 

    Задача 2

Для кращого обслуговування заїзду гонок серії «Формула-1» майстри визначили найкращий закон зміни швидкості руху автомобіля прямою трасою: v(t) = 60t – 0,3. Яку відстань проїде пілот гонки з 2 до 7 секунди від початку руху?

Розв’язання 

                s = )dt = =(30 ) = 30     - 0,1        – 

                - ( 30        - 0,1         ) = 30 (49 – 4) – 0,1(343 – 8) = 30  45 -0,1  335 =1350 –

33,5 = 1316,5(м)

Всі задачі подібні до цих не тільки сприяють ознайомленню учнів  з трудовими операціями, необхідними в названих професіях, але і закріплюють спеціальні математичні уміння. Наприклад навики усного рахунку, відсоткові розрахунки, знаходження об`ємів тіл і площ поверхні, максимуми і мінімуми функції.

 

Використання математичних розрахунків при підготовці до захисту дипломних робіт

Сучасний робітник повинен вміти числові дані підставляти у формулу, побудувати графік, зрозуміти та проаналізувати одержану відповідь, виготовити креслення, підрахувати кількість потрібного матеріалу. 

Щоб виконати завдання при підготовці до захисту дипломних робіт учні повинні зробити певні математичні розрахунки. Завдання можуть бути такого типу.

           Майбутні будівельники повинні вміти складати рецепти мастики, розчинів даного складу, розраховувати кількість плитки, яка необхідна для облицювання поверхні. Задача № 1

      Для облицювання приміщення полістирольними плитками необхідно 200кг каніфольної мастики, яка має склад у частинах:

1)   каніфоль – 1,7;

2)   спирт – 1,1;

3)   оліфа околь – 0,7;

4)   наповнювач (вапно) – 6,5.

       Наповнювач (вапно) у мастиці повинен складати  не менше 65%, розчинник –  не більше 12%. При недотриманні цих пропорцій мастика розшаровується. Скільки кілограмів кожної речовини необхідно для виготовлення  200кг мастики?

Розв’язання.

1.   Знаходимо скільки всього части приходиться на 200кг мастики:   

1,7 + 1,1 + 0,7 + 6,5 = 10(ч.)

2.   Знаходимо     масу,          яка    приходиться       на     одну      частину:              

200  : 10 = 20(кг)

3.   Знаходимо масу кожної речовини: 

Каніфоль: 1,7 × 20 = 34(кг)

Спирт: 1,1 × 20 = 22(кг)

Оліфа: 0,7 × 20 = 14(кг)

Наповнювач: 6,5 × 20 = 130(кг)

4.   Перевіримо виконання необхідних пропорцій: 

200  – 100%                                           200 – 100%    х – 65%                                                   х – 12%

    х = (200 × 65)/100 = 130(кг)     х = (200 × 12)/100 = 24(кг)

    Необхідна пропорція виконана.

У рецепті вказано 22кг, що менше 24кг, з чого випливає, що необхідна пропорція витримана.

      Відповідь:

Для одержання 200кг мастики необхідно: каніфолю 34кг; спирту 22кг; оліфи 14кг; наповнювач 130кг.

             Задача № 2

        Визначити площу керамічної плитки і кількість плитки, яка необхідна для обкладання підлоги, що має форму прямокутника розміром 2,3 × 3,1 м, якщо плитка має форму правильного шестикутника зі стороною а = 0,25м.

Розв’язання.

1.  Для обчислення площі плитки використаємо формулу для обчислення площі правильного шестикутника:

 

 

2.  Визначимо площу підлоги:

 

3.  Визначимо необхідну кількість плитки:

 

     Відповідь:

Для обкладання  підлоги  необхідно не менше 99 штук  плиток.

         Задача №3

На скільки збільшиться вартість штукатурки в даному приміщенні (а = 2,5м; в = 4м; с = 2,75м), якщо товщину штукатурного намету збільшити на 2мм; на 5мм?

Вартість одного мм штукатурного намету на 1 м² - 50грн. 

Розв’язання .

1.   Визначимо площу, яку необхідно поштукатурити: S = 2 · (а + в) · с =2 · (2,5 + 4) · 2,75 = 35,75 (м²)

2.   Якщо шар штукатурки збільшили на 2мм, то вартість кожного метра квадратного  збільшиться на 100грн С = 35,75 · 100 = 3575(грн.)

3.   Якщо шар штукатурки збільшили на 5мм, то вартість кожного метра квадратного  збільшиться на 250грн С = 35,75 · 250 = 8937,5(грн.)

         Відповідь;

При збільшенні шару штукатурки на 2мм вартість штукатурних робіт у даному приміщенні збільшиться на 3575грн.

При збільшенні шару штукатурки на 5мм вартість робіт збільшиться на 8937,5грн.

Завдання для майбутніх столярів, яке розвиває логічне мислення та сприяє вмінню ефективному і економному використанню в роботі потрібних матеріалів.

        Задача № 1

   Із круглої колоди діаметром d необхідно вирізати стойку прямокутного перерізу з найбільшою площею.  «Стойка» - елемент, який  працює на стикання. Найбільша площа перерізу балки необхідна для витримування  максимального навантаження.

 

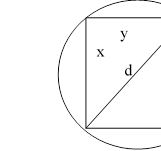
      Прямокутник вписаний в коло.

Розв’язання.

1.  Позначимо сторони прямокутника х і у. Тоді за теоремою Піфагора:                                            

2.  Площу прямокутника визначимо за формулою:

                                         

3.  Знайдемо похідну площі прямокутника:

                       

4.  Визначимо нулі функції:

,  , .

 

        5.Так як х – довжина прямокутника, х більше нуля, тому досліджуємо тільки один корінь.

В точці  похідна змінює знак з «+» на «- ».

Отже в цій точці функція набуває найбільшого значення. Тому при

       і              одержимо найбільшу площу     .

               Відповідь:

Переріз балки повинен мати форму квадрата зі стороною   .

                        Задача № 2

 Прямокутний дах довжиною 30м і шириною 12м. Кут нахилу скатів 30 градусів. Скільки матеріалу необхідно для його покриття? Як нахилені скати до горизонталі?

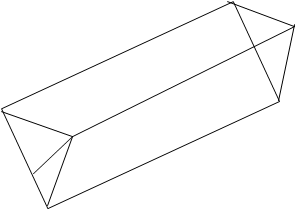                                                      D                                                                                                         

                                                                           F

 

                                        C

 

                A                                                               

              E

                                                          

                K

                             B

                Креслення двоскатного даху.

Розв’язання.

1.   Скати даху – це рівні прямокутники BCFE  та  ADFE.

2.   Прямокутник ABCD розташований горизонтально.

3.   Площини трикутників  ABE   і  CDF  перпендикулярні до площини прямокутника  ABCD.

4.   Так як скати даху – прямокутники, тоEF паралельна AD. Отже за ознакою паралельності прямої і площини EF паралельна площині ABCD.

5.   Скат BCFE утворює двогранний кут, ребро якого – ВС . Побудуємо лінійний кут двогранного кута. Проведемо ЕК перпендикулярно АВ, так як трикутник АВЕ перпендикулярний ABCD, то ЕК перпендикулярний ABCD. Похила ВЕ перпендикулярна ВС, отже і її проекція ВК перпендикулярна ВС. Отже кут АВЕ =β – лінійний кут двогранного кута, який утворений скатом BCFE і площиною ABCD.

Аналогічно можна довести, що кут ЕАВ – лінійний кут двогранного кута, який утворений скатом ADFE і площиною ABCD.

6.   Розглянемо трикутник АВЕ. Він рівнобедрений, отже кут ЕАВ дорівнює куту АВЕ, тому рівні і двогранні кути. Отже скати даху нахилені до горизонталі однаково.

7.   S = 2·ВЕ · ВС;

ВЕ = ВК/cos β = 6/cos30º = 6/0,866 = 6,93(м²);

S = 2 · 30 · 6,93 = 415,82(м²).

      Відповідь:  S = 415,82(м²), тому для покриття даху необхідно  не менше 416 м² матеріалу  без врахування з’єднаннь.

            Завдання до дипломних робіт кухарям – кондитерам  - це, переважно провести розрахунки у відсотковому відношенні.

   Задача №1

Розрахуйте кількість сировини для приготування 20 порцій борщу з урахуванням технологічної карти. ( Одна порція – 250мл)

Український борщ: рецепт

На 1 літр страви вам знадобиться, г:

Буряки – 150

Капуста білокачанна свіжа – 100

Картопля – 210

Морква – 50

Петрушка (корінь) – 20

Цибуля ріпчаста – 35

Томатне пюре – 30

Жир тваринний топлений харчовий – 20

Цукор – 10

Оцет 3% – 10

Борошно пшеничне – 6

Перець солодкий – 25

Сало шпик – 10

Часник – 4

Бульйон або вода – 700.

Розв’язання.

Рецепт даний на 1літр страви, що становить 4 порції.

1000 : 250 = 4

Для 20 порцій необхідно 5 літрів борщу.

4 · 5 =20

Щоб розрахувати кількість сировини для приготування 20 порцій страви необхідно масу кожного інгредієнта помножити на 5.

              Відповідь:

Для приготування 20 порцій борщу необхідно: буряки – 750г,капуста білокачанна свіжа – 500г, картопля – 1050г, морква – 250г, петрушка (корінь) – 100г, цибуля ріпчаста – 175г, томатне пюре – 150г, жир тваринний топлений харчовий – 100г, цукор – 50г, оцет 3% – 50г, борошно пшеничне – 30г,перець солодкий – 125г, сало шпик – 50г, часник – 20г, бульйон або вода – 3500г.

        Задача №2

Скільки котлетного м’яса можна отримати при поділі туші яловичини першої категорії угодованості, масою 120кг, якщо норма виходу котлетного м’яса до маси м’яса на кістках складає 40,3%? 

Розв’язання.

Складаємо пропорцію:

120кг – 100%

Хкг – 40,3%

 

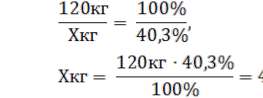
   Відповідь: 48, 36 кг котлетного м’яса.

             Спеціалістам з ремонту автомобілів часто доводиться мати справу із об’ємом двигуна із несправністю акумуляторної батареї. Тому майбутні автомобілісти повинні вміти визначати несправності механізмів і проводити розрахунки, щоб вчасно їх усунути.

       Задача № 1

          Розрахувати стан зарядженості АКБ, якщо відома температура повітря +30ºС, а густина електроліту становить 1,20г/см³. Зробити висновок.

Розв’язання.

     Залежність густини електроліту від температури повітря:

температура повітря	-30 ºС	-15 ºС	0 ºС	+15 ºС	+30 ºС
густина електроліту	1,27 г/см³	1,26 г/см³	1,25 г/см³	1,24 г/см³	1,23 г/см³

 

      Зміна густини нормально зарядженої АКБ може відбуватися в залежності від температури навколишнього середовища. Зміна температури на ±15 градусів змінює густину батареї на 0,01 г/см³. Зміна густин и на 0,01 г/см³ від норми зменшує заряд АКБ на 6,25%.

        Максимальний допустимий розряд батареї: влітку – до 50%, взимку – до25%.

         1,23 – 1,20 = 0,03( г/см³)

          3 · 6,25% = 18,75%           100% - 18,75% = 81,25%

          Відповідь:

Заряд АКБ більше 80% , а це допустимий розряд і влітку і взимку. Тому необхідності заряджати батареє немає.

          Задача №2

   Розрахувати робочий об’єм двигуна внутрішнього згоряння  КАМАЗ – 740, якщо відомо,що діаметр циліндра - 120мм, хід поршня - 120мм, кількість циліндрів – 8.

Розв’язання:

 Формула об’єму циліндра відома з геометрії:  V = πR²H.

Запишемо її відповідно до малюнку та умови задачі так:

.

Тоді об’єм двигуна   буде визначатися за формулою:

,        де  і - кількість поршнів двигуна, 

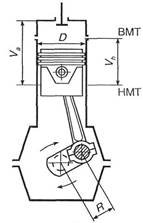         S – хід поршня,

         D – діаметр циліндра, 

         C – камера згорання,

         R – радіус кривошипа (R = S/2) ,

         ВМТ – верхня мертва точка, 

         НМТ – нижня мертва точка.

 

    

 

 

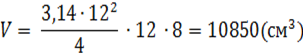
       Відповідь: 10850см³ ≈ 10,85л

 

Задачі професійного змісту з геометрії

 

Тема: Аксіоми стереометрії (будівельні професії).

Для того, щоб перевірити  чи є поверхня табуретки  або стіни плоскою, столяру потрібна лінійка, штукар користується правилом ? Як пояснити це з геометричної точки зору?

 

Тема: Паралельність прямих і площин (столяри ).

№1. Теслі потрібно розпиляти брусок, щоб площини були паралельні . Яку розмітку для цього необхідно робити ?

Тема: Перпендикулярність  прямих і площин(муляри).

№1. Необхідно побудувати котедж на схилі гори з кутом схилу 15°. Довжина будинку 9 м. На яку глибину треба зняти ґрунт  під фундамент?

№2. Довжина поперечки, на яку опираються стропила двокатного даху, дорівнює 15см. Знайти висоту даху, якщо відомо, що стропила з цією балкою утворюють кут 30°.

Тема: Кути між площинами (будівельні професії).

№1. Кромки кутів, відкосів і інших деталей будівель інколи оздоблюють стрічками шириною 30-50 мм. Під яким кутом до поверхні насікають стрічки зубилом ? Як називається цей кут ?

 

Тема: Піраміда

№1. Для перекриття русла річки при будівництві греблі виготовляють із бетону правильні трикутні піраміди масою 10 т. Висота і сторони основи такої піраміди пропорційні числам 5:2:6. Знайти лінійні розміри такої піраміди. (Густина бетону 2,22г\см³) .

Тема: Тіла обертання

№1 Скільки мідної проволоки діаметром 5 мм можна прокатати із мотка об'ємом 0,5 м³ ?

№2 Скільки тон породи в териконі висотою 90м, якщо відомо, що кут нахилу породи 46°, а її густина 2т/м³?

 

№3 Скільки квадратних метрів паперу в рулоні , висота і радіус якого відповідно 85 см, 45 см. і 2 см, якщо товщина паперу 0,1 мм? (За даними задачі знаходимо об'єм рулону, а знаючи об'єм паперу і товщину, знаходимо площину).

 

№ 4 Скільки тон стальних труб необхідно для того, щоб прокласти 48000 км  магістральних газопроводів , якщо для 1220 мм і товщиною 16мм?

 

№ 5 Знайти об'єм шахтового ствола діаметром 8 м, якщо його глибина 800м.

 

Тема: Об'єм паралелепіпеда

№ 1 Створення штучного гумусного горизонту, тобто родючого шару грунту із вмісткістю гумусу 4-5 % становить біля 5 тис. гривень за кубометр. Скільки буде коштувати господарству 1 га грунту товщиною 0,3 м?  (1га = 1000м²)

№ 2 За зміну бригада мулярів виложила 6000 цегли розмірами 25 см х 12 х 6,5  см. Обчислити заробіток бригади за зміну, якщо 1м³     кладки оплачується в  ... (Врахувати, що розчин збільшує об'єм на 15%) 

№ 3 Після висушування і випалювання об'єм цегли становить 75%  об'єму сирої цегли. Які повинні бути розміри сирої цегли, якщо розміри готової 25 х 12 х 6 см?

Тема: Об'єм призми

№ 1. При одному із способів захисту грунту від вимивання на схилах штампують лунки в формі прямокутного паралелепіпеда із квадратними основами ( сторона 50 см ) і висотою 10 см. Визначити скільки метрів води може зібратися в такій лунці на схилі з кутом нахилу в 10°, якщо :

а) одна із сторін основи лунки горизонтальна ;

б) одна із діагоналей основи лунки горизонтальна .

№2. Із стального прута, перерізом 45мм х 45мм треба викувати шість прокладок для гайок розмірами 50 мм х 50 мм х 25мм . Яку довжину прута треба взяти, припуск на обробку становить 6% об'єму прокладок.       

                                                                                                               

№3. Для  прокладки   залізничних шляхів    використовуються   рельси  довжиною 275 см, а поперечний переріз є на малюнку. Обчислити масу вантажу, якщо автокраном навантажено на платформу 600рейок, кількість підняття стріли крану. ( Густина дерега 0,8 г\см³)

16

18

15

26

 

№4. Розміри залізобетонної плити для рокриття 180 х 24 х580 см. Вздовж плити є 9 круглих скрізних отворів діаметром 10 см. Знайти масу плити , якщо густина бетону 2,2 г\см³ ?

        

№5. Підрахувати витрати розчину при укладці кахлів в приміщенні 6 х 4 м, якщо товщина стяжки 16 мм, товщина прослойки 7 мм. Скільки потрібно кахлів, якщо розміри кахлів 15 х 15 х 0,5 см?

№6. Розміри кузовів самоскидів МАЗ 205, ЗІЛ -130, відповідно дорівнюють (в м) 6,07x2,04x2,44;  6,72 х 2,39 х 2,18. Який з них має більший об'єм ?

 

Тема: Об'єми циліндра.

№1 Із деталі, що має форму правильної чотирикутної і трикутної призми, виготовили циліндри найбільшого об'єму. Яка кількість матеріалу піде у відходи в кожному випадку? 

 

№2 Паровий котел має довжину 8000мм із зовнішнім діаметром 4000мм. Яка кількість листів сталі марки Ст З КП необхідна для його виготовлення, якщо відомо, що лист сталі такої марки має розміри 6 х 1,5м?  В середині котла проходить чотири труби   

жарові          діаметром 400мм.       Обчислити загальний об'єм котла.

 

№3. (зварювальники)

Скільки в упаковці електродів для електрозварювання, якщо їх загальна маса 10 кг, а кожен електрод - це стальна проволока довжиною

45 см і діаметром 6 мм ? (густина = 7600кг\м³)

 

№4. (автослюсарі)

Скільки жерсті піде на погонний метр зливної труби діаметром

250мм, якщо на шви затрачується 8 % матеріалу? (848 мм²)

 

№5. (автослюсарі)

Якої довжини  треба  взяти   стальний   прут   із   стороною   40   мм   для виготовлення 40 молотків вагою 0,75 кг, кожен, якщо на обробку іде 6 % матеріалу ? (6,5 м).

№6. (автослюсарі, автокранівники)

Цистерна циліндричної форми має довжину 12м, діаметр основи 3,2 м. Скільки квадратних метрів металу пішло на її виготовлення ? На шви додати (4%). (12м²).

№7. (автослюсарі, автокранівники )

Потрібно виготовити 20 зливних труб довжиною по 8 метрів і діаметром 30см. Скільки листів заліза розмірами 142 х 71 см² піде на їх виготовлення. На шви додайте 10% .

№8. (автомобільні професії )

Визначити скільки квадратних метрів листа витрачено на виготовлення котла довжиною 4,2 м і зовнішнім діаметром   1,6 м. Через паровий котел проходить дві труби накалювання (що нагрівається від полум'я палива ) з діаметром по 40 см кожна.

№9. (автомобільні професії )

Цистерна має форму циліндра з діаметром основи 1,6 і висотою

6,2 м. Визначити вагу нафти, що наповнює цю цистерну. Густина нафти

0,8 г\см³  ?

 

№10. (сантехніки)

Визначити скільки води витікає за 1 год. через трубу, діаметром який дорівнює 84 см, якщо швидкість течії води 1 м/с .

№11. (автомобільні професії )

Із мідної заготовки, що має форму паралелепіпеда розмірами 1,2 х 0,32 х 0,32 м³ виготовляють дріт діаметром 2 мм . Визначити довжину дроту .

№12.(автомобільні професії)

Металева трубка має внутрішній діаметр 45 см, товщиною стінок 8 мм. Скільки тон труб необхідно, щоб провести водопровід довжиною 1,35 см? 

№13. (сантехніки)

Діаметр циліндра парової машини дорівнює в 30 мм, хід поршня

432 мм. Визначити об'єм робочої частини циліндра.

 

№14.(штукатури)

Визначити вартість фарбування конічного шпіля циліндричної башні, довжиною кола основи 8,8м, а кут між твірними конуса 60°. Вартість покраски 2м² =28гр .

№15.(автомобільні професії)

Знайти об'єм камери згоряння двигуна автомобіля ЗІЛ -130, якщо діаметр поршня 100 мм, а хід поршня 150 мм.

№16.(штукатури)

При нормі часу 0,79 год на 1 м² робітник вручну отштукатурив колону висотою 8 м за 4,8 год . Визначити діаметр основи цієї колони.

 

Тема: Об'єм конуса .

№1. (будівельні професії)

На будівельному майданчику пісок зберігають в штабелях . Пісок склали в штабель конічної форми, розміри якого слідуючі: довжина кола становить 32 м, довжина скосу 7 м. Знайти об'єм піску, враховуючи скиадку на вологість повітря.

№2.( будівельні професії)

Пісок складено в купи , майже конічної форми . Висота купи 1,8м, довжина кола основи 24,6 см. Скільки потрібно 5 т самоскидів для перевезення 12 куп піску, питома вага якого 1,6   т\ м³ ?

 

Тема : Об'єм кулі

 При захисті грунту від водяної   ерозії на схилах іноді роблять у лунки діаметром d Скільки води може зібратися в такій лунці на схилі з кутом нахилу  ?

Тема: Зрізаний конус

 Лунка має форму зрізаного конуса, діаметрами 600 і 300 мм, а висотою 500 мм. Скільки жерсті піде на її виготовлення , якщо не припуск додається 5% площі поверхні лунки ?

Тема: Бічна поверхня призми

 Для зрошування використовуються канали розмірами на малюнку, і товщиною стінок 25 см². Їх треба покрити бетоном. Скільки потрібно бетону, щоб покрити 1 км каналу?

25м

 

7м

Тема: Бічна поверхня піраміди

 Покрівля має форму піраміди із основою квадрат 4,5 х 4,5 м і кутом нахилу 45°. Скільки листів заліза розмірами 70 х 140 см треба для покриття даху, якщо відходи становлять 10% площі даху.

Тема: Бічна поверхня многогранників.

                    (будівельні професії)

Який час необхідно маляру для покраски панелі висотою 2 м в приміщенні, яке має розміри 2400 х 2700 х 5000мм маховою щіткою і валиком ,якщо норма часу для покраски 100м² поверхні щіткою - 6,4год, валиками - 3,4 год.

Тема: Площа бічної поверхні тіл обертання.

Знайти площу поверхні, яку потрібно очистити при ремонті реакційного котла циліндричної форми, якщо довжина котла 8м, а діаметр 3,5 м.

Задачі професійного змісту з алгебри

Розв’язування задач за допомогою складання рівнянь

 

         №1. Знайти лінійні виміри (довжину і ширину) ділянки прямокутної форми, якщо її периметр 30м, а площа 56м².

         №2. Катер проплив 9 км за течією річки і 14 км проти течії річки, витративши на весь шлях стільки часу, скільки йому потрібно для подолання 24 км в стоячій воді. Знайдіть швидкість катера в стоячій воді, якщо швидкість течії річки 2км/год.

      №3. Дві бригади працюючи разом закінчили асфальтувати дорогу за 4 дні. Скільки днів було б потрібно на виконання цієї роботи кожній бригаді окремо, якщо одна з них могла закінчити асфальтувати дорогу за 6 днів раніше, ніж друга.

      №4. Вкладник поклав до банку 1000 грн. За перший рік йому нарахований відсоток річних, який другого року збільшений на 2%.У кінці другого року на рахунку було 1188 грн. Скільки відсотків становила банківська ставка першого року?

     №5. До розчину, що містить 40 г солі, додали200 г води, після цього його концентрація зменшилась на 10%. Скільки води містив розчин і яка була його концентрація?

 

Розв’язування задач на відсоткові розрахунки

        №1. Клієнт взяв в банку кредит в розмірі 50 000 грн. на 5 років під 20% річних. Яку суму клієнт повинен повернути банку в кінці року?        №2. Два приятелі поклали в банк по 10000 грн. кожен, причому перший поклав вклад з щоквартальним нарахуванням 10%, а другий – щорічним нарахуванням 45%. Через рік приятелі отримали кошти разом з нарахованими процентами. Хто отримав більший прибуток?

№3. Протягом календарного року зарплата кожного місяця підвищувалась на одне й теж саме число гривен. За червень, липень, серпень зарплата складала 9900 грн., а за вересень, жовтень і листопад 10350 грн. Знайдіть суму зарплат за весь рік.

     №4. Книжковий магазин сплачує видавництву 90% вартості, позначеної на обкладинці книги, а реалізує книгу за зазначеною ціною. Скільки відсотків складає націнка магазину?  

      №5. Планом було передбачено, що підприємство протягом декількох місяців буде виготовляти 6000 одиниць продукції. Збільшивши продуктивність праці, підприємство стало виготовляти на 70 0диниць більше, ніж було передбачено, і на місяць раніше встановленого строку перевиконало завдання на 30 одиниць. Протягом скількох місяців було передбачено виготовити 6000 одиниць продукції.

 

Задачі з використанням регіонального компоненту.

Алгебра

1.       AT „Ворскла "виготовляє костюми. На виготовлення одного костюма іде 3,5 м тканини. В одному рулоні 40 м. тканини Скільки потрібно рулонів для виготовлення замовлення із 150 костюмів?

2.       На ДОК виготовляють вікна у формі прямокутника із півкругом зверху. Периметр вікна 8 м. Яке повинно бути співвідношення ширини і висоти прямокутної частини вікна, щоб воно пропускало найбільшу кількість світла?

3.       Для відновлення  паркового ландшафту виділили площу  1,6 га . Площа висадки одного дерева  4 х 4 м. Першого року посадили  100 дерев, а кожного наступного по 90 дерев. Через скільки років буде засаджено всю площу?

 

Геометрія

Паралельність прямих і площин 

1. Навести приклади взаємного розміщення прямих, прямої  і площини та площин у навісному та підземному переході міста.

          Перпендикулярність прямих і площин

1. Назвати перпендикуляри  і похилі, які є в конструкції навісного наземного мосту.

 

Об'єми многогранників

1. Підземний центральний перехід м. Полтави має форму прямокутного паралелепіпеда, лінійні виміри якого 55м, 100м, 6м. Скільки потрібно вантажних машин, щоб вивезти землю, якщо за 1 раз машина вивозить 30 м³ землі?

Об'єми тіл обертання

1.  На заводі  виготовляють лампи денного освітлення. Зовнішній діаметр цих ламп 40 мм, а внутрішній 38мм, довжина лампи 80 см. Скільки матеріалу потрібно для виготовлення таких ламп партією із 500 штук.?

2.  Знайти об'єм алмазного круга виготовленого на Полтавському заводі алмазних виробів , діаметр якого 60 см і товщина 3 мм.

3.  Цистерни, виготовлені на заводі „Хіммаш” мають

довжину 12 м, діаметр 3,2 м. Скільки бензину можна перевезти потягом із 30 цистерн , якщо густина його 0,7·10³кг/м³?

 

Бічна поверхня многогранників

1.            Бічні стіни центрального переходу покриті мармуровою плиткою розмірами 40 х 30 см. Яка кількість плитки потрібна, щоб покрити стіни, якщо виміри переходу 55 х 100 х 6 м.

2.            Купол підземного переходу виготовлений у вигляді півсфери . Скільки потрібно склопластика для його покриття, якщо діаметр купола 17м.

3.            Навісний надземний перехід в районі Київського вокзалу  м.Полтави виготовлений із склопластику у формі пустотілого циліндра. Довжина мосту 90 м, ширина 3м. Скільки потрібно склопластику для його виготовлення ? 

Поверхня тіл обертання

1.           Завод виготовляє фарфорові вази циліндричної форми діаметром 10см. і висотою 25 см. Скільки емалі піде на зовнішнє покриття партії ваз із 100 штук, якщо на 1 м² іде 180 г емалі ?

2.           Чашка, яку виготовляють на фарфоровому заводі, має форму зрізаного конуса, радіуси основ його 3 см і 6 см і висота 10 см. Знайти повну поверхню чашки.

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Література:

1.  Бевз Г.П., Бевз В.Г. Математика ,  11// Київ. «Генеза» - 2012 -317с.

2.  Бевз Г.П., Бевз В.Г. Математика , 10 // Київ. «Генеза» - 2010 -270с.

3.  Вінник Л. Міжпредметні зв’язки як умова підвищення ефективності навчально-виховного процесу// Професійно-технічна освіта. – 2003. - №2. – 43с.

4.  Волошина Л. Інтеграція змісту загальноосвітньої та професійної підготовки // Професійно-технічна освіта. – 2008. - № 1. – 21с.

5.  Євтушенко О. Професійне спрямування вивчення математики // Професійно-технічна освіта. – 2008. - № 3. – 30с.

6.  Висоцька Л. Інтеграція навчання - одна з важливих форм удосконалення навчально-виховного процесу. .//Профтехосвіта.2013.-№9-7-10с.

7.  https://proftekhosvita.org.ua/uk/news/..

8.  metodportal.net/node/788