Захист проекту: "Функція навколо нас"

 

Проект « Функція навколо нас»

 

Тип проекту: інформаційно-пошуковий.

Проблема: Залежність між величинами в математиці, фізиці, медицині і т.д.

Мета проекту:

• зібрати інформацію про функцію;
• встановити залежність між величинами в математиці, фізиці, медицині і т.д.;
• дослідити графіки функцій.

Завдання проекту:

• Організація інформаційно-пошукової роботи учнів з означеної проблеми.

      -  Проведення презентації проекту .

 Етапи реалізації проекту

Діагностико-концептуальний:

Створення і визначення функцій пошукових груп.

Розподіл доручень між керівниками та учасниками проекту.

Пошук джерел інформації з поданої теми.

Організаційний:

Збір матеріалів з науково-популярних видань.

 Збір матеріалів при спілкуванні з медиками, працівниками торгівлі.

Систематизація та оформлення отриманого матеріалу.

Практичний:

Проведення досліджень з фізики.

Створення комп’ютерної презентації проекту

 Проведення презентації проекту у формі семінару.

Очікувані результати

Формування знань про функцію.

Вдосконалення життєвих компетентностей учнів: інформаційної, соціально-трудової, вміння вчитися.

Формування навичок дослідницької роботи.

Вдосконалення вміння орієнтуватися в інформаційному просторі та аналізувати отриману інформацію.

Створення ілюстративних та інформаційних матеріалів.

 

Сценка

 

Сидить учень. Дивиться в щоденник.

Понеділок. Алгебра. Означення функції «2»

Вівторок. Алгебра. Графік функції «2»

Понеділок. Алгебра. Властивості функції „2" Пантоміма

Входить мама, бачачи щоденник в розпачі. З великої бутили „Валер'яна" великою ложкою п'є.

Кличе батька.

Входить батько з ремінцем. Виховує сина. П'є валер'янку. Виходить. Вносять стопи підручників і приковують сина до столу. Виходять. Син намагається вчити, замріюється.

 

Танок функцій

Учень прокидається і пише лист.

Конституційному суду України

Учня 9 класу Васильківської СЗШ № З Ткача Максима

 

Заява

Прошу вилучити з програмового шкільного матеріалу тему „Функція" як непотрібну в життєвих ситуаціях.

01.12. 2007 року Підпис

 

 

Заклеює в конверті і відправляє.

Урок суд

Секретар суду. Встати! Суд іде! Прошу сідати. Оголошується склад суду.

Голова - світило шкільної математики учениця 11 класу Лелеко Вікторія Вікторівна.

 

Члени суду: від шкільної громадськості Ткач Володимир Валерійович, від учительської Зубко Надія Олександрівна.

Головний суддя.

Сьогодні слухається справа з обвинувачення Функції, вона звинувачується в тому, що 1) привласнила право на способи завдання: табличний, графічний, словесний, напівграфічний; 2) існує в декількох формах: обернені функції, складні, елементарні, однозначні, обмежені та необмежені, монотонні, парні і непарні, періодичні, по модулю; 3) з її вини виникли точки перетину графіка з координатними осями, точки перегину і екстремуму; 4) намагається розширити знання учнів з точних наук, зменшуючи час відпочинку.

Ввести підсудну!

Ваше прізвище. Рік вашого народження.

 

Підсудна. Функція. Рік народження цього означення - 1718.

 

Суддя. Слово надається прокурору.

 

Прокурор. Ще на зорі людської діяльності Функція, скориставшись своєю можливістю впливати на розум людей, підло здійснювала чимало підступних дій в усіх галузях практичної діяльності людини, навіть у таких традиційно не математичних як управління виробництвом, біологія, медицина. Прошу суд заборонити використання функції в наш час.

 

Адвокат. Ваша честь! Протестую проти обвинувачення!

 

Суддя. Протест не приймається.

 

Прокурор. Є докази, зібрані членами творчої групи математичного гуртка.

Секретар. Будь ласка, докази слідства.

(докази слідства (фільм) Застосування функції в роботі, медицині)

 

Фільм

„Гастроном"

Грачова Ірина Олександрівна - реалізатор.

Я маю справу з величинами залежними від інших так, що із змінюванням перших змінюються і другі.

Наприклад.

Кількість товару і його вартість. 300г цукерок коштує.........

а 500г цих же цукерок коштує........

Вартість товару і плата за нього за 1 кг ковбаси я одержу...........

а за 1 кг ковбаси

Більша кількість покупців за робочий день, більше реалізовано товару -зростає мій відсоток прибутку.

Допомагають мені графіки величини попиту, які побудувала моя донька Катерина, учениця Васильківської СЗШ № 3.

 

 

„Районна центральна лікарня "

Я, Жданова Світлана Вікторівна, медична сестра терапевтичного відділення стверджую: функція працює на наше здоров'я.

Графічне зображення діяльності серця - кардіограма є, по суті, вектор-функцією, що містить 12 або 18 компонентів, кожний з яких є числовою функцією часу. Тому лікар, який вивчає кардіограму пацієнта, працює в 12-або 18-вимірному просторі.

Створено математичні моделі роботи окремих органів людини і процесів, які відбуваються в її організмі. Аналіз цих математичних об'єктів (графіків, рівнянь, нерівностей, матриць, графів і т.д.) допомагає лікарям ефективніше здійснювати профілактику й лікування різних захворювань. Наприклад, відомо, що після інфаркту міокарда інколи катастрофічно порушується серцевий ритм -виникає так звана фібриляція, що спричиняє смерть буквально через кілька хвилин. Математики розкрили таємницю цього небезпечного явища і допомогли знайти нові можливості запобігти катастрофі.

При виборі методу лікування деяких хвороб доводиться звертатися до математичного програмування. Нехай є дві можливості лікувати якусь хворобу -променева і хімічна терапія. Ефективність кожного методу виражена в якихось загальних одиницях. Наприклад, лікувальний препарат має ефективність 1000 одиниць, а опромінювання - 1000 одиниць за хвилину. Припустимо, що для одужання хворому потрібно не менше 3000 одиниць ефективності. Враховуючи, що обидва методи токсичні, їх не можна застосовувати необмежено.

Отже, треба так скомбінувати обидва методи лікування, щоб завдати хворому якнайменше незручностей.

 

 

 

„ Фельдшерсько-акушерський пункт "

  Тимошенко Людмила Амосівна, фельдшер.

Номограма, подана на малюнку, допомагає перевіряти відповідність маси людини її зростові. На лівій шкалі знаходять точку, яка відповідає фактичному зросту, а на правій -точку, що відповідає об'єму грудної клітки. До знайдених точок прикладають край лінійки. Точка перетину краю лінійки із середньою шкалою дасть шукану масу. Відхилення від цього на + 3 кг для чоловіка і на +3,5 кг для жінки вважається нормальним.

Даний графік показує залежність стану хворого від його температури.

Адвокат. Прошу слова. Потрібно врахувати, що Функція дала змогу людині навчитися встановлювати залежність між величинами, моделювати закономірності перебігу явищ природи. Я вважаю, що найкраще про формування характеру малютки функції можуть розповісти її батьки. Будь ласка, свідоцтво про народження.

Секретар. Батьки: Архімед, Декарт, Лібніц, Ейлер, Лобачевский, Соболев,

Діріхм .

Адвокат прошу суд заслухати свідків - батьків функції. Секретар. Запрошуємо свідків. Свідок 1. Декарт Рене.

Всі довго чекали народження Функції, бо цього вимагало життя. Я ввів у математику змінну величину і прямокутну систему координат, на основі змінної величини виникли нові математичні науки, які допомогли відповісти на багато запитань техніки, мореплавства, артилерії, геодезії.

Дбаючи про долю доньки Функції - пов'язав алгебру з геометрією.

Свідок 2. Ферма П'єр.

Наша мала пречудова, бо завдяки їй я мав змогу розвинути метод координат, ввести рівняння прямої і кривих другого порядку. Вивчати процеси диференціювання і інтегрування. Вивчити формулу інтегрування по частинам, правило знаходження екстремуму функції.

Свідок 3. Лейбніц Готфрід Вільгельм

Наше миле дитя я назвав функцією, крім цього запропонував основні терміни математичного аналізу - диференціал, алгоритм, абсциса, координати. Дав визначення диференціала, інтеграла, розробив правило диференціювання сили, різниці, добутку, частки. Функція допомагала мені при вивченні руху сил, створення механізмів.

Свідок 4. Бернуллі Іоганн.

Весь свій час я розвивав здібності та таланти Функції в області диференційованого та інтегрального обчислення, розкрив поняття функції як аналітичного виразу, що складається з змінних і постійних. Ввів формулу розкладу функції в степеневі ряди.

Свідок 5. Коллі Огюстен.

Донечка Функція дала змогу мені створити теорію функцій комплексного змінного, розвинути теорію рядів, визначити поняття неперервності функції, ввести загальні властивості функції для будь-якого значення об'єкта.

Суддя. Чи будуть запитання до свідків батьків функції.

Прокурор. Ні, Ваша Честь. У мене питання до суду. Чи братиметься до уваги те, що батьки обвинуваченої були такими видатними людьми?

Суддя. Ці факти справи не стосуються.

Прокурор. Як можна пояснити, те що функція постійно міняє своє обличчя, то вона лінійна функція, то квадратична, чи степенева чи . При цьому знову і знову змінює поведінку і характер. То спадає, то зростає чи неперервна, чи навіть періодична.

Адвокат. Це легко пояснити.

Функція - особо різнопланова розвинута. А щоб зрозуміти все, треба не лінуватися, а більше з нею спілкуватися. І моя мета і моєї підзахисної вам в цьому допомогти. Тож дозвольте запросити свідків.

Свідки 1,2,3,4 (матем)

Числова множина X називається симетричною, якщо для довільного х є X число - х є X, наприклад множина цілих чисел, відрізок [- а; а ], інтервал [- а; а ], інтервал - та ін. - множини, симетричні відносно початку координат.

Функція f, визначена на симетричній множині X, називається парною, якщо для х є X виконується рівність

F (- х) = f(x),

Наприклад: у = х², у = cos х, у = | х |, у = f (| х |).

Функція f, визначена на симетричній множині X, називається непарною, якщо для х є X виконується рівність

F (-x) = -f(x),

Наприклад: у - х , у =tg х, у = /х/

                            2х

Поняття періодичної функції стане зрозумілішим на прикладі окремих Нехай f визначена на множині X. Якщо існує Т = 0 таке, що для х є X числа

х + Т і х - Т також належать множині X і f (х + Т) =f (х) (f ( х - Т) = f (х)), то

функцію f називають періодичною з періодом Т.

 

Приклад. Функції sin х і cos х мають період, де n = ± 1, ±2, ±3,... Що сума і добуток двох функцій з одним і тим самим періодом Т є функціями з періодом Т. зазначимо при цьому, що якщо число Т було найменшим додатним періодом двох заданих функцій, то після їх додавання чи множення Т може перестати бути найменшим із додатних періодів.

 

Приклад. Функції f1 (х) = 3 sin х + 2 і f₂ (х) = 2 - 3 sin х мають найменший період 2, а їх сума f1 (х) + f₂ (х) = 4 найменшого періоду не має.

Пояснюється на таблицях з графіками даних функцій

 

Суддя. Прошу Вас, займіть місця. Ми заслухали вчених-батьків, розглянули питання про класифікацію функцій, способи завдання функції. Надаю слово підсудній.

Функція.

Мене звати Функція, я встановлюю залежність змінної у від змінної х, при якій кожному значенню х відповідає єдине значення у. на світі не існує змінних величин, які б змінювалися ізольовано без зв'язку з іншими величинами. Взагалі то з моєю допомогою можна описати нескінченну різноманітність процесів і явищ реального світу. Я завжди беру приклад зі своїх батьків, бо вони в мене люди творчі, обдаровані. Вони завжди ставилися до всіх людей з повагою, мали гармонійні стосунки в сім'ях. А також мали різнопланову діяльність в галузях науки, наукову ерудицію та всебічність захоплень. В мене багато друзів-чисел, можна сказати від - и до + оо . маю наставників де область визначення та область значень, які регулюють значення незалежної змінної X, та залежної.

Прокурор. Шановний суддя, ви бачите, що функція попала під вплив осіб, які не поважають всі числа. Вона порушує правила спілкування. Прошу прослухати

СВІДКІВ.

Свідок 1.

У таблиці показано область значень деяких елементарних функцій.

 

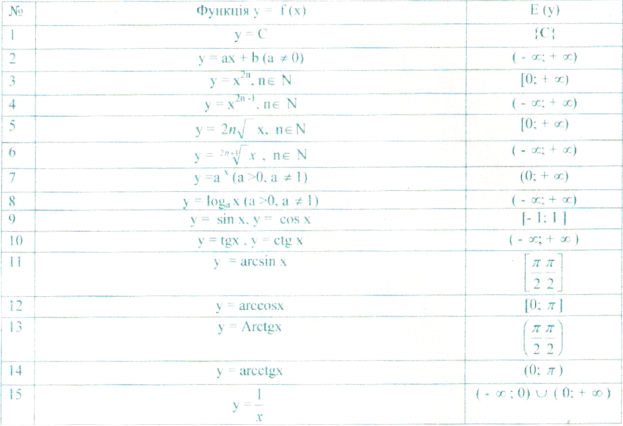
Моя мета показати типові методи знаходження області значень функції. Іноді область значень функції можна встановити із означення функції.

Приклад 1 . у = | х| = х, х > 0,

                              - х, х > 0.

З означення функції зрозуміло, що у може набувати будь-яких невід'ємних значень. Отже, Е(у) = [0; ∞).

 

Приклад 2. у = [ х ] - найбільше ціле число, яке не перевищує дійсне число х (ціла частина х).

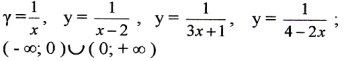
Зрозуміло, що у може набувати будь-яких цілих значень. Отже, Е (у) =z.

 Адвокат. Прослухавши свідків я думаю ви всі прийшли до висновку, що Функція не порушує правил, а навпаки більш повно розкриває нам відомі правила: на 0 ділити не можна, корінь існує тільки з додатного числа і т.д. Крім цього хочу відзначити, що без Функції ми не змогли б знайти швидкість, шлях, прискорення, об'єм, площу, тиск.... Не змогли б використовувати всім відомі закони Бойля-Маріотта, Гука Ньютона, і т. д. Тобто без поняття Функції наука не змогла б розвиватися. Крім цього вона тісно пов'язала такі науки, як фізика, хімія, біологія, географія. І створила умови для більш повного розвитку медицини, техніки, транспорту, економіки.

Прошу заслухати свідків.

Проекти з фізики

Проект №1

Мій проект присвячений рівноприскореному рухові тіла, були розглянуті питання функціональної залежності швидкості, переміщення координати від часу, а також графіки кінематичних величин. Для установлення зв'язку кінематичних величин та понять мовою математики була складена таблиця

 

Мовою механіки	Позначення та формули	Поняття мовою математики
Час	t	Незалежна змінна,
		аргумент
Координат	X	Залежна змінна
Закон руху тіла	X=f (t)	Функція
Інтервал часу

 

Використовуючи знання з алгебри -

S = t² +20t

а = -1   b-20

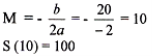
Вершина параболи по формулі

 

Виконуємо побудову

 

Задача

Швидкість руху тіла задана рівнянням V = 20-21 Побудувати графіки проекції швидкості та переміщення 1)У = 20 - 2\ - лінійна функція Для побудови достатньо вибрати дві точки

 

t	V
0	20
10	0

2) Формула швидкості для рівно прискореного руху V= V1 + аt.

Отже V о = 20 м/с

а = -2 м/с²

Формула переміщення

Отже

Ми отримали формулу переміщення, що являється квадратною функцією, де t- незалежна змінна, S - залежна змінна. Виконаємо побудову.

3) Для знаходження вершини параболи використовуємо формули

Проект №2

Мій проект був присвячений визначенню залежності напруги джерела струму від навантаження.

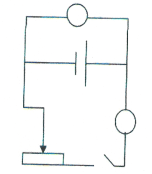
Для дослідження була використана схема:

 

Яка складається з амперметра, вольтметра, джерела струму, реостата, ключа. Спочатку вольтметром було визначено ЕРС джерела струму (за умови розімкнутого кола).

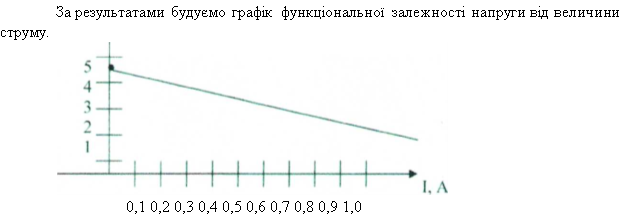За допомогою реостата змінюємо значення нагрузки і покази амперметра та

 

І (А)	0	0,2	0,4	0,6	0,8	1,0
V(В)	4,5	4,1	3,6	3,2	2,8	2,4

Якщо продовжити пряму до перетину з горизонтальною віссю координат -точка А, можна знайти величину струму короткого замикання. Напруга в даній точці буде дорівнювати нулю, а сила струму досягла свого максимального значення.

Проект №3

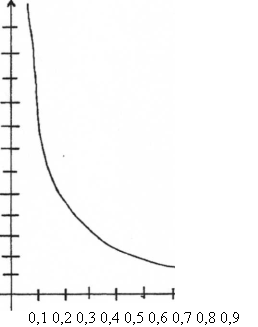
В своєму проекті присвяченому використанню поняття функцій в фізиці я розглядала тему „Графічне зображення ізопроцесів".

Це дало змогу встановити функціональну залежність між тиском, об'ємом та температурою.

Ізотерма газу виражає обернено пропорційну залежність між тиском і об'ємом. Таку криву в математиці називають гіперболою. Ізобара, характеризує лінійну залежність об'єму газу від температури і графіком являється пряма. Тиск газу також лінійно залежить від температури.

 

Проект №4

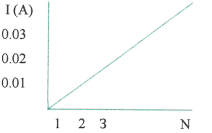
Мій проект був присвячений вивченню напівпровідникового фотоелемента. Були проведені дослідження, які дали змогу встановити функціональну залежність величини створеного струму від відстані між джерелом світла та фотоелемента.

 

Цм)	1	0,5	0,3	0,2
І(А)	0,01	0,04	0,11	0,25

 

Причиною збільшення струму є збільшення концентрації електронів і дірок. За допомогою графіка було встановлено прямо пропорційну залежність сили струму фотоелемента від кількості ламп, тобто джерел світла.

 

Крім цього було установлено, що величина фотоелектрорушійної сили не може бути більшою різниці потенціалів електричного поля . Тому при збільшенні освітлення фотоелемента його ЕРС спочатку зростає, а потім досягає стану насичення.

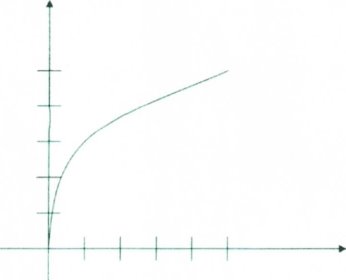
1000 2000 3000 4000 5000 Е

 

Тема мого проекту «Застосування методу координат»

Виявляється координатний метод має широке застосування під час розв'язання багатьох практичних задач.

Представник першої бригади. Застосування методу координат в інженерній практиці тісно пов'язане з розв'язуванням геодезичних задач. Такі задачі виникають під час прокладання гірських тунелів, лісових доріг, чагарникових просік, тобто в тих випадках, де неможливо безпосередньо зробити усі необхідні вимірювання. Існують дві основні геодезичні задачі - пряма й обернена, що часто використовуються під час проведення робіт у важко - доступних місцях.

Задача . Через гірський масив треба прокласти тунель. За планом місцевості його початкова точка А (40; 15), а кінцева - В (80; 45). Знайти довжину тунелю та азимут, під яким треба прокладати тунель.

 

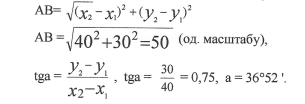
Відповідь. 50 од., 36°52 '.

Останнім часом великого значення надається збереженню довкілля. Серед багатьох наукових методів використовується і метод математико-картографічного моделювання. Він полягає в тому, що за допомогою аерокосмічних апаратів з великих територій збирається різноманітна інформація про стан довкілля, як-от: стан продуктивності сільськогосподарських угідь, стан здоров'я лісового масиву, розміри ділянок суші чи моря, забруднених промисловими викидами, тощо. Із зібраних даних складають математичні моделі, досліджують їх і відповідно до висновків пропонують заходи щодо покращення стану довкілля. ,

Перш за все, треба знати площі масивів, що досліджуються. Часто інформацію про форми ділянок подають у координатній формі. Тому треба вміти визначати площі фігур, заданих своїми координатами.

Загальновідомо, що найпростішою функціональною залежністю між двома змінними величинами х та у є лінійна залежність

у = кх +b,

Де к та b - параметри.

У біології лінійна залежність між двома змінними зустрічається досить рідко. Проте за певних умов залежність між двома змінними інколи можна описати лінійною функцією.

Наприклад, на певному проміжку часу (зокрема на ранній стадії) розвитку риби її довжина лінійно залежить від віку: L = br, де L - довжина, t - час, b - параметр (коефіцієнт пропорційності), що залежить від виду риби та знаходиться за даними натуральних спостережень. Якщо відомо, що довжина даного виду риби в віці одного року дорівнює 15 см, то

Таким чином, для даного виду риби L =151

Більш цікавим є застосування в екології функції оберненої пропорційності

Ця залежність застосовується для математичного моделювання стосунків типу „хижак-здобич". Зокрема, такі стосунки мають популяції зайців та вовків:

де N - кількість популяції зайців, п - кількість популяції вовків, k -параметр, що визначається на підставі даних натуральних спостережень. Наприклад, якщо в певний момент часу було зафіксовано N=120 та п =30, то k = 120-30 = 3600,

отже, кількість зайців залежно від кількості вовків можна визначити за

формулою

Широко застосовується за математичного моделювання розмноження популяції показникова та логарифмічна функції. Зокрема, відомо, що розмноження більшості бактерій описується такою експоненційною показниковою залежністю

 

де N - кількість бактерій у момент часу t, N_о - початкова кількість бактерій,

г - константа швидкості розмноження бактерій, що визначається експериментально, е - основа натуральних логарифмів (е ~ 2,71828...).

 

Математика допомагає передбачати приріст та динаміку росту насаджень. Залежність між об'ємом гілки дерева і її діаметром виражається рівнянням параболи четвертого степеня і єдина для різних порід дерев. При конструюванні

дерева природа скористалась аналогом теореми Піфагора: квадрат радіуса основного стовбура дорівнює сумі квадратів радіусів складових стовбурів, виміряних вище від розгалуження. Об'єм усієї надземної частини дерева залеяшть від єдиного параметра - діаметра стовбура.

При різних стихійних лихах люди й тварини ховаються в лісі, під деревами або на деревах. Справді, середнє дерево діаметром стовбура 60 см здатне витримати 600-900 кг плодів, а під час урагану - тиск повітряного потоку до 7-8 тис. кг. Якщо спроектувати всі гілки дерева (без листя) на вертикальну площину, то сумарна площа їх тіні називається захисною площею дерева. Вона й захищає від вітру все, що знаходиться за деревом, - поля, луки, шосе, залізниці і т.д. Величина захисної площі дерева теж залежить від діаметрів гілок і стовбурів.

І ще один цікавий факт. Стовбури й гілки дерев не завжди круглі. Так, в однорядній смузі з тополь виміряли діаметри стовбурів у напрямі, паралельному переважаючим вітрам, і в напрямі, перпендикулярному до них. Виявилося, що діаметри стовбурів мали форму еліпса, великий діаметр якого був паралельним напряму з переважаючими вітрами. Отже, дерево розраховує, як будувати себе, щоб раціональніше використати власний будівельний матеріал. Може, скоро скористаємося цим патентом природи, зводячи споруди в місцях з постійними напрямками переважаючих вітрів.

Здається, що природа сама турбується про збереження своїх найцінніших витворів, підвищуючи надійність функціонування живих організмів у міру їх ускладнення. На графіку N - загальне число представників деякого виду на Землі; п - число клітин у даному організмі; п N - загальне число клітин в усіх організмах даного виду на Землі. На осях у подвійному логарифмічному масштабі відкладену залежність загального числа клітин в усіх організмах певного виду від числа клітин, що утворюють один організм, тобто від складності організму.

Для порівняння зазначено лінійні розміри організмів. Найбільше клітин мають ссавці, особливо людина. Людей на Землі менше, ніж найпростіших організмів, але „людських клітин" значно більше, ніж усіх одноклітинних організмів. Це означає, що з ускладненням організмів надійність існування їх елементарних складових клітин значно збільшується.

З давніх-давен слово „хижак" уособлює все негативне. Ще недавно в сільських районах можна було бачити щити із закликом „Убий вовка!". Вважали, що їх потрібно вбивати скрізь, і чим більше, тим краще. Потім виявили парадоксальну ситуацію. В місцевостях, де знищували вовків поголовно, кількість травоїдних різко зростала, але скоро так само різко падала.

Біологи й математики пояснили цей парадокс тим, що в природних умовах вовки знищують не так уже багато, причому насамперед слабких, хворих тварин. Знищуючи неповноцінних тварин, вовки тим самим виконують функцію санітарів і забезпечують необхідну кількість розвинених, здорових тварин, які дають здорове потомство.

Математики побудували математичні моделі співіснування видів, один з яких є хижаком відносно іншого. Його описує система двох диференціальних рівнянь, дослідження якої показують, що хижак повністю не знищує інший вид, а види співіснують, періодично змінюючи свою чисельність. -

Математичним втіленням формули квітки є наприклад, рівняння кривих, нагадуючи пелюстки квітки.

Формула цветка

Сплелись в клубок запутанные трассы

рабочих пчел, и оводов, и ос.

Разгул цветов.

Сплошное буйство красок.

Неразбериха полная. Хаос.

Но это только кажется снаружи.

Лишь озаряясь познания огнем,

мы изнутри

порядок обнаружим,

строжайший строй

в нестройности найдем.

И станет ясным листьев бормотание,

и пляска пчел у тесного летка,

и, разглядев растение,

ботаник

изобразит нам

формулу цветка.

Леонид Вышеславский

 

Суддя. Ми заслухали всіх свідків з боку звинувачення та збоку захисту. Надаю слово Функції.

Функція. Упродовж тисячоліть я давала змогу людям можливість пізнавати закони навколишнього світу і розумно використовувати їх у своєму житті. І в усі часи знаходилися яскраві й одержимі, різні за характером, темпераментом і долею особистості, які завжди були темпераментом і долею особистості, які завжди були вірні своїй справі. І я надіюся, що молодше покоління учнів буде старанно вивчати мої властивості, класифікацію, графіки. І це дасть змогу їм стати мудрими, всебічно розвиненими, творчими особистостями. І можливо виникнуть нові типи функції, бо все іде вперед, розвивається і я надіюсь на нове в своєму житті. Тож дорогі учні давайте пізнавати світ разом.

Прокурор. Я хочу підвести підсумок розглянутому. Вчені які вивчали функцію і вивчають діти Франції, Німеччини.

Адвокат. Протестую, бо наші українські вчені внесли багато нового при дослідженні властивостей функції. І тому поняття функції інтернаціональне, і без нього не можливий розвиток жодної країни. Запросіть будь-ласка свідків.

Повідомлення учнів. На комп'ютер проектуються їх фотографії вчених.

 

Марченко Володимир Олександрович (07.07.1922р.)

Народився в Харкові, в 1945 р. закінчив Харківський університет. Працював в інституті низьких температур АН УРССР.

Основні напрями дослідження - теорія диференціальних рівнянь, теорія диференціальних рівнянь, теорія функцій, функціональний аналіз.

Розв'язав ряд задач по теорії апроксимації неперервних функцій по всій дійсній осі теорії майже періодичних функцій.

Островський Іосіф Володимирович (06.04.1934р.)

Народився в Дніпропетровську, закінчив в 1956 році Харківський університет. Основні роботи присвячені теорії функції, теорії ймовірностей.

Досліджував зв'язки асимптотної поведінки мераморфної функції з розподіленням її значення по аргументу, аналітичні характеристики функцій ймовірного розподілу.

 

Ахіезер Наум Ільїн (06.03.-1901 -03.06.80)

Закінчив Київський інститут народної освіти в 1923 році. З 1928-1933 р. працював в Київському фізико-хіміко-математичному інституті. З 1933-1974-1 в Харківському інституті.

Дослідження присвячені теорії функцій, функціональному аналізу, інтегральним рівнянням, теорії моментів. В своїх працях висвітлив ряд питань теорії наближень функцій поліномами, що мають відхилення від нуля.

 

Бережанський Юрій Макаровим (08.05.1925 р.)

Народився в м.Києві, в 1948 році, закінчив київський університет, де й продовжив потім свою роботу.

Основні дослідження відносяться до функціонального аналізу, теорії диференціальних рівнянь з похідними. Вперше розглянув обернену задачу для рівнянь спектрального аналізу, довів теорему для рівняння Шріодингера. Побудував теорію розкладу по узагальненим власним функціям, а також теорію позитивно визначених ядер по власним функціям.

 

Бондар Микола Герасимович, 19 грудня 1920р.

Народився в Києві, в 1943 році закінчив Дніпропетровський інститут інженерів залізничного транспорту. З 1946 року працював в цьому ж інституті.

Основний напрям роботи - будівельна механіка. Крім цього розробив метод змінного масштабу для перетворення нелінійних функцій в лінійні. Досліджував пружність систем за умови їх не лінійності. Розв'язав ряд задач про коливальні системи при в'язкому, сухому, турбулентному опорі.

 

Букрєєв Борис Якович (5 вересня 1859 - 2 листопада 1962р)

В 1882 році закінчив Київський університет. З 1889 працював в даному університеті.

Основні дослідження відносяться до геометрії, варіційному численню, теорії функції. В 1889 році дослідив фуксові функції нульового рангу з симетричним основним полігоном. Вивчав диференціальні параметри, вперше застосував до них симетричні координати.

Воронець Петро Васильович (8.07.1871-27.10.1923)

Закінчив київський університет в 1896році. Роботи відносяться до диференціальних рівнянь, векторного аналізу, динаміки. Ввів рівняння руху систем в формі функцій, які залежать від часу, а також лінійних функцій узагальнених швидкостей.

 

Гливенко Валерій Іванович (2.01.1897-15.02.1940)

Народився в Києві, закінчив Московський університет в 1925 році.

Основні напрями робіт - математична логіка, теорія функцій, теорія ймовірностей. В теорії функцій і теорії множин дав означення границі і і вивчав неявні функції, визначених за допомогою нерозривних функцій.

 

Гончаров Василь Леонідович (24.09.1896-30.10.1955)

Народився в Києві, закінчив Харківський інститут народної освіти. Працював в Харківському фізико-хіміко-математичному інституті.

Основні дослідження відносяться до теорії функції (комплексного змінного, наближення функцій полігонами).

Розглянув ряд теорем для мероморфних функцій, побудував графіки цілих функцій першого порядку, що мають границю менше від . Проводив дослідження по інтерполірованню цілими функціями.

 

Данилюк Іван Ілліч

Народився в с. Рашков Івано-Франківської області в 1955 році закінчив Львівський університет. Працював в Донецькому інституті прикладної математики та механіки.

Основні напрями досліджень - рівняння математичної фізики, аналітичні функції, теорія сингулярних інтегральних рівнянь. Розв'язав нелінійну задачу із вільною границею, визначив умови і критерії існування нетривіальних розв'язків.

 

Дзядик Владислав Кирилович (18.11.1919)

Народився в с. Сахновщина Харківської області. Закінчив Дніпропетровський університет в 1951 році. З 1953-1960 працював в Луцькому педагогічному інституті, з 1963 - в київському університеті.

Головний напрям досліджень - теорія функцій. Побудував теорію наближених значень в абсолютно монотонних функціях, визначив верхні границі наближень для класів функцій, які мають обмежену похідну будь-якого порядку, і

 

Коваленко Анатолій Дмитрович (16.01.1905-19.09.1973)

Народився в Києві, в 1929 році, закінчив Київський політехнічний інститут. Працював в Київському політехнічному інституті.

Основні дослідження відносяться до теорії пружності і термопружності. Розробив термодинамічні основи теорії термопружності, в теорії спеціальних функцій ввів і дослідив гіпергеометричні функції другого порядку.

Корнійчук Микола Павлович

Закінчив Дніпропетровський університет в 1955 році, з 1974 року працював в інституті математики АИ УССР.

Дослідження відносяться до теорії функцій. В теорії наближених функцій розв'язав проблему Фавара, розробив нові методи розв'язування екстремальних задач. Розв'язав проблеми нелінійної апроксимації.

 

Суддя. Ми заслухали всіх свідків зі сторони звинувачення та з боку захисту. Надаю слово Функції.

Функція. Упродовж тисячоліть я давала змогу людям можливість пізнавати закони навколишнього світу і розумно використовувати їх у своєму житті. І в усі часи знаходилися яскраві й одержимі, різні за характером, темпераментом і долею особистості, які завжди були вірні своїй справі. І я надіюся, що молодше покоління учнів буде старанно вивчати мої властивості, класифікацію, графіки. І це дасть змогу їм стати мудрими, всебічно розвиненими, творчими особистостями. І можливо виникнуть нові типи функції, бо все іде вперед, розвивається і я надіюсь на нове в своєму житті. Тож дорогі учні, давайте пізнавати світ разом.

Секретар. Суд іде радитися. Прошу всіх встати!

Секретар. Встати! Суд іде! Суддя. Суд виносить вирок.

1. Визнати Функцію невинною у висунутих обвинуваченнях. Звільнити підсудну з-під варти у залі суду.
2. Для запобігання катастрофічним наслідкам не використання знань про Функцію, зобов'язати всіх учнів школи старанно вивчати Функцію, а також науки, де використовуються поняття Функції.,

Секретар. Засідання суду вважати закритим.