Заняття № 25 на тему «Точка перетину медіан трикутник (центр мас). Точка перетину висот трикутника (ортоцентр)»

Заняття №25  на тему «Точка перетину медіан трикутника (центр мас). Точка перетину висот трикутника (ортоцентр)»

Дане заняття відповідає діючій програмі факультативного курсу з математики для 7 класу Бевз В. Г, Бурда М. І., Прокопенко Н. С. «За лаштунками шкільної математики». Воно містить теоретичний матеріал, що відображає тему, приклади завдань з розв'язками та вправи для самостійного виконання.

Враховуючи інтереси та нахили учнів, їхню підготовленість, вчитель може доповнювати зміст заняття додатковим матеріалом, змінювати та удосконалювати методику проведення.

Тема 3. Особливі точки та лінії в трикутнику.

Геометричні побудови

Заняття 25

Точка перетину медіан трикутника (центр мас). Точка перетину висот трикутника (ортоцентр)

Медіана трикутника — це пряма проведена через вершину і середину протилежної сторони і ділить трикутник на два однакової площі. Три медіани перетинаються в одній точці, яка називається центроїдом трикутника. Ця точка також центр мас трикутника: якби трикутник був зроблений із дерева, то можна було б тримати рівновагу тримаючи за центроїд. Центроїд ділить кожну медіану у співвідношенні 2:1, наприклад відстань між вершиною і центроїдом вдвічі більша ніж між центроїдом і протилежною стороною.

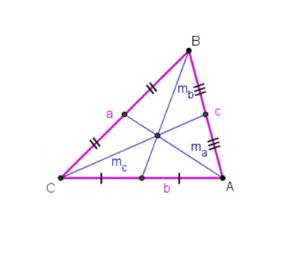Властивості медіани трикутника:

Медіана поділяє трикутник на два трикутники з рівними площами, а три проведені медіани — на шість рівновеликих.

Медіани трикутника перетинаються в точці, яка є його центром мас.

Медіана прямокутного трикутника, проведена до гіпотенузи, ділить трикутник на два рівнобедрені трикутники, та дорівнює половині гіпотенузи.

В точці перетину медіани трикутника діляться в відношенні 2:1.

При перетворенні медіана переходить в медіану.

Якщо дві медіани трикутника перпендикулярні, то сума квадратів сторін, на які вони опущені, у п'ять разів більша за квадрат третьої сторони.

Формули медіани:

• Довжина медіани визначається з рівняння:,

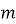
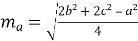де — сторона трикутника, на середину якої опущена медіана; — інші сторони трикутника.

• Сума квадратів медіан довільного трикутника становить 3/4 від суми квадратів його сторін.
• Довжина сторони трикутника через медіани визначається наступним чином: ,

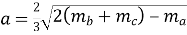де медіани до відповідних сторін трикутника, — сторони трикутника.

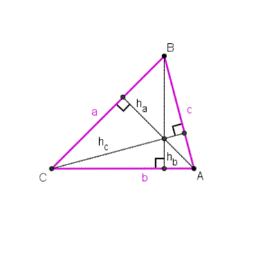Висота трикутника — пряма проведена з вершини і перпендикулярна до протилежної сторони або до продовження протилежної сторони. Ця сторона називається основою трикутника. Точка перетину сторони і перпендикуляра називається основою перпендикуляра. Довжина висоти — це відстань від вершини до основи трикутника. Три висоти перетинаються в одній точці, яка називається ортоцентром трикутника. Ортоцентр лежить всередині трикутника (і відповідно всі основи перпендикулярів лежать в трикутнику) тоді і тільки тоді, якщо трикутник не тупокутний (в ньому жоден з внутрішніх кутів не більший за прямий кут).

Розв’язування задач та вправ

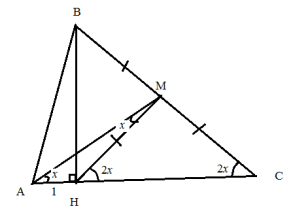•   Відрізки АМ і ВН відповідно медіана і висота гострокутного трикутника АВС, АН=1, Знайти ВС.

Розв'язання.

Проведемо медіану НМ, ВН=МС=МН, то , бо – рівнобедрений. то – рівнобедрений, то НМ=1, то ВС=2.

Відповідь. 2

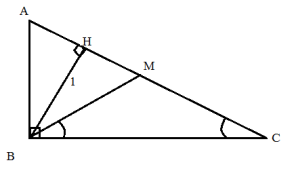
•             Знайдіть гіпотенузу прямокутного трикутника з кутом 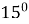, якщо висота опущена на гіпотенузу 1.

Розв'язання.

ВМ – медіана, то АМ=МС=ВМ. – рівнобедрений, то

Розглянемо , то

Відповідь. 4

Завдання для самостійного розв’язування.

1. (Якоб Штейнер). На відрізку АВ як на діаметрі побудовано півколо з невідомим центром. Всередині півкола дано точку К. За допомогою однієї лінійки проведіть з точки К перпендикуляр до АВ.
2. Всі вершини гострокутного трикутника АВС недоступні. Знайдіть ортоцентр трикутника
3. Довести, що бісектриса кута А є бісектрисою кута ОАН (де ∙ – центр кола, описаного навколо трикутника ABC).

 Використана література

1. Адлер А. Теорія геометричних побудов, Переклад з німецької Г. М. Фіхтенгольца. Видання третє. Л., Навчпедвид, 1940—232 с.
2. Бевз Г. П. Геометрія трикутника. — Київ: Генеза, 2005. — 120 с. ISBN 966-504-431-1
3. Бевз Г. П., Бевз В. Г., Владімірова Н. Г. Геометрія: Підручник для 7-9 кл. — Київ: Вежа, 2004. — 309 с. ISBN 966-7091-66-Х
4. Воронець О. М. Геометрія циркуля, Популярна бібліотека з математики під загальною редакцією Л. О. Люстерника, М.- Л., ОНТІ, 1934 — 40 с.
5. Кушнір І. А. Трикутник і тетраедр в задачах: кн. для вчителя / І. А. Кушнір. — К. : Радянська школа, 1991. — 208 с.
6. Манін Ю. І., Про розв'язність задач на побудову за допомогою циркуля та лінійки, Енциклопедія елементарної математики книга четверта (геометрія), М., Фізматвид, 1963. — 568с.
7. Петерсен Ю. Методи і теорії розв'язку геометричних задач на побудову, Москва, типографія Э.Ліснера та Ю.Романа, 1892 — VIII + 114с.
8. Прасолов В. В.. Три класичні задачі на побудову. Подвоєння куба, трисекція кута, квадратура кола. М.: Наука, 1992. 80 с. Серія <Популярні лекції з математики>, випуск 62.
9. Щетников А. І. Як було знайдено де-які розв'язки трьох класичних задач древності? Математична освіта, № 4 (48), 2008, с. 3-15.
10. Слива Н. В.Математика 7клас. Факультативний курс http://www.fak-matematika_7_klas_sliva_n.v.