Заняття "Алгоритм Прима-Краскала"

Тема. АЛГОРИТМ ПРИМА – КРАСКАЛА

Мета: ознайомити учнів з алгоритмом Прима - Краскала на прикладі його реалізації мовою Паскаль, розвинути уявлення учнів про сфери використання алгоритмів, сприяти вихованню інформаційної культури учнів.

Хід заняття

I. ПРОБЛЕМНА МЕТА

ЗАДАЧА (поставлена у загальному виді у 1961 році незалежно Примом і Краскалом)

В країні Хохляндії потрібно з'єднати N міст оптоволоконними лініями для розширення мережі Internet, Всі відстані між містами відомі. Знайти найменшу можливу довжину ліній.

II. ОТРИМАННЯ ТЕОРЕТИЧНИХ ВІДОМОСТЕЙ

Граф - це схематичне зображення об'єктів, пов'язаних відношеннями між собою. Такі об'єкти на графах називають вершинами, а відношення, що їх пов'язують, - ребрами.

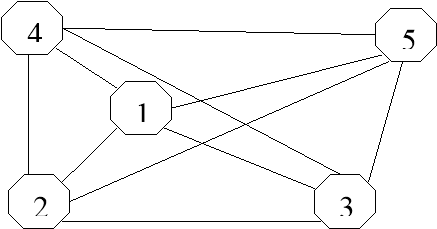Граф у Turbo Pascal можна задати двовимірним масивом d, де кожен елемент d(i,j) - відношення, яке пов'язує і-ту та j-ту вершини. Для розв'язку поставленої задачі потрібно пронумерувати міста від 1 до N та занести в двовимірний масив відстані між містами (довжини доріг). Для пошуку найменшої довжини ліній потрібно використати жадібний алгоритм: вибирати в циклі щоразу найменшу довжину дороги при умові, що цю дорогу ще не вибирали.

III. ЗАКРІПЛЕННЯ   ОТРИМАНИХ ЗНАНЬ

У файлі data.in записано число N - кількість міст у Хохляндії, та N рядків по N чисел - відстані між містами. Вивести у файл data.out найменшу довжину ліній та послідовність пар міст, які потрібно з'єднати оптоволоконними лініями. (N<50).

ВХІДНИЙ ФАЙЛ data.in

5

0 3 5 2 7

3 0 3 7 5

5 3 0 10 4

2 7 10 0 4

7 5 4 4 0

ПРОГРАМА

program prime_crascal;

var d: array[1..50,1..50] of real;

 f: text;

 x, y: array[1..50] of real;

 col: array[1..50] of integer;

 res: array[1..50,1..2] of integer;

 dmin, l: real;

 n, k, m, i, j, i1,j1:integer;

begin

 assign(f, 'data.in');

 reset(f);

 readln(fn);

 for i:=l to n do

  for j:=l to n do

   read(f, d[i,j]);

 close(f);

 for i:=l to n do

  col[i]:=i;

 k:=0;

 l:=0;

 while k<n-l do

  begin

   dmin:=maxint;

   for i1:=l to n-1 do

    for j1:=i1+1 to n do

     if (d[i1, j1]<dmin) and (col[i1]ocol[j1]) then

      begin

       dmin:=d[i1,jl];

       i:=i1;

      end;

   k:=k+1;

   l:=l+dmin;

   res[k,1]:=i;

   res[k.2]:=j;

   j1:=col[j];

   for m:=l to n do

    if col[m]=j1 then col[m]:=col[i];

  end;

 assign(f, 'data.out');

 rewrite(f);

 writeln(f,l:4:2);

 for i:=l to n-1 do

  writeln(f,res[i,1],res[i,2]:5);

 close(f)

end.

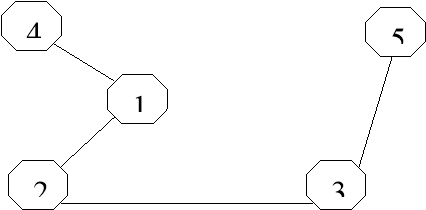
РЕЗУЛЬТУЮЧИЙ ФАЙЛ

data.out

12.00

1 4

1 2

2 3

3 5

IV. ДОМАШНЄ ЗАВДАННЯ

Розглянути роботу програми при інших вхідних файлах. Розглянути шляхи покращення програми.