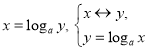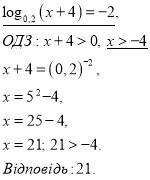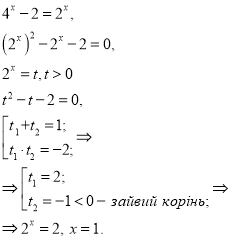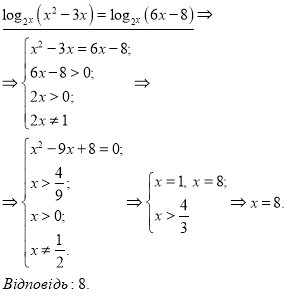Заняття "Розв'язування найпростіших логарифмічних рівнянь"

Тема : Розв’язування найпростіших логарифмічних рівнянь.

Мета: формування умінь студентів розв’язувати логарифмічні рівняння різними методами:

• метод потенціювання; зведення логарифмів до однієї і тієї самої основи; метод заміни;
• метод логарифмування;
• виховувати математичну грамотність при оформленні розв’язання логарифмічних рівнянь.

Інтерактивні методи: презентація « Логарифмічна функція. Графік. Область визначення логарифмічної функції»; «Застосування логарифмічної  функції»- актуалізація опорних знань, «Мозговий штурм»  - підсумок  заняття.

Тип заняття: засвоєння нових знань

Наочність та обладнання: роздатковий матеріал, дидактичний матеріал, проектор.

Розробив  викладач математики  Дубовик І.Ф.

Хід заняття

І.Організаційні моменти

ІІ. Перевірка домашнього завдання

 -  Перевірити відповіді домашніх вправ з використанням презентації;

 -  Дати відповіді на запитання, які виникли під час виконання домашніх вправ.

ІІІ. Актуалізація опорних знань.

• студент презентує «Логарифмічна функція. Графік. Область визначення логарифмічної функції»

	Коментарі
	Доповідь студента:  Дає означення логарифмічної функції.  Для побудови графіка логарифмічної функції розглянемо показникову функцію . Дана функція є монотонною на всій області визначення а значить вона має обернену. Для знаходження аналітичного задання оберненої функції, виразимо змінну х через у скористувавшись означенням логарифма числа. Отримаємо: . Отже, логарифмічна функція є оберненою для показникової. Для побудови графіка логарифмічної функції скористаємось алгоритмом побудови графіка оберненої функції.
	Побудуємо графік показникової функції, вважаючи, що ; Побудуємо пряму , яка є бісектрисою І та ІІІ чвертій; Відобразимо графік

 

Завдання 1: Знайти область визначення логарифмічних функцій

• Студенти групи виконують самостійно завдання відповідно до варіанту (варіант* - для студентів, які встигають на достатній, високій рівні)

І варіант	ІІ варіант	ІІІ варіант*
Знайти ОДЗ

• Студент презентує застосування логарифмічної функції .( презентація «Застосування логарифмічної  функції)

ІV. Формулювання теми, мети і завдань заняття

Таким чином, ми бачимо, що логарифмічна функція широко застосовується в природі,  в усіх напрямках людської діяльності. В фізиці, біології складаються рівняння, в яких присутні логарифмічні функції. Для отримання результату ці рівняння необхідно вміти розв’язувати. А все складне починається з самого простого. Отже..

Формулюється тема, мета й завдання заняття.

План

1. Означення логарифмічного рівняння.
2. Види найпростіших логарифмічних рівнянь та способи їх розв’язання.
3. Приклади.

 

V. Засвоєння поняття найпростіших логарифмічних рівнянь. Методи  їх розв'язування.

Означення: Логарифмічним рівнянням називається рівняння, які містять змінну під знаком логарифма.

Приклади логарифмічних рівнянь:   , і т.д.

Розв’язати логарифмічне рівняння – це означає знайти всі його корені або довести, що рівняння не має коренів.

Примітка: При розв’язуванні логарифмічних рівнянь можуть використовуватись такі перетворення, які приводять до сторонніх коренів. Тому, потрібно обов’язково виконати АБО перевірку кожного із одержаних коренів АБО знайти область допустимих значень рівняння.

Найпростіші логарифмічні рівняння та методи їх розв’язання

• Пояснення викладача. Робота біля дошки під керівництвом викладача ( для п.2, 3). Таблиця проектується на дошку.

	Вид рівняння	Приклад
		Розв’язує студент під керівництвом викладача
		Коментарі викладача: Підлогарифмічна функція має «складний вигляд» тому знаходження можна опустити. Але після знаходження коренів ОБОВ’ЯЗКОВО потрібно виконати перевірку підставивши отримані значення в ісходне рівняння. Перевірка:
		Розв’язує викладач з коментарями
		Розв’язує викладач з коментарями

 

• Робота біля дошки під керівництвом викладача.

Вправа 1:  Розв’язати логарифмічні рівняння  .

• Виконання (продовження) самостійної роботи на занятті:

І варіант	ІІ варіант	ІІІ варіант*
Розв’язати рівняння

 

Вправа 2:  Розв’язати логарифмічне рівняння .

• Виконання (продовження) самостійної роботи на занятті:

І варіант	ІІ варіант	ІІІ варіант*
Розв’язати рівняння

 Вправа 3:  Розв’язати логарифмічне рівняння

• Виконання (продовження) самостійної роботи на занятті:

І варіант	ІІ варіант	ІІІ варіант*
Розв’язати рівняння

 

VІ. Підсумок заняття

• «Мозговий штурм» Якій метод можна застосувати для розв’язування логарифмічних рівнянь

Завдання: Дано рівняння

	Вид рівняння	Записати рівносильне рівняння або систему.

 

VIІ. Домашнє завдання

• Опрацювати конспект заняття Тема 2-12; заповнити фрейм ( дивитись додаток 1)

• Розв'язати вправи: ( Математика 11 клас, Бевз)

Завдання Установити відповідність між рівняннями та їх коренями

 

 

 

 

 

Самостійна робота на занятті тема 2.12

Число __________ Група _________ Варіант __________

І варіант	ІІ варіант	ІІІ варіант*
Знайти ОДЗ

 

 

І варіант	ІІ варіант	ІІІ варіант*
Розв’язати рівняння

 

 

 

 

 

І варіант	ІІ варіант	ІІІ варіант*
Розв’язати рівняння

 

 

 

І варіант	ІІ варіант	ІІІ варіант*
Розв’язати рівняння

 

 

	Вид рівняння	Записати рівносильне рівняння або систему.

Підсумок заняття