заняття з математики "Многогранники. Правильні многогранники"

Про матеріал

Подано конспект заняття на тему "Многогранники. Правильні многогранники", з якої розпочинається розгляд розділу "Многогранники. Об'єми та площі поверхонь многогранників" на ІІ курсі. В конспекті підібрано вправи, які готують та мотивують студентів до сприйняття нового матеріалу, розкрито зміст вивчення основних понять та їх осмислення. Вказано завдання для закріплення матеріалу: усні вправи та задачі, які вимагають рисунка та письмових пояснень.

Перегляд файлу

Міністерство освіти і науки України

Вищий комунальний навчальний заклад

"Коростишівський педагогічний коледж імені І.Я.Франка"

Житомирської обласної ради

План – конспект заняття

з математики (геометрії), проведеного у 123 групі

Викладач Дітківська В.М.

- 2018 -

Тема . Многогранники. Правильні многогранники.

Мета . Ознайомити студентів з поняттям про многогранники та їх

основними елементи, з поняттям про правильні

многогранники , їх основні властивості;

розвивати спостережливість, логічне мислення, просторову

уяву студентів;

виховувати математичну культуру мовлення студентів,

інтерес до вивчення математики, естетичні смаки.

Наочність та обладнання: моделі многогранників, моделі правильних многогранників, ноутбук, проектор, мультимедійна дошка

Тип заняття: засвоєння нових знань

Хід заняття

І. Організація студентів до заняття

ІІ. Повідомлення теми і завдання заняття

З поняттям многогранника учні ознайомлюються ще в початковій школі. Звернемося до підручників з математики першого та четвертого класів.

Ви переконалися, що учні початкових класів мають уяву про многогранники та геометричні тіла.

Сьогодні на занятті ми поглибимо знання про многогранники, з’ясуємо їх основні елементи та познайомимось з правильними многогранниками.

ІІІ. Сприймання і усвідомлення нового матеріалу

Фігури, які вивчає стереометрія, називаються тілами. Наочно тіло уявляють як частину простору, зайняту фізичним тілом і обмежене поверхнею (демонструю моделі многогранників).

Многогранником називається тіло, обмежене скінченою кількістю плоских многокутників. Многокутники, які обмежують многогранник називаються його гранями, їх сторони - ребрами, а вершини - вершинами многогранника. Давайте обстежимо тіла (куб, піраміда) та з’ясуємо кількість граней, форму граней, кількість ребер та вершин.

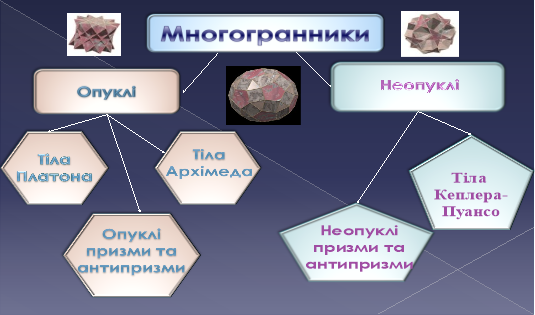
В стереометрії розглядають опуклі та вгнуті многогранники. Опуклим називається многогранник, якщо він лежить по один бік від площини кожного з плоских многокутників на його поверхні.

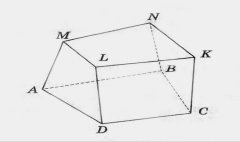
11 копия.jpg

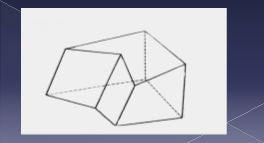
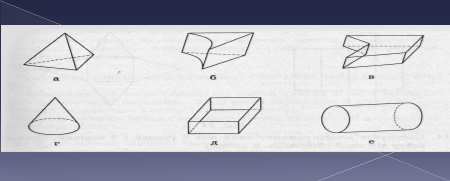
Многогранники в оточуючому середовищі зустрічаються дуже часто. Знання властивостей многогранника необхідне багатьом фахівцям. Наведіть приклади предметів побуту, які мають форму многогранників.

Якщо поверхню многогранника розрізати по кількох його ребрах і розкласти на площині, то дістанемо розгортку даного многогранника. На слайдах подані розгортки многогранників.

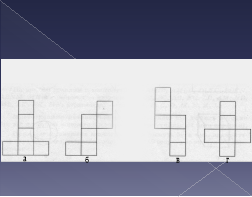
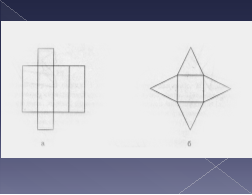
Подумайте і скажіть як називаються многогранники розгортки яких зображено на слайдах.

(Розглядаємо моделі многогранників).

- Серед представлених многогранників вкажіть такий, який має чотири грані. Покажіть грані, вершини, ребра.

- Яке найменше число ребер може мати многогранник? (6).

- Покажіть многогранник, який має п’ять граней і шість вершин (трикутна призма).

- Вкажіть многогранник у якого число граней і вершин однакові (трикутна піраміда).

- Скільки ребер може сходитись у вершині многогранника (довільне число, але не менше трьох).

- А зараз нагадаємо як знайти площі поверхні многогранників за підручником четвертого класу.

Правильні многогранники

Правильним многогранником називається такий опуклий многогранник, гранями якого є правильні многокутники з однаковою кількістю сторін, а в кожній вершині сходиться однакова кількість ребер.

Працюючи над проектом "Правильні многогранники", група дослідників шукала відповіді на такі питання:

- Скільки видів правильних многогранників?

- Як вони називаються?

- Чому отримали таку назву?

- Які властивості мають?

- Які многокутники є гранями тіла?

- Який вигляд має розгортка правильного многогранника?

- Чи можна в природі та побуті зустріти такі многогранники?

Про результати пошукової роботи ми сьогодні дізнаємося (звіт груп з використанням слайдів).

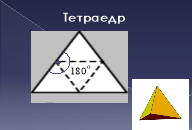
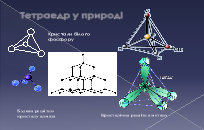
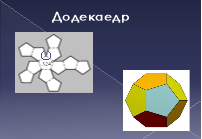
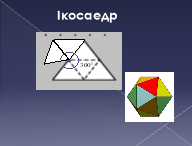
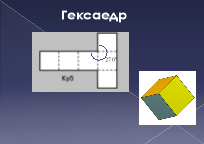
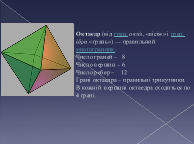
Ми з’ясували, що існує лише п’ять типів правильних многогранників гранями яких є правильні трикутники, квадрати, п’ятикутники. Але крім правильних трикутників, чотирикутників, п’ятикутників є ще інші правильні многокутники. Невже неможна використати дані правильні многокутники утворивши нові правильні многогранники? Над цим питанням задумувалися вчені різних епох. Ще Евклід у своїх "Началах" довів, що є лише п’ять типів правильних многогранників. Але математики продовжували пошуки: одні шукали нові види правильних многогранників, інші - доведення неможливості створення нових видів таких тіл.

У 1939 році російський учений - математики академік Александров довів теорему, яка свідчить, що "Сума плоских кутів, які сходяться в одній вершині, для будь - якого многогранного кута менша за 360 градусів".

Вона дає можливість дати відповідь на питання про існування лише п’яти типів правильних многогранників, які ще називають тілами Платона тому, що вони займали важливе місце в філософії про будову Всесвіту. Правильні многогранники вважались "космічними тілами" і кожному з них було присвоєне найменування однієї зі стихій, що складали на думку греків, основу буття.

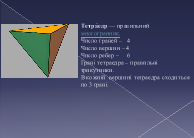
Тетраедр - вогонь, тому що його вершина спрямована вгору;

ікосаедр - воду, тому що він самий обтічний;

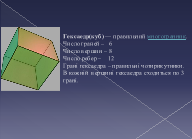
куб - землю, як самий стійкий;

октаедр - повітря, як самий "повітряний";

додекаедр - втілював у собі "все суще", вважався головним, символізував світобудову.

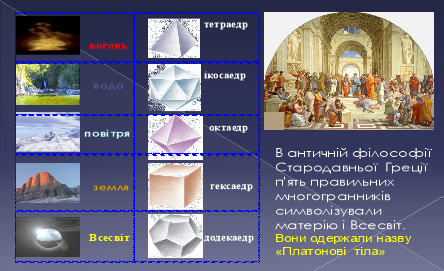
Основні характеристики правильних многогранників занесемо до таблиці.

(робота в групах)

- Давайте знайдемо скільки буде, якщо від суми кількості вершин і граней відняти кількість ребер (В + Г - Р). Для будь - якого правильного многогранника цей вираз дорівнює 2. Першим до цього висновку прийшов у своїх дослідженнях відомий математик XVІІ століття Леонард Ейлер, який народився у Швейцарії, а жив у Росії і працював у Петербурзькій академії наук. Тому рівність В + Г - Р = 2 називається Ейлеровою характеристикою правильних многогранників.

ІV. Закріплення і застосування набутих знань

а) Завдання для усної роботи.

1. Площа однієї грані правильного тетраедра дорівнює 15 см². Чому дорівнює площа повної поверхні тетраедра?

2. Площа повної поверхні додекаедра дорівнює 240 см². Знайдіть площу однієї грані.

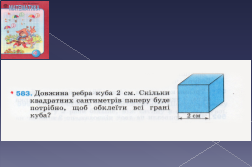
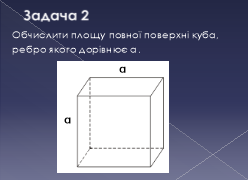
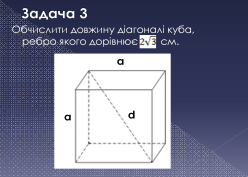
3. Ребро куба дорівнює 4 см. Чому дорівнює відстань між протилежними гранями куба?

Знайдіть площу бічної поверхні куба? Знайдіть площу повної поверхні куба?

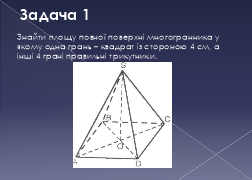
4. Знайдіть площу повної поверхні многогранника, що складається з чотирьох рівних граней, кожна з яких є правильним трикутником і стороною 2 см.

б) Практичні завдання.