Застосування інтегралу




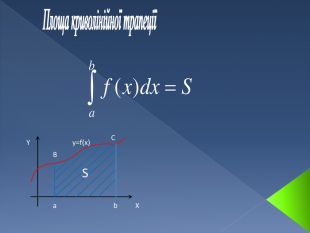
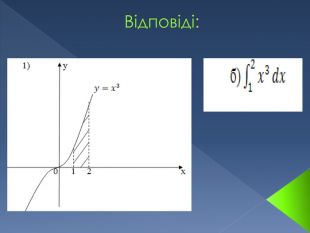
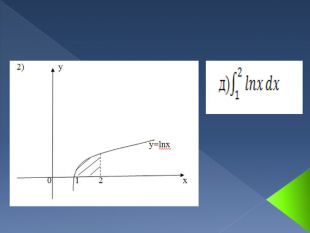
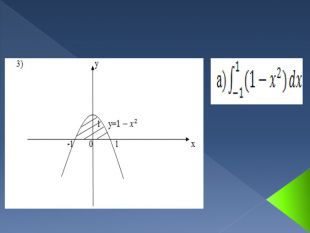
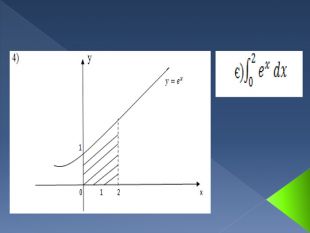
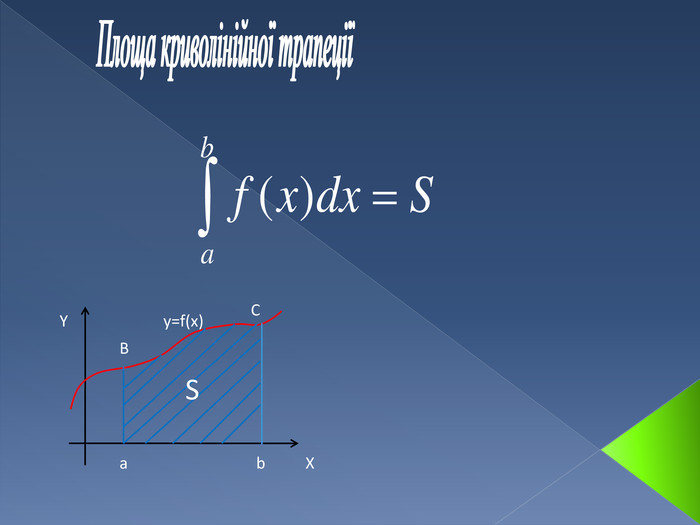
![Криволінійна трапеція та її площа. Криволінійною трапецією називається фігура, обмежена графіком невід'ємної і неперервної на відрізку [a,b] функції, віссю Ох і прямими x=а та x=b. Криволінійна трапеція та її площа. Криволінійною трапецією називається фігура, обмежена графіком невід'ємної і неперервної на відрізку [a,b] функції, віссю Ох і прямими x=а та x=b.](/uploads/files/289051/148787/161315_images/5.jpg)





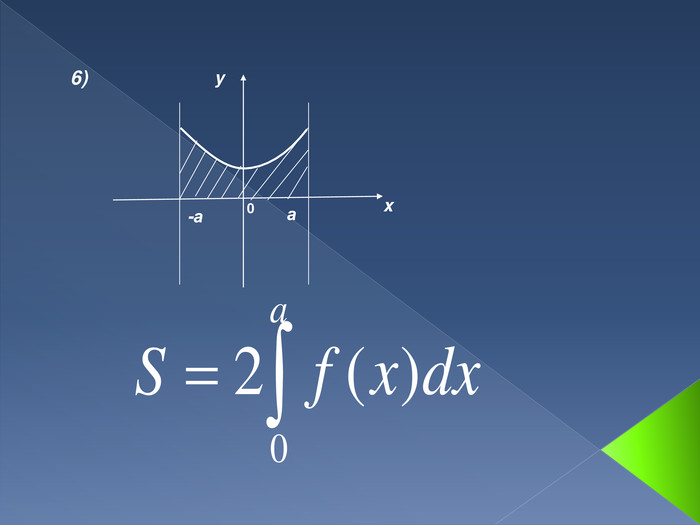
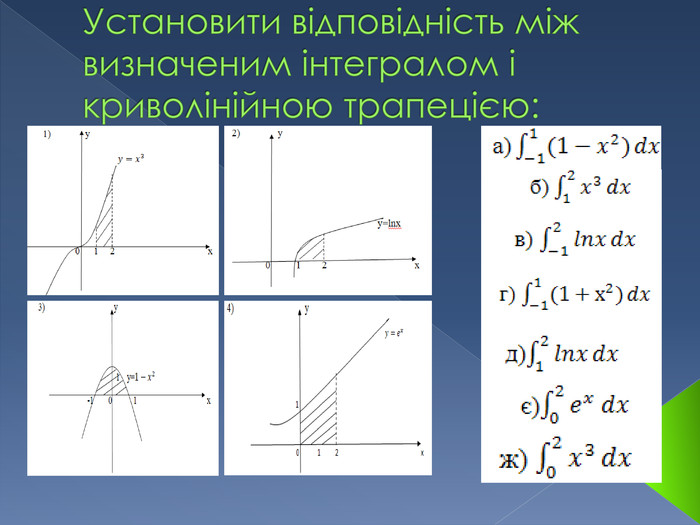
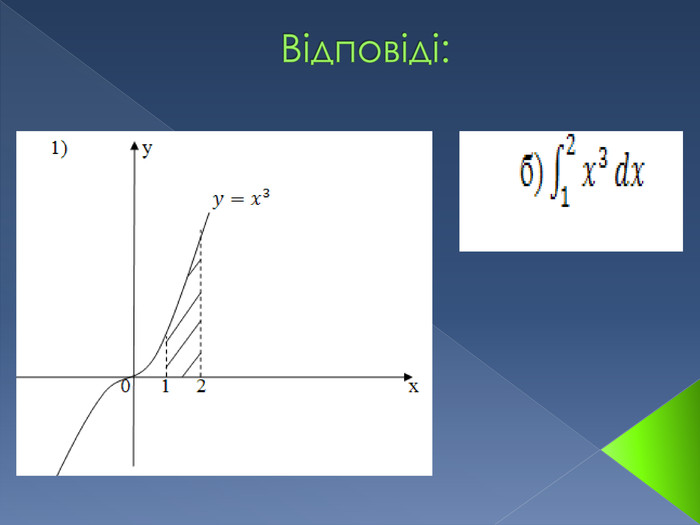
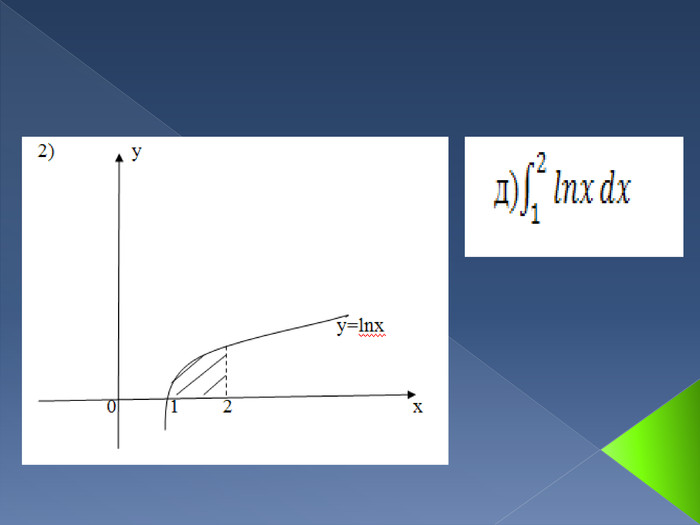
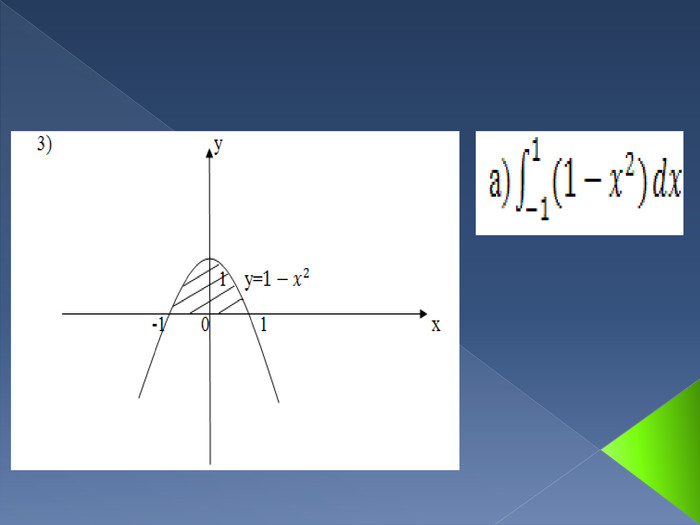
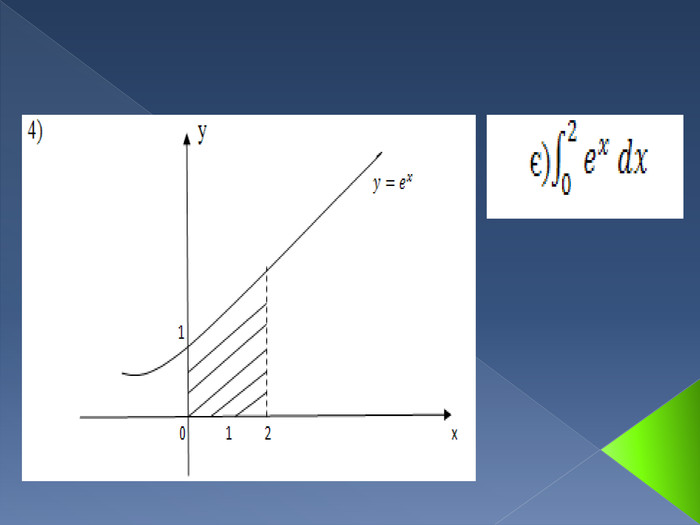





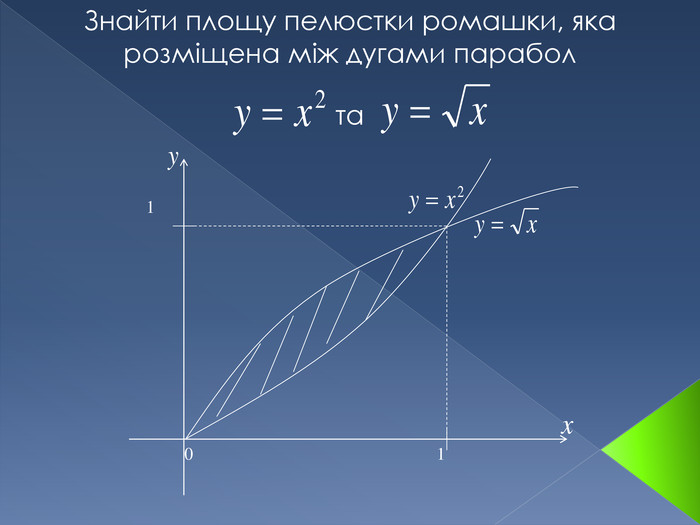














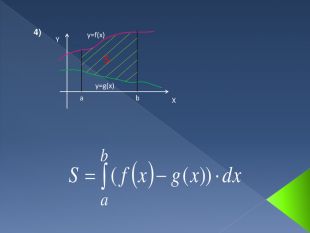
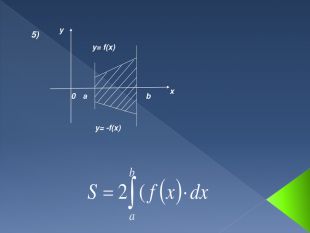
Інтеграл. В математичному аналізі інтегралом функції називають розширення поняття суми. Процес знаходження інтеграла називається інтегруванням. Цей процес зазвичай використовується при знаходженні таких величин як площа, об'єм, маса, зсув, тощо, коли задана швидкість або розподіл змін цієї величини по відношенню до деякої іншої величини (розташування, час тощо).
ІсторіяІнтеграл в давнинуІнтеграція простежується ще в давньому Єгипті, приблизно у 1800 до н.е., Московський математичний папірус демонструє знання формули об'єму січної піраміди. Першим відомим методом для розрахунку інтегралів є метод вичерпання Евдокса (приблизно 370 до н. е.), який намагався знайти площі і об'єми, розриваючи їх на нескінченну безліч частин, для яких площа або об'єм вже відомий. Цей метод був підхоплений і розвинутий Архімедом, і використовувався для розрахунку площ парабол і наближеного розрахунку площі круга. Знак інтеграла (∫), був вперше використаний Лейбніцом в кінці XVII століття. Цей символ утворився з букви ſ («довга s») — скорочення слова лат. ſumma (summa, сума).
На честь Ньютона названо одиницю сили в Міжнародній системі одиниць — Ньютон. Ньютон був першою людиною в Англії, яку висвятили в лицарі за наукові заслуги. Член Паризької Академії Наук з 1699 року. Розробка диференціального обчислення та інтегрального числення стала важливою віхою у розвитку математики. Лейбніц незалежно від Ньютона створив диференціальне й інтегральне числення і заклав основи двійкової системи числення. У рукописах і листуванні, які було надруковано лише в середині 19 ст., розробив основи теорії детермінантів. Лейбніц розпочав дослідження з диференціального й інтегрального числення. Він надавав надзвичайну увагу питанням зручної наукової нотації і в рукописі від 21 листопада 1675 р. він уперше використав нині загальновизнанний запис для інтегралу функції.


про публікацію авторської розробки
Додати розробку