Урок "Визначений інтеграл та його застосування"

Тема. Визначений інтеграл та його застосування

Мета: узагальнити та систематизувати знання учнів з теми «Визначений інтеграл та його застосування»; розвивати логічне мислення учнів; показати значення математики у житті та розвитку різних наук; виховувати бачення цілісності світу.

Обладнання: презентації.

Тип уроку: урок-конференція.

Хід уроку

І. Організаційний етап

1. Вступне слово вчителя, оголошення теми та мети уроку.

2. Історична довідка.

3. Застосування визначеного інтегралу в геометрії:

    1) обчислення площ плоских фігур;

    2) обчислення об’ємів тіл обертання.

4. Застосування визначеного інтегралу у фізиці.

5. Застосування визначеного інтегралу в економіці.

6. Застосування визначеного інтегралу у біології.

7. Застосування визначеного інтегралу у побуті.

8. Підбиття підсумків уроку.

ІІ. Історична довідка (презентація 1-5 слайди)

ІІІ. Застосування визначеного інтегралу в геометрії

1. Обчислення площ плоских фігур – І група

а) Презентація (6-9 слайди)

б) Приклад .

Знайти площу фігури, обмеженої параболою у = 4 – х² та прямими

Розв’язання

На відрізку [-2; 0]

а на відрізку [0; 2]

Шукану площу знаходимо як суму двох інтегралів:

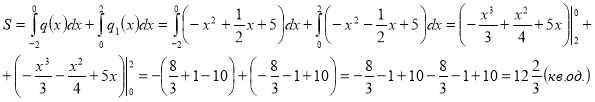
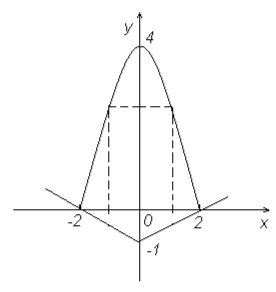
Також площу даної фігури можна обчислити раціонально, якщо звернути увагу на те, що фігура симетрична відносно осі Оу:

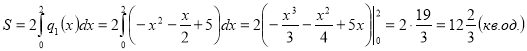
Відповідь: S_ф = кв.од.

2. Обчислення об’ємів тіл – ІІ група

а) Презентація (7-9 слайди)

б) Приклад.

  Знайти об’єм тіла, утвореного обертанням навколо осі Ох фігури, обмеженої синусоїдою і прямими х = 0,

Розв’язання

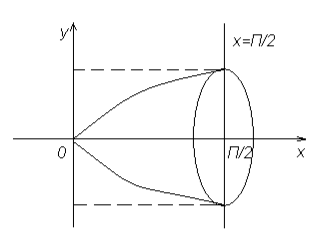
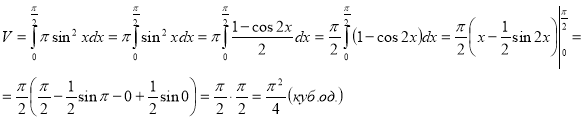
Відповідь:

3. Застосування визначеного інтегралу у фізиці – ІІІ група

а) презентація(15-17)

б) Приклади:

 Обчислення роботи змінної сили

Обчислити роботу, яку треба виконати, щоб викачати воду з ями глибиною 4 м, що має квадратний переріз зі стороною 2 м. Густина води ρ = 10³ кг/м³.

Розв’язання

Спрямуємо вісь Ох вздовж діючої сили. Значення сили F(x), що діє на переріз прямокутного паралелепіпеда площею 4 м², визначається вагою шару води, що знаходиться вище від цього перерізу. Отже,

де м/с.

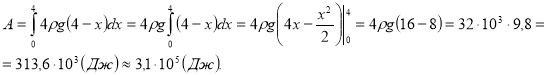
Відповідь: А = 3,1 · 10⁵ Дж.

 Обчислення маси неоднорідного стержня

Знати масу стержня завдовжки 35 см, якщо його лінійна густина змінюється за законом

Розв’язання

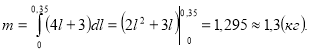
Відповідь: m = 1,3 кг.

 Обчислення кількості електрики

Знайти кількість електрики, що проходить через поперечний переріз провідника за 10 с, якщо сила струму змінюється за законом

Розв’язання

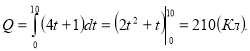
Відповідь: Q = 210 Кл.

4. Застосування визначеного інтегралу в економіці – ІV група

а) презентація(18-21)

б) Приклади:

Експериментально встановлено, що продуктивність праці робітника наближено виражається формулою де t – робочий часу годинах. Обчислити обсяг випуску продукції за квартал, вважаючи робочий день восьмигодинним, а кількість робочих днів у кварталі – 62.

Розв’язання

Обсяг випуску продукції протягом зміни є первісною від функції, що виражає продуктивність праці. Тому 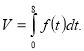Протягом кварталу обсяг випуску продукції становитиме: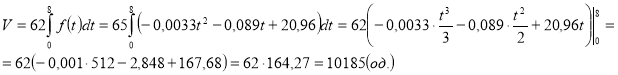

Відповідь: 10 185 (од.)

6 Використання інтеграла в біології – 6 група

a) Презентація(22)

б)Приклад

Середня довжина прольоту.

У деяких дослідженнях необхідно знати середню довжину пробігу, або середню довжину шляху при проходженні тваринам деякого фіксованого ділянки. Наведемо відповідний розрахунок для птахів. Нехай ділянкою буде коло радіуса R. Будемо вважати, що R не дуже велике, так що більшість птахів досліджуваного виду перетинає це коло по прямій.

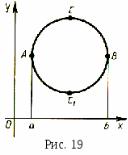Птах може під будь-яким кутом в будь-якій точці перетнути окружність. Залежно від цього довжина її прольоту над колом може бути рівною будь-якій величині від 0 до 2Я (рис. 19). Нас цікавить середня довжина прольоту. Так як коло симетричний щодо будь-якого свого діаметра, нам достатньо обмежитися лише тими птахами, які летять в якомусь одному напрямку, паралельному осі Оу. Тоді середня довжина прольоту - це середня відстань між дугами АСВ. Іншими словами, це середнє значення функції (х) - (х), де у = f (х) - рівняння верхньої дуги, а у = f2 (х) -уравненіе нижньої дуги, т. Е.

L = або L =

Так як рівний площі криволінійної трапеції аАСВb),

дорівнює площі криволінійної трапеції, то їх різниця дорівнює площі кола, т. е. Різниця b - а дорівнює, очевидно, 2R. Підставивши це в L = , отримаємо: L = = R

7 Застосування інтеграла в побуті

а) Презентація(23)

ІV Підсумок уроку

V Домашнє завдання Підготуватися до контрольної роботи.