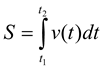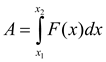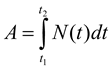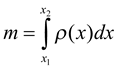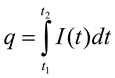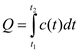Казанківський професійний аграрний ліцей               

Збірка математичних задач з використання інтегрального числення в різних областях

науки

 

Методичний посібник на допомогу вчителю

Укладач вчитель математики 

 Васильєва Л.О.

        

 

 Історія розвитку поняття інтеграла й інтегрального обчислення пов’язана з потребою в обчисленні площ фігур, а також поверхонь і об’ємів довільних тіл. Передісторія інтегрального обчислення сягає глибокої давнини: ідеї інтегрального обчислення можна знайти в роботах давньогрецьких учених Евдокса Кнідського (бл.408-355 до

н.е.) і Архімеда (бл.287-212 до н.е.).​    

                Основні       поняття       та       теорія       інтегрального       і

диференціального числень, перш за все зв'язок операцій диференціювання й інтегрування, а також їх застосування до розв'язання прикладних задач були розроблені в кінці XVII століття, але грунтувалися на ідеях, сформульованих на початку XVII столітті великим математиком і астрономом Иоганном Кеплером.

В листопаді 1613 королівський математик і астролог

австрійського двору І. Кеплер святкував весілля. Готуючись до неї, він придбав кілька бочок виноградного вина. При покупці Кеплер був вражений тим, що продавець визначав місткість бочки, виробляючи одне єдине дію - вимірюючи відстань від наливного отвори до найдальшої від нього точки днища. Адже такий вимір абсолютно не враховувало форму бочки! Кеплер відразу побачив, що перед ним найцікавіша математична задача - по декількох вимірюваннях обчислити місткість бочки. Розмірковуючи над цим завданням, він знайшов формули не тільки для обсягу бочок, але й для об'єму самих різних тіл: лимона, яблука, айви і навіть турецької чалми. Для кожного з тіл Кеплеру доводилося створювати нові, часто дуже хитромудрі методи, що було вкрай незручно. Спроба знайти досить загальні, а, головне, прості методи вирішення

подібних завдань і призвела до виникнення сучасного інтегрального числення. Але це вже була заслуга зовсім

іншого математика.

Всі процеси протікають із певною швидкістю, всі величини, що беруть участь у цих процесах, змінюються, причому у взаємозв’язках. Тому постала необхідність у такому апараті, за допомогою якого можна було б вивчати змінні

процеси.      Саме     таких     апарат     і     був    розроблений     у

математичному аналізі.

                      Дана      збірка      дає      відповідь      на      питання:      «Де

застосовуються інтегральні обчислення?». А також розкриває всю їх важливість та значущість не тільки для математики, але

й для фізики, техніки, економіки та навіть хімії.

 

Застосування інтеграла в фізиці. 

 

 

1. Обчислення пройденого шляху за відомим законом зміни швидкості.

Задача1.​Тіло рухається зі швидкістю, яка змінюється за законом  υ = 2t+1 (м\c). Знайти шлях, який пройшло тіло за проміжок часу від t^​₁ =1_​ c до t^​₂ =3_​ c.

Розв’язання:

3

S = ∫ (2t + 1)dt   = (2 ^t₂² + t) = (9 + 3 – (1+1)) = 10 (м).

1

Задача2.​ Для кращого обслуговування заїзду гонок серії «Формула-1» майстри визначили найкращий закон зміни швидкості руху автомобіля прямою

5 трасою: V=2(t + 2)² . Який шлях:

 а) проїде пілот цієї гонки за 7 с. від початку руху; 

б) він проїде за сьому секунду?

Розв’язання:  

а)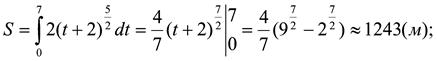  

         б)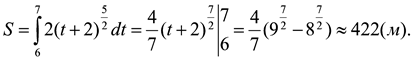  

2. Обчислення маси неоднорідного стержня.

Задача3. ​Знайти масу стрижня 35 см завдовжки, якщо його лінійна густина змінюється за законом  ρ(​l​) = 4​l+ 3 ​(кг/м)

Розв’язання:

m = 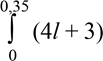dl   = (2​l​^{2 ​}+ 3l​)                   = 1,295≈1,3 (кг). 

 

    ​Задача4.​  Обчисліть масу ділянки стрижня від х^​₁=1_​ до х^​₂=2_​ , якщо його лінійна щільність задається формулою ρ(х)=4х​^3​+5х+2 (г/см).

Розв’язання:  Знаходимо масу ділянки

 

 

 

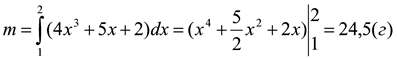
3.   Обчислення кількості електрики. 

Задача5.​  Знайти кількість електрики, про проходить через поперечний переріз провідника за 10 с, якщо сила струму змінюється за законом  I (t) = 4t+1 (A).

 

Розв’язання:  

Ԛ = 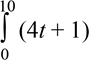dt   = (2​t​^{2 ​}+ t​)        = 210 (Кл). 

 

4.   Обчислення  сили тиску рідини. 

 

Задача6. ​Акваріум має форму прямокутного паралелепіпеда. Знайти силу тиску води (густина води 1000 кг/м​^3​), яка наповнює акваріум, на одну з його вертикальних стінок, розміри якої 0,4 х 0,7 м.

Розв’язання: 

Візьмемо систему координат так, щоб осі ​Оу ​і ​Ох відповідно містила верхню основу і бічну сторону вертикальної стіни акваріума.

Стінка має форму прямокутника, тому .

Оскільки межі інтегрування ​a=0​ i ​b=0,4​, то дістанемо

.

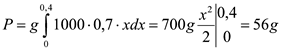Враховуючи, що м/с​^2​ , маємо  

5. Обчислення сили пружності пружини.

Задача7. Сила пружності пружини, розтягнутої на 0,05м, дорівнює 3Н. Яку роботу треба виконати, щоб розтягти пружину на ці 0,05м?

 

 

Розв’язання:  

За законом Гука сила F, яка розтягує        або стискає        пружину, пропорційна цьому розтягу або стиску, тобто , де ​х – величина розтягу або        стиску,    ​k      -       коефіцієнт пропорційності. З умови випливає, що , тобто ​k=60​, отже, ​F=60х​.

Використовуючи формулу (3), дістаємо 

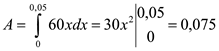(Дж).

 

6. Обчислення  виконаної роботи.

Задача8. ​Обчислити роботу, яку треба виконати, щоб викачати воду з ями глибиною 4 м, що має квадратний переріз зі стороною 2 м. Густина води ρ = 10​^3​ кг/м​^3​. 

Розв’язання:

Спрямуємо вісь Ох вздовж діючої сили. Значення сили F(x), що діє на переріз прямокутного паралелепіпеда площею 4 м​^2​, визначається вагою шару води, що знаходиться вище від цього перерізу. Отже, 

м/с.

 

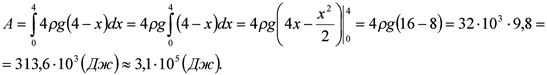
Відповідь: А = 3,1 · 10​^5​ Дж

Задача9.​ Яку потрібно виконати роботу, щоб розтягнути пружину на 3 см, якщо сила в 10 Н розтягує пружину на 1 см? 

Розв’язання:  

Згідно з законом Гука, сила F, що розтягує пружину, пропорційна переміщенню х вільного кінця пружини, тобто

F=kx. Для знаходження коефіцієнта k скористаємось тим, що 

 

сила в 10Н розтягує пружину на 0,01 м: 10=0,01· k, k=1000.

Тоді F=1000х.  Маємо:

 

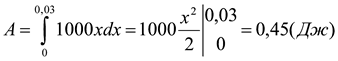
Задача 10​.Сріблення деталі проводять при силі струму, що змінюється за законом І(t)=2t+1. Яка кількість срібла була витрачена за час 120с. Електрохімічний еквівалент срібла k = 1,118 • 10⁻⁶кг/Кл.

Розв’язання:

Згідно закону електролізу маємо: ​m=kq.

Використовуючи технічний зміст інтеграла маємо:

t₂ q = ∫ I (t)dt , де I (t) =2t + 1 , t₁ = 0с, t₂ =120         с.

t₁

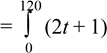
t22 qdt =2 ₂ + t|=t + t|=14400+120-(0+0)=

= 14520-0=14520 (Кл).

m=1,118 • 10⁻⁶ • 14520=0    ,01623336 кг. =16,23336г.

 

 

 

Таблиця фізичних величин та співвідношень між ними.

№ п п	Величини	Співвідношення	Знаходження  похідної	Знаходження  інтеграла
1	S​ – переміщен ня v ​-​- швидкість
2	A​ - робота F​ - сила
3	A ​- робота N - потужніст ь
4	m​– маса тонкого стержня  - лінійна густина
5	q​– електричн ий заряд I​ – сила струму
6	Q​ – кількість теплоти c​- теплоємніс ть

 

 

 

Застосування інтеграла  в  економіці.  

 

Задача11​. Експериментально встановлено, що залежність витрати бензину автомобілем від швидкості на 100 км шляху визначається за формулою 

Ԛ = 18- 0,3 υ + 0,003 υ​^2​,

де 30 ≤ υ ≤ 110. Визначити середню витрату бензину при швидкості руху 50-60 км/год.

Розв’язання:

Середня витрата бензину

m = 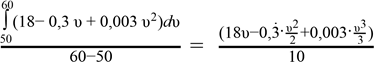  =  (18·60 – 

- 0,3·1800+ 0,003·72000 - 18·50 + 0,3 ·1250 – 0,003·41667) =10,6 (л).

Отже, автомобіль на 100км шляху, рухаючись зі швидкістю 50- 60 км/год, витрачає в середньому 10,6 л бензину. 

 

Задача12​.​ Завод випускав за рік 15 000 верстатів, а потім збільшив їх випуск на 55 верстатів щорічно . Визначити суму амортизаційних відрахувань за 10 років при нормі амортизації 5 %, якщо вартість одного верстата становить 1 745 грн. 

Вказівка. Випуск верстатів можна виразити формулою  V =

15000 +55t, де t  - кількість років.

Розв’язання:

  V = 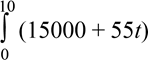dt   = (15000​t​ ^​+ ⁵⁵₂^t2 )    = 150 000 + 2 750 =

152 750 (грн.). 

Від одержаної суми знаходимо 5 %, що становитиме 7637,5 грн. 

 

Задача13.​ Чисті інвестиції задано функцією .

Визначити:

а) приріст капіталу за три роки;

б) термін часу (у роках), після якого приріст капіталу складає 50000.

Розв’язання: 

а) Скористаємося формулою для обчислення , поклавши

                                                                           поклавши =0;      =3.

.

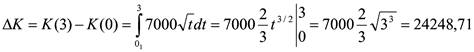б) Позначимо шукану тривалість часу через Т, тоді 

.

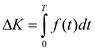Підставляємо .

 

 

 

 

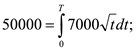
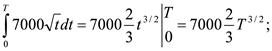
                      Задача14.        Експериментально        встановлено,        що

продуктивність       праці робітника      наближено    виражається

функцією:

f​(​t​) = -0,0033​t​^2​ – 0,089​t​ + 20,96,

де ​t – робітничий час у годинах. Обчислити обсяг випуску продукції за квартал, вважаючи робочий день

восьмигодинним, а кількість робочих днів у кварталі 62.

Розв’язання:

Обсяг випуску продукції протягом зміни є первісною від

функції, що виражає продуктивність праці. Тому

.

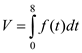Протягом кварталу обсяг випуску продукції становитиме:

 

 

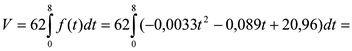
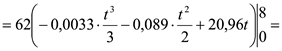
(од.).

Задача15. На  полі   пшениці  після   приземлення космічного корабля  залишився  слід,    який   нагадує    

фігуру,     обмежену    лініями   у =​│х2 – 2х - 8│ та  у = 3 + │х - 1│. Необхідно визначити

збитки, завдані агрокомплексом, якщо з 1 м2 отримують в

середньому 3,8 кг пшениці, яка коштує  0,8 грн. / кг.

Розв’язання:

 

 

 

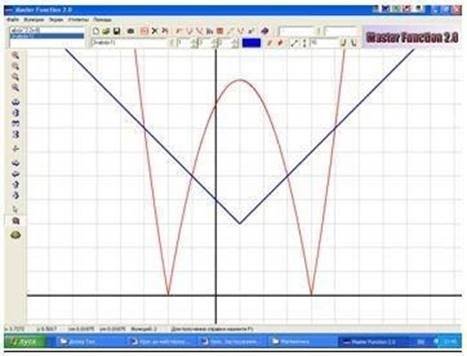
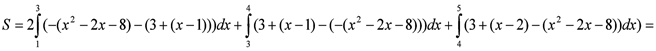
=2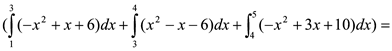26 ₃² (м²​^​)

В= 26 ₃² ·3,8·0,8 = 81,07 (грн.).

 

 

Застосування інтеграла в

хімії.  

 

 

Задача16. Швидкість зміни концентрації речовини, що

вступила в реакцію, виражається функцією ​v = 3​t + 1, де ​t – час (с), ​v – швидкість (моль/см​^3​). Як зміниться концентрація

речовини за час t^​₁=0_​ до t^​₂ =5 c?_​

Розв’язання:

Оскільки ​v​(​t​)=​C​`(​t​) ,то ​C​(​t​) – концентрація речовини і

первісна для ​v​(​t​), тому

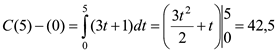 (моль/м​^3​).

 

Застосування інтеграла в математиці  

 

 

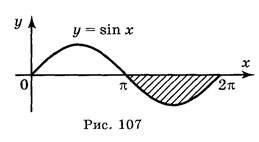
Приклад 1.​ ​Обчислити площу фігури, обмеженої лініями ​у

=​ sin ​x, у ​= 0,            π < ​x < ​2π.

Розв'язання:

Побудуємо фігуру, площу якої треба обчислити (рис. 107). На заданому проміжку функція ​у =​ sin ​x​  0. Тому обчислення площі цієї фігури

замінимо       обчисленням площі      криволінійної        трапеції, симетричної даній фігурі відносно осі абсцис, тобто обмеженої графіком функції ​у = - sin x​ і віссю абсцис.

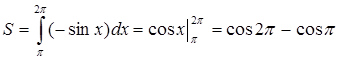= 1 + 1 = 2.

 

Приклад2.​ ​Обчисліть        площу    фігури,   обмеженої лініями: ​у​ = ​x​^{2 ​}і ​у​ = ​-x + 2.

Розв'язання:

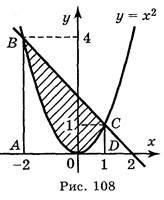Зобразимо схематично графіки даних функцій (рис. 108). Бачимо, що шукана площа є різницею площ двох криволінійних трапецій:

S = S​ABCD​ ​–​ S​ABOCD​.

З рисунка видно, що межі інтегрування для обох трапецій одні і ті самі, це абсциси

спільних точок графіків даних функцій. Для знаходження меж інтегрування розв'яжемо рівняння: x​^2​ = ​-x +​ 2; ​x​^2​ + x - 2​ =​ ​0; ​x^​_1​ = -2, ​x^​_2​ = 1.

Знайдемо шукану площу:

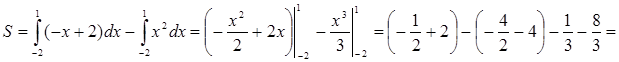
   = ​1,5 + 6 – 3 = 4,5.

 ​Приклад          3. ​Знайдіть        площу      фігури,      обмеженої

параболами ​у = х​^{2 ​}і ​у = 2х - х​^2​ та віссю ​ОХ.

 

 

Розв'язання:

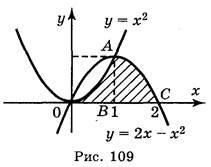
Побудуємо графіки функцій ​у​ = ​х​^{2 ​}і у​ = ​2х - х​^2​ і знайдемо абсциси точок перетину цих графіків із рівняння: ​х​^2​ = 2​х​ – ​х​^2​. Корені цього рівняння ​х^​₁ =_​ ​ 0, ​х^​₂ =_​ 1. Дана фігура зображена на рис. 109.

Із рисунка видно, що ця фігура складається з двох криволінійних трапецій: ​ОАВ​ і ​ВАС.

Отже, шукана площа дорівнює сумі площ цих трапецій:

 

 

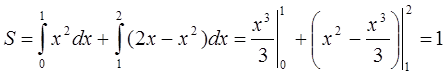
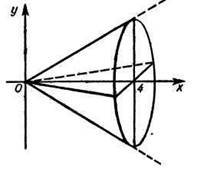
Приклад 4. ​Нехай фігура, обмежена прямими , х=4 і віссю ​Ох​, обертається навколо осі ​Ох​. Одержане тіло обертання – конус. Знайти його об’єм.

 

Розв’язання:

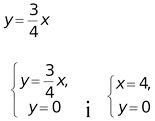Межами інтегрування являються абсциси точок перетину прямих  і ​х=​4 з віссю ​Ох​. Знаходимо

системи          Отже,  Далі знаходимо 

 

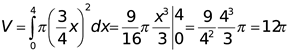
Розв’яжемо цю задачу за допомогою формули знаходження об’єму кругового конуса. Маємо .

Знаходимо радіус основи. З рівняння  при ​х=​4 → ​R=​3

Висота конуса ​h=​4. Таким чином,

 

 

 

 

 

 

 

 

 

 

 

 

Використана література

 

1.   Навчальний посібник «Алгебра і початки аналізу»\\

\\М.І. Шкіль, З.І. Слєпкань, 2000 р.

2.   http://shkola.ostriv.in.ua

3.   https://fizmat.7mile.net

4.   https://www.schoolua.com