Завдання для І етапу Всеукраїнської олімпіади з математики "Шкільні олімпіади з математики. 5-11 клас"
Варіанти завдань для I етапу (шкільних) Всеукраїнських олімпіад школярів з математики в 5-11 класах. Набір завдань можна брати будь-який, як і бали до них. Все залежить від часу, який у вас є і класу з яким працюєте.
|
Олімпіада з математики. I етап. 5 клас. 1. Барвінок виростив у своєму саду 246 кг яблук і 354 кг груш. Шосту частину всіх фруктів Барвінок віддав своїм друзям з дитячого садочка, п'яту частину всіх фруктів - друзям зі школи, а решта - в лікарню. Скільки кілограмів фруктів віддав Барвінок в лікарню? (10б.) 2. У записі 4 4 4 4 4 4 4 4 поставте між деякими цифрами знак «+» так, щоб вийшло вираз, значення якого дорівнює 500. (15б.) 3. Попелюшка отримала від мачухи два відра, одне ємністю в 7 л, інше в 5 л. Мачуха відправила її до джерела з вимогою принести рівно 2 л води. Як може виконати це завдання Попелюшка? (15б) 4. У двох кімнатах було 76 осіб. Коли з однієї кімнати вийшли 30, а з другої 40, то людей залишилося порівну. Скільки людей було в кожній кімнаті спочатку ? (15 б) 5. Троє друзів: Альоша, Боря і Вітя - вчаться в одному класі. Один з них їздить додому зі школи на автобусі, один - на трамваї і один на тролейбусі. Одного разу після уроків Альоша пішов проводити свого друга до зупинки автобуса. Коли повз них проходив тролейбус, третій друг крикнув з вікна: «Боря, ти забув в школі зошит!». Хто на чому їздить додому? (20 б.) 6. З сірників складено невірна рівність. Перекладіть один сірник так, щоб вийшло вірна рівність. (20 б.)
(20 б.)
|
Олімпіада з математики. I етап. 5 клас. 1. Барвінок виростив у своєму саду 246 кг яблук і 354 кг груш. Шосту частину всіх фруктів Барвінок віддав своїм друзям з дитячого садочка, п'яту частину всіх фруктів - друзям зі школи, а решта - в лікарню. Скільки кілограмів фруктів віддав Барвінок в лікарню? (10б.) 2. У записі 4 4 4 4 4 4 4 4 поставте між деякими цифрами знак «+» так, щоб вийшло вираз, значення якого дорівнює 500. (15б.) 3. Попелюшка отримала від мачухи два відра, одне ємністю в 7 л, інше в 5 л. Мачуха відправила її до джерела з вимогою принести рівно 2 л води. Як може виконати це завдання Попелюшка? (15б) 4. У двох кімнатах було 76 осіб. Коли з однієї кімнати вийшли 30, а з другої 40, то людей залишилося порівну. Скільки людей було в кожній кімнаті спочатку ? (15 б) 5. Троє друзів: Альоша, Боря і Вітя - вчаться в одному класі. Один з них їздить додому зі школи на автобусі, один - на трамваї і один на тролейбусі. Одного разу після уроків Альоша пішов проводити свого друга до зупинки автобуса. Коли повз них проходив тролейбус, третій друг крикнув з вікна: «Боря, ти забув в школі зошит!». Хто на чому їздить додому? (20 б.)
7. У квадратній кімнаті треба розставити уздовж стін 10 стільців так, щоб у кожної стіни стояло порівну стільців. Як це зробити? (20 б.)
|
![]() Олімпіада з математики. I етап. 6 клас.
Олімпіада з математики. I етап. 6 клас.
1. Якийсь товар коштував 500гривен. Потім ціну на нього збільшили на 10%, а потім зменшили на 10%. Який стала ціна в підсумку? (15б)
2. Які цифри можна підставити замість зірочки в запис
тризначного числа 46 *, щоб вийшло число, яке б ділилося
на : а) 2; б) на 3; в) на 5. (15б)
3.Площа прямокутника 576 см2, ширина його 18 см. Знайдіть площу такого квадрату, у якого периметр дорівнює периметру прямокутника. (20б)
4. Довести, що сума двох послідовних непарних чисел
ділиться без остачі на 4. (20б)
5. Чи можна в квадраті 4 × 4 розставити 10 мінусів так, щоб
в кожному рядку було парне число мінусів, а в кожному
стовпці – непарне? (20б)
6. Для влаштування ялинки купили цукерок, горіхів і пряників.
Причому горіхів взяли на 80 штук більше, ніж цукерок, а
пряників на 120 менше, ніж горіхів. Яке найбільше число
однакових подарунків для дітей можна зробити, якщо всього
цукерок, горіхів і пряників 760 штук?(30б)
7. Вздовж паркану ростуть 8 кущів малини. Число ягід на сусідніх кущах відрізняється на 1. Чи може на всіх кущах разом бути 225 ягід? (30б)
Олімпіада з математики. I етап. 6 клас.
1. Якийсь товар коштував 500гривен. Потім ціну на нього збільшили на 10%, а потім зменшили на 10%. Який стала ціна в підсумку? (15б)
2. Які цифри можна підставити замість зірочки в запис
тризначного числа 46 *, щоб вийшло число, яке б ділилося на : а) 2; б) на 3; в) на 5. (15б)
3.Площа прямокутника 576 см2, ширина його 18 см. Знайдіть площу такого квадрату, у якого периметр дорівнює периметру прямокутника. (20б)
4. Довести, що сума двох послідовних непарних чисел
ділиться без остачі на 4. (20б)
5. Чи можна в квадраті 4 × 4 розставити 10 мінусів так, щоб в кожному рядку було парне число мінусів, а в кожному стовпці – непарне? (20б)
6. Для влаштування ялинки купили цукерок, горіхів і пряників. Причому горіхів взяли на 80 штук більше, ніж цукерок, а пряників на 120 менше, ніж горіхів. Яке найбільше число однакових подарунків для дітей можна зробити, якщо всього цукерок, горіхів і пряників 760 штук?(30б)
7. Вздовж паркану ростуть 8 кущів малини. Число ягід на сусідніх кущах відрізняється на 1. Чи може на всіх кущах разом бути 225 ягід? (30б)
![]() Олімпіада з математики. I етап. 7 клас.
Олімпіада з математики. I етап. 7 клас.
1. Розв’яжіть рівняння: а![]() ;
;
б) ![]() + 0,3
+ 0,3![]() (20 б)
(20 б)
2.Знайдіть цілі числа ![]() і
і ![]() такі, що
такі, що ![]() . (20 б)
. (20 б)
3.Сума двох чисел дорівнює 77. Добуток одного з них на 8 дорівнює добутку іншого на 6. Знайдіть найбільше з цих чисел. (15 б)
4. Влітку ціну на лижі знизили на 10%, а взимку підняли
на 10%. Чи змінилася ціна на лижі і на скільки відсотків?
(20 б)
5. Велика група туристів виїхала в закордонне турне. З них володіє англійською мовою 28 осіб, французькою - 13, німецькою - 10, англійською та французькою - 8, французькою та німецькою - 5, англійською та німецькою - 6, всіма трьома мовами - двоє, а 41 людина не володіє жодною з трьох мов. Скільки всього туристів? (20 б)
6. Фігури 1,2,3,4,5 - квадрати. Периметр квадрата 1 дорівнює
8 м. Знайдіть периметр квадрата 5 (див. рис 1).
рис.1 (20 б)
7. Розмістіть 6 точок на чотирьох прямих так, щоб на кожній з них було по три точки. (30 б)
Олімпіада з математики. I етап. 7 клас.
1. Розв’яжіть рівняння: а![]() ;
;
б) ![]() + 0,3
+ 0,3![]() (20 б)
(20 б)
2.Знайдіть цілі числа ![]() і
і ![]() такі, що
такі, що ![]() . (20 б)
. (20 б)
3.Сума двох чисел дорівнює 77. Добуток одного з них на 8 дорівнює добутку іншого на 6. Знайдіть найбільше з цих чисел. (15 б)
4. Влітку ціну на лижі знизили на 10%, а взимку підняли
на 10%. Чи змінилася ціна на лижі і на скільки відсотків?
(20 б)
5. Велика група туристів виїхала в закордонне турне. З них володіє англійською мовою 28 осіб, французькою - 13, німецькою - 10, англійською та французькою - 8, французькою та німецькою - 5, англійською та німецькою - 6, всіма трьома мовами - двоє, а 41 людина не володіє жодною з трьох мов. Скільки всього туристів? (20 б)
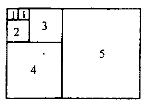 6. Фігури 1,2,3,4,5 - квадрати. Периметр квадрата 1дорівнює
6. Фігури 1,2,3,4,5 - квадрати. Периметр квадрата 1дорівнює
8 м. Знайдіть периметр квадрата 5 (див. рис 1).

рис.1 (20 б)
7. Розмістіть 6 точок на чотирьох прямих так, щоб на кожній з них було по три точки. (30 б)
![]() Олімпіада з математики. I етап. 8 клас.
Олімпіада з математики. I етап. 8 клас.
1.Знайдіть значення виразу ![]() , якщо
, якщо ![]()
![]()
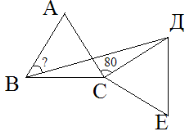
2. Два однакових рівносторонніх трикутника АВС і СДЕ мають спільну вершину С. Знайдіть
∠ АВД, якщо ∠АСД = 80 °. (15б)
3. Розв’яжіть рівняння:
![]() (20б)
(20б)
4. Через п'ять років вік брата буде відноситися до віку сестри як
8: 7. Скільки років кожному з них зараз, якщо рік тому брат
був удвічі старший за сестру? (20б)
5. У магазині побувало 65 осіб. Відомо, що вони купили 35 холодильників, 36 мікрохвильовок, 37 телевізорів. 20 з них купили і холодильник, і мікрохвильовку, 19 - і мікрохвильовку, і телевізор, 15-холодильник і телевізор, а все три покупки зробили три людини. Чи був серед них відвідувач, що не купив нічого? (20б)
6. У трикутнику АВС бісектриса, яка проведена з вершини А, висота - з вершини В і серединний перпендикуляр до сторони АВ, перетинаються в одній точці. Знайдіть величину кута А. (20б)
7. Розкладіть на множники вираз: ![]() (20б)
(20б)
8. Докажіть, що коли ![]() (20б)
(20б)
Олімпіада з математики. I етап. 8 клас.
1.Знайдіть значення виразу ![]() , якщо
, якщо ![]()
![]()
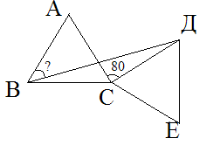
2. Два однакових рівносторонніх трикутника АВС і СДЕ мають спільну вершину С. Знайдіть
∠ АВД, якщо ∠АСД = 80 °. (15б)
3. Розв’яжіть рівняння:
![]() (20б)
(20б)
4. Через п'ять років вік брата буде відноситися до віку сестри як
8: 7. Скільки років кожному з них зараз, якщо рік тому брат
був удвічі старший за сестру? (20б)
5. У магазині побувало 65 осіб. Відомо, що вони купили 35 холодильників, 36 мікрохвильовок, 37 телевізорів. 20 з них купили і холодильник, і мікрохвильовку, 19 - і мікрохвильовку, і телевізор, 15-холодильник і телевізор, а все три покупки зробили три людини. Чи був серед них відвідувач, що не купив нічого? (20б)
6. У трикутнику АВС бісектриса, яка проведена з вершини А, висота - з вершини В і серединний перпендикуляр до сторони АВ, перетинаються в одній точці. Знайдіть величину кута А. (20б)
7. Розкладіть на множники вираз: ![]() (20б)
(20б)
8. Докажіть, що коли ![]() (20б)
(20б)
![]() Олімпіада з математики. I етап. 9клас.
Олімпіада з математики. I етап. 9клас.
1.Знайдіть область визначення функції:
![]()
2. Доведіть, що ![]() при всіх дійсних значеннях x і y. (10б)
при всіх дійсних значеннях x і y. (10б)
3. Доведіть, що ![]() якщо
якщо![]()
4. Довести, що сума трьох послідовних степенів числа 2 ділиться на 7. (10б)
5. Число одиниць двозначного числа на 3 менше числа десятків. Добуток цього числа на число, записане в зворотному порядку дорівнює 574. Знайти це число. (10б)
6. Розв’яжіть рівняння:
![]()
б)![]()
7. Бічна сторона рівнобедреного трикутника дорівнює 8 см, а медіана, яка проведена до неї, - 6см. Знайдіть основу трикутника. (10б)
8. У трикутнику АВС бісектриса, яка проведена з вершини А, висота з вершини В і серединний перпендикуляр до сторони АВ перетинаються в одній точці. Знайдіть величину кута А. (10б)
9. Доведіть, що з рівності ![]() , де
, де![]()
![]()
![]()
![]() (20б)
(20б)
Олімпіада з математики. I етап. 9клас.
- Знайдіть область визначення функції:
![]()
2. Доведіть, що ![]() при всіх дійсних значеннях x і y. (10б)
при всіх дійсних значеннях x і y. (10б)
3. Доведіть, що ![]() якщо
якщо![]()
4. Довести, що сума трьох послідовних степенів числа 2 ділиться на 7. (10б)
5. Число одиниць двозначного числа на 3 менше числа десятків. Добуток цього числа на число, записане в зворотному порядку дорівнює 574. Знайти це число. (10б)
6. Розв’яжіть рівняння:
![]()
б)![]()
7. Бічна сторона рівнобедреного трикутника дорівнює 8 см, а медіана, яка проведена до неї, - 6см. Знайдіть основу трикутника. (10б)
8. У трикутнику АВС бісектриса, яка проведена з вершини А, висота з вершини В і серединний перпендикуляр до сторони АВ перетинаються в одній точці. Знайдіть величину кута А. (10б)
9. Доведіть, що з рівності ![]() , де
, де![]()
![]()
10. Для кожного значення ![]()
![]() (20б)
(20б)
![]() Олімпіада з математики. I етап. 10 клас
Олімпіада з математики. I етап. 10 клас
1.(15б) Скільки розв’язків має система рівнянь:
![]()
2.(15б) Нехай ![]() і
і ![]() – корні рівняння
– корні рівняння ![]() . Використовуючи теорему Вієта встановіть, правильною або неправильною дробом є значення дробу:
. Використовуючи теорему Вієта встановіть, правильною або неправильною дробом є значення дробу:
![]()
3.(15б) Знайдіть область визначення функції:
![]()
4. (15б) Спростіть: ![]() .
.
5.(15б) На гіпотенузі АВ прямокутного трикутника АВС відзначені точки М і N такі, що AC = AM і BC = BN. Доведіть, що ∠ MCN дорівнює 45 °.
6.( 15б) Розв’яжіть рівняння : ![]()
7. (15б) Перпендикуляр, який опущено з точки окружності на її діаметр, ділить його на два відрізка, один з яких на 27 см більше іншого. Знайдіть довжину кола, якщо довжина даного перпендикуляру дорівнює 18 см.
8.(15б) Відстань між центрами двох кіл, радіуси яких 17 см і 10 см, дорівнює 21 см. Визначити відстань центрів від точки, в якій пряма центрів перетинається із загальною дотичній двох кіл.
9.(20б) Розв’яжіть систему рівнянь: 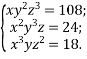
Олімпіада з математики. I етап. 10 клас
1.(15б) Скільки розв’язків має система рівнянь:
![]()
2.(15б) Нехай ![]() і
і ![]() – корні рівняння
– корні рівняння ![]() . Використовуючи теорему Вієта встановіть, правильною або неправильною дробом є значення дробу:
. Використовуючи теорему Вієта встановіть, правильною або неправильною дробом є значення дробу:
![]()
3.(15б) Знайдіть область визначення функції:
![]()
4. (15б) Спростіть: ![]() .
.
5.(15б) На гіпотенузі АВ прямокутного трикутника АВС відзначені точки М і N такі, що AC = AM і BC = BN. Доведіть, що ∠ MCN дорівнює 45 °.
6.( 15б) Розв’яжіть рівняння : ![]()
7. (15б) Перпендикуляр, який опущено з точки окружності на її діаметр, ділить його на два відрізка, один з яких на 27 см більше іншого. Знайдіть довжину кола, якщо довжина даного перпендикуляру дорівнює 18 см.
8.(15б) Відстань між центрами двох кіл, радіуси яких 17 см і 10 см, дорівнює 21 см. Визначити відстань центрів від точки, в якій пряма центрів перетинається із загальною дотичній двох кіл.
9.(20б) Розв’яжіть систему рівнянь: 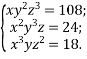
Олімпіада з математики. I етап. 11 клас.
1. Розв'яжіть рівняння: (![]() .
.
2. Розв'яжіть рівняння:![]()
3.![]()
Довжина якої с. Визначте сторони трикутника, що
лежать проти кутів α і β.
4. Розв'яжіть рівняння: lg6 + x lg5= x + lg (2x+1).
5. Розв'яжіть нерівність: ![]()
6. Поясніть детально, в чому помилка доказу:
Беремо вірну нерівність ![]() . З неї випливає, що
. З неї випливає, що
![]() . В силу зростання функції
. В силу зростання функції ![]() ,
,
![]() , звідси
, звідси ![]() . Після скорочення на
. Після скорочення на
![]() , отримуємо
, отримуємо ![]()
7 . Троє друзів, назвемо їх А, В і С, обговорювали питання про можливості одруження. З'ясувалося, що якщо В не буде одружуватися, то і А чи не буде одружуватися, але якщо В одружується, то одружуються і А, і С. Питається, якщо А одружується, то чи повинен при цих умовах одружитися і С?
8. При якому значенні а сума квадратів коренів
рівняння ![]() буде найменшою?
буде найменшою?
9. Функція має вид![]() ,
,![]()
Відомо що ![]() Чому дорівнює
Чому дорівнює
![]()
Всі завдання по 10 балів
![]() Олімпіада з математики. I етап. 11 клас.
Олімпіада з математики. I етап. 11 клас.
1. Розв'яжіть рівняння: (![]() .
.
2. Розв'яжіть рівняння:![]()
3.![]()
Довжина якої с. Визначте сторони трикутника, що
лежать проти кутів α і β.
4. Розв'яжіть рівняння: lg6 + x lg5= x + lg (2x+1).
5. Розв'яжіть нерівність: ![]()
6. Поясніть детально, в чому помилка доказу:
Беремо вірну нерівність ![]() . З неї випливає, що
. З неї випливає, що
![]() . В силу зростання функції
. В силу зростання функції ![]() ,
,
![]() , звідси
, звідси ![]() . Після скорочення на
. Після скорочення на
![]() , отримуємо
, отримуємо ![]()
7 . Троє друзів, назвемо їх А, В і С, обговорювали питання про можливості одруження. З'ясувалося, що якщо В не буде одружуватися, то і А чи не буде одружуватися, але якщо В одружується, то одружуються і А, і С. Питається, якщо А одружується, то чи повинен при цих умовах одружитися і С?
8. При якому значенні а сума квадратів коренів
рівняння ![]() буде найменшою?
буде найменшою?
9. Функція має вид![]() ,
,![]()
Відомо що ![]() Чому дорівнює
Чому дорівнює
![]()
Всі завдання по 10 балів


про публікацію авторської розробки
Додати розробку

-

Пінчук Ірина
13.11.2023 в 21:10
Загальна:
5.0
Структурованість
5.0
Оригінальність викладу
5.0
Відповідність темі
5.0
-

Захарчук Людмила
09.10.2023 в 06:43
ДЯКУЮ ! ЗИЧУ ЗДОРОВЯ, УСПІХІВ У РОБОТІ ,СІМЕЙНОГО ЩАСТЯ .
Загальна:
5.0
Структурованість
5.0
Оригінальність викладу
5.0
Відповідність темі
5.0
-

Шульга Людмила Леонідівна
05.11.2022 в 20:57
Загальна:
5.0
Структурованість
5.0
Оригінальність викладу
5.0
Відповідність темі
5.0
-

Шмагун Наталія
28.10.2022 в 20:19
Дякую!
Загальна:
5.0
Структурованість
5.0
Оригінальність викладу
5.0
Відповідність темі
5.0
-

Федоренко Наталя
19.10.2022 в 20:48
Дякую.
Загальна:
5.0
Структурованість
5.0
Оригінальність викладу
5.0
Відповідність темі
5.0
-

Джежела Людмила
06.10.2022 в 06:54
Загальна:
5.0
Структурованість
5.0
Оригінальність викладу
5.0
Відповідність темі
5.0
-

Доліч Наталія
09.10.2021 в 23:39
Загальна:
4.3
Структурованість
5.0
Оригінальність викладу
4.0
Відповідність темі
4.0
-

Решетняк Вера
08.10.2019 в 22:24
Загальна:
4.0
Структурованість
4.0
Оригінальність викладу
4.0
Відповідність темі
4.0
Показати ще 5 відгуків